卷积、频域乘积和矩阵向量乘积三种形式之间的等价关系与转换
线性移不变系统
线性移不变系统(Linear Time-Invariant System, LTI系统)同时满足线性和时不变性两个条件。
-
线性:如果输入信号的加权和通过系统后,输出是这些输入信号单独通过系统后的输出的相同加权和,那么该系统就是线性的。数学上,对于任意输入信号 x 1 ( t ) x_1(t) x1(t)和 x 2 ( t ) x_2(t) x2(t),以及任意常数 a a a和 b b b,如果系统满足:
y ( t ) = a ⋅ h ( x 1 ( t ) ) + b ⋅ h ( x 2 ( t ) ) y(t) = a \cdot h(x_1(t)) + b \cdot h(x_2(t)) y(t)=a⋅h(x1(t))+b⋅h(x2(t))
其中 h ( ⋅ ) h(\cdot) h(⋅)表示系统对输入的响应,则该系统是线性的。 -
时不变性:如果一个系统的输入信号延迟一段时间后,其输出仅仅是原输出信号同样延迟的时间,而没有其他变化,那么该系统就是时不变的。即,对于任意输入信号 x ( t ) x(t) x(t)及其延迟版本 x ( t − τ ) x(t - \tau) x(t−τ),系统的输出也仅仅是 y ( t ) y(t) y(t)延迟了 τ \tau τ时间单位的版本 y ( t − τ ) y(t - \tau) y(t−τ)。
LTI系统的一个重要性质是,它们可以通过卷积来描述。具体来说,如果 h ( t ) h(t) h(t)是系统的冲激响应(即当输入为单位脉冲时系统的输出), x ( t ) x(t) x(t)是系统的输入信号,那么系统的输出 y ( t ) y(t) y(t)可以通过输入信号与冲激响应的卷积来计算:
y ( t ) = ( x ∗ h ) ( t ) = ∫ − ∞ ∞ x ( τ ) h ( t − τ ) d τ y(t) = (x * h)(t) = \int_{-\infty}^{\infty} x(\tau) h(t - \tau) d\tau y(t)=(x∗h)(t)=∫−∞∞x(τ)h(t−τ)dτ
这个卷积公式表示,LTI系统的输出是输入信号与系统冲激响应之间的一种加权平均。这一性质使得LTI系统在理论分析和实际应用中都变得极其重要,尤其是在滤波器设计、通信系统、图像处理等领域。通过理解系统的冲激响应,可以预测系统对任何输入信号的响应。
卷积还可以写成频域乘积和矩阵向量乘积两种形式。

三者之间的等价关系与转换
时域卷积到频域乘积
①→②和②→①根据卷积定理,时域中的卷积对应于频域中的乘积。时域卷积通常用于理论分析,而频域乘积则更常用于实际计算,尤其是当信号长度较长时,通过快速傅里叶变换(FFT)实现的频域乘积可以显著提高计算效率。
- 傅里叶变换:首先对输入信号 x ( t ) x(t) x(t)和冲激响应 h ( t ) h(t) h(t)进行傅里叶变换,得到它们的频域表示 X ( f ) X(f) X(f)和 H ( f ) H(f) H(f)。
X ( f ) = F { x ( t ) } X(f) = \mathcal{F}\{x(t)\} X(f)=F{x(t)}
H ( f ) = F { h ( t ) } H(f) = \mathcal{F}\{h(t)\} H(f)=F{h(t)}
这里是psf2otf,解释见这里。 - 频域乘积:在频域中,将 X ( f ) X(f) X(f)和 H ( f ) H(f) H(f)相乘,得到输出信号的频域表示 Y ( f ) Y(f) Y(f)。
Y ( f ) = X ( f ) H ( f ) Y(f) = X(f) H(f) Y(f)=X(f)H(f) - 逆傅里叶变换:对 Y ( f ) Y(f) Y(f)进行逆傅里叶变换,得到输出信号 y ( t ) y(t) y(t)。
y ( t ) = F − 1 { Y ( f ) } y(t) = \mathcal{F}^{-1}\{Y(f)\} y(t)=F−1{Y(f)}


时域卷积到矩阵向量乘积
①→③对于有限长的离散信号,卷积可以完全等价地用矩阵向量乘积来表示。这种方法在实现离散信号处理算法时非常有用,它可以利用线性代数来进行表示和计算。
- 构建卷积矩阵:根据冲激响应 h [ n ] h[n] h[n],构建卷积矩阵 H \mathbf{H} H。假设 x [ n ] x[n] x[n]的长度为 N N N, h [ n ] h[n] h[n]的长度为 M M M,则 H \mathbf{H} H是一个 ( N + M − 1 ) × N (N+M-1) \times N (N+M−1)×N的矩阵。
H = [ h [ 0 ] 0 ⋯ 0 h [ 1 ] h [ 0 ] ⋯ 0 ⋮ ⋮ ⋱ ⋮ h [ M − 1 ] h [ M − 2 ] ⋯ h [ 0 ] 0 h [ M − 1 ] ⋯ h [ 1 ] ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ h [ M − 1 ] ] \mathbf{H} = \begin{bmatrix} h[0] & 0 & \cdots & 0 \\ h[1] & h[0] & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ h[M-1] & h[M-2] & \cdots & h[0] \\ 0 & h[M-1] & \cdots & h[1] \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & h[M-1] \end{bmatrix} H= h[0]h[1]⋮h[M−1]0⋮00h[0]⋮h[M−2]h[M−1]⋮0⋯⋯⋱⋯⋯⋱⋯00⋮h[0]h[1]⋮h[M−1] - 矩阵向量乘积:将输入信号 x [ n ] x[n] x[n]表示为列向量 x \mathbf{x} x,计算输出向量 y \mathbf{y} y。
y = H x \mathbf{y} = \mathbf{H} \mathbf{x} y=Hx




矩阵向量乘积到时域卷积
③→①对于一个 n × n n \times n n×n的循环矩阵 C C C和一个 n n n维向量 x x x,计算 C x Cx Cx的过程实际上是一个卷积操作。设 c c c为 C C C的第一列,那么 C x Cx Cx等价于将 c c c和 x x x进行循环卷积。
- 提取冲激响应:从卷积矩阵 H \mathbf{H} H中提取冲激响应 h [ n ] h[n] h[n]。通常, H \mathbf{H} H的第一行或第一列就是 h [ n ] h[n] h[n]。
- 计算卷积:使用提取的 h [ n ] h[n] h[n]和输入信号 x [ n ] x[n] x[n]计算卷积。
y [ n ] = ( x ∗ h ) [ n ] = ∑ k = 0 M − 1 x [ n − k ] h [ k ] y[n] = (x * h)[n] = \sum_{k=0}^{M-1} x[n-k] h[k] y[n]=(x∗h)[n]=k=0∑M−1x[n−k]h[k]
矩阵向量乘积到频域乘积
③→②[循环矩阵和BCCB矩阵的对角化,即特征值分解,特征值是傅里叶系数,特征向量是傅里叶变换基。](https://blog.csdn.net/u013600306/article/details/143728757?spm=1001.2014.3001.5501)
总结
- 时域卷积 和 频域乘积 通过傅里叶变换和逆傅里叶变换相互转换。
- 时域卷积 和 矩阵向量乘积 通过构建卷积矩阵实现相互转换。
- 矩阵向量乘积 到 时域卷积 通过提取卷积矩阵中的冲激响应实现。
相关文章:

卷积、频域乘积和矩阵向量乘积三种形式之间的等价关系与转换
线性移不变系统 线性移不变系统(Linear Time-Invariant System, LTI系统)同时满足线性和时不变性两个条件。 线性:如果输入信号的加权和通过系统后,输出是这些输入信号单独通过系统后的输出的相同加权和,那么该系统就…...
 v-model 在原始Dom元素、自定义输入组件中双向绑定的底层实现原理详解)
【Vue】Vue3.0(二十二) v-model 在原始Dom元素、自定义输入组件中双向绑定的底层实现原理详解
上篇文章 【Vue】Vue3.0(二十一)Vue 3.0中 的$event使用示例 🏡作者主页:点击! 🤖Vue专栏:点击! ⏰️创作时间:2024年11月11日17点30分 文章目录 1. v-model 用于 HTML 标…...
史上最强大的 S3 API?介绍 Prompt API。
迄今为止,对象存储世界已由 PUT 和 GET 的 S3 API 概念定义。然而,我们现在生活的世界需要更多。鉴于 MinIO 的 S3 部署甚至比 Amazon 还多,因此我们不得不提出下一个出色的 S3 API。 这个新 API 就是 Prompt API,它很可能成为有…...

单片机设计智能翻译手势识别系统
目录 前言 一、本设计主要实现哪些很“开门”功能? 二、电路设计原理图 电路图采用Altium Designer进行设计: 三、实物设计图 四、程序源代码设计 五、获取资料内容 前言 在全球化的浪潮下,语言的多样性也为人们的交流带来了不小的挑战…...

「Mac玩转仓颉内测版12」PTA刷题篇3 - L1-003 个位数统计
本篇将继续讲解PTA平台上的题目 L1-003 个位数统计,通过对数字的处理与统计,掌握基础的字符串操作与数组计数功能,进一步提升Cangjie编程语言的实际应用能力。 关键词 PTA刷题数字统计数组操作字符串处理编程技巧 一、L1-003 个位数统计 题…...

飞书文档只读限制复制
飞书文档只读限制复制 场景描述解决方式插件安装测试 场景描述 当使用飞书时,可能会存在无对方文档编辑/管理权限,对方只给自己开放只读权限的时候,此时如果文档较重要,需要本地保存一份,但是又无法复制文档或直接屏蔽…...

【WPF】Prism学习(二)
Prism Commands 1.命令(Commanding) 1.1. ViewModel的作用: ViewModel不仅提供在视图中显示或编辑的数据,还可能定义一个或多个用户可以执行的动作或操作。这些用户可以通过用户界面(UI)执行的动作或操作…...

【鸿蒙开发】第二十一章 Location位置服务
目录 1 简介 1.1 Location Kit简介 1.2 运作机制 1.3 约束与限制 2 位置服务开发 2.1 申请位置权限开发指导 2.1.1 场景概述 2.2 获取设备的位置信息开发指导 2.2.1 场景概述 2.2.2 接口说明 2.2.3 开发步骤 2.3(逆)地理编码转化开发指导 2.…...

《目标检测》R-CNN网络基础(RCNN,Fast-RCNN)
文章目录 1.Overfeat模型2.RCNN网络2.1 算法流程2.1.1 候选区域的生成(了解,已经不再使用了)2.1.2 CNN网络提取特征2.1.3 目标分类(SVM)2.1.4 目标回归(线性回归修正坐标)2.1.5 预测过程 2.2 算…...

iOS中的定位实现(逆地理编码)及Info.plist位置权限详解
引言 在现代移动应用开发中,位置服务已经成为不可或缺的一部分。无论是地图导航、社交分享,还是基于位置的个性化推荐,位置数据都为用户提供了更加丰富和智能的体验。然而,随着用户隐私保护的不断加强,iOS对位置权限的…...

【从零开始的LeetCode-算法】3270. 求出数字答案
给你三个 正 整数 num1 ,num2 和 num3 。 数字 num1 ,num2 和 num3 的数字答案 key 是一个四位数,定义如下: 一开始,如果有数字 少于 四位数,给它补 前导 0 。答案 key 的第 i 个数位(1 < …...

Web认证机制 Cookie、Token、Session、JWT、OAuth2 解析
标题 一、Cookie二、Session三、Token四、JWTSSO(单点登录) 五、OAuth2如何设计权限系统区别总结 Cookie、Token、Session 和 JWT 都是在 Web 开发中常用的身份验证和授权技术,它们各有优缺点,适用于不同的场景。 Cookie 简单易用…...

Docker 基础命令介绍和常见报错解决
介绍一些 docker 可能用到的基础命令,并解决三个常见报错: 权限被拒绝(Permission Denied)无法连接到 Docker 仓库(Timeout Exceeded)磁盘空间不足(No Space Left on Device) 命令以…...
如何轻松导出所有 WordPress URL 为纯文本格式
作为一名多年的 WordPress 使用者,我深知管理一个网站的复杂性。从迁移网站、设置重定向到整理内容结构,每一步都需要精细处理。而拥有所有 URL 的清单,不仅能让这些工作变得更加简单,还能为后续的管理提供极大的便利。其实&#…...
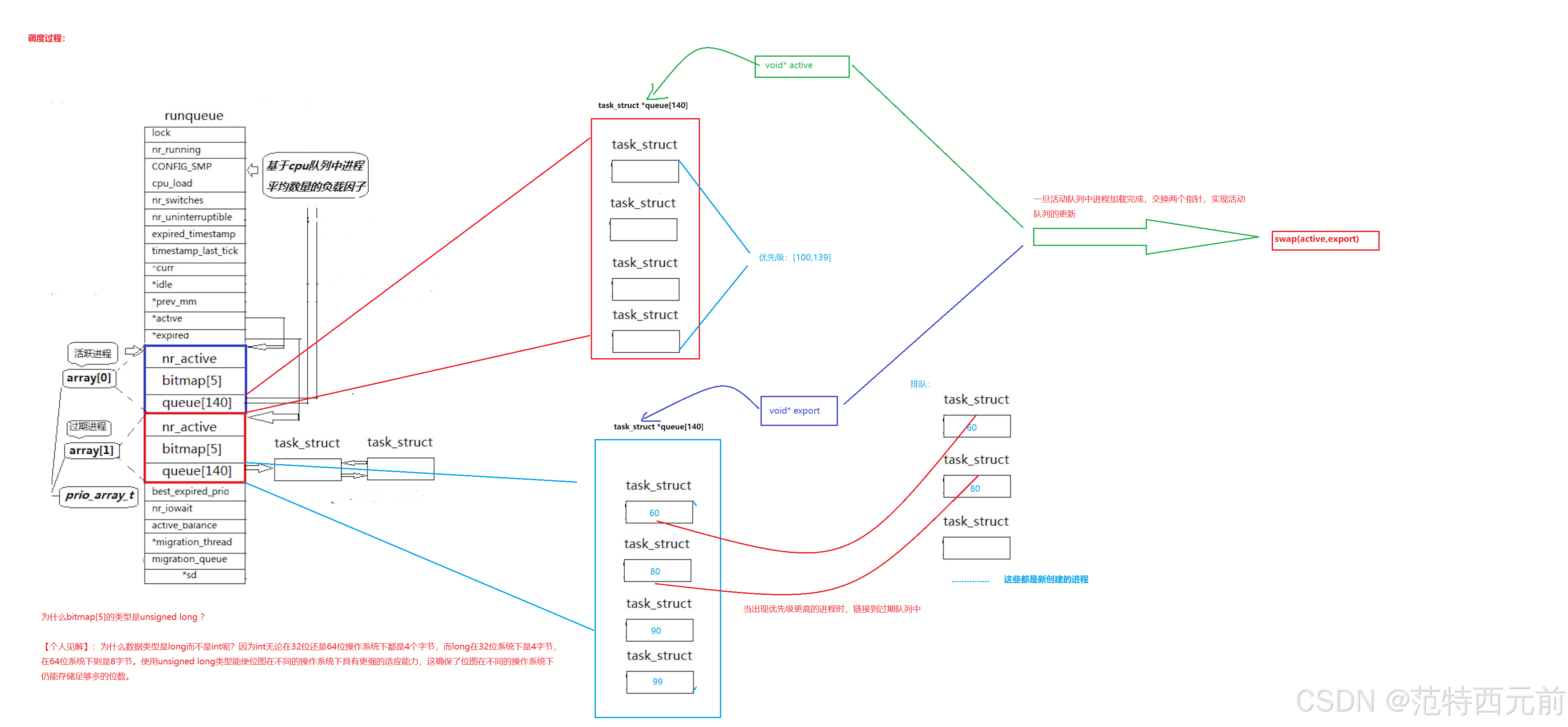
【进程概念精讲】
Susan,在那命运月台前面,再上车,春天开始落叶.................................................................. 文章目录 前言 一、【认识进程】 1、【进程基本概念引入】 2、【进程的描述与组织——进程控制块(PCB)与进程…...

帽子矩阵--记录
帽子矩阵 H是一个重要的统计工具,用于评估数据点对模型拟合结果的影响。通过计算帽子矩阵的对角线元素(杠杆值),我们可以识别出高杠杆点,这些点对模型的影响较大,可能需要特别关注。...
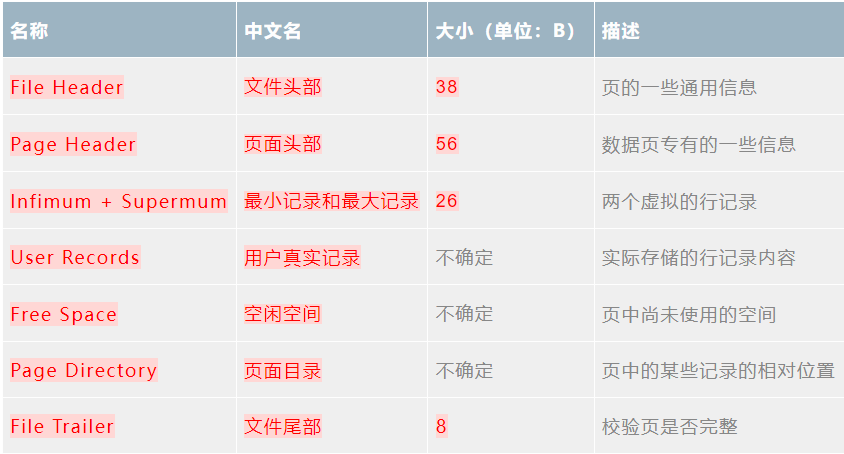
MySQL深入:B+树的演化、索引和索引结构
提示:内容是读《MySQL技术内幕:InnoDB存储引擎》,笔记摘要 文章目录 二叉查找树平衡二叉树(AVL) B树(BTree)B树(BTree)InnoDB B树索引索引结构(InnoDB B树)B树存放的数据量 二叉查找树 在二叉查找树中,左子…...

axios 实现 无感刷新方案
实现思路 首次登录前端通过接口获取到两个 token;分别是 accessToken、refreshToken; accessToken:正常请求需要传递的 token ;refreshToken:当某个请求 401 ,就可以通过 refreshToken 获取到新的 accessToken 特殊场…...

Python 三种方式实现自动化任务
在这篇文章中,我们将介绍一些用Python实现机器人过程自动化的包。机器人流程自动化(Robotic process automation,简称RPA)是指将鼠标点击和键盘按压自动化的过程,即模拟人类用户的操作。RPA用于各种应用程序࿰…...

新型创业模式:退休创业。没有工资,不用投资,有时间就干,不强制做,赚钱按贡献分。
这种“退休创业”的创业模式具有独特的吸引力和灵活性,适合那些已退休但希望继续贡献社会价值、赚取额外收入且无需承担太多责任的群体。以下是一个详细的设计思路: 模式概述 目标人群:退休人员,具有一定技能或经验,但…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...
