c++实现中缀表达式 转换为后缀表达式
使用栈来计算后缀表达式的值:
9+(3 - 1)*3+10/2;
后缀表达式:所有的符号都是在运算数字的后面出现: 9 3 1 – 3 * + 10 2 / +
规则:
中缀表达式转后缀表达式:
1.从左到右遍历中缀表达式的每个数字和符号,若是数字就打印同时入栈数字栈snum;
2.若是左括号,则将其压入运算符栈sope中;
3.若是右括号,则将sope栈顶的运算符弹出并打印,直到遇到左括号(左括号也出栈,但不输出打印);
4.若是运算符,若该运算符的优先级大于栈顶运算符的优先级时,则把它压栈;若小于或等于栈顶运算符优先级时,则将栈顶运算符弹出并打印, 同时出栈snum数字按照此运算符运算后结果入栈,再比较新的栈顶运算符,按同样方法处理,直到该运算符大于栈顶运算符优先级为止,然后将该运算符压栈;
5.若中缀表达式中的各对象处理完毕,则把sope栈中存留的运算符依次弹栈输出打印, 同时取snum中的值按照此运算符运算后的结果入栈,直至sope栈空 。snum栈底元素出栈即为计算结果。
计算规则:
- 创建一个双精度数字栈
snum来存储操作数。Copy- 使用
stringstream将输入字符串postfix便于逐个提取 token。- 使用
while (ss >> token)循环来逐个读取 token,直到字符串流结束。每次读取都会跳过空格。- 如果 token 的第一个字符是数字(使用
isdigit函数判断),则将这个 token 转换为double类型并推入栈中。- 如果 token 不是数字,说明它是一个操作符。
- 从栈中弹出两个元素(x 和 y),注意:弹出顺序是后进先出(LIFO),所以首先弹出的将是最近进入栈的数字
- 根据操作符执行相应的数学运算,并将计算结果压入栈中。
- 针对除法,还需检查除数
y是否为零,如果是,则抛出异常以避免除以零错误。- 最后,函数返回栈顶元素,这个值是后缀表达式的计算结果.
完整代码:
#include <iostream>
#include <string>
#include <exception>
#include <sstream>
#include <cstdio>
#include <cstring>
#include <stack>
using namespace std;
bool isvalidexpression(const string & expression)
{
for (char ch : expression)
{
if (!isdigit(ch) && ch != '+' && ch != '-' && ch != '*' && ch != '/' && ch != ' ')
{
return false;
}
}
return true;
}int precedence(char ch)
{
switch (ch)
{
case '+':
case'-':
return 1;
case '*':
case '/':
return 2;
default:
return 0;}
}string infixtopostfix(const string& expression)
{
stack<char> sope;//字符栈
string postfix = "";//后缀表达式
string numbuff = "";
for (size_t i = 0; i < expression.length(); i++)
{
char ch = expression[i];
if (isdigit(ch))
{
numbuff += ch;
}
else
{
if (!numbuff.empty())
{
postfix += numbuff;
postfix += ' ';
numbuff.clear();
}
if (ch == '(')
{
sope.push(ch);
}
else if (ch == ')')
{
while (!sope.empty() && sope.top() != '(')
{
postfix += sope.top();
postfix += ' ';
sope.pop();
}
sope.pop();//出栈'('
}
else
{
while (!sope.empty() && precedence(sope.top()) >= precedence(ch))
{
postfix += sope.top();
postfix += ' ';
sope.pop();
}
sope.push(ch);
}
}
}
if (!numbuff.empty())
{
postfix += numbuff;
postfix += ' ';
}
while (!sope.empty())
{
postfix += sope.top();
postfix += ' ';
sope.pop();
}if (!postfix.empty() && postfix.back() == ' ')
{
postfix.pop_back();
}
return postfix;}
double evaluatepostfix(const string& postfix)
{
stack<double>snum;//数字栈
stringstream ss(postfix);
string token;
while (ss >> token)
{
if (isdigit(token[0]))
{
snum.push(stod(token));//stod是一个函数,用于将字符串转换为double类型的浮点数。
}
else
{
double x = snum.top(); snum.pop();
double y = snum.top(); snum.pop();
switch (token[0])
{
case '+':snum.push(x + y); break;
case'-':snum.push(x - y); break;
case '*':snum.push(x * y); break;
case '/':if (y != 0)
{
snum.push(x / y);
}
else
{
throw runtime_error("Error:Division By Zero");
}
break;
}
}
}return snum.top();
}int main()
{
//输入一个表达式
string expression;
cout << "请输入一个算数表达式:(例如2*3*(4+5))" << endl;
getline(cin , expression);//检测有效性
if (!isvalidexpression(expression))
{
cout << "表达式不合法" << endl;
}
//将中缀表达式转换为后缀表达式
string postfix = infixtopostfix(expression);
cout << "后缀表达式是:"<<postfix << endl;//计算后缀表达式的值
try
{
double result = evaluatepostfix(postfix);
cout << "后缀表达式的结果为:" << result << endl;
}
catch (runtime_error& e)
{
cout << e.what() << endl;
}system("pause");
return 0;
}
相关文章:

c++实现中缀表达式 转换为后缀表达式
使用栈来计算后缀表达式的值: 9(3 - 1)*310/2; 后缀表达式:所有的符号都是在运算数字的后面出现: 9 3 1 – 3 * 10 2 / 规则: 中缀表达式转后缀表达式: 1.从左到右遍历中缀表达式的每个数字和符号,若是数字就打印同时入栈数…...

Cisco FMC重置SmartLicense到Evaluatin mode步骤
1 科普: what is FMC full name is Firepower Management Center, 是思科FirePower防火墙的统一管理平台. 能管理ASA不? no,只能管理FTD模式的墙。这里的FTD包括物理机firepower系列运行的FTD,以及FTDv(虚拟化版本&a…...

多表查询综合归纳
目录 1. 多表关系 1.1 一对多(多对一) 1.2 多对多 1.3 一对一 2. 多表查询概述 2.1 熟悉表 2.2 笛卡尔积 2.3 消除笛卡尔积 2.4 多表查询分类 3. 内连接 3.1 隐式内连接 3.2 显式内连接 4. 外连接 4.1 左外连接 4.2 右外连接 5. 自连接 …...

【5.线性表-链式表示-王道课后算法题】
王道数据结构-第二章-链式表示算法题 1.在带头结点的单链表L中,删除所有值为x的结点,并释放其空间,假设值为x的结点不唯一,试编写算法以实现上述操作。2. 试编写在带头结点的单链表L中删除一个最小值结点的高效算法(假设该结点唯一…...

存储过程及练习
1.存储过程 📖什么是存储过程? 存储过程和函数是事先经过编译并存储在数据库中的一段sql语句集合,调用存储过程函数可以简 化应用开发人员的很多工作,减少数据在数据库和应用服务器之间的传输,对于提高数据处理的 效率…...

【在Linux世界中追寻伟大的One Piece】多路转接epoll
目录 1 -> I/O多路转接之poll 1.1 -> poll函数接口 1.2 -> poll的优点 1.3 -> poll的缺点 1.4 -> poll示例 1.4.1 -> 使用poll监控标准输入 2 -> I/O多路转接之epoll 2.1 -> 初识epoll 2.2 -> epoll的相关系统调用 2.2.1 -> epoll_cre…...

设计模式-参考的雷丰阳老师直播课
一般开发中使用的模式为模版模式策略模式组合,模版用来定义骨架,策略用来实现细节。 模版模式 策略模式 与模版模式特别像,模版模式会定义好步骤定义好框架,策略模式定义小细节 入口类 使用模版模式策略模式开发支付 以上使用…...

Python +Pyqt5 简单视频爬取学习(一)
文章目录 前言 一、演示 二、查找网页视频流的索引文件 三、分析视频流的url和视频流索引文件的差异性 四、判断视频数据是否需要转化为ts 五、判断视频是否被加密,如若被加密,需要先解密 六、合并所有的ts视频,以MP4模式输出完整视频 总结 前…...

Python Requests模块全面教程
Python Requests模块全面教程 在现代软件开发中,网络请求是一个不可或缺的部分。无论是获取网页数据、调用API接口,还是进行数据交互,都会涉及到HTTP请求。Python的Requests模块是一个非常强大的库,能够让我们轻松地发送HTTP请求…...

PyQt入门指南六十 与Python其他库的集成方法
PyQt是一个强大的GUI库,它可以与Python的其他库无缝集成,以实现更复杂的功能。以下是一些常见的集成方法和示例: 1. NumPy NumPy是Python中用于科学计算的基础库。您可以在PyQt应用程序中使用NumPy来处理数据和进行数值计算。 import sys …...

Android15之解决:Dex checksum does not match for dex:framework.jar问题(二百三十九)
简介: CSDN博客专家、《Android系统多媒体进阶实战》一书作者 新书发布:《Android系统多媒体进阶实战》🚀 优质专栏: Audio工程师进阶系列【原创干货持续更新中……】🚀 优质专栏: 多媒体系统工程师系列【…...
)
车企自动驾驶功能策略 --- 硬件预埋(卷传感器配置)
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 屏蔽力是信息过载时代一个人的特殊竞争力,任何消耗你的人和事,多看一眼都是你的不对。非必要不费力证明自己,无利益不试图说服别人,是精神上的节…...

【已为网站上传证书,却显示不安全】
已为网站上传证书,却显示不安全 错误显示解决办法分析原因 错误显示 此站点有一个由受信任的颁发机构颁发的有效证书但是网站的某些部分不安全 解决办法 删除浏览器所有历史记录, 如果是Edge浏览器显示不安全,那就删除Edge浏览器的所有历史记录; 如果是Google Chrome浏览器显…...

docker busybox作为initContainers
一、上传到私有仓储 docker pull busybox:1.33.1 docker tag busybox:1.33.1 192.168.31.185/public/busybox:1.33.1 docker push 192.168.31.185/public/busybox:1.33.1 --- apiVersion: apps/v1 kind: Deployment metadata:annotations: {}labels: {}name: saas-ali-apiname…...
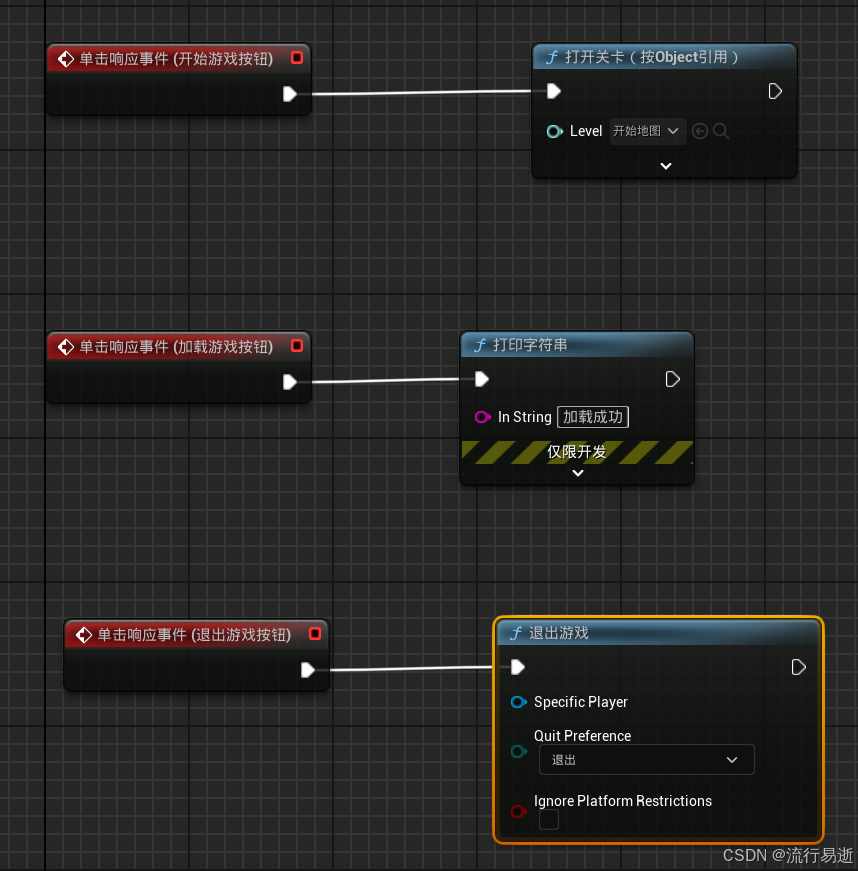
20.UE5UI预构造,开始菜单
2-22 开始菜单、事件分发器、UI预构造_哔哩哔哩_bilibili 目录 1.UI预构造 2.开始菜单和开始关卡 2.1开始菜单 2.2开始关卡 2.3将开始菜单展示到开始关卡 3.事件分发器 1.UI预构造 如果我们直接再画布上设计我们的按钮,我们需要为每一个按钮进行编辑&#x…...

Electron教程1-初学入门
玩转Electron Electron 是什么注意事项环境安装安装 vscode安装 git 第一个实例第二个实例第二个实例解读 总结问题解答 Electron 是什么 Electron是一个使用 JavaScript、HTML 和 CSS 构建桌面应用程序的框架。 嵌入 Chromium 和 Node.js 到 二进制的 Electron 允许您保持一个…...

从北美火到中国,大数据洞察品牌“STANLEY”的突围之路
保守直筒大头的“硬汉”外形,以百变颜色踩中时尚命脉,与各路大牌“梦幻联动”,不少时尚弄潮儿没能逃过其“真香”诱惑。 这就是今年以来从北美火到中国的STANLEY,在“巨无霸”水杯中突围出属于自己的一条路。 最近STANLEY又整活…...

深度学习之GAN应用
1 GAN的应用(文本生成) 1.1 GAN为什么不适合文本任务? GAN在2014年被提出之后,在图像生成领域取得了广泛的研究应用。然后在文本领域却一直没有很惊艳的效果。主要在于文本数据是离散数据,而GAN在应用于离散数据时…...

鸿蒙生态下的安全隐私保护:打造用户信任的应用体验
鸿蒙生态下的安全隐私保护:打造用户信任的应用体验 随着华为鸿蒙系统的快速发展,越来越多的设备开始支持这一操作系统,不仅限于智能手机,还包括智能穿戴设备、智能家居产品等。作为开发者,在享受鸿蒙生态系统带来的广…...

用pandoc工具实现ipynb,md,word,pdf之间的转化
Pandoc 是一个强大的工具,可以实现多种文件格式之间的转换,包括 Jupyter Notebook (.ipynb)、Markdown (.md)、Word (.docx)、PDF 等格式。以下是具体的实现方法: 1. 安装 Pandoc 确保已安装 Pandoc: Linux: sudo apt install p…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...
