LabVIEW中坐标排序与旋转 参见附件snippet程序
LabVIEW中坐标排序与旋转 参见附件snippet程序LabVIEW中坐标排序与旋转 参见附件snippet程序 - 北京瀚文网星科技有限公司
在LabVIEW中处理坐标排序的过程,尤其是按顺时针或逆时针排列坐标点,常见的应用包括处理几何形状、路径规划等任务。下面我将为您提供一个参考例子,展示如何实现按顺时针排列四个坐标点。您可以根据这个例子来理解该方法,并应用于自己的项目中。
参考例子:按顺时针排列四个坐标点
假设我们有四个坐标点,分别为 (X1, Y1), (X2, Y2), (X3, Y3), (X4, Y4),需要将它们按顺时针方向排列。
1. 输入数据
我们使用四个坐标作为输入:
-
坐标1:
(X1, Y1) = (1, 3) -
坐标2:
(X2, Y2) = (4, 4) -
坐标3:
(X3, Y3) = (3, 1) -
坐标4:
(X4, Y4) = (2, 2)
2. 计算质心
质心是四个点的 X 和 Y 坐标的平均值。计算方式如下:
CentroidX=X1+X2+X3+X44CentroidX=4X1+X2+X3+X4CentroidY=Y1+Y2+Y3+Y44CentroidY=4Y1+Y2+Y3+Y4
在这个例子中:
CentroidX=1+4+3+24=2.5CentroidX=41+4+3+2=2.5CentroidY=3+4+1+24=2.5CentroidY=43+4+1+2=2.5
所以,质心的坐标是 (2.5, 2.5)。
3. 计算每个坐标的角度
对于每个坐标点,我们计算其相对于质心的角度,使用 atan2 函数(LabVIEW内建的极坐标转换函数)来计算坐标相对于质心的角度:
θi=atan2(Yi−CentroidY,Xi−CentroidX)θi=atan2(Yi−CentroidY,Xi−CentroidX)
-
对于点
θ1=atan2(3−2.5,1−2.5)=atan2(0.5,−1.5)≈2.8198radiansθ1=atan2(3−2.5,1−2.5)=atan2(0.5,−1.5)≈2.8198 radians(X1, Y1) = (1, 3),角度计算为: -
对于点
θ2=atan2(4−2.5,4−2.5)=atan2(1.5,1.5)≈0.7854radiansθ2=atan2(4−2.5,4−2.5)=atan2(1.5,1.5)≈0.7854 radians(X2, Y2) = (4, 4),角度计算为: -
对于点
θ3=atan2(1−2.5,3−2.5)=atan2(−1.5,0.5)≈−1.2490radiansθ3=atan2(1−2.5,3−2.5)=atan2(−1.5,0.5)≈−1.2490 radians(X3, Y3) = (3, 1),角度计算为: -
对于点
θ4=atan2(2−2.5,2−2.5)=atan2(−0.5,−0.5)≈−2.3562radiansθ4=atan2(2−2.5,2−2.5)=atan2(−0.5,−0.5)≈−2.3562 radians(X4, Y4) = (2, 2),角度计算为:
4. 排序坐标
将角度和坐标打包成簇,并按照角度排序。排序后的角度将对应于顺时针排列的坐标顺序。
排序后得到角度和坐标如下:
-
(X2, Y2) = (4, 4),角度为0.7854 -
(X1, Y1) = (1, 3),角度为2.8198 -
(X3, Y3) = (3, 1),角度为-1.2490 -
(X4, Y4) = (2, 2),角度为-2.3562
5. LabVIEW实现
a. 数据结构
首先,创建一个包含四个坐标点的数组(XY 数据)。然后将每个坐标与其角度打包成一个簇。
b. 计算质心
使用公式计算质心的 X 和 Y 坐标。
c. 计算角度
利用 atan2 函数,计算每个坐标点的角度。
d. 排序
创建一个数组,包含每个坐标和其对应的角度。然后使用LabVIEW的 Sort 1D Array 函数对角度进行排序,得到顺时针顺序的坐标。
e. 输出结果
输出排序后的坐标数组,即按顺时针顺序排列的坐标点。
6. 代码实现简要示例
-
输入四个坐标点:创建四个
XY数据。 -
计算质心:分别计算
X和Y的平均值。 -
计算每个点的角度:使用
atan2函数计算角度。 -
创建包含坐标和角度的簇:将坐标与对应的角度打包。
-
排序:使用
Sort 1D Array对角度进行排序。 -
提取排序后的坐标:输出按顺时针排列的坐标。
七、总结
这个例子演示了如何在LabVIEW中根据坐标的角度将四个点按顺时针排列。通过计算质心、角度,并使用排序函数,我们能够轻松地处理坐标排序问题。该方法不仅适用于四个点的情况,也可以扩展到更多坐标点的顺时针排序问题。

如果给定了一个“中线点”作为参考点,并且要求按顺时针方向排序其余三个点的坐标,可以按照以下步骤进行操作。
步骤一:确定中线点的位置
假设你提到的“中线点”是四个点的几何中心。几何中心(质心)是四个点坐标的平均值,表示四个点的“中心点”。根据给定的四个点:
(244,488),(439,498),(259,704),(453,713)(244,488),(439,498),(259,704),(453,713)
几何中心的坐标计算方法是:
centroidx=x1+x2+x3+x44centroidx=4x1+x2+x3+x4centroidy=y1+y2+y3+y44centroidy=4y1+y2+y3+y4
代入给定坐标:
centroidx=244+439+259+4534=13954=348.75centroidx=4244+439+259+453=41395=348.75centroidy=488+498+704+7134=24034=600.75centroidy=4488+498+704+713=42403=600.75
所以,中线点(几何中心)是 (348.75, 600.75)。
步骤二:计算其他点与中线点的相对角度
接下来,我们需要根据几何中心 (348.75, 600.75) 计算每个点的极角,来确定它们相对于中线点的位置。使用相同的极角公式:
θ=atan2(y−y0,x−x0)θ=atan2(y−y0,x−x0)
其中 (x0,y0)(x0,y0) 是中线点 (348.75,600.75)(348.75,600.75),(x,y)(x,y) 是其他三个点的坐标,atan2atan2 是计算极角的反正切函数。
我们依次计算每个点的角度。
-
点 (244, 488):
θ1=atan2(488−600.75,244−348.75)=atan2(−112.75,−104.75)≈−2.288radiansθ1=atan2(488−600.75,244−348.75)=atan2(−112.75,−104.75)≈−2.288 radians -
点 (439, 498):
θ2=atan2(498−600.75,439−348.75)=atan2(−102.75,90.25)≈−0.878radiansθ2=atan2(498−600.75,439−348.75)=atan2(−102.75,90.25)≈−0.878 radians -
点 (259, 704):
θ3=atan2(704−600.75,259−348.75)=atan2(103.25,−89.75)≈2.349radiansθ3=atan2(704−600.75,259−348.75)=atan2(103.25,−89.75)≈2.349 radians -
点 (453, 713):
θ4=atan2(713−600.75,453−348.75)=atan2(112.25,104.25)≈0.756radiansθ4=atan2(713−600.75,453−348.75)=atan2(112.25,104.25)≈0.756 radians
步骤三:按顺时针顺序排序
根据角度值,进行排序:
-
θ1≈−2.288θ1≈−2.288(点 (244, 488))
-
θ2≈−0.878θ2≈−0.878(点 (439, 498))
-
θ4≈0.756θ4≈0.756(点 (453, 713))
-
θ3≈2.349θ3≈2.349(点 (259, 704))
顺时针排序的结果为:
(244,488)→(439,498)→(453,713)→(259,704)(244,488)→(439,498)→(453,713)→(259,704)
结果
按顺时针方向排序后的四个点的顺序是:
(244,488),(439,498),(453,713),(259,704)(244,488),(439,498),(453,713),(259,704)
计算过程总结:
-
计算几何中心(中线点),即四个点的平均坐标。
-
计算每个点与几何中心的相对角度(极角)。
-
按照极角进行排序,得到顺时针方向的顺序。
所用functon解释说明:
Inverse Tangent (2 Input) Function
所属面板:三角函数(Trigonometric Functions)
要求:基本开发系统(Base Development System)
功能:计算 yxxy 的反正切(arctangent)。
该函数能够计算在 x-y 平面 中四个象限的反正切值,而普通的反正切(Inverse Tangent)函数只能计算两个象限的反正切值。此函数提供了更广泛的应用,因为它能够确定角度的正确象限。
连接器面板(Connector Pane):显示该多态函数的默认数据类型。
翻译与解释
-
Inverse Tangent (2 Input) Function:该函数是计算反正切的函数,接收两个输入参数:yy 和 xx,并返回 θ=atan2(y,x)θ=atan2(y,x),其中 θθ 是从 xx-轴到点 (x,y)(x,y) 的角度。
-
四个象限的反正切:该函数能够正确处理四个象限的情况(即负值和正值的组合),这是普通的反正切函数无法做到的。普通的反正切函数(atan)只能处理从 −π2−2π 到 π22π 的角度,无法区分哪些角度在第二或第三象限。因此,atan2 函数是更为通用和准确的选择,尤其是当你需要处理带符号的坐标时。
-
示例:给定 y=−112.75y=−112.75 和 x=−104.75x=−104.75,使用 atan2 函数计算时,它会返回一个负值的角度,指示该点位于第三象限。而普通的 atan 函数则无法直接处理这一点,因为它只会返回一个在 -90° 到 +90° 范围内的角度,无法区分象限。
小结:
LabVIEW 中的 Inverse Tangent (2 Input) 函数(即 atan2)是一个更灵活的反正切函数,可以处理四个象限中的任何情况,并返回正确的角度(弧度值)。
相关文章:

LabVIEW中坐标排序与旋转 参见附件snippet程序
LabVIEW中坐标排序与旋转 参见附件snippet程序LabVIEW中坐标排序与旋转 参见附件snippet程序 - 北京瀚文网星科技有限公司 在LabVIEW中处理坐标排序的过程,尤其是按顺时针或逆时针排列坐标点,常见的应用包括处理几何形状、路径规划等任务。下面我将为您…...
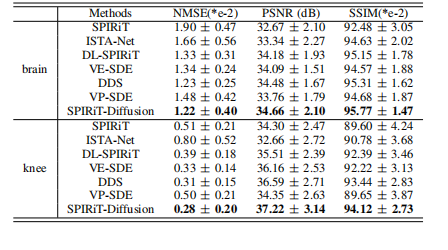
SPIRiT-Diffusion:基于自一致性驱动的加速MRI扩散模型|文献速递-基于深度学习的病灶分割与数据超分辨率
Title 题目 SPIRiT-Diffusion: Self-Consistency Driven Diffusion Model for Accelerated MRI SPIRiT-Diffusion:基于自一致性驱动的加速MRI扩散模型 01 文献速递介绍 磁共振成像(MRI) 在临床和研究领域被广泛应用。然而,其…...

jwt封装教程
使用步骤: 1.导入jwt相关依赖 2.创建jwt工具类方便使用 3.通过工具类提供的方法进行生成jwt 4.通过工具类解析jwt令牌获取封装的数据 5.设定拦截器,每次执行请求的时候都需要验证token 6.注册拦截器 1.jwt依赖 <dependency><groupId>io.json…...

postman变量和脚本功能介绍
1、基本概念——global、collection、environment 在postman中,为了更好的管理各类变量、测试环境以及脚本等,创建了一些概念,包括:globals、collection、environment。其实在postman中,最上层还有一个Workspaces的概…...

【AI新领域应用】AlphaFold 2,原子级别精度的蛋白质3D结构预测,李沐论文精读(2021Nature封面,2024诺贝尔奖)
文章目录 AlphaFold 2 —— 原子级别精度的蛋白质3D结构预测背景(2024诺奖与AI学习资料)1、摘要、导论、写作技巧2、方案:模型,编码器,解码器3、实验:数据集,训练,结果 AlphaFold 2 …...

Figma汉化:提升设计效率,降低沟通成本
在UI设计领域,Figma因其强大的功能而广受欢迎,但全英文界面对于国内设计师来说是一个不小的挑战。幸运的是,通过Figma汉化插件,我们可以克服语言障碍。以下是两种获取和安装Figma汉化插件的方法,旨在帮助国内的UI设计师…...

前端知识点---this的用法 , this动态绑定(Javascript)
文章目录 this动态绑定 , this的用法01. 全局作用域下的 this02. 函数中的 this2.1 普通函数调用2.2 构造函数调用2.3 箭头函数中的 this 03对象方法调用04. 事件处理中的 this05. 动态绑定的方式5.1 call 方法5.2 apply 方法5.3 bind 方法 06类中的 this07. 总结 this动态绑定…...

web——upload-labs——第五关——大小写绕过绕过
先上传一个 先尝试直接上传一个普通的一句话木马 不行 可以看到,.htaccess文件也被过滤了,我们来查看一下源码 第五关的源码没有把字符强制转换为小写的语句: $file_ext strtolower($file_ext); //转换为小写 直接通过Burpsuite抓包修改文…...

String类型
String类 在Java中,String 类是一个非常核心且常用的类,它用于表示文本值,即字符序列或者说字符串。 1.1 类的声明 public final class Stringimplements java.io.Serializable, Comparable<String>, CharSequence 解释:…...

Ubuntu24.04安装和配置Redis7.4
Ubuntu24.04安装和配置Redis7.4 #切换到root用户 sudo su -#更新源 apt update apt upgrade#安装 lsb-release、curl 和 gpg ,以便能够添加 Redis 仓库 apt install lsb-release curl gpg#导入 Redis 的 GPG 密钥 curl -fsSL https://packages.redis.io/gpg | gpg …...

权限相关知识
1.Linux权限的概念 在说Linux权限的概念之前我来问大家一个问题,你们觉得什么是权限? 权限平时的体现呢,就比如不是校长的亲戚就不能逛办公室,没充会员的爱奇艺看不了VIP影视剧,没成会员的的蛋糕店拿不到会员价等等等…...

【时间之外】IT人求职和创业应知【37】-AIGC私有化
目录 新闻一:2024智媒体50人成都会议暨每经20周年财经媒体峰会召开 新闻二:全球机器学习技术大会在北京召开 新闻三:区块链技术在金融领域的应用取得新突破 不知不觉的坚持了1个月,按照心理学概念,还要坚持2个月&am…...
深入理解 source 和 sh、bash 的区别
1 引言 在日常使用 Linux 的过程中,脚本的执行是不可避免的需求之一,而 source、sh、bash 等命令则是执行脚本的常用方式。尽管这些命令都能运行脚本,但它们之间的执行方式和效果却有着显著的区别。这些区别可能会影响到脚本的环境变量、工作…...

k8clone二进制工具迁移k8s中的无状态应用
1 概述 k8clone是一个简便的Kubernetes元数据克隆工具,它可以将Kubernetes元数据(对象)保存为本地压缩包,在恢复时可将这些元数据恢复到目标集群中(已存在的资源不会被覆盖)。它不依赖远程存储,…...

VPI photonics的一些使用经验(测相位 快速搜索)持续更新
1.使用FuncSinEl模块的注意事项: 2.在VPI player(示波器)测电信号相位时候,可以使用正则表达式,快速搜索。 比如我要搜索以30开头的数据,输入: ^30 其他的正则表达式不适用,比如以…...

DBeaver 连接 OceanBase Oracle 租户
DBeaver 是一款通用的数据库工具软件,支持任何具有JDBC驱动程序的数据库。DBeaver 需要 Java 运行环境的支持。截稿时 DBeaver 24.0.0 版本默认提供的 OceanBase 驱动是连接 MySQL 的,想连接 Oracle 租户需要新建一个驱动器使用。 下载数据库驱动包 1、…...

QT_CONFIG宏使用
时常在Qt代码中看到QT_CONFIG宏,之前以为和#define、DEFINES 差不多,看了定义才发现不是那么回事,定义如下: 看注释就知道了QT_CONFIG宏,其实是:实现了一个在编译时期安全检查,检查指定的Qt特性…...

力扣(leetcode)题目总结——辅助栈篇
leetcode 经典题分类 链表数组字符串哈希表二分法双指针滑动窗口递归/回溯动态规划二叉树辅助栈 本系列专栏:点击进入 leetcode题目分类 关注走一波 前言:本系列文章初衷是为了按类别整理出力扣(leetcode)最经典题目,…...

如何处理 iOS 客户端内 Webview H5 中后台播放的音视频问题
目录 问题描述Page Visibility API 的应用什么是 Page Visibility API?使用 Page Visibility API 暂停音视频完整解决方案1. 监听媒体的播放和暂停事件2. 防止自动播放3. 结合 Intersection Observer 进行媒体控制4. 手动处理应用生命周期中的事件 问题描述 在 iOS…...

C++的一些模版
1、不限制次数的输入数据 vector<int> nums;int num;while (cin >> num) {nums.push_back(num);if (cin.get() \n) break;}2、取模模版 template<int kcz> struct ModInt { #define T (*this)int x;ModInt() : x(0) {}ModInt(int y) : x(y > 0 ? y : y…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...

k8s从入门到放弃之Pod的容器探针检测
k8s从入门到放弃之Pod的容器探针检测 在Kubernetes(简称K8s)中,容器探测是指kubelet对容器执行定期诊断的过程,以确保容器中的应用程序处于预期的状态。这些探测是保障应用健康和高可用性的重要机制。Kubernetes提供了两种种类型…...

CVE-2023-25194源码分析与漏洞复现(Kafka JNDI注入)
漏洞概述 漏洞名称:Apache Kafka Connect JNDI注入导致的远程代码执行漏洞 CVE编号:CVE-2023-25194 CVSS评分:8.8 影响版本:Apache Kafka 2.3.0 - 3.3.2 修复版本:≥ 3.4.0 漏洞类型:反序列化导致的远程代…...
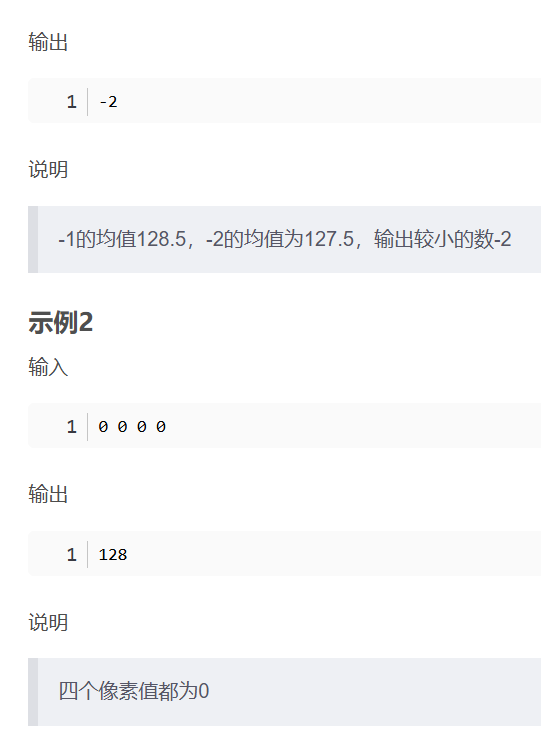
华为OD机考- 简单的自动曝光/平均像素
import java.util.Arrays; import java.util.Scanner;public class DemoTest4 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint[] arr Array…...
