二叉树Golang
二叉树
前言
- 完全二叉树
- 最底层节点按顺序从左到右排列。
- 满二叉树
- 一颗二叉树只有0度和2度的节点。
- 二叉搜索树
- 左子树上的所有节点的值均小于根节点的值。
- 右子树上的所有节点的值均大于根节点的值。
- 平衡二叉搜索树
- 左右两个子树的高度差的绝对值不超过1 。
二叉树的存储方式有链式存储和数组存储。(线索二叉树、红黑树等)
1、链表存储方式
type TreeNode struct {Val intLeft *TreeNodeRight *TreeNode
}func NewTreeNode(val int) *TreeNode {return &TreeNode{Val: val}
}
2、数组存储方式
// 完全二叉树: 1// / \// 2 3// / \ / \// 4 5 6 7// 以下为前中后序遍历,以下例子也是这个结果// 1245367 // 4251637// 4526731
左子树:2 * i + 1
右子树:2 * i + 2
(i是数组的下标),元素值为arr[ 2 * i + 1 ]或arr[ 2 * i + 2 ]
接下来将讲解二叉树的几种遍历方式,我全篇使用链式存储结构。
一、深度优先遍历
1、前序遍历
1、递归遍历
// 前序遍历:根 -> 左 -> 右
func preorderTraversal(root *TreeNode) {if root != nil {fmt.Println(root.Val) // 访问根节点preorderTraversal(root.Left) // 递归遍历左子树preorderTraversal(root.Right) // 递归遍历右子树}
}
2、迭代遍历
深度优先遍历的递归版本都是简洁易读的,相较于迭代版本,更直观。迭代版本使用到了一种数据结构栈,以下我使用的栈是自己封装的库函数,如果有感兴趣的朋友,可以看shard库介绍,写shard库主要还是由于Golang没提供更多的数据结构模版。
// 前序遍历:根 -> 左 -> 右(迭代实现)
func preorderTraversal(root *TreeNode) {if root == nil {return}// 栈存放的全是 *TreeNodes := shard.NewStackArray[*TreeNode]()s.Push(root)for s.Len() > 0 {// 栈顶弹出并删除node, _ := s.Pop()fmt.Println(node.Val)// 先压右子节点,再压左子节点,因为栈是后进先出(LIFO)if node.Right != nil {s.Push(node.Right)}if node.Left != nil {s.Push(node.Left)}}
}
2、中序遍历
1、递归遍历
// 中序遍历:左 -> 根 -> 右
func inorderTraversal(root *TreeNode) {if root != nil {inorderTraversal(root.Left) // 递归遍历左子树fmt.Println(root.Val) // 访问根节点inorderTraversal(root.Right) // 递归遍历右子树}
}
2、迭代遍历
// 中序遍历:左 -> 根 -> 右(迭代实现)
func inorderTraversal(root *TreeNode) {if root == nil {return}// 栈存放的全是 *TreeNodes := shard.NewStackArray[*TreeNode]()cur := rootfor cur != nil || !s.IsEmpty() {for cur != nil {s.Push(cur)cur = cur.Left}node, _ := s.Pop()fmt.Println(node.Val)cur = node.Right}
}
3、后序遍历
1、递归遍历
// 后序遍历:左 -> 右 -> 根
func postorderTraversal(root *TreeNode) {if root != nil {postorderTraversal(root.Left) // 递归遍历左子树postorderTraversal(root.Right) // 递归遍历右子树fmt.Println(root.Val) // 访问根节点}
}
2、迭代遍历
// 后序遍历:左 -> 右 -> 根(迭代实现)
func postorderTraversal(root *TreeNode) {if root == nil {return}// 栈存放的全是 *TreeNodes1 := shard.NewStackArray[*TreeNode]()s1.Push(root)s2 := shard.NewStackArray[*TreeNode]()for !s1.IsEmpty() {node, _ := s1.Pop()s2.Push(node)if node.Left != nil {s1.Push(node.Left)}if node.Right != nil {s1.Push(node.Right)}}for !s2.IsEmpty() {node, _ := s2.Pop()fmt.Println(node.Val)}
}
二、广度优先遍历
1、层序遍历
// 层序遍历
func postorderTraversal(root *TreeNode) {if root == nil {return}q := shard.NewQueueArray[*TreeNode]()q.Enqueue(root)for !q.IsEmpty() {node, _ := q.Dequeue()fmt.Print(node.Val, " ")if node.Left != nil {q.Enqueue(node.Left)}if node.Right != nil {q.Enqueue(node.Right)}}
}
三、shard库介绍
GitHub链接:https://github.com/xzhHas/shard
shard库获取:
go get -u github.com/xzhHas/shard@latest
关于使用Golang写一个数据结构的库,目前只支持栈、队列、堆。

相关文章:

二叉树Golang
二叉树 前言 完全二叉树 最底层节点按顺序从左到右排列。 满二叉树 一颗二叉树只有0度和2度的节点。 二叉搜索树 左子树上的所有节点的值均小于根节点的值。右子树上的所有节点的值均大于根节点的值。 平衡二叉搜索树 左右两个子树的高度差的绝对值不超过1 。 二叉树的存储…...

通过css的哪些方式可以实现隐藏页面上的元素?
1:opacity:0 通过将元素的透明度设置为o,实现隐藏效果,但是依然会占用空间并可以进行交互。 2:visibility:hidden 与透明度度为0的方案类似,会占据空间,但不可以进行交互。 3:Overflow:hi…...

微信小程序 === 使用腾讯地图选点
目录 插件介绍 接入指引 相关参数说明 插件错误处理 效果图 permission 插件的作用 添加插件 引入插件代码包 使用插件 页面 js 接口 插件介绍 腾讯位置服务地图选点插件 可以让用户快速、准确地选择并确认自己的当前位置,并将相关位置信息回传给开发者。…...
)
Redis高可用-Cluster(集群)
Redis cluster cluster 为无中心,分布式 sharding,高可用技术架构。 在哨兵 sentinel 机制中,可以解决 redis 高可用的问题,即当 master 故障后可以自动将 slave 提升为 master 从而可以保证 redis 服务的正常使用。 但是无法解…...

Spring Boot编程训练系统:数据管理与存储
摘要 随着信息技术在管理上越来越深入而广泛的应用,管理信息系统的实施在技术上已逐步成熟。本文介绍了编程训练系统的开发全过程。通过分析编程训练系统管理的不足,创建了一个计算机管理编程训练系统的方案。文章介绍了编程训练系统的系统分析部分&…...

报告解读 | 创意经济2024:如何在变革中抢占先机?
在科技飞速发展的今天,创意行业正面临前所未有的变化。《Skillshare Trendshare 2024》报告揭示了多项趋势,为创意人士提供了深刻的洞察和实用的建议。本文将为您详细解读这些趋势,助您在创意领域脱颖而出。 1. 人工智能(AI&…...

Flume1.9.0自定义Sink组件将数据发送至Mysql
需求 1、将Flume采集到的日志数据也同步保存到MySQL中一份,但是Flume目前不支持直接向MySQL中写数据,所以需要用到自定义Sink,自定义一个MysqlSink。 2、日志数据默认在Linux本地的/data/log/user.log日志文件中,使用Flume采集到…...

如何在 Ubuntu 24.04 上安装和配置 Fail2ban ?
确保你的 Ubuntu 24.04 服务器的安全是至关重要的,特别是如果它暴露在互联网上。一个常见的威胁是未经授权的访问尝试,特别是通过 SSH。Fail2ban 是一个强大的工具,可以通过自动阻止可疑活动来帮助保护您的服务器。 在本指南中,我…...

uniapp如何i18n国际化
1、正常情况下项目在代码生成的时候就已经有i18n的相关依赖,如果没有可以自行使用如下命令下载: npm install vue-i18n --save 2、创建相关文件 en文件下: zh文件下: index文件下: 3、在main.js中注册:…...

C++__day1
1、思维导图 2、如果登录失败,提示用户登录失败信息,并且提示错误几次,且重新输入;如果输入错误三次,则退出系统 #include <iostream> using namespace std;int main() {string id , pswd;string user"admi…...

Emacs进阶之插入时间信息(一百六十三)
简介: CSDN博客专家、《Android系统多媒体进阶实战》一书作者 新书发布:《Android系统多媒体进阶实战》🚀 优质专栏: Audio工程师进阶系列【原创干货持续更新中……】🚀 优质专栏: 多媒体系统工程师系列【…...

Java线程池:ThreadPoolExecutor原理解析
一、线程池的基本概念 1.1 线程池的定义 线程池是一组预先创建的线程,这些线程可以重复使用来执行多个任务,避免了频繁创建和销毁线程的开销。线程池的核心思想是通过复用一组工作线程,来处理大量的并发任务,减少系统资源消耗&a…...

二叉树、哈夫曼报文大全
1、泛型链树 #include <iostream> #include<Windows.h> #include<string> #include<stack> #include<queue> using namespace std; void menu() {cout << "**********" << endl;cout << "-1.添加" <&…...

NotePad++中安装XML Tools插件
一、概述 作为开发人员,日常开发中大部的数据是标准的json格式,但是对于一些古老的应用,例如webservice接口,由于其响应结果是xml,那么我们拿到xml格式的数据后,常常会对其进行格式化,以便阅读。…...

聊天服务器(7)数据模块
目录 Mysql数据库代码封装头文件与源文件 Mysql数据库代码封装 业务层代码不要直接写数据库,因为业务层和数据层的代码逻辑也想完全区分开。万一不想存储mysql,想存redis的话,就要改动大量业务代码。解耦合就是改起来很方便。 首先需要安装m…...

VS2022编译32位OpenCV
使用环境 Visual Studio 2022 OpenCV: 4.7.0 cmake: 3.30.2一、使用CMake工具生成vs2022的openCV工程解决方案 打开cmake,选择opencv的源代码目录,创建一个文件夹,作为VS工程文件的生成目录 点击configure构建项目,弹出构建设置…...

WP网站如何增加文章/页面的自定义模板
通过Wordpress我们后台在发布文章或者页面的时候其实可以看到有些主题 他有选择使用的页面模板,可以自定义模板,但是有些主题却没有选择主题这个功能,那这个自定义模板的功能是如何实现的呢?以下分两种情况:Page页面和…...

【Linux网络编程】简单的UDP网络程序
目录 一,socket编程的相关说明 1-1,sockaddr结构体 1-2,Socket API 二,基于Udp协议的简单通信 一,socket编程的相关说明 Socket编程是一种网络通信编程技术,它允许两个或多个程序在网络上相互通信&…...

LabVIEW中坐标排序与旋转 参见附件snippet程序
LabVIEW中坐标排序与旋转 参见附件snippet程序LabVIEW中坐标排序与旋转 参见附件snippet程序 - 北京瀚文网星科技有限公司 在LabVIEW中处理坐标排序的过程,尤其是按顺时针或逆时针排列坐标点,常见的应用包括处理几何形状、路径规划等任务。下面我将为您…...
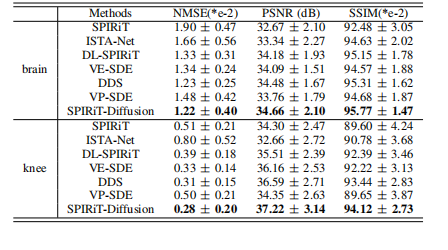
SPIRiT-Diffusion:基于自一致性驱动的加速MRI扩散模型|文献速递-基于深度学习的病灶分割与数据超分辨率
Title 题目 SPIRiT-Diffusion: Self-Consistency Driven Diffusion Model for Accelerated MRI SPIRiT-Diffusion:基于自一致性驱动的加速MRI扩散模型 01 文献速递介绍 磁共振成像(MRI) 在临床和研究领域被广泛应用。然而,其…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...
