图形几何之美系列:法向量计算之轮廓有向面积辅助法
“ 垂直于平面的直线所表示的向量为该平面的法向量,可以通过法向量识别平面正反面。法向量是轮廓或面的重要特征,求轮廓法向是一种基础的几何工具算法,在图形几何、图像处理等领域具有广泛的应用。”
-
图形几何之美系列:三维实体结构表达
-
图形几何之美系列:仿射变换矩阵
-
图形几何之美系列:仿射变换矩阵(二)
-
图形几何之美系列:仿射变换矩阵之先转后偏
-
图形几何之美系列:仿射变换矩阵之Y-Up和Z-Up
-
Unity动画:Hello World!
-
图形几何之美系列:面积计算之梯形投影求和
-
重磅发布:领略图形几何之美,向工业软件进击的小哈 #二维凸包
法向量是轮廓或面的基础几何特征,在实际工程中存在广泛的应用。在计算机视觉领域,法向量可以用于检测图像中的边缘和角点。在三维建模和渲染中,法向量可以帮助计算光线与曲面的相交,从而实现阴影效果和渲染,使图像更加真实。在立体几何中,法向量可用于求解点到平面的距离、异面直线间的距离、直线与平面所成的角、二面角的大小等问题。
1.前言
有多种方法可计算轮廓的法向量,如根据轮廓类型进行法向量的计算、轮廓有向面积辅助法、Newell向量法等。
如上文多边形轮廓面积计算中的内容所述,轮廓的法向量和面积密切相关,我们常说的法向量为单位法向量,而模长等于面积的法向量是多边形轮廓多维度的几何和物理属性,更能表达轮廓的几何特征。
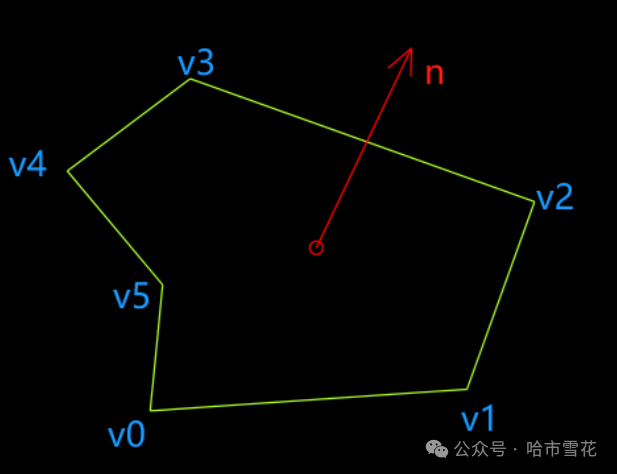
需要注意的是由于浮点数存储和运算的精度损失,可能造成求轮廓法向的精度损失,如角点由于精度损失并非精确的在一个平面上(而是在容差范围内属于一个平面)、角点距离很近导致可能进一步影响法向计算的精度等。
2.根据轮廓类型计算法向量
2.1.三角形法向量
可以通过相邻边方向叉乘得到三角形法向量,边的选择将决定得到的法向量是正向还是反向,当我们选择边与其后续邻接边进行叉乘时,得到的就是三角形正向的法向量。
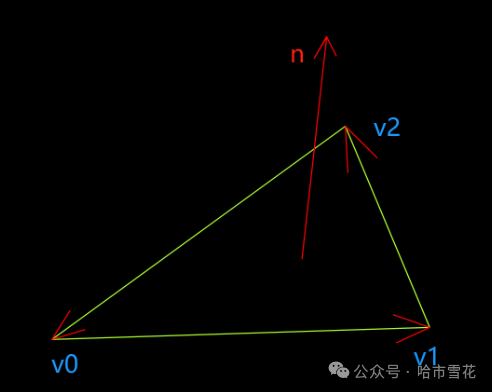
2.2.凸多边形法向量
三角形是凸多边形的类型之一,凸多边形的法向量计算同样可以用选择边与其后续邻接边进行叉乘得到。
需要注意的是由于浮点型存储和计算精度损失等原因,凸多边形上的点可能存在略微偏离所在平面,这时候参与运算的边如果恰好有非常短的边时,由其构造的相量与所在平面夹角将不为0,甚至偏离较大,这将导致求得的法向量存在较大的误差。
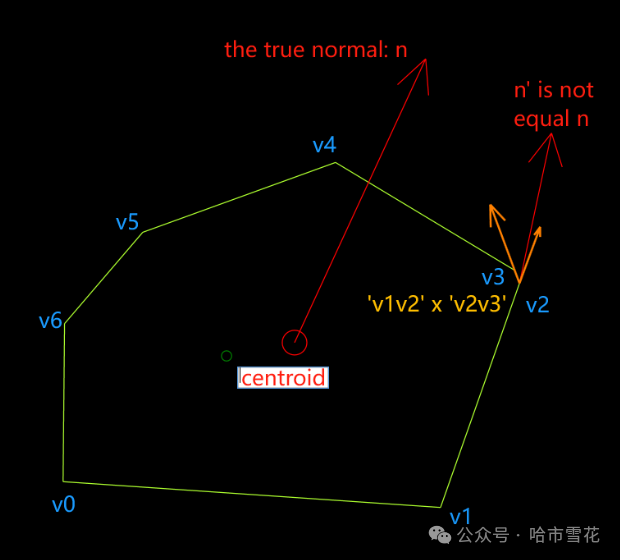
一种较好的办法是考虑所有边,即所有边参与运算,这将较大程度的对局部精度损失引起的误差进行“纠偏”。
提示
后续章节将涉及如何使法向量计算保持较高的精度。
3.任意多边形法向量
3.1.有向面积辅助法
在实际工程场景中,往往需要考虑任意多边形的情况,如实体参与布尔运算后存在不规则形状的面,需要计算面的法向量以正确的进行效果显示。
当多边形含有凹角时,运用上述“选择边与其后续邻接边进行叉乘”得到的法向量会是反向的,这时候我们不知道哪个是凹角,因为法向量还没有被正确的计算出来。这就需要一种通用的法向量计算方法。
补充
任意多边形法向量计算方案不止一种,如前文所述,本文将针对“轮廓有向面积辅助法”进行讲述,有关其他方法可联系作者或继续关注公众号文章。
从轮廓“正面”看向轮廓,轮廓是逆时针的,从轮廓“反面”看向轮廓,轮廓是顺时针的,轮廓的顺逆时针只是相对的,取决于怎么看向轮廓。
当轮廓法向朝向我们时,轮廓是逆时针的,这时轮廓有向面积为正,也就是从正面看,轮廓有向面积是正的。你可能大概有思路了,我们继续分析,
补充
基于轮廓正向法向量时,轮廓有向面积为正;基于轮廓反向法向量时,其面积为负。
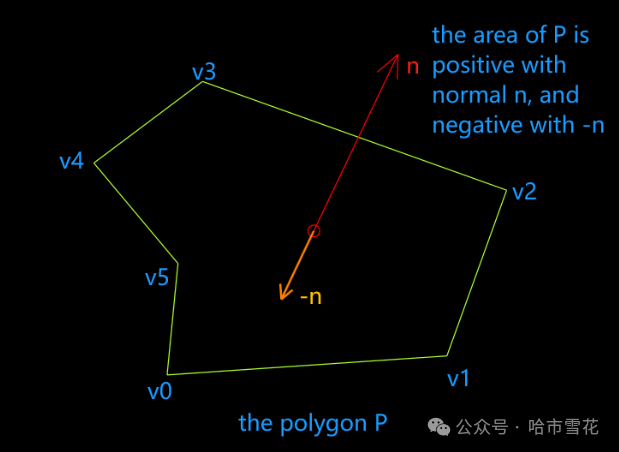
在不考虑正负的情况下,我们比较容易求得轮廓的法向量(可以运用“选择边与其后续邻接边进行叉乘”),然后基于此法向量进行轮廓面积计算,如果为正,则该法向量为正向法向量,如果面积为负,则该法向量为反向法向量,对其取反即得正向法向量。
提示
轮廓面积计算有多种方法,可以通过微积分方法或衍生的梯形投影和等方法,或采用Newell方法,详细可参考作者相关文章。
3.2.精度的提高
上文提到,由于浮点型存储和计算精度损失等原因,凸多边形上的点可能存在略微偏离所在平面,这时候参与运算的边如果恰好有非常短的边时,由其构造的相量与所在平面夹角将不为0,甚至偏离较大,这将导致求得的法向量存在较大的误差。
一种提高精度的思路是考虑所有相邻边得到的法向因素,进行加权平均,权重值为相邻边的夹角angle因素(弧度表示法),夹角在[0,PI/2)时取原值,在[PI/2,PI]时取PI-angle,因为在相同的条件下上述取值越大计算的精度越高,其对法向的贡献度越大,即权重值越大。
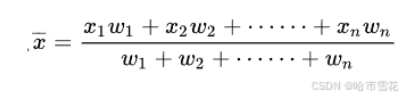
图:加权平均思想
提示
试想一下,当两条边无限接近于共线的情况,那么由它们计算得到的法向量无限接近于(0,0,0)。
仍然需要考虑凹凸角情况,统一将凹角或凸角计算得到的法向进行取反即可,因为符号会通过计算面积得到。一种实践是判断当前计算的法向是否与已计算过的法向存在夹角大于接近于PI值的情况(如PI/6*5,即150°),如果存在即取反,这样所有的法向被统一在面的一个方向了。
4.总结
对于特定规则的多边形,如三角形、凸多边形,计算法向量较为简单,可以运用“选择边与其后续邻接边进行叉乘”,但需要关注精度话题。
多边形有向面积与其法向量密切相关,对于任意多边形的法向量计算可以采用Newell法进行计算,公式简洁清晰,计算量较小,同时可保持较高的精度。
当然也可参考轮廓有向面积辅助法进行计算,同样可保持较高的精度,但其计算量相对Newell法较大。
-
图形几何之美系列:三维实体结构表达
-
图形几何之美系列:仿射变换矩阵
-
图形几何之美系列:仿射变换矩阵(二)
-
图形几何之美系列:仿射变换矩阵之先转后偏
-
图形几何之美系列:仿射变换矩阵之Y-Up和Z-Up
-
Unity动画:Hello World!
-
图形几何之美系列:面积计算之梯形投影求和
-
重磅发布:领略图形几何之美,向工业软件进击的小哈 #二维凸包
-
图形几何之美系列:法向量计算之轮廓有向面积辅助法
欢迎关注,图形几何之美系列 将继续更新......
相关文章:
图形几何之美系列:法向量计算之轮廓有向面积辅助法
“ 垂直于平面的直线所表示的向量为该平面的法向量,可以通过法向量识别平面正反面。法向量是轮廓或面的重要特征,求轮廓法向是一种基础的几何工具算法,在图形几何、图像处理等领域具有广泛的应用。” 图形几何之美系列:三维实体结…...

CPU的性能指标总结(学习笔记)
CPU 性能指标 我们先来回顾下,描述 CPU 的性能指标都有哪些。 首先,最容易想到的应该是 CPU 使用率,这也是实际环境中最常见的一个性能指标。 用户 CPU 使用率,包括用户态 CPU 使用率(user)和低优先级用…...

Cadence安装
记录一下安装过程,方便以后安装使用Cadence。 去吴川斌的博客下载安装包,吴川斌博客: https://www.mr-wu.cn/cadence-orcad-allegro-resource-downloads/ 下载阿狸狗破戒大师 我这边下载的是版本V3.2.6,同样在吴川斌的博客下载安装…...

【网络】子网掩码
> 作者:დ旧言~ > 座右铭:松树千年终是朽,槿花一日自为荣。 > 目标:了解什么是子网掩码,并且能熟练掌握子网掩码的相关计算。 > 毒鸡汤:有些事情,总是不明白,所以我不会…...

Android Osmdroid + 天地图 (二)
Osmdroid 天地图 (二) 前言正文一、定位监听二、改变地图中心三、添加Marker四、地图点击五、其他配置① 缩放控件② Marker更换图标③ 添加比例尺④ 添加指南针⑤ 添加经纬度网格线⑥ 启用旋转手势⑦ 添加小地图 六、源码 前言 上一篇中我们显示了地图…...

使用大语言模型创建 Graph 数据
Neo4j 是开源的 Graph 数据库,Graph 数据通过三元组进行表示,两个顶点一条边,从语意上可以理解为:主语、谓语和宾语。GraphDB 能够通过图来表达复杂的结构,非常适合存储知识型数据,本文将通过大语言实现图数…...
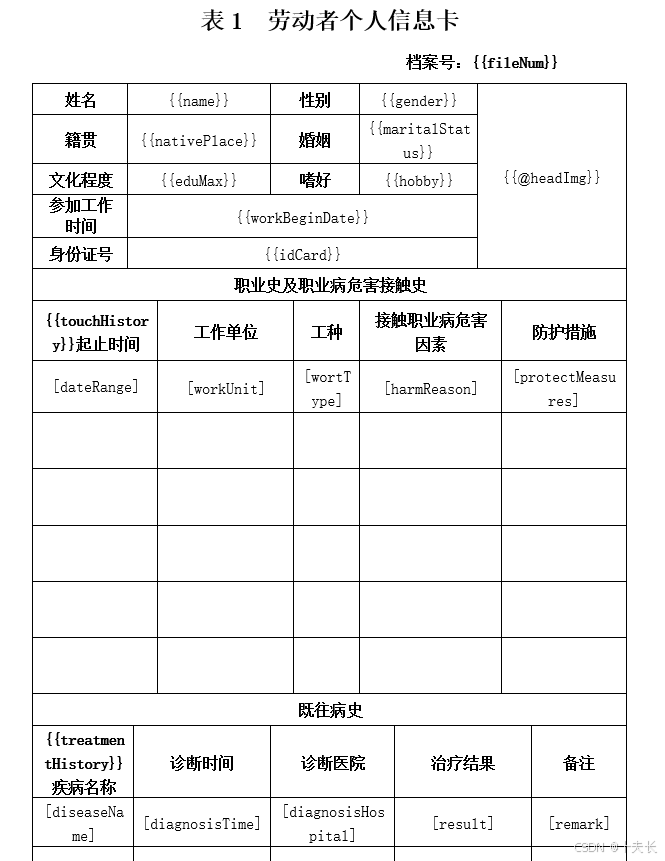
Java poi 模板导出Word 带图片
Java poi 模板导出Word 带图片 重点!!! 官方文档:https://deepoove.com/poi-tl/#_maven 最终效果 模板 其实内容都在官方文档里写的非常明白了 我这里只是抛砖引玉。 Maven依赖 <poi.version>4.1.2</poi.version>…...

SpringCloud-使用FFmpeg对视频压缩处理
在现代的视频处理系统中,压缩视频以减小存储空间、加快传输速度是一项非常重要的任务。FFmpeg作为一个强大的开源工具,广泛应用于音视频的处理,包括视频的压缩和格式转换等。本文将通过Java代码示例,向您展示如何使用FFmpeg进行视…...
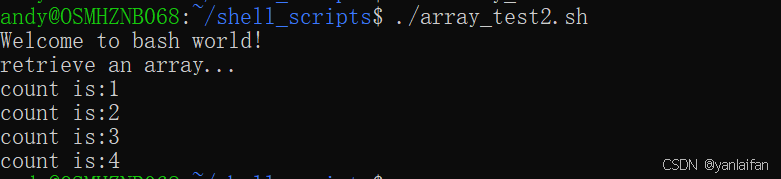
shell bash---类似数组类型
0 Preface/Foreword C/C,Python,Java等编程语言,都含有数组类型,那么shell脚本是不是也有类似的语法呢? 1 类似数组类型 1.1 ()类似数组类型 #! /bin/bashecho "Welcome to bash world!" anim…...
)
IIoT(Industrial Internet of Things,工业物联网)
IIoT(Industrial Internet of Things,工业物联网) 是指物联网技术在工业领域的应用。它将工业设备、传感器、控制系统、数据采集设备等通过互联网或局域网连接起来,实现设备的互联互通和智能化管理。IIoT的目标是提高工业生产效率…...
)
【C++】引用(reference)
引用是对一个变量或者对象取的别名 定义:真名的数据类型& 别名 真名; 既然是对一个变量或者对象取别名,那就得先有变量或对象,不能凭空取一个别名。也就是定义引用必须初始化。 对引用的操作和对引用对应的变量的操作是完全等价的引用…...

学习日记_20241115_聚类方法(层次聚类)
前言 提醒: 文章内容为方便作者自己后日复习与查阅而进行的书写与发布,其中引用内容都会使用链接表明出处(如有侵权问题,请及时联系)。 其中内容多为一次书写,缺少检查与订正,如有问题或其他拓展…...

安卓开发怎么获取返回上一级activity事件
在Android开发中,要获取返回上一级Activity的事件,通常是通过点击设备上的返回按钮或者在代码中调用finish()方法时触发的。为了处理这个事件,你可以在当前Activity中重写onBackPressed()方法。 以下是一个简单的例子: Override…...

神经网络与Transformer详解
一、模型就是一个数学公式 模型可以描述为:给定一组输入数据,经过一系列数学公式计算后,输出n个概率,分别代表该用户对话属于某分类的概率。 图中 a, b 就是模型的参数,a决定斜率,b决定截距。 二、神经网络的公式结构 举例:MNIST包含了70,000张手写数字的图像,其中…...

C语言之MakeFile
Makefile 的引入是为解决多文件项目中手动编译繁琐易错、缺乏自动化构建、项目管理维护困难以及跨平台构建不便等问题,实现自动化、规范化的项目构建与管理 MakeFile 简单的来说,MakeFile就是编写编译命令的文件 文件编写格式 目标:依赖文件列表 <Tab>命令列表…...

vue项目PC端和移动端实现在线预览docx、excel、pdf文件
可以参考vue-office官方github:GitHub - loonghe/vue-office: 支持word(.docx)、excel(.xlsx,.xls)、pdf等各类型office文件预览的vue组件集合,提供一站式office文件预览方案,支持vue2和3,也支持React等非Vue框架。…...
FlinkSql读取kafka数据流的方法(scala)
我的scala版本为2.12 <scala.binary.version>2.12</scala.binary.version> 我的Flink版本为1.13.6 <flink.version>1.13.6</flink.version> FlinkSql读取kafka数据流需要如下依赖: <dependency><groupId>org.apache.flink&…...

.NET 9 中 IFormFile 的详细使用讲解
在.NET应用程序中,处理文件上传是一个常见的需求。.NET 9 提供了 IFormFile 接口,它可以帮助我们轻松地处理来自客户端的文件上传。以下是 IFormFile 的详细使用讲解。 IFormFile 接口简介 IFormFile 是一个表示上传文件的接口,它提供了以下…...
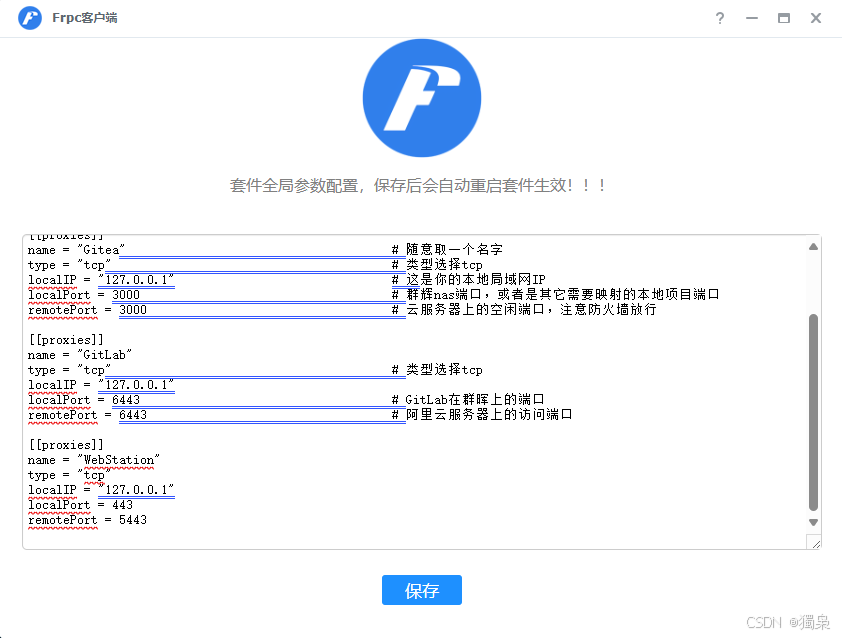
使用阿里云远程访问 Synology Web Station 的指南
使用阿里云远程访问 Synology Web Station 的指南 本文将指导如何通过阿里云服务器配置 Nginx 和 FRP,远程访问部署在 Synology NAS 上的 Web Station 服务,同时支持 HTTPS 安全访问。 背景 通过 Synology NAS 的 Web Station,可以部署 Wor…...

LlamaFactory介绍
目录 一、什么是LlamaFactory 1. 安装 LlamaFactory 2. 下载 LLaMA 模型 3. 运行 LLaMA 模型 4. 微调 LLaMA 模型 5. 优化本地运行 6. 推理加速 7. 硬件要求 二、总结 一、什么是LlamaFactory LlamaFactory 是一个用于训练和运行 LLaMA(Meta 的开源大型语言模型)模型…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...
