【SQL】E-R模型(实体-联系模型)
目录
一、介绍
1、实体集
定义和性质
属性
E-R图表示
2. 联系集
定义和性质
属性
E-R图表示
一、介绍
实体-联系数据模型(E-R数据模型)被开发来方便数据库的设计,它是通过允许定义代表数据库全局逻辑结构的企业模式(enterprise schema)来做到的。
E-R模型采用了三个基本概念:实体集、联系集和属性。
E-R模型还有一种相关联的图形表示:E-R图。
1、实体集
一个实体(entity)是现实世界中可区别与所有其他对象中的一个“事物”或“对象”。
例如,大学中的每个人都是一个实体。实体也可以是抽象的,比如课程或者航班预定。
定义和性质
实体集(entity set)是共享相同性质或属性、具有相同类型的实体的集合。
例如,一所给定大学的所有教师的集合可定义为instructor实体集,而不是指某个个别实体的特定集合。
实体集的外延(extension)指 属于实体集的实体的实际集合。因此,大学中教师的实际集合构成了instructor实体集的外延。
实体集不必互不相交。比如一个person实体可以是student实体,可以是instuctor实体。
属性
实体通过一组属性(attribute)来表示。
属性是实体集中每个成员所拥有的描述性性质。
为实体集设计一个属性表明数据库存储关于该实体集中每个实体的类似信息,但每个实体在每个属性上可以有它自己的值。
例如,instructor实体集可能具有的属性是ID、name,dept_name和salary.
在此,我们只考虑简单的属性---那些不能划分为子部分的属性。
每个实体在它的每个属性上都有一个值(value)。
E-R图表示
实体集在E-R图中用一个矩形表示,该矩阵分为两部分:实体集的名称,实体集所有属性的名称。

如图,E-R图显示的instructor和student实体集。
2. 联系集
定义和性质
联系(relationship)是多个实体间的相互关联。
比如,教师和学生的联系。
联系集(relationship set)是相同类型联系的集合。
联系集是在n>=2个(可能相同的)实体集上的数学关系。如果(E1,E2,....En)为实体集,那么联系集R是
{(e1,e2,...,en)| e1∈E1, e2∈E2,...., en∈En }
的一个子集,其中(e1,e2,...,en)是一个联系实例。
$$$ 实体集之间的关联被称为参与,即实体集(E1,E2,....En)参与(participate)联系集R。
属性
联系也可以具有被称作描述性属性(descriptive attribute)的属性。
E-R图表示
联系集在E-R图中用菱形表示,菱形通过线条连接到多个不同的实体集(矩形)。

显示advisor联系集的E-R图
联系集的属性在E-R图中通过未分割的矩形来表示。我们用虚线将此矩形与表示该联系集的菱形相连接。

将一个属性附加到联系集的E-R图
相关文章:

【SQL】E-R模型(实体-联系模型)
目录 一、介绍 1、实体集 定义和性质 属性 E-R图表示 2. 联系集 定义和性质 属性 E-R图表示 一、介绍 实体-联系数据模型(E-R数据模型)被开发来方便数据库的设计,它是通过允许定义代表数据库全局逻辑结构的企业模式…...

C/C++静态库引用过程中出现符号未定义的处理方式
问题背景: 在接入新库(静态库)时遇到了符号未定义问题,并发现改变静态库的链接顺序可以解决问题。 问题根源: 静态库是由 .o 文件拼接而成的,链接静态库时,链接器以 .o 文件为单位进行处理。链接…...

『VUE』27. 透传属性与inheritAttrs(详细图文注释)
目录 什么是透传属性(Forwarding Attributes)使用条件唯一根节点禁用透传属性继承总结 欢迎关注 『VUE』 专栏,持续更新中 欢迎关注 『VUE』 专栏,持续更新中 什么是透传属性(Forwarding Attributes) 在 V…...

借助Excel实现Word表格快速排序
实例需求:Word中的表格如下图所示,为了强化记忆,希望能够将表格内容随机排序,表格第一列仍然按照顺序编号,即编号不跟随表格行内容调整。 乱序之后的效果如下图所示(每次运行代码的结果都不一定相同&#x…...

数据结构 ——— 层序遍历链式二叉树
目录 链式二叉树示意图编辑 何为层序遍历 手搓一个链式二叉树 实现层序遍历链式二叉树 链式二叉树示意图 何为层序遍历 和前中后序遍历不同,前中后序遍历链式二叉树需要利用递归才能遍历 而层序遍历是非递归的形式,如上图:层序遍历的…...

使用 Prompt API 与您的对象聊天
tl;dr:GET、PUT、PROMPT。现在,可以使用新的 PromptObject API 仅使用自然语言对存储在 MinIO 上的对象进行总结、交谈和提问。在本文中,我们将探讨这个新 API 的一些用例以及代码示例。 赋予动机: 对象存储和 S3 API 的无处不在…...

SpringBoot整合Mybatis-Plus实践汇总
相关依赖 MyBatis-Plus涉及的依赖主要是Mybatis-start、和分页插件的依赖,不考虑使用额外分页插件的前提下,只需要mybatis-plus-boot-starter一个依赖即可与SpringBoot集成: <!--Mybatis-plugs--><dependency><groupId>co…...

基于Spring Boot的在线性格测试系统设计与实现(源码+定制+开发)智能性格测试与用户个性分析平台、在线心理测评系统的开发、性格测试与个性数据管理系统
博主介绍: ✌我是阿龙,一名专注于Java技术领域的程序员,全网拥有10W粉丝。作为CSDN特邀作者、博客专家、新星计划导师,我在计算机毕业设计开发方面积累了丰富的经验。同时,我也是掘金、华为云、阿里云、InfoQ等平台…...

Python实现人脸识别算法并封装为类库
引言 人脸识别技术在现代社会中应用广泛,从安全监控到智能门锁,再到社交媒体中的照片标记功能,都离不开这项技术。本文将详细介绍如何使用Python实现基本的人脸识别算法,并将其封装为一个类库,以便在多个项目中复用。…...

uniapp小程序分享使用canvas自定义绘制 vue3
使用混入结合canvas做小程序的分享 在混入里面定义一个全局共享的分享样式,在遇到特殊页面需要单独处理 utils/share.js import { ref } from vue; export default {onShow() {// 创建时设置统一页面的默认值uni.$mpShare {title: 分享的标题,path: /pages/home/…...

SpringCloud核心组件(四)
文章目录 NacosNacos 配置中心1.起源2.基本概念ProfileData IDGroup 3.基础配置a. bootstrap.ymlb. application.ymlc. nacos 中的配置 DataIDd.测试读取配置中心配置内容 4.配置隔离a.命名空间b.DataIDc.bootstrap.ymld.service 隔离 5.配置拆分a.配置拆分策略b.DataID 配置c.…...

如何把本地docker 镜像下载用到centos系统中呢?
如果需要将镜像下载到本地或在 CentOS 系统上使用该镜像,你可以按照以下步骤操作: 1. 拉取镜像 如果想将镜像从 Docker Hub 或其他镜像仓库下载到本地,可以使用 docker pull 命令。 如果使用的是本地构建的镜像(如 isc:v1.0.0&…...
Godot的开发框架应当是什么样子的?
目录 前言 全局协程还是实例协程? 存档! 全局管理类? UI框架? Godot中的异步(多线程)加载 Godot中的ScriptableObject 游戏流程思考 结语 前言 这是一篇杂谈,主要内容是对我…...

GitHub新手入门 - 从创建仓库到协作管理
GitHub新手入门 - 从创建仓库到协作管理 GitHub 是开发者的社交平台,同时也是代码托管的强大工具。无论是个人项目、开源协作,还是团队开发,GitHub 都能让你轻松管理代码、版本控制和团队协作。今天,我们将从基础开始,…...

作业25 深度搜索3
作业: #include <iostream> using namespace std; bool b[100][100]{0}; char map[100][100]{0}; int dx[4]{0,1,0,-1}; int dy[4]{1,0,-1,0}; int n,m; int sx,sy,ex,ey; int mink2147483647; void dfs(int,int,int); int main(){cin>>n>>m;for(…...

ubuntu20.04 colmap 安装2024.11最新
很多教程都很落后了,需要下载压缩包解压编译的很麻烦 现在就只需要apt install就可以了 apt更新 sudo apt update && sudo apt-get upgrade安装依赖 #安装依赖 sudo apt-get install git cmake ninja-build build-essential libboost-program-options-de…...
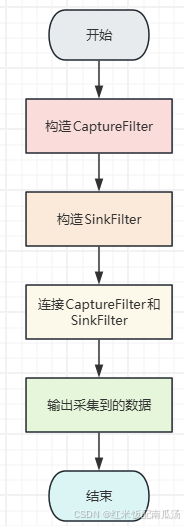
WebRTC视频 03 - 视频采集类 VideoCaptureDS 上篇
WebRTC视频 01 - 视频采集整体架构 WebRTC视频 02 - 视频采集类 VideoCaptureModule [WebRTC视频 03 - 视频采集类 VideoCaptureDS 上篇](本文) WebRTC视频 04 - 视频采集类 VideoCaptureDS 中篇 WebRTC视频 05 - 视频采集类 VideoCaptureDS 下篇 一、前…...
 详解)
python os.path.basename(获取路径中的文件名部分) 详解
os.path.basename 是 Python 的 os 模块中的一个函数,用于获取路径中的文件名部分。它会去掉路径中的目录部分,只返回最后的文件名或目录名。 以下是 os.path.basename 的详细解释和使用示例: 语法 os.path.basename(path) 参数 path&…...
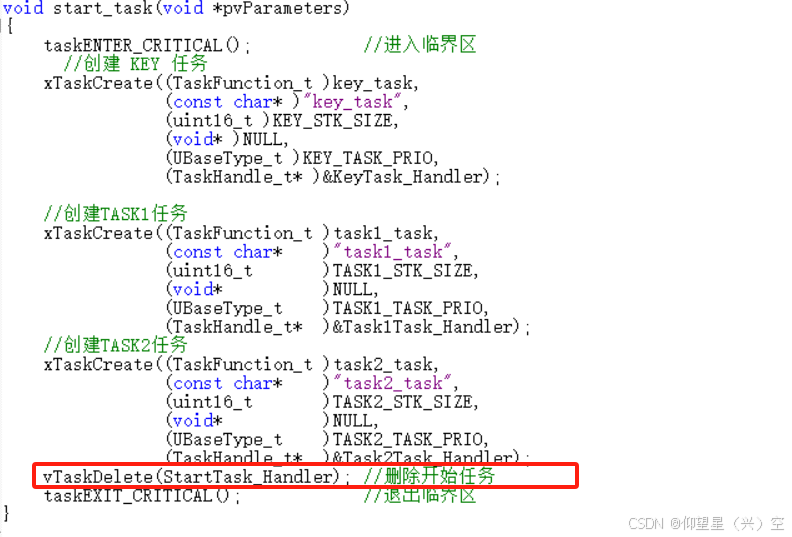
《FreeRTOS任务基础知识以及任务创建相关函数》
目录 1.FreeRTOS多任务系统与传统单片机单任务系统的区别 2.FreeRTOS中的任务(Task)介绍 2.1 任务特性 2.2 FreeRTOS中的任务状态 2.3 FreeRTOS中的任务优先级 2.4 在任务函数中退出 2.5 任务控制块和任务堆栈 2.5.1 任务控制块 2.5.2 任务堆栈…...

036集——查询CAD图元属性字段信息:窗体显示(CAD—C#二次开发入门)
提取CAD图元所有属性字段,通过窗体显示,效果如下:(curve改为entity) 代码如下: public void 属性查询() {List<Curve> ents Z.db.SelectEntities<Curve>();if (ents is null ||ents.Cou…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...

boost::filesystem::path文件路径使用详解和示例
boost::filesystem::path 是 Boost 库中用于跨平台操作文件路径的类,封装了路径的拼接、分割、提取、判断等常用功能。下面是对它的使用详解,包括常用接口与完整示例。 1. 引入头文件与命名空间 #include <boost/filesystem.hpp> namespace fs b…...
