数学分组求偶数和
问题描述
小M面对一组从 1 到 9 的数字,这些数字被分成多个小组,并从每个小组中选择一个数字组成一个新的数。目标是使得这个新数的各位数字之和为偶数。任务是计算出有多少种不同的分组和选择方法可以达到这一目标。
numbers: 一个由多个整数字符串组成的列表,每个字符串可以视为一个数字组。小M需要从每个数字组中选择一个数字。
例如对于[123, 456, 789],14个符合条件的数为:147 149 158 167 169 248 257 259 268 347 349 358 367 369。
测试样例
样例1:
输入:
numbers = [123, 456, 789]输出:14
样例2:
输入:
numbers = [123456789]输出:4
样例3:
输入:
numbers = [14329, 7568]输出:10
问题理解
- 输入:一个由多个整数字符串组成的列表
numbers,每个字符串代表一个数字组。 - 目标:从每个数字组中选择一个数字,组成一个新的数,使得这个新数的各位数字之和为偶数。
- 输出:计算出有多少种不同的分组和选择方法可以达到这一目标。
解题思路
-
数字和的奇偶性:
- 一个数的各位数字之和为偶数的条件是:所有选出的数字的和为偶数。
- 奇数 + 奇数 = 偶数
- 偶数 + 偶数 = 偶数
- 奇数 + 偶数 = 奇数
-
分组选择:
- 对于每个数字组,我们需要分别统计奇数和偶数的数量。
- 然后,我们需要计算出所有可能的组合,使得这些组合的和为偶数。
-
组合计算:
- 如果一个数字组中有
odd_count个奇数和even_count个偶数,那么我们可以从每个数字组中选择一个数字,使得最终的和为偶数。 - 具体来说,如果当前数字组中选择了奇数,那么下一个数字组中必须选择奇数(如果之前选择了奇数)或偶数(如果之前选择了偶数)。
- 如果一个数字组中有
关键步骤
- 统计奇数和偶数:对于每个数字组,统计奇数和偶数的数量。
- 组合计算:根据之前的选择情况,计算出当前数字组对总结果的贡献。
- 递归或动态规划:考虑使用递归或动态规划来计算所有可能的组合。
提示
- 你可以使用递归或动态规划来计算所有可能的组合。
- 考虑使用一个辅助函数来处理递归或动态规划的细节。
def solution(numbers):# 递归函数,用于计算所有可能的组合def count_combinations(index, current_sum):# 如果已经遍历完所有数字组if index == len(numbers):# 检查当前和是否为偶数return 1 if current_sum % 2 == 0 else 0# 初始化计数器count = 0# 遍历当前数字组中的每个数字for digit in numbers[index]:# 递归调用,计算下一个数字组的组合count += count_combinations(index + 1, current_sum + int(digit))return count# 将每个数字组转换为字符串列表numbers = [list(map(int, str(num))) for num in numbers]# 从第一个数字组开始递归计算return count_combinations(0, 0)if __name__ == "__main__":# 测试样例print(solution([123, 456, 789]))print(solution([123456789]))print(solution([14329, 7568]))
C#代码======================
using System;
using System.Collections.Generic;public class Solution
{public static int CountCombinations(List<string> numbers, int index, int currentSum){// 如果已经遍历完所有数字组if (index == numbers.Count){// 检查当前和是否为偶数return currentSum % 2 == 0 ? 1 : 0;}// 初始化计数器int count = 0;// 遍历当前数字组中的每个数字foreach (char digit in numbers[index]){// 递归调用,计算下一个数字组的组合count += CountCombinations(numbers, index + 1, currentSum + (digit - '0'));}return count;}public static int SolutionMethod(List<string> numbers){// 从第一个数字组开始递归计算return CountCombinations(numbers, 0, 0);}public static void Main(string[] args){// 测试样例Console.WriteLine(SolutionMethod(new List<string> { "123", "456", "789" }));Console.WriteLine(SolutionMethod(new List<string> { "123456789" }));Console.WriteLine(SolutionMethod(new List<string> { "14329", "7568" }) );}
}这里需要注意的是:
count += CountCombinations(numbers, index + 1, currentSum + (digit - '0'));中的 (digit - '0')
在C#中,字符(char)类型表示的是Unicode字符,而不是直接的数值。当你从一个字符中提取数值时,你需要将其转换为对应的整数值。
在C#中,字符 '0' 到 '9' 的ASCII值分别是48到57。因此,如果你有一个字符 '5',它的ASCII值是53。为了得到对应的数值5,你需要从53中减去48(即 '0' 的ASCII值)。
具体解释
digit是一个字符,例如'5'。digit - '0'实际上是'5' - '0',即53 - 48,结果是5。
这样,我们就可以将字符 '5' 转换为整数 5。
char digit = '5';
int number = digit - '0'; // 结果是 5 
相关文章:

数学分组求偶数和
问题描述 小M面对一组从 1 到 9 的数字,这些数字被分成多个小组,并从每个小组中选择一个数字组成一个新的数。目标是使得这个新数的各位数字之和为偶数。任务是计算出有多少种不同的分组和选择方法可以达到这一目标。 numbers: 一个由多个整数字符串组…...

机器学习基础02_特征工程
目录 一、概念 二、API 三、DictVectorize字典列表特征提取 四、CountVectorize文本特征提取 五、TF-IDF文本1特征词的重要程度特征提取 六、无量纲化预处理 1、MinMaxScaler 归一化 2、StandardScaler 标准化 七、特征降维 1、特征选择 VarianceThreshold 底方差…...

CSS Modules中的 :global
最近写需求遇到如下代码,我们来分析一番: .medicine-bot {:global(.cosd-site-vcard-card) {margin-top: -3px;}:global(.cosd-site-vcard-title-text) {font-size: var(--cos-text-headline-sm);}:global(.cosd-site-vcard-button) {background-color: …...

linux病毒编写+vim shell编程
学习视频来自B站UP主泷羽sec,如涉及侵权马上删除文章 感谢泷羽sec 团队的教学 请一定遵循《网络空间安全法》!!! Linux目录介绍 /bin 二进制可执行文件(kali里面是工具一些文件)/etc 系统的管理和配置文…...

WinDefender Weaker
PPL Windows Vista / Server 2008引入 了受保护进程的概念,其目的不是保护您的数据或凭据。其最初目标是保护媒体内容并符合DRM (数字版权管理)要求。Microsoft开发了此机制,以便您的媒体播放器可以读取例如蓝光,同时…...
)
智能工厂的设计软件 为了监管控一体化的全能Supervisor 的监督学习 之 序5 架构for认知系统 总述 (架构全图)
本文提要 本文讨论的“智能工厂的设计软件” for认知系统的架构全图 ,这有别于前面所说的“智能工厂的设计软件”的“全景图”。两者在内容和侧重点上有所不同,但它们共同构成了对智能工厂设计软件的全面描述。 全景图是对智能工厂设计软件的整体概览&…...

vmware集群 vSAN HCL 数据库
HCL数据库升级 https://partnerweb.vmware.com/service/vsan/all.json VSAN版本目录升级 https://vcsa.vmware.com/ph/api/v1/results?deploymentId2d02e861-7e93-4954-9a73-b08692a330d1&collectorIdVsanCloudHealth.6_5&objectId0c3e9009-ba5d-4e5f6-bae8-f25ec5…...

人工智能引发直播革命:AI 技术塑造无人直播全新体验
在数字化浪潮席卷全球的今天,人工智能(AI)技术以其无与伦比的速度和广度,正深刻地改变着各行各业的面貌。其中,直播行业作为新媒体时代的宠儿,也迎来了由AI技术引领的颠覆性变革。这场由人工智能引发的直播…...

数据研发基础 | 什么是流批一体
流批一体的概念是可能出现在大厂的面试题中的,虽然就算大厂实习也没机会实操这样的高级操作,学一点概念,面试多少是能说上一两句的。大致就是希望一套代码能同时在批处理和流处理中运行(同时做离线计算和实时计算)。下…...

《Python网络安全项目实战》项目6 编写密码工具程序
《Python网络安全项目实战》项目6 编写密码工具程序 项目6 编写密码工具程序任务6.1 猜数字游戏任务描述任务分析任务实施6.1.1 编写基本的猜数字程序6.1.3 测试并修改程序6.1.4 给程序增加注释 任务拓展任务实施6.2.1 生成随机密码6.2.4 菜单功能 相关知识1. 密码字典2. 密码字…...

现代C++HTTP框架cinatra
文章目录 cinatra简介主要特点 快速上手编译器版本要求使用指南快速示例 项目地址 cinatra简介 cinatra是一个基于C20协程的高性能HTTP框架,它的目标是提供一个快速开发的C HTTP框架解决方案 它不仅支持HTTP/1.1和1.0,还支持SSL和WebSocket,…...
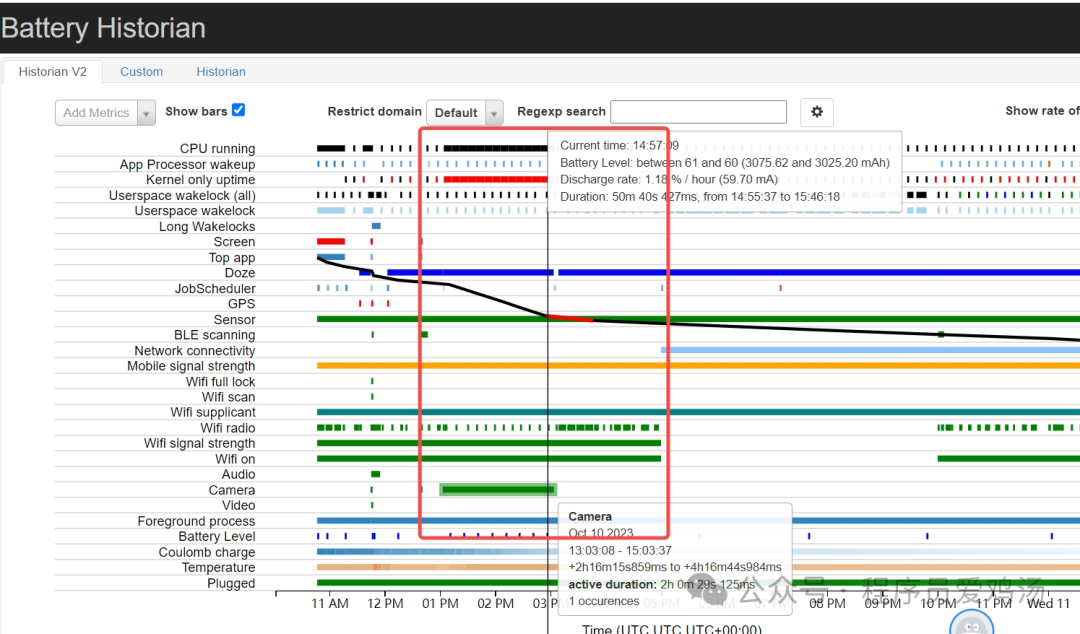
【功耗现象】com.gorgeous.lite后台Camera 使用2小时平均电流200mA耗电量400mAh现象
现象 轻颜相机(com.gorgeous.lite)后台Camera 使用2小时平均电流200mA(BugReport提供的电流参考数据),耗电量400mAh 即耗电占比(200mA*2h)/(12.83h*52.68mA )400mAh/623mAh62% CameraOct 10 202321:03:08 - 23:03:372h16m15s859ms to 4h16m44s984msactive duration: 2h 0m 29…...

06.VSCODE:备战大项目,CMake专项配置
娇小灵活的简捷配置不过是年轻人谈情说爱的玩具,帝国大厦的构建,终归要交给CMake去母仪天下。一个没有使用 CMake 的 C 项目,就像未来世界里的一台相声表演,有了德纲却无谦,观众笑着遗憾。—— 语出《双城记》作者&…...

还是小时候味道的麻辣片
麻辣片的诞生,源于人们对辣味的热爱和对丰富口感的追求。它将辣椒的火辣、香料的浓郁和豆制品的醇厚完美结合在一起,创造出了一种令人回味无穷的美食体验。无论是在学校的小卖部、街头的小吃摊,还是超市的货架上,麻辣片都以其鲜艳…...

GaussDB部署架构
GaussDB部署架构 云数据库GaussDB管理平台(TPOPS)基于B/S架构开发,由Web、管控Service、管控Agent三部分组成,软件结构如图1所示。 图1 各节点部署架构 Web:作为用户接入子系统,用于将用户在Web下发的操作…...
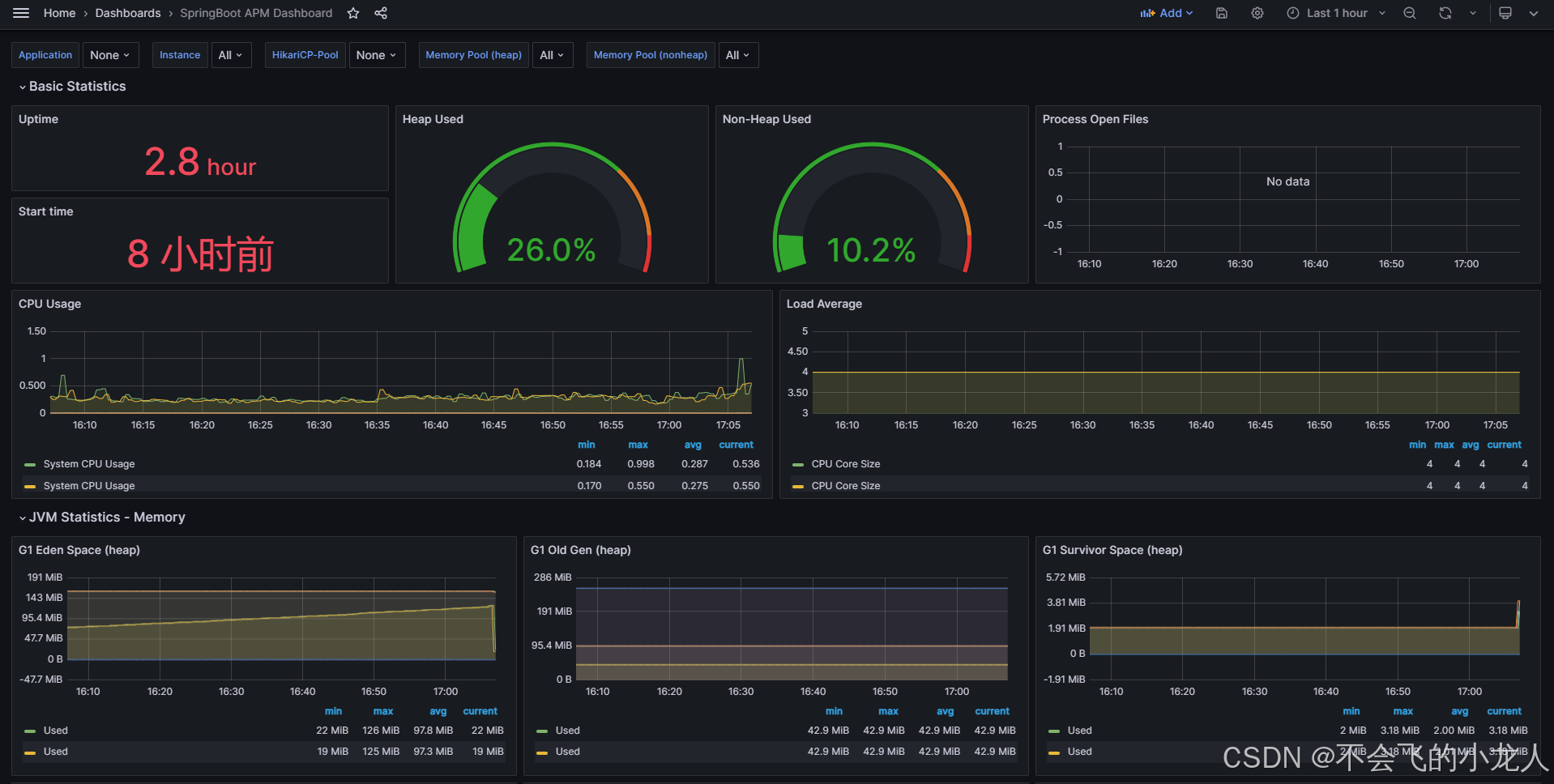
遥测数据采集工具Grafana Alloy
介绍 Alloy是Grafana产品公司旗下的一款新主推遥测数据采集工具,Grafana Alloy也是一个开源OpenTelemetry收集器,具有内置 Prometheus管道并支持指标、日志、跟踪和配置文件。Alloy支持为OTEL、Prometheus、Pyroscope、Loki等服务提供许多指标、日志、跟…...
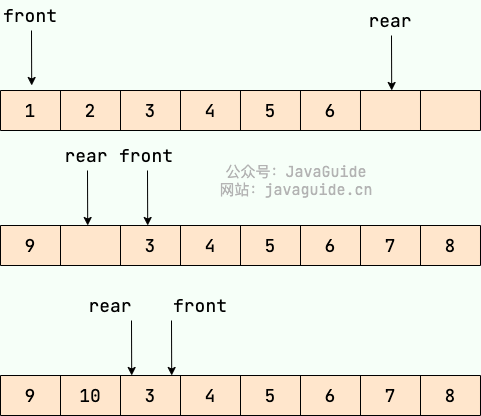
线性数据结构
数组 数组(Array) 是一种很常见的数据结构。它由相同类型的元素(element)组成,并且是使用一块连续的内存来存储。 我们直接可以利用元素的索引(index)可以计算出该元素对应的存储地址。 数组…...

【ArcGIS微课1000例】0127:计算城市之间的距离
本文讲述,在ArcGIS中,计算城市(以地级城市为例)之间的距离,效果如下图所示: 一、数据准备 加载配套实验数据包中的地级市和行政区划矢量数据(订阅专栏后,从私信查收数据),如下图所示: 二、计算距离 1. 计算邻近表 ArcGIS提供了计算点和另外点之间距离的工具:分析…...

【算法】二分
1. 找到有序区间中 x 最左边的数字的位置 static int getL(int a[], int l, int r, int x) {while (l < r) {int mid l r >> 1;if (x < a[mid]) {r mid;} else {l mid 1;}}if (a[l] ! x) return -1;return l;} 2. 找到有序区间中 x 最右边的数字的位置 stati…...

ARM CCA机密计算安全模型之简介
安全之安全(security)博客目录导读 目录 1、引言 2、问题陈述 3、CCA 安全保证 3.1 对领域所有者的安全保证 3.2 对host环境的安全保证 Arm 机密计算架构(CCA)安全模型(SM)定义了 CCA 隔离架构的安全要求和基本安全属性。这…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...
