LeetCode题解:17.电话号码的数字组合【Python题解超详细,回溯法、多叉树】,知识拓展:深度优先搜索与广度优先搜索
题目描述
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。

示例 1:
输入:digits = "23" 输出:["ad","ae","af","bd","be","bf","cd","ce","cf"]
示例 2:
输入:digits = "" 输出:[]
示例 3:
输入:digits = "2" 输出:["a","b","c"]
解答
class Solution(object):def letterCombinations(self, digits):""":type digits: str:rtype: List[str]"""# 思路一:回溯法# 对于digit为空的特殊情况,直接返回[]if not digits:return []# 定义数字与字母映射的字典phone_map = {'2': 'abc', '3': 'def', '4': 'ghi', '5': 'jkl','6': 'mno', '7': 'pqrs', '8': 'tuv', '9': 'wxyz'}# 定义回溯函数# combination:当前已经生成的组合# nextdigits:剩余未处理的数字def backtract(combination,nextdigits):# 如果没有剩余数字,则读入combination并停止if len(nextdigits)==0:output.append(combination)return # 遍历当前数字对应的所有字母,进入下一阶段for letter in phone_map[nextdigits[0]]:# 将当前字母加入组合,并递归处理剩余数字backtract(combination+letter,nextdigits[1:])# 输出字典output=[]# 初始化回溯函数backtract("",digits)return output# # 思路二:构建多叉树# # 对于特殊情况,直接输出[]# if not digits:# return []# # 定义数字与字母映射的字典# phone_map = {'2': 'abc', '3': 'def', '4': 'ghi', '5': 'jkl','6': 'mno', '7': 'pqrs', '8': 'tuv', '9': 'wxyz'}# # 定义深度优先搜索(DFS)函数# # node:当前数字对应的字母映射# # path:当前路径,即已生成的部分组合# def dfs(node,path):# # 如果路径长度等于输入数字长度,表示生成了一个完整组合# if len(path)==len(digits):# output.append(path)# return# # 如果当前节点为空,直接返回(无效分支)# if node is None:# return# # 遍历当前数字对应的所有字母# for letter in phone_map[node]:# dfs(digits[len(path) + 1] if len(path) + 1 < len(digits) else None,path+letter)# output=[]# dfs(digits[0],"")# return output
思路一,回溯法:其核心思想是逐步生成所有可能的字母组合,通过递归遍历当前数字对应的所有字母,并将当前字母加入到已经生成的部分组合中。当没有剩余数字时,将完整的组合加入结果列表。这种方法的优点是逻辑清晰,容易实现递归树的分支剪枝。
思路二,多叉树的深度优先搜索:通过构造一棵树,每个数字的字母映射为一层,路径上的节点代表当前生成的组合。通过递归从顶层到叶子节点(即完成一个完整组合)逐层搜索,并将完整的路径加入结果列表。这种方法本质上也是通过递归实现,但更侧重于以树的结构来思考问题。相比回溯法,逻辑上稍复杂,但仍能很好地生成所有组合。
对比两种方法,回溯法以 "递归 + 剪枝" 的方式,通过遍历每个数字的字母映射生成组合,逻辑简洁明了,易于实现;多叉树的 DFS则从树的结构出发,递归生成字母组合,逻辑上与回溯法类似,但代码中显示了树的层级关系,适合对树结构有直观理解的场景。并且,两种方法在时间复杂度上相同,均为 O(()
n 为包含3个字母的数字数量,m 为包含4个字母的数字数量)。
知识拓展:深度优先搜索 vs. 广度优先搜索
深度优先搜索(Depth-First Search, DFS)
概念
深度优先搜索是一种搜索策略,它会沿着一个路径不断深入到树或图的叶子节点,直到不能再继续深入为止,然后回溯到上一个分支点继续探索其他路径。它优先关注的是路径的深度。
核心特点
- 深入探索:优先沿着路径一直深入到底。
- 回溯机制:在某路径不能继续深入时,回到上一个分支点继续探索。
- 使用栈结构:可以用递归(隐式栈)或显式栈实现。
A/ \B C/ \
D E# 其邻接表的结构如下:
graph = {'A': ['B', 'C'],'B': ['D', 'E'],'C': ['F'],'D': [],'E': [],'F': []
}
以图中的搜索为例,假设我们从节点 A 出发,目标是访问所有节点,则深度优先的访问顺序为:A → B → D → E → C,其搜索过程如下:
- 从
A出发,访问B。 - 从
B深入到D,访问D。 - 从
D回溯到B,然后访问E。 - 从
B回溯到A,然后访问C。
实现(递归版本)
def dfs(node, visited):if node in visited: # 如果节点已访问过,直接返回returnvisited.add(node) # 标记当前节点为已访问print(node) # 访问当前节点for neighbor in graph[node]: # 遍历临接表中的相邻节点dfs(neighbor, visited)
广度优先搜索(Breadth-First Search, BFS)
概念
广度优先搜索是一种搜索策略,它从起始节点开始,按照层次逐层向外扩展,直到找到目标或访问完所有节点。它优先关注的是路径的宽度。
核心特点
- 逐层探索:先访问当前层的所有节点,再访问下一层的节点。
- 使用队列结构:通过队列(FIFO)存储待访问的节点。
A/ \B C/ \
D E 还是以同样的图为例,从节点 A 出发,其访问顺序为: A → B → C → D → E,其搜索过程如下:
- 从
A出发,访问A。 - 访问
A的所有直接相邻节点:B和C。 - 访问
B的相邻节点:D和E。
实现
from collections import dequedef bfs(start):queue = deque([start]) # 初始化队列visited = set() # 用于存储已访问的节点while queue:node = queue.popleft() # 从队列头部取出一个节点if node not in visited:visited.add(node) # 标记为已访问print(node) # 访问当前节点queue.extend(graph[node]) # 将相邻节点加入队列
两者对比
| 属性 | 深度优先搜索 (DFS) | 广度优先搜索 (BFS) |
| 搜索策略 | 一条路径深入到底,无法继续时回溯。 | 按层次逐层搜索,每层节点按宽度扩展。 |
| 数据结构 | 栈(递归或显式栈)。 | 队列(FIFO)。 |
| 适用场景 | 适用于寻找深度路径,如迷宫寻路问题。 | 适用于寻找最短路径,如图的最短路径问题。 |
| 时间复杂度 | O(V+E),其中 V 是顶点数,E 是边数。 | O(V+E),与 DFS 相同。 |
| 空间复杂度 | 最坏情况下需要存储所有递归栈帧。 | 需要存储整个图的一层节点。 |
| 实现难度 | 易于实现,递归实现尤为简单。 | 需要显式维护队列,相对复杂一些。 |
感谢阅读,希望对你有所帮助~
相关文章:
LeetCode题解:17.电话号码的数字组合【Python题解超详细,回溯法、多叉树】,知识拓展:深度优先搜索与广度优先搜索
题目描述 给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。 示例 1: 输入:digits "23" 输出…...

《JVM第10课》内存溢出(OOM)排查过程
文章目录 常用命令1. jps2. jconsole3. jstat4. jmap 工具1.jvisualvm 排查OOM的方法其实很简单很简单。 如果能找到拋OOM的日志,可以在日志里看到是哪一行抛出的OOM异常。如果找不到日志,那么处理方式是导出Java进程的内存快照,然后用工具查…...

Thinkphp6视图介绍
一.MVC MVC 软件系统分为三个基本部分:模型(Model)、视图(View)和控制器(Controller) ThinkPHP6 是一个典型的 MVC 架构 控制器—控制器,用于将用户请求转发给相应的Model进行处理&a…...
)
躺平成长-人工智能进行编程-(12)
躺平成长: 让每一个人在科技(开源的网络/智能科技对于生活琐事的处理)的帮助下,实现养生反卷,躺平成长。 开源竞争: 当你无法彻底掌握技术的时候,你就开源这个技术,形成技术依赖&a…...
计算机网络中的域名系统(DNS)及其优化技术
💓 博客主页:瑕疵的CSDN主页 📝 Gitee主页:瑕疵的gitee主页 ⏩ 文章专栏:《热点资讯》 计算机网络中的域名系统(DNS)及其优化技术 计算机网络中的域名系统(DNS)及其优化…...
函数的用法)
Matplotlib库中show()函数的用法
在Matplotlib库中使用show()函数是用于显示绘制的图形的函数。它将图形显示在屏幕上或保存到文件中。show()函数通常在绘制完图形后调用。 Matplotlib是一个用于绘制2D图形的Python库,它提供了丰富的绘图工具和函数,可以用于创建各种类型的图表…...

C#中object和dynamic
在C#中,object和dynamic都是用于存储不同类型值的类型,但它们之间存在一些关键的区别: object object是C#中的基元类型之一,是所有其他类型的最终基类。当你将一个值赋给object类型的变量时,编译器会执行装箱操作&am…...

Spring Cloud Eureka 服务注册与发现
Spring Cloud Eureka 服务注册与发现 一、Eureka基础知识概述1.Eureka两个核心组件2.Eureka 服务注册与发现 二、Eureka单机搭建三、Eureka集群搭建四、心跳续约五、Eureka自我保护机制 一、Eureka基础知识概述 1.Eureka两个核心组件 Eureka Server :服务注册中心…...

【WPF】Prism学习(三)
Prism Commands 1.复合命令(Composite Commanding) 这段内容主要介绍了在应用程序中如何使用复合命令(Composite Commands)来实现多个视图模型(ViewModels)上的命令。以下是对这段内容的解释: …...

1+X应急响应(网络)系统加固:
系统加固: 数据库的重要性: 数据库面临的风险: 数据库加固: 业务系统加固: 安全设备加固: 网络设备加固:...

使用 Grafana api 查询 Datasource 数据
一、使用grafana 的api 接口 官方API 二、生成Api key 点击 Administration -》Users and accss -》Service accounts 进入页面 点击Add service account 创建 service account 点击Add service account token 点击 Generate token , 就可以生成 api key 了 三、进入grafana…...

【电子设计】按键LED控制与FreeRTOS
1. 安装Keilv5 打开野火资料,寻找软件包 解压后得到的信息 百度网盘 请输入提取码 提取码:gfpp 安装526或者533版本都可以 下载需要的 F1、F4、F7、H7 名字的 DFP pack 芯片包 安装完 keil 后直接双击安装 注册操作,解压注册文件夹后根据里面的图示步骤操作 打开说明 STM…...
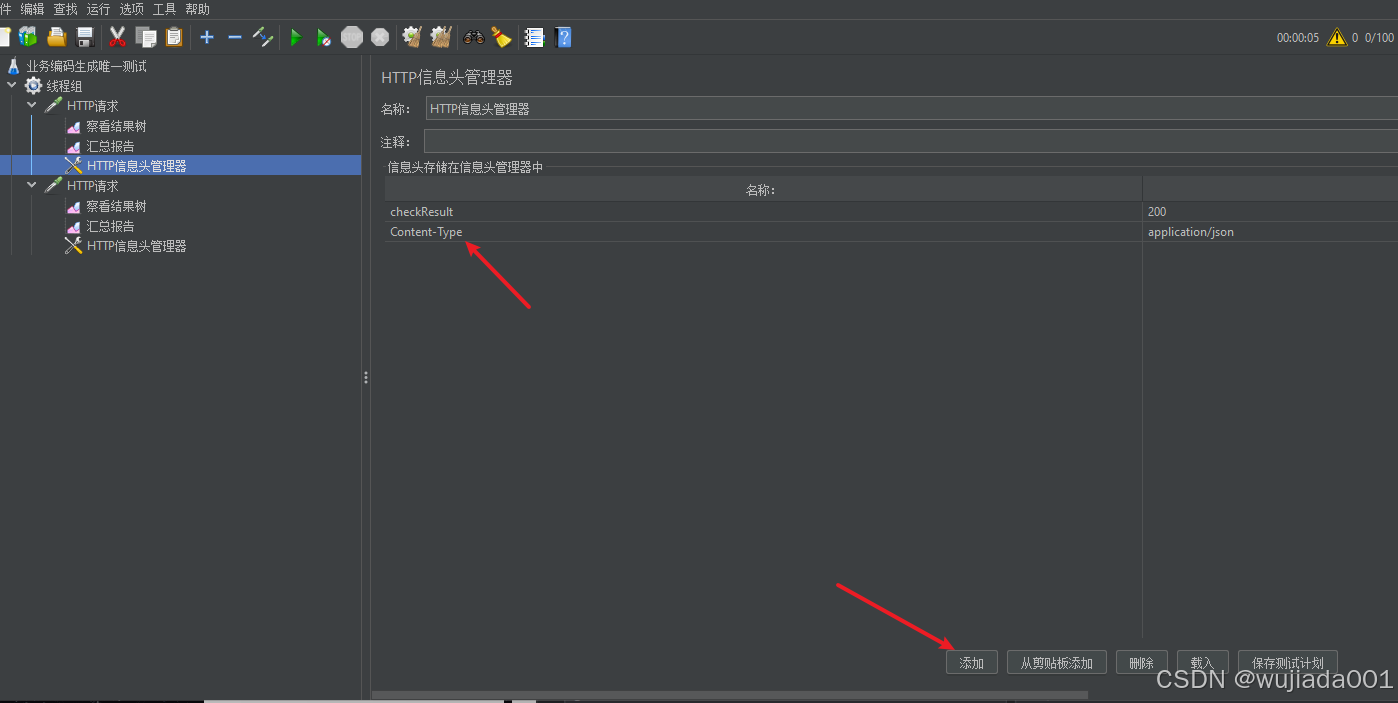
JMeter中添加请求头
在JMeter中添加请求头的步骤如下: 1.打开HTTP信息头管理器 : 首先,你需要进入JMeter的HTTP请求组件。这可以通过在HTTP请求测试元素上右键点击,然后选择“添加 > 配置元件 > HTTP信息头管理器”来完成。 2.添加新的请求头…...

VMD + CEEMDAN 二次分解,CNN-LSTM预测模型
往期精彩内容: 时序预测:LSTM、ARIMA、Holt-Winters、SARIMA模型的分析与比较 全是干货 | 数据集、学习资料、建模资源分享! EMD变体分解效果最好算法——CEEMDAN(五)-CSDN博客 拒绝信息泄露!VMD滚动分…...

【Linux系统编程】第四十六弹---线程同步与生产消费模型深度解析
✨个人主页: 熬夜学编程的小林 💗系列专栏: 【C语言详解】 【数据结构详解】【C详解】【Linux系统编程】 目录 1、Linux线程同步 1.1、同步概念与竞态条件 1.2、条件变量 1.2.1、认识条件变量接口 1.2.2、举例子认识条件变量 1.2.3、…...

VoIP是什么?
IP 语音 (VoIP)(Voice over Internet Protocol) 是一种通过互联网拨打电话的方法。与旧的固定电话系统不同,互联网并非设计用于在连接的人之间实时传输音频信号。必须构建专门的技术和协议才能使之成为可能,这些技术和协议构成了 …...

MySQL 中的集群部署方案
文章目录 MySQL 中的集群部署方案MySQL ReplicationMySQL Group ReplicationInnoDB ClusterInnoDB ClusterSetInnoDB ReplicaSetMMMMHAGalera ClusterMySQL ClusterMySQL Fabric 总结参考 MySQL 中的集群部署方案 MySQL Replication MySQL Replication 是官方提供的主从同步方…...

《设计模式》创建型模式总结
目录 创建型模式概述 Factory Method: 唯一的类创建型模式 Abstract Factory Builder模式 Prototype模式 Singleton模式 最近在参与一个量化交易系统的项目,里面涉及到用java来重构部分vnpy的开源框架,因为是框架的搭建,所以会涉及到像…...

Conda安装与使用中的若干问题记录
Conda安装与使用中的若干问题记录 1.Anaconda 安装失败1.1.问题复述1.2.问题解决(安装建议) 2.虚拟环境pip install未安装至本虚拟环境2.1.问题复述2.2.问题解决 3.待补充 最近由于工作上的原因,要使用到Conda进行虚拟环境的管理,…...

人力资源招聘系统的革新之路:从传统到智能的转变
在全球化与数字化交织的今天,企业间的竞争日益激烈,而人才作为企业发展的核心驱动力,其重要性不言而喻。传统的人力资源招聘方式,如依赖纸质简历、人工筛选、面对面面试等,不仅效率低下,且难以精准匹配企业…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...
