AtCoder Beginner Contest 380(A-F)
比赛链接:AtCoder Beginner Contest 380(A-F)
A - 123233
题意
给出一个数字 N N N,问这个数字中是否 1 1 1 恰好出现了 1 1 1 次, 2 2 2 恰好出现了 2 2 2 次, 3 3 3 恰好出现了 3 3 3 次。
数据范围
100000 ≤ N ≤ 999999 100000 \le N \le 999999 100000≤N≤999999
思路
把 N N N 当字符串处理,然后直接遍历字符串,统计每种数字的数量,判断是否符合条件即可
复杂度
时间复杂度 O ( ∣ N ∣ ) O(|N|) O(∣N∣),空间复杂度 O ( ∣ N ∣ ) O(|N|) O(∣N∣)
代码实现
// Problem: A - 123233
// Contest: AtCoder - AtCoder Beginner Contest 380
// URL: https://atcoder.jp/contests/abc380/tasks/abc380_a
// Memory Limit: 1024 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;#define int long longconst int N = 1e6 + 5;void solve()
{string s;cin >> s;int cnt[10] = { 0 };for (char c : s) {cnt[c - '0']++;}if (cnt[1] == 1 && cnt[2] == 2 && cnt[3] == 3)cout << "Yes";elsecout << "No";
}signed main()
{ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);int T = 1;// cin >> T;while (T--) {solve();}
}
B - Hurdle Parsing
题意
有一个长度为 n n n 的序列 A A A,通过序列 A A A 以如下方式构造出字符串 S S S。
- S S S 以 ′ ∣ ′ '|' ′∣′ 开头。 然后进行 n n n 次操作:
- 在第 i i i 次操作时,添加 A i A_i Ai 个 ′ − ′ '-' ′−′ 到 S S S
结尾,然后添加 ′ ∣ ′ '|' ′∣′ 到 S S S 结尾。
现在给出字符串 S S S,求出序列 A A A。
数据范围
3 ≤ ∣ S ∣ ≤ 100 , n ≥ 1 3\le |S| \le 100,n \ge 1 3≤∣S∣≤100,n≥1
思路
A i A_i Ai 为 S S S 中第 i i i 个字符 ′ − ′ '-' ′−′ 的连续段的长度,因此可以从左到右遍历 S S S,每遇到一个字符 ′ − ′ '-' ′−′,就以该字符为开头,向右遍历完其所在的连续段,从而得到该连续段的长度。
在遍历完一个连续段后,就直接跳到连续段之后的下一个位置遍历,这样就可以遍历到所有的连续段并得到对应长度。
复杂度
时间复杂度 O ( ∣ S ∣ ) O(|S|) O(∣S∣),空间复杂度 O ( ∣ S ∣ ) O(|S|) O(∣S∣)
代码实现
// Problem: B - Hurdle Parsing
// Contest: AtCoder - AtCoder Beginner Contest 380
// URL: https://atcoder.jp/contests/abc380/tasks/abc380_b
// Memory Limit: 1024 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;#define int long longconst int N = 1e6 + 5;void solve()
{string s;cin >> s;int n = s.size();for (int i = 0; i < n; i++) {if (s[i] == '-') {int j = i;while (j < n && s[j] == '-')j++;cout << j - i << ' ';i = j - 1;}}
}signed main()
{ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);int T = 1;// cin >> T;while (T--) {solve();}
}
C - Move Segment
题意
给出一个长度为 n n n 的 01 01 01 串 S S S。
定义 ′ 1 − b l o c k ′ '1-block' ′1−block′ 为只含 1 1 1 的子串,且该子串前后都不存在 1 1 1,换句话说,若子串对应的区间为 [ l , r ] [l,r] [l,r],则 l = 1 l=1 l=1 或 S l − 1 = 0 S_{l-1} = 0 Sl−1=0,且 r = n r = n r=n 或 S r + 1 = 0 S_{r+1} = 0 Sr+1=0。
01 01 01 串中保证至少有 k k k 个 ′ 1 − b l o c k ′ '1-block' ′1−block′,现在要求把第 k k k 个 ′ 1 − b l o c k ′ '1-block' ′1−block′ 移动到 第 k − 1 k-1 k−1 个 ′ 1 − b l o c k ′ '1-block' ′1−block′ 的后面,然后输出修改后的 S S S。
数据范围
1 ≤ n ≤ 5 ∗ 1 0 5 , 2 ≤ k 1 \le n \le 5*10^5,2 \le k 1≤n≤5∗105,2≤k
思路
模拟题,从左到右遍历字符串,然后记录上一个 ′ 1 − b l o c k ′ '1-block' ′1−block′ 的末尾下标 p r e pre pre,当遍历到第 k k k 个 ′ 1 − b l o c k ′ '1-block' ′1−block′ 时,将其移动到 p r e pre pre 接下去的位置即可。
复杂度
时间复杂度 O ( n ) O(n) O(n),空间复杂度 O ( n ) O(n) O(n)
代码实现
// Problem: C - Move Segment
// Contest: AtCoder - AtCoder Beginner Contest 380
// URL: https://atcoder.jp/contests/abc380/tasks/abc380_c
// Memory Limit: 1024 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;#define int long longconst int N = 1e6 + 5;int n, k;
string s;void solve()
{cin >> n >> k >> s;int pre = -1, cnt = 0;for (int i = 0; i < n; i++) {if (s[i] == '1') {cnt++;int j = i;while (j < n && s[j] == '1') {j++;}if (cnt == k) {int len = j - i;for (int i1 = 1; i1 <= len; i1++) {s[i + i1 - 1] = '0';}for (int i1 = 1; i1 <= len; i1++) {s[pre + i1] = '1';}break;}pre = i = j - 1;}}cout << s;
}signed main()
{ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);int T = 1;// cin >> T;while (T--) {solve();}
}
D - Strange Mirroring
题意
给出一个字符串 S S S,对 S S S 进行 1 0 100 10^{100} 10100 次如下操作:
-
新建一个字符串 T T T,通过转换 S S S 每个位置的字母的大小写得到。
-
把 S S S 变成 S + T S+T S+T。
现在进行 q q q 次查询,第 i i i 次查询给出一个数字 k i k_i ki,问字符串 S S S 第 k i k_i ki 个字母是什么?
数据范围
1 ≤ ∣ S ∣ , q ≤ 2 ∗ 1 0 5 , 1 ≤ k i ≤ 1 0 18 1 \le |S|,q \le 2*10^5,1 \le k_i \le 10^{18} 1≤∣S∣,q≤2∗105,1≤ki≤1018
思路
令 n n n 为初始时 S S S 的长度。
不考虑大小写的话,第 k i k_i ki 个字母即为 S k i % n + 1 S_{k_i \% n +1} Ski%n+1。
现在要考虑第 k i k_i ki 个字母的大小写形式。
因为不考虑大小写的情况下,每次操作都是把 S S S 变成 S + S S+S S+S,所以第 i i i 次操作后, S S S 会翻倍 i i i 次, S S S 的长度为 2 i ∗ n 2^i*n 2i∗n。
令 f ( w , i d ) f(w,id) f(w,id) 为第 i d id id 个位置的字母的大小写,是否与初始时 S S S 对应位置的字母的大小写相同, 0 0 0 表示相同, 1 1 1 表示不同。
同时,第 w w w 次操作后,恰好包含了第 i d id id 个位置,换句话说, w w w 为满足 2 w ∗ n ≥ i d 2^w*n \ge id 2w∗n≥id 的最小值。
在 S S S 中前一半和后一半对应位置的大小写相反,具体的说,当 S S S 的长度为 2 w ∗ n 2^w*n 2w∗n 时,第 i i i 个位置 ( 1 ≤ i ≤ 2 w − 1 ∗ n ) (1 \le i \le 2^{w-1}*n) (1≤i≤2w−1∗n) 与 第 i + 2 w − 1 ∗ n i+2^{w-1}*n i+2w−1∗n 的位置的字母相同,大小写相反。
因此,若 i d ≤ 2 w − 1 ∗ n id \le 2^{w-1}*n id≤2w−1∗n,那么 f ( w , i d ) = f ( w − 1 , i d ) f(w,id) = f(w-1,id) f(w,id)=f(w−1,id),否则 f ( w , i d ) = f ( w − 1 , i d − 2 w − 1 ∗ n ) ⊕ 1 f(w,id) = f(w-1,id-2^{w-1}*n) \oplus 1 f(w,id)=f(w−1,id−2w−1∗n)⊕1。
特别的,当 w = 0 w=0 w=0 时,表示未操作时的初始串, f ( 0 , i d ) = 0 f(0,id)=0 f(0,id)=0。
因为上一个状态的长度都是当前状态长度的一半,所以求解 f ( w , i d ) f(w,id) f(w,id) 的复杂度为 O ( log 2 i d ) O(\log_2id) O(log2id)
复杂度
时间复杂度 O ( q ∗ log 2 k i ) O(q*\log_2 k_i) O(q∗log2ki),空间复杂度 O ( ∣ S ∣ ) O(|S|) O(∣S∣)
代码实现
// Problem: D - Strange Mirroring
// Contest: AtCoder - AtCoder Beginner Contest 380
// URL: https://atcoder.jp/contests/abc380/tasks/abc380_d
// Memory Limit: 1024 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;#define int long longconst int N = 1e6 + 5;int n, q;
string s;// 代码实现和思路有些不同,w传的是倍数,思路中传的是指数
int f(int w, int id)
{if (w == 1) {return 0;}int len = w * n;if (id <= len / 2) {return f(w / 2, id);} else {return f(w / 2, id - w / 2 * n) ^ 1;}
}void solve()
{cin >> s >> q;n = s.size();s = ' ' + s;while (q--) {int id;cin >> id;int p = (id - 1) % n + 1;char c = s[p];for (int i = 0; i <= 63; i++) {int w = 1ll << i;if (w * n >= id) {int op = f(w, id);if (op) {if (islower(c))c = toupper(c);elsec = tolower(c);}break;}}cout << c << ' ';}
}signed main()
{ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);int T = 1;// cin >> T;while (T--) {solve();}
}
E - 1D Bucket Tool
题意
有 n n n 个单元格,初始时第 i i i 个单元格的颜色为 i i i,第 i i i 个单元格与第 i + 1 i+1 i+1 个单元格相邻。
进行 q q q 次查询,查询有两种情况:
- 修改第 x x x 个单元格所在的同色连通块的颜色为 c c c。
- 输出颜色为 c c c 的单元格有多少个。
数据范围
1 ≤ n ≤ 5 ∗ 1 0 5 , 1 ≤ q ≤ 2 ∗ 1 0 5 1 \le n \le 5*10^5,1 \le q \le 2*10^5 1≤n≤5∗105,1≤q≤2∗105
思路
考虑用并查集维护同色连通块,并查集上需要维护连通块的单元格数,左边界和右边界。
对于操作 1 1 1,首先第 x x x 个单元格的颜色的单元格数会减少所在连通块的单元格数,然后把颜色 c c c 的单元格数增加所在连通块的单元格数。
如果修改颜色后,和左边连通块或者右边连通块颜色相同,则合并在一起。
对于操作 2 2 2,则直接输出记录的对应颜色单元格数即可。
复杂度
时间复杂度 O ( n + q ) O(n+q) O(n+q),空间复杂度 O ( n ) O(n) O(n)
代码实现
// Problem: E - 1D Bucket Tool
// Contest: AtCoder - AtCoder Beginner Contest 380
// URL: https://atcoder.jp/contests/abc380/tasks/abc380_e
// Memory Limit: 1024 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;#define int long longconst int N = 1e6 + 5;int n, q;
int p[N], lx[N], rx[N], sz[N], col[N], cnt[N];int find(int x)
{return x == p[x] ? x : p[x] = find(p[x]);
}void merge(int x, int y)
{x = find(x), y = find(y);if (x != y) {p[x] = y;lx[y] = min(lx[y], lx[x]);rx[y] = max(rx[y], rx[x]);sz[y] += sz[x];}
}void solve()
{cin >> n >> q;for (int i = 1; i <= n; i++) {cnt[i] = sz[i] = 1;p[i] = lx[i] = rx[i] = col[i] = i;}while (q--) {int op;cin >> op;if (op == 1) {int x, c;cin >> x >> c;x = find(x);cnt[col[x]] -= sz[x];col[x] = c;cnt[c] += sz[x];if (lx[x] != 1) {int fl = find(lx[x] - 1);if (col[fl] == c) {merge(x, fl);}}if (rx[x] != n) {int fr = find(rx[x] + 1);if (col[fr] == c) {merge(x, fr);}}} else {int c;cin >> c;cout << cnt[c] << '\n';}}
}signed main()
{ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);int T = 1;// cin >> T;while (T--) {solve();}
}
F - Exchange Game
题意
T a k a h a s h i Takahashi Takahashi 有 n n n 张卡片, A o k i Aoki Aoki 有 m m m 张卡片,初始时桌子上有 L L L 张卡片,每张卡片上都有数字。
T a k a h a s h i Takahashi Takahashi 和 A o k i Aoki Aoki 先后出牌, T a k a h a s h i Takahashi Takahashi 先手出牌,当前轮到某人出牌时,如果无牌可出则输,否则,可以出一张牌,如果当前桌子上有一张比刚出的牌更小的牌,则当前的出牌人可以拿起这张牌。
问哪个人必赢?
数据范围
n + m + L ≤ 12 n+m+L \le 12 n+m+L≤12,牌上的数字为正数,不超过 1 0 9 10^9 109
思路
注意到总牌数很少,对应的情况数必然不超过 3 n + m + L 3^{n+m+L} 3n+m+L,最大为 531 , 441 531,441 531,441,因此可以记忆化搜索所有的博弈状态,从而确定哪个人必赢。
其中可以加个小剪枝,就是如果要在出牌后,在桌子上拿牌的话,取小于刚出的牌的最大的牌是最优的,因为取得的牌越大,后面再打出就可能可以再次在桌上取牌,从而保持有牌的状态避免失败。
复杂度
时间复杂度 O ( 3 n + m + L ) O(3^{n+m+L}) O(3n+m+L),空间复杂度 O ( 3 n + m + L ) O(3^{n+m+L}) O(3n+m+L)
代码实现
// Problem: F - Exchange Game
// Contest: AtCoder - AtCoder Beginner Contest 380
// URL: https://atcoder.jp/contests/abc380/tasks/abc380_f
// Memory Limit: 1024 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;#define int long longconst int N = 1e6 + 5;int n, m, k;map<array<multiset<int>, 3>, int> f[2];int dfs(array<multiset<int>, 3> st, int op)
{if (f[op].count(st))return f[op][st];if (!st[op].size())return f[op][st] = 0;for (int x : st[op]) {auto it = st[2].lower_bound(x);int y = -1;if (st[2].size() && it != st[2].begin()) {y = *(--it);}array<multiset<int>, 3> ne = st;ne[op].erase(ne[op].lower_bound(x));if (y != -1) {ne[2].erase(ne[2].lower_bound(y));ne[op].insert(y);}ne[2].insert(x);if (!dfs(ne, op ^ 1))return f[op][st] = 1;}return f[op][st] = 0;
}void solve()
{cin >> n >> m >> k;array<multiset<int>, 3> st;for (int i = 0; i < n; i++) {int x;cin >> x;st[0].insert(x);}for (int i = 0; i < m; i++) {int x;cin >> x;st[1].insert(x);}for (int i = 0; i < k; i++) {int x;cin >> x;st[2].insert(x);}int flag = dfs(st, 0);cout << (flag ? "Takahashi" : "Aoki") << '\n';
}signed main()
{ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);int T = 1;// cin >> T;while (T--) {solve();}
}
相关文章:
)
AtCoder Beginner Contest 380(A-F)
比赛链接:AtCoder Beginner Contest 380(A-F) A - 123233 题意 给出一个数字 N N N,问这个数字中是否 1 1 1 恰好出现了 1 1 1 次, 2 2 2 恰好出现了 2 2 2 次, 3 3 3 恰好出现了 3 3 3 次。 数据范围 100000 ≤ N ≤ 99…...
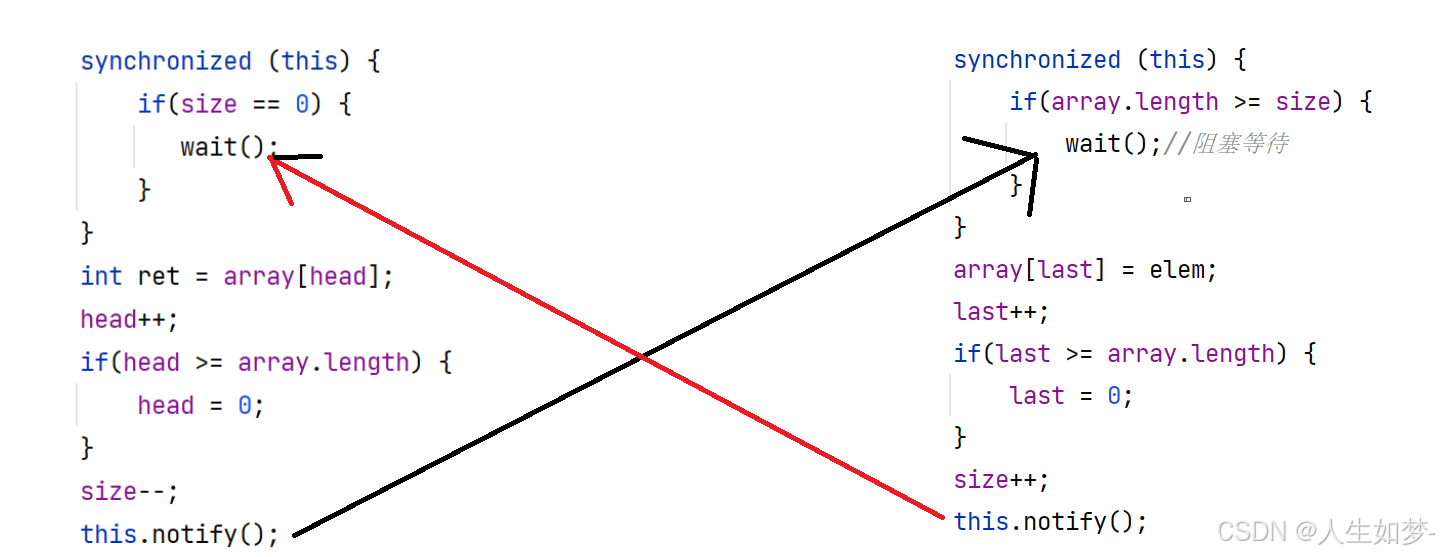
多线程-阻塞队列
目录 阻塞队列 消息队列 阻塞队列用于生产者消费者模型 概念 实现原理 生产者消费者主要优势 缺陷 阻塞队列的实现 1.写一个普通队列 2.加上线程安全和阻塞等待 3.解决代码中的问题 阻塞队列 阻塞队列,是带有线程安全功能的队列,拥有队列先进…...
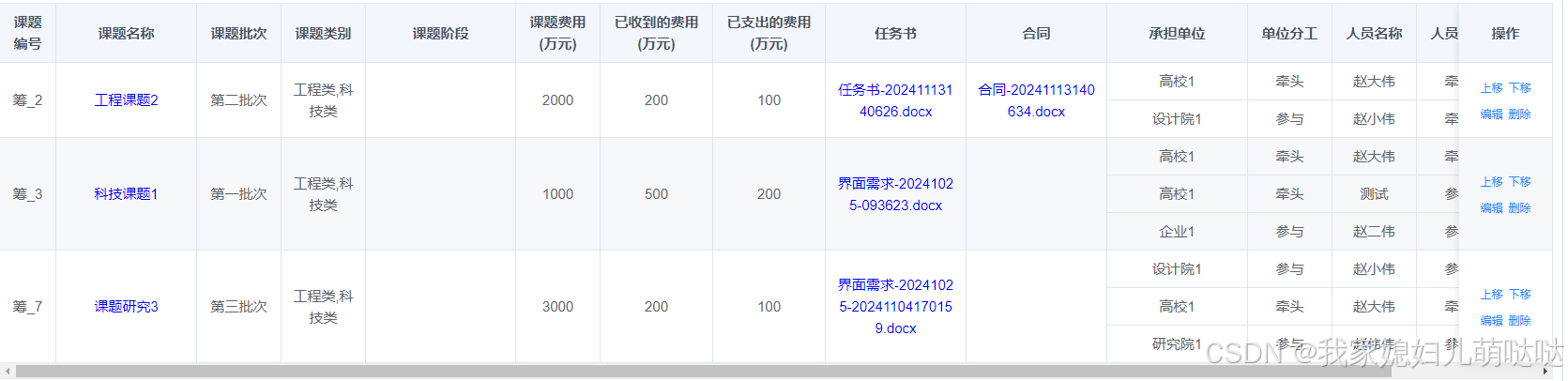
el-table合并单元格之后,再进行隔行换色的且覆盖表格行鼠标移入的背景色的实现
el-table 中有现成的隔行换色功能,只要增加 stripe 属性即可。但是如果有单元格合并的话,这个属性就不可用了。这时候我们就需要动点小心思了。 基于相同字段进行合并 单元格合并:基于表头中的某一列,具有相同值的个数相加进行合…...
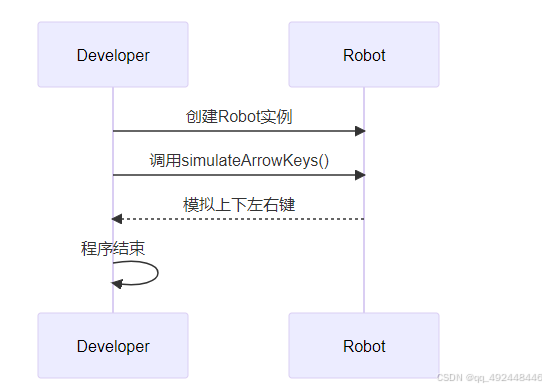
java模拟键盘实现selenium上下左右键 table中的左右滚动条实现滚动
在这篇文章中,我们将学习如何使用Java编程语言模拟键盘输入,特别是模拟上下左右方向键的操作。这是一个很有趣的项目,尤其适合刚入行的开发者。我们将分步进行,接下来,我们会通过表格展示整个实现过程,然后…...
SDF,一个从1978年运行至今的公共Unix Shell
关于SDF 最近发现了一个很古老的公共Unix Shell服务器,这个项目从1978年运行至今,如果对操作系统,对Unix感兴趣,可以进去玩一玩体验一下 SDF Public Access UNIX System - Free Shell Account and Shell Access 注册方式 我一…...

前馈神经网络 (Feedforward Neural Network, FNN)
代码功能 网络定义: 使用 torch.nn 构建了一个简单的前馈神经网络。 隐藏层使用 ReLU 激活函数,输出层使用 Sigmoid 函数(适用于二分类问题)。 数据生成: 使用经典的 XOR 问题作为数据集。 数据点为二维输入ÿ…...

【Python进阶】Python中的数据库交互:使用SQLite进行本地数据存储
1、数据持久化与访问效率 数据持久化是指程序运行过程中产生的数据能够长期保存,即使程序关闭或系统重启后仍可读取和修改。通过数据库,我们可以确保数据持久化的同时,实现数据的快速访问。例如,银行系统需要实时更新账户余额&am…...

ZooKeeper单机、集群模式搭建教程
单点配置 ZooKeeper在启动的时候,默认会读取/conf/zoo.cfg配置文件,该文件缺失会报错。因此,我们需要在将容器/conf/挂载出来,在制定的目录下,添加zoo.cfg文件。 zoo.cfg logback.xml 配置文件的信息可以从二进制包…...

函数指针示例
目录: 代码: main.c #include <stdio.h> #include <stdlib.h>int Max(int x, int y); int Min(int x, int y);int main(int argc, char**argv) {int x,y;scanf("%d",&x);scanf("%d",&y);int select;printf(&q…...

vue如何实现组件切换
一、使用条件渲染 (v-if) <template><div><button click"currentView ComponentA">Show Component A</button><button click"currentView ComponentB">Show Component B</button><component-a v-if"curren…...

计算机视觉 1-8章 (硕士)
文章目录 零、前言1.先行课程:python、深度学习、数字图像处理2.查文献3.环境安装 第一章:概论1.计算机视觉的概念2.机器学习 第二章:图像处理相关基础1.图像的概念2.图像处理3.滤波器4.卷积神经网络CNN5.图像的多层表示:图像金字…...

整数唯一分解定理
整数唯一分解定理,也称为算术基本定理,是由德国数学家高斯在其著作《算术研究》中首次提出的。本文回顾整数唯一分解定理以及对应的几个重要结论。 一、整数唯一分解定理 整数唯一分解定理,也称为算术基本定理,是数论中的一个重…...

Grass脚本2倍速多账号
前言,小编也是第一次撸空投,我是抱着试一试的态度,梦想总是要有的万一白嫖了呢 Grass 是什么? Grass 扩展程序是一款创新的工具,它可以帮助您释放未使用的网络资源的力量。 通过分享您的剩余带宽,您可以赚…...

15分钟学 Go 第 56 天:架构设计基本原则
第56天:架构设计基本原则 学习目标 理解和掌握基本的架构设计原则,以提升软件系统的可维护性、可扩展性和可重用性。 内容提纲 架构设计原则概述常见架构设计原则 单一职责原则 (SRP)开放/封闭原则 (OCP)里氏替换原则 (LSP)接口分离原则 (ISP)依赖反…...
)
HTML5 Video(视频)
HTML5 Video(视频) HTML5视频是现代网页设计中不可或缺的一部分,它允许开发者在网页中嵌入视频内容,为用户提供丰富多样的媒体体验。本文将深入探讨HTML5视频的各个方面,包括其基本用法、支持的格式、自定义播放器、浏览器兼容性以及最佳实践。 一、HTML5视频的基本用法 …...
)
开源模型应用落地-qwen模型小试-Qwen2.5-7B-Instruct-tool usage入门-串行调用多个tools(三)
一、前言 Qwen-Agent 是一个利用开源语言模型Qwen的工具使用、规划和记忆功能的框架。其模块化设计允许开发人员创建具有特定功能的定制代理,为各种应用程序提供了坚实的基础。同时,开发者可以利用 Qwen-Agent 的原子组件构建智能代理,以理解和响应用户查询。 本篇将介绍如何…...

MySQL:表设计
表的设计 从需求中获得类,类对应到数据库中的实体,实体在数据库中表现为一张一张的表,类中的属性就对应着表中的字段(也就是表中的列) 表设计的三大范式: 在数据库设计中,三大范式࿰…...

173. 二叉搜索树迭代器【 力扣(LeetCode) 】
文章目录 零、原题链接一、题目描述二、测试用例三、解题思路四、参考代码 零、原题链接 173. 二叉搜索树迭代器 一、题目描述 实现一个二叉搜索树迭代器类BSTIterator ,表示一个按中序遍历二叉搜索树(BST)的迭代器: BSTIterato…...
)
大三学生实习面试经历(1)
最近听了一位学长的建议,不能等一切都准备好再去开始,于是就开始了简历投递,恰好简历过了某小厂的初筛,开启了线上面试,记录了一些问题: (通过面试也确实了解到了自己在某些方面确实做的还不够…...

【论文复现】STM32设计的物联网智能鱼缸
📝个人主页🌹:Eternity._ 🌹🌹期待您的关注 🌹🌹 ❀STM32设计的物联网智能鱼缸 【1】项目功能介绍【2】设计需求总结【3】项目硬件模块组成 1.2 设计思路【1】整体设计思路【2】ESP8266工作模式…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...
