LeetCode-215.数组中的第K个最大元素
. - 力扣(LeetCode)给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1:
输入: [3,2,1,5,6,4], k = 2
输出: 5
示例 2:
输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4
提示:
1 <= k <= nums.length <= 105-104 <= nums[i] <= 104
思路1:基于堆排序的选择方法
排序 - - - 选择排序(简单选择、堆排序)_c#排序中选择排序中的dui排序-CSDN博客
「调整」
父节点都大于或小于子结点
// 以root为根,调整大根堆void heapAdjust(vector<int>& nums, int root, int heapSize){int i = root; // i保存根节点下标for(int j = i*2 + 1; j < heapSize; j = i*2+1){// j保存孩子中最大值下标if(j < heapSize - 1 && nums[j] < nums[j+1]){j++;}if(nums[i] >= nums[j]){break;}else{swap(nums[i], nums[j]);i = j;}}}「建堆」
将排序码k1,k2,k3,…,kn表示成一棵完全二叉树,然后从第 n/2个排序码(即树的最后一个非终端结点)开始筛选,使由该结点作根结点组成的子二叉树符合堆的定义,然后从第 n/2-1 个排序码重复刚才操作,直到第一个排序码止。
void buildHeap(vector<int>&nums, int heapSize){for(int i = heapSize / 2; i >= 0; i--){heapAdjust(nums, i, heapSize);}}「删除」
将堆中第一个结点(二叉树根结点)和最后一个结点的数据进行交换(k1与kn),再将k1~kn-1重新建堆,然后k1和kn-1交换,再将k1~kn-2重新建堆,然后k1和kn-2交换,如此重复下去,每次重新建堆的元素个数不断减1,直到重新建堆的元素个数仅剩一个为止。这时堆排序已经完成,则排序码k1,k2,k3,…,kn已排成一个有序序列。
class Solution {
private:// 以root为根,调整大根堆void heapAdjust(vector<int>& nums, int root, int heapSize){int i = root; // i保存根节点下标for(int j = i*2 + 1; j < heapSize; j = i*2+1){// j保存孩子中最大值下标if(j < heapSize - 1 && nums[j] < nums[j+1]){j++;}if(nums[i] >= nums[j]){break; // 因为从叶子节点向上调节,所以没有节点交换,其子树也不许变化}else{swap(nums[i], nums[j]);i = j; // j节点调整,其子树也需要调整}}}void buildHeap(vector<int>&nums, int heapSize){for(int i = heapSize / 2; i >= 0; i--){heapAdjust(nums, i, heapSize);}}public:int findKthLargest(vector<int>& nums, int k) {int heapSize = nums.size();buildHeap(nums, heapSize);// 第k大数倒数for(int i = nums.size() - 1; i > nums.size() - k; --i){swap(nums[0],nums[i]);--heapSize;heapAdjust(nums, 0, heapSize);}return nums[0];}
};思路2:基于快速排序的选择方法
排序 - - - 交换排序(快速排序、冒泡排序)-CSDN博客
class Solution {
private:int partition(vector<int>&nums, int l, int r){int key = nums[l];while(l < r){while(l < r && nums[r] >= key) r--;nums[l] = nums[r];while(l < r && nums[l] <= key) l++;nums[r] = nums[l];}nums[l] = key;return l;}int quickSelect(vector<int>& nums, int l, int r, int k){int index = partition(nums, l, r);if(index == k)return nums[k];elsereturn index < k ? quickSelect(nums, index + 1, r, k) // index数小于第k数则在index右边查找: quickSelect(nums, l, index - 1, k); // index数大于第k数则在index左边查找}public:int findKthLargest(vector<int>& nums, int k) {return quickSelect(nums, 0, nums.size() - 1, nums.size() - k); // 返回倒数k位置数}
};相关文章:

LeetCode-215.数组中的第K个最大元素
. - 力扣(LeetCode)给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。 请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。 你必须设计并实现时间复杂度为 O(n) 的算法解决此问…...

『OpenCV-Python』视频的读取和保存
点赞 + 关注 + 收藏 = 学会了 推荐关注 《OpenCV-Python专栏》 上一讲介绍了 OpenCV 的读取图片的方法,这一讲简单聊聊 OpenCV 读取和保存视频。 视频的来源主要有2种,一种是本地视频文件,另一种是实时视频流,比如手机和电脑的摄像头。 要读取这两种视频的方法都是一样的…...

什么是Spring Boot Actuator
Spring Boot Actuator是一个用于监控和管理Spring Boot应用的框架,它提供了生产级别的功能,如健康检查、审计、指标收集、HTTP跟踪等。以下是对Spring Boot Actuator的详细介绍: 一、主要功能和特点 监控和管理: 提供多种内置端点…...

计算机网络:运输层 —— 运输层端口号
文章目录 运输层端口号的分类端口号与应用程序的关联应用举例发送方的复用和接收方的分用 运输层端口号的分类 端口号只具有本地意义,即端口号只是为了标识本计算机网络协议栈应用层中的各应用进程。在因特网中不同计算机中的相同端口号是没有关系的,即…...

linux下编译安装memcached
一、安装依赖库 Memcached依赖于一些系统库,在大多数Linux发行版中,需要安装libevent库。 Debian/Ubuntu系统 使用以下命令安装依赖库: sudo apt -y update sudo apt -y install libevent - devCentOS/RHEL系统 可以通过以下命令安装&am…...

最短路径生成树的数量-黑暗城堡
信息学奥赛一本通T1486-黑暗城堡 时间限制: 2s 内存限制: 192MB 提交: 18 解决: 9 题目描述 知道黑暗城堡有 N 个房间,M 条可以制造的双向通道,以及每条通道的长度。 城堡是树形的并且满足下面的条件: 设 Di为如果所有的通道都被修建…...

将已有的MySQL8.0单机架构变成主从复制架构
过程: 把数据库做一个完全备份, 恢复到从节点上, 恢复后从备份的那个点开始往后复制,从而保证后续数据的一致性。 步骤: 修改 master 主节点 的配置( server-id log-bin )master 主节点 完全备份( mysqldump )master 主节点 创建…...

JSON.stringify的应用说明
前言 JSON.stringify() 方法将 JavaScript 对象转换为字符串,在日常开发中较常用,但JSON.stringify其实有三个参数,后两个参数,使用较少,今天来介绍一下后两个参数的使用场景和示例。 语法及参数说明 JSON.stringify()…...
)
pyflink datastream数据流ds经过一系列转换后转为table,t_env.from_data_stream(ds)
在 pyflink 处理数据流过程中,有时候需要将data_stream转为table,下面是正确的方式,即每一个算子(map,reduce, window)操作之后需要指定输出数据类型。 from pyflink.common.typeinfo import Types from pyflink.datastream import StreamEx…...

vxe-grid table 校验指定行单元格的字段,只校验某个列的字段
Vxe UI vue vxe-table 中校验表格行是非常简单的,只需要配置好校验规则,然后调用 validate 方法就可以自动完成校验,但是由于项目淡色特殊需求,在某个单元格的值修改后需要对另一个列的值就行校验,这个时候又不需要全部…...
)
【Java多线程】单例模式(饿汉模式和懒汉模式)
目录 单例模式的定义: 饿汉式--单例模式 定义: 案例: 优缺点: 懒汉式--单例模式: 定义: 1)懒汉式单例模式(非线程安全) 2)线程安全的懒汉式单例模…...

python 异步编程之协程
最近在学习python的异步编程,这里就简单记录一下,免得日后忘记。 首先,python异步实现大概有三种方式,多进程,多线程和协程;多线程和多进程就不用多说了,基本上每种语言都会有多进行和多线程的…...

现代密码学|古典密码学例题讲解|AES数学基础(GF(2^8)有限域上的运算问题)| AES加密算法
文章目录 古典密码凯撒密码和移位变换仿射变换例题多表代换例题 AES数学基础(GF(2^8)有限域上的运算问题)多项式表示法 | 加法 | 乘法X乘法模x的四次方1的乘法 AES加密算法初始变换字节代换行移位列混合轮密钥加子密钥(…...

算法沉淀一:双指针
目录 前言: 双指针介绍 对撞指针 快慢指针 题目练习 1.移动零 2.复写零 3.快乐数 4.盛水最多的容器 5.有效三角形的个数 6.和为s的两个数 7.三数之和 8.四数之和 前言: 此章节介绍一些算法,主要从leetcode上的题来讲解ÿ…...
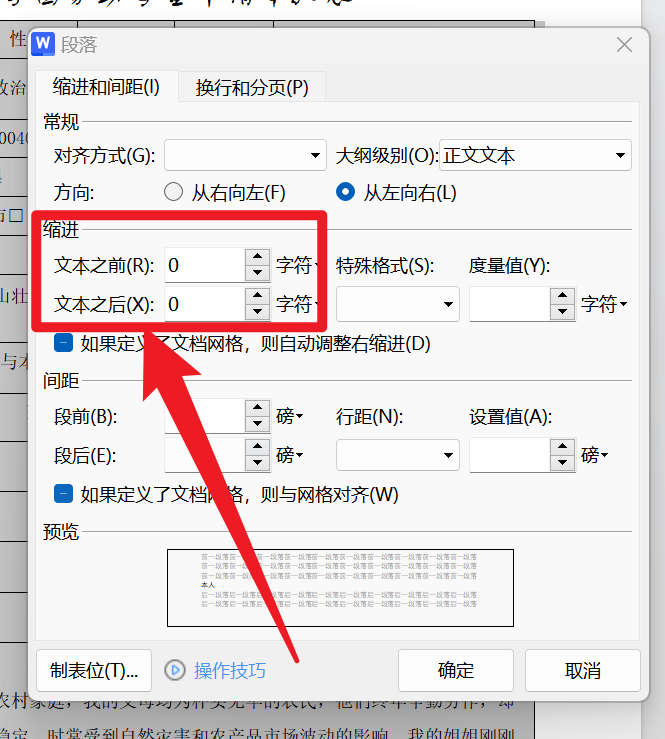
Word_小问题解决_1
1.第二页是空白的,但是删不掉 将鼠标弄到第二页最开始的地方打开段落设置行距为固定值0.7磅 2.表格中有文字进入了表格中怎么办 打开段落,将缩进改为0即可...

基于opencv制作GUI界面
可以基于cvui头文件实现一些控件操作,头文件及demo实例 这是一个demo main.cpp #include <opencv2/opencv.hpp> #define CVUI_IMPLEMENTATION #include "cvui.h"#define WINDOW_NAME "CVUI Hello World!"int main(void) {cv::Mat frame…...

微服务即时通讯系统的实现(客户端)----(2)
目录 1. 将protobuf引入项目当中2. 前后端交互接口定义2.1 核心PB类2.2 HTTP接口定义2.3 websocket接口定义 3. 核心数据结构和PB之间的转换4. 设计数据中心DataCenter类5. 网络通信5.1 定义NetClient类5.2 引入HTTP5.3 引入websocket 6. 小结7. 搭建测试服务器7.1 创建项目7.2…...

QT使用libssh2库实现sftp文件传输
本篇文章通过用户名和密码来连接服务器端,通过密匙连接服务器端可以参考另外一篇文章: https://blog.csdn.net/u012372584/article/details/143826199?sharetype=blogdetail&sharerId=143826199&sharerefer=PC&sharesource=u012372584&spm=1011.2480.3001.…...

【Linux】进程的优先级
进程的优先级 一.概念二.修改优先级的方法三.进程切换的大致原理:四.上下文数据的保存位置: 一.概念 cpu资源分配的先后顺序,就是指进程的优先权(priority)。 优先权高的进程有优先执行权利。配置进程优先权对多任务环…...

python实现十进制转换二进制,tkinter界面
目录 需求 效果 代码实现 代码解释 需求 python实现十进制转换二进制 效果 代码实现 import tkinter as tk from tkinter import messageboxdef convert_to_binary():try:# 获取输入框中的十进制数decimal_number int(entry.get())# 转换为二进制binary_number bin(de…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...
