WPF如何全局应用黑白主题效果
灰白色很多时候用于纪念,哀悼等。那么使用 WPF如何来做到这种效果呢?要实现的这种效果,我们会发现,它其实不仅仅是要针对图片,而是要针对整个窗口来实现灰白色。
如果只是针对图片的话,我可以可以对图片进行灰阶转换,即可达到灰色效果。
以下是图片转灰阶的代码,当然方法不仅仅是这一种:
//……省略……FormatConvertedBitmap grayImage = new FormatConvertedBitmap();grayImage.BeginInit();grayImage.Source = originImage as BitmapSource;grayImage.DestinationFormat = PixelFormats.Gray32Float;grayImage.EndInit();//……省略……
上述方法也可以直接在 xaml里面表示。
<Image.Source><FormatConvertedBitmap DestinationFormat="Gray32"><FormatConvertedBitmap.Source><BitmapImage UriSource="Images\1.png" /></FormatConvertedBitmap.Source></FormatConvertedBitmap></Image.Source>
如果我们想针对整个窗口应用这种灰色的效果,那我们可以用着色器特效( ShaderEffect)来实现。
说明:
-
*.fx格式文件:是一种应用特效效果文件,也叫渲染管线的配置文件。编写该文件语言名为高阶着色器语言(High Level Shader Language,简称HLSL),由微软拥有及开发的一种语言。 -
*.ps格式文件:是通过*.fx文件编译出来的文件,该文件是通过ShaderEffect所指定的原始文件。通过ShaderEffect类,将其应用于WPF。
灰阶相关 fx, ps等文件已有大佬写好了,我们直接拿来用即可跳转下载(https://github.com/abursjoo/GrayscaleEffectSample/tree/master/WpfApplication1/WpfApplication1)。相关解释,会在注释中说明。
渲染管线配置文件(*.fx)
//sampler2D 2D纹理采样器//s0中,s表示取样器,0是表示取样器的子组件编号sampler2D implicitInput : register(s0);//c 表示缓冲区偏移量float factor : register(c0);//TEXCOORD 表示纹理坐标;COLOR 漫反射/镜面反射颜色float4 main(float2 uv : TEXCOORD) : COLOR{//返回纹理implicitInput在uv位置的颜色。float4 color = tex2D(implicitInput, uv);//将颜色转成灰阶float gray = color.r * 0.3 + color.g * 0.59 + color.b *0.11;float4 result;result.r = (color.r - gray) * factor + gray;result.g = (color.g - gray) * factor + gray;result.b = (color.b - gray) * factor + gray;result.a = color.a;return result;}
应用WPF中特效类
//灰阶特效public class GrayscaleEffect : ShaderEffect{//将像素着色器映射到灰阶着色器private static PixelShader _pixelShader = new PixelShader() { UriSource = new Uri(@"pack://application:,,,/GrayscaleEffect;component/GrayscaleEffect.ps") };public GrayscaleEffect(){PixelShader = _pixelShader;//更新着色器的值UpdateShaderValue(InputProperty);//该属性可以不要,该熟悉用于彩色到灰色过渡效果UpdateShaderValue(DesaturationFactorProperty);}public static readonly DependencyProperty InputProperty = ShaderEffect.RegisterPixelShaderSamplerProperty("Input", typeof(GrayscaleEffect), 0);public Brush Input{get { return (Brush)GetValue(InputProperty); }set { SetValue(InputProperty, value); }}public static readonly DependencyProperty DesaturationFactorProperty = DependencyProperty.Register("DesaturationFactor", typeof(double), typeof(GrayscaleEffect), new UIPropertyMetadata(0.0, PixelShaderConstantCallback(0), CoerceDesaturationFactor));//用于调节过渡效果public double DesaturationFactor{get { return (double)GetValue(DesaturationFactorProperty); }set { SetValue(DesaturationFactorProperty, value); }}private static object CoerceDesaturationFactor(DependencyObject d, object value){GrayscaleEffect effect = (GrayscaleEffect)d;double newFactor = (double)value;if (newFactor < 0.0 || newFactor > 1.0){return effect.DesaturationFactor;}return newFactor;}}在 WPF里面的使用示例:
<!--effect 代表GrayscaleEffect所在的命名空间--><Grid.Effect><effect:GrayscaleEffect/></Grid.Effect>需要应用到哪个根元素上,就将该特效给对应元素的 Effect 赋值即可。
这种实现方法,性能还是很不错的,如果想对 Shader有更深入的认识,可以阅读 《DirectX3DHLSL高级实例精讲》.
相关文章:

WPF如何全局应用黑白主题效果
灰白色很多时候用于纪念,哀悼等。那么使用 WPF如何来做到这种效果呢?要实现的这种效果,我们会发现,它其实不仅仅是要针对图片,而是要针对整个窗口来实现灰白色。 如果只是针对图片的话,我可以可以对图片进…...

[Qt] Qt删除文本文件中的某一行
需求 我们经常读一个文件或者直接往一个空白文件中写文本,那么该如何使用Qt在一个文本文件中删除某一行 代码 #include <QCoreApplication> #include <QIODevice> #include <QFile> #include <QTextStream> #include <QString> #i…...

【HarmonyOS学习日志(9)】一次开发,多端部署之界面级一多开发
关于一次开发,多端部署 一次开发多端部署就是指一套代码工程,一次开发上架,多端按需部署(一多),用于支撑开发者快速高效地开发多终端设备上的应用,以节省开发成本。 HarmonyOS系统面向多终端&…...

基于Java+SSM+JSP+MYSQL实现的宠物领养收养管理系统功能设计与实现六
一、前言介绍: 免费学习:猿来入此 1.1 项目摘要 随着人们生活水平的提高,宠物已经成为越来越多家庭的重要成员。然而,宠物的数量增长也带来了一系列问题,如流浪宠物数量的增加、宠物健康管理的缺失以及宠物领养收养…...

Java项目实战II基于微信小程序的课堂助手(开发文档+数据库+源码)
目录 一、前言 二、技术介绍 三、系统实现 四、文档参考 五、核心代码 六、源码获取 全栈码农以及毕业设计实战开发,CSDN平台Java领域新星创作者,专注于大学生项目实战开发、讲解和毕业答疑辅导。获取源码联系方式请查看文末 一、前言 在数字化教…...

解析 Android WebChromeClient:提升 WebView 用户体验的关键组件
文章目录 一、总览二、详细说明三、一些实际和有趣的应用四、最佳实践五、与其他组件的比较六、安全性考虑:防止 XSS 攻击与数据泄露6.1 介绍6.2 代码案例6.2.1 输入过滤6.2.2 Content Security Policy (CSP) 案例 六、总结 在 Android 开发中,WebChrome…...

【LeetCode热题100】字符串
本篇博客记录了关于字符串相关的几道题目,包括最长公共前缀、最长回文子串、二进制求和、字符串相乘。 //解法1 class Solution { public:string longestCommonPrefix(vector<string>& strs) {string ret strs[0];for(int i 1 ; i < strs.size() ; i…...
OceanBase 闪回查询
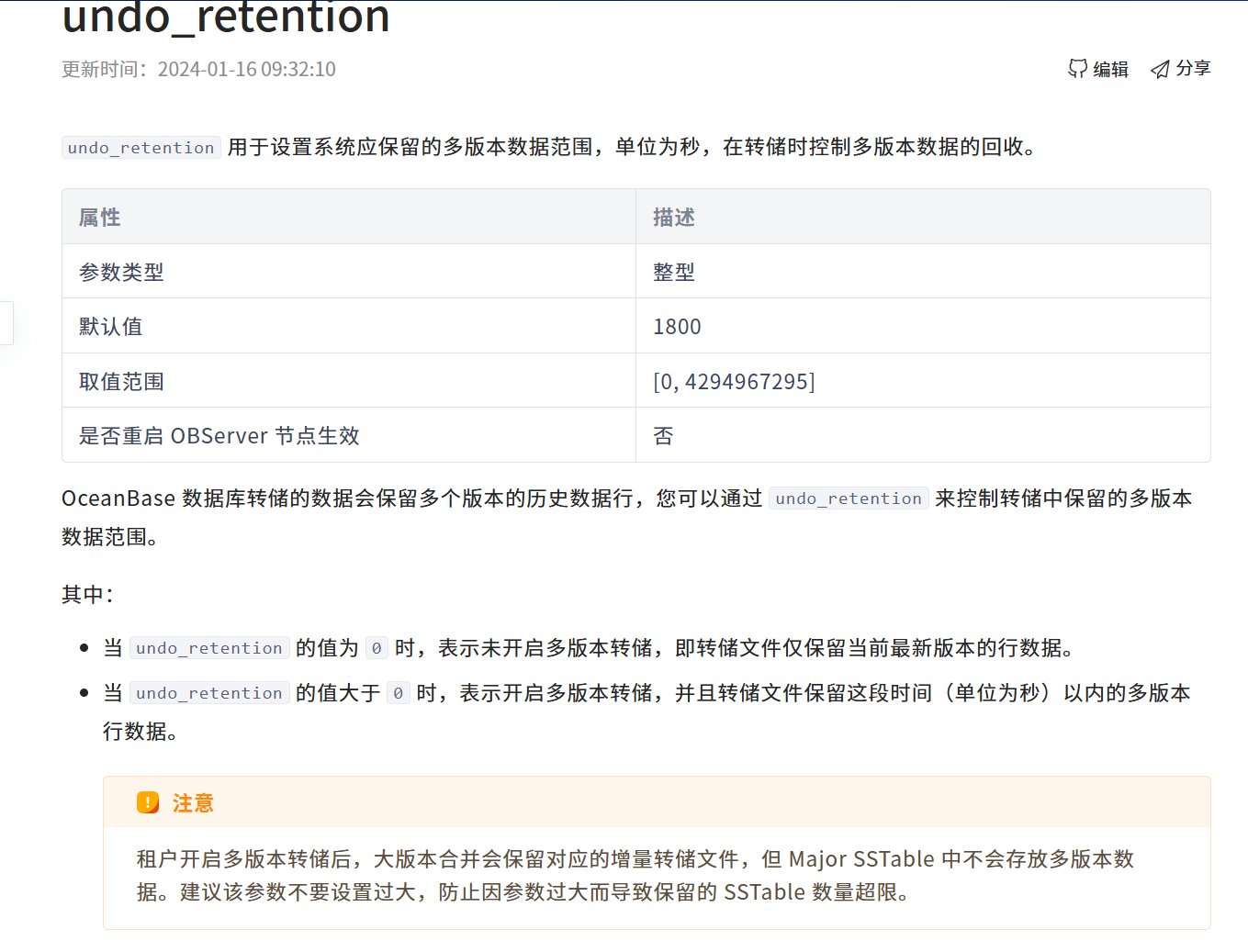
前言 在OB中,drop表可以通过 回收站 或者 以往的备份恢复来还原单表。当delete数据时,由于delete操作的对象不会进入回收站,此时需要通过闪回查询功能查看delete的数据,以便后续恢复 本次实验版本为 OceanBase 4.2.1.8࿰…...

C++析构函数详解
C析构函数详解:对象销毁与资源清理 在 C 中,析构函数是与构造函数相对应的特殊成员函数,它在对象生命周期结束时被自动调用,用于执行对象销毁之前的清理操作。析构函数主要用于释放对象占用的资源,如动态分配的内存、打…...

【网络安全 | 漏洞挖掘】未授权获取AI聊天内容
未经许可,不得转载。 文章目录 两天前,我收到了一项私人项目的邀请,内容看起来像是一个聊天机器人,类似于 Gemini 或 ChatGPT。于是我开始测试该项目的一些业务逻辑漏洞和 IDOR(不当访问控制)漏洞。尽管这个产品拥有一个强大的安全团队,网站上也部署了 WAF(Web 应用防火…...
)
时间序列分析——移动平均法、指数平滑法、逐步回归法、趋势外推法等(基于Python实现)
第 11章——时间序列分析和预测 【例11-1】 绘制时间序列折线图—观察成分 【代码框11-1】——绘制时间序列折线图 # 图11-2的绘制代码 import pandas as pd import matplotlib.pyplot as plt plt.rcParams[font.sans-serif]=[SimHei...

opencv(c++)----图像的读取以及显示
opencv(c)----图像的读取以及显示 imread: 作用:读取图像文件并将其加载到 Mat 对象中。参数: 第一个参数是文件路径,可以是相对路径或绝对路径。第二个参数是读取标志,比如 IMREAD_COLOR 表示以彩色模式读取图像。 返回值&#x…...
【PyTorch系统学习】)
PyTorch——从入门到精通:PyTorch基础知识(张量)【PyTorch系统学习】
什么是张量(Tensor) 张量在数学中是一个代数对象,描述了与矢量空间相关的代数对象集之间的多重线性映射。张量是向量和矩阵概念的推广,可以理解为多维数组。作为数学中的一个基本概念,张量有着多种类型,…...
ubuntu20安装jdk7,多版本管理)
(笔记)ubuntu20安装jdk7,多版本管理
前往 Oracle JDK 7 下载页面(需要 Oracle 账户),下载 JDK 7 的压缩包文件(.tar.gz)。 下载完成后,将文件解压到 /opt 目录: sudo tar -xzf jdk-7u<version>-linux-x64.tar.gz -C /opt 重…...

Python系列教程
文章目录 1. Python基础2. Python基础库3. Python数据分析 1. Python基础 语句数据类型表达式输入、输出与文件读写函数模块与包类与面向对象作用域与命名空间常用技巧与操作 2. Python基础库 Typing库 3. Python数据分析...

如何恢復電腦IP地址的手動設置?
手動設置IP地址後,可能會遇到一些網路連接問題,或者需要恢復到之前的自動獲取狀態。這篇文章將詳細介紹如何恢復電腦的IP地址設置。 為什麼需要恢復IP地址設置? 網路連接問題:手動設置IP地址後,可能會導致與路由器或…...

Linux 下敏感文件路径总结
Linux 下敏感文件路径总结 在服务器运维和安全测试过程中,掌握各类服务的关键配置文件路径、日志文件位置以及重要目录的存放位置至关重要。本文整理了 Linux 系统下常见服务(如 Apache、Nginx、MySQL 等)的路径结构,以及一些敏感…...

gitlab 服务器集群配置及 存储扩展配置
配置 GitLab 服务器集群并实现存储扩展是一个复杂的任务,但可以通过以下步骤来实现。GitLab 本身支持高可用性和分布式部署,可以显著提高系统的可靠性和性能。 ### 1. 规划和准备 #### 1.1 确定服务器数量 - **1 台负载均衡器**:用于分发请…...

3D Gaussian Splatting 代码层理解之Part2
现在让我们来谈谈高斯分布。我们已经在Part1介绍了如何根据相机的位置获取 3D 点并将其转换为 2D。在本文中,我们将继续处理高斯泼溅的高斯部分。这里用到的是代码库 GitHub 中part2. 我们在这里要做的一个小改动是,我们将使用透视投影,它利用与上一篇文章中所示的不同内部…...
有什么区别?什么情况下使用哪个?)
.length和.length()有什么区别?什么情况下使用哪个?
在编写程序的时候,我们经常发现有时候需要得到长度的时候我们使用函数.length,而有的时候用的却是.length()。 在对Java一知半解的时候,我曾产生了深深的疑惑,到底这两个有什么区别,为什么有时候要有括号,而…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...
