半导体器件与物理篇3 P-N结
热平衡时的PN结
pn结的定义:由p型半导体和n型半导体接触形成的结
pn结的特性和关键变量包括:整流性(即电流单向导通的特性)、平衡费米能级(费米能级 E F E_F EF为常数, d E F d x = 0 )、内建电势 \frac{dE_F}{dx}=0)、内建电势 dxdEF=0)、内建电势V_{bi}、空间电荷区(亦称为耗尽层)
我们将从这些性质入手,由浅入深、从定性到定量的角度去探讨pn结
PN结特性1:整流性
pn结的整流性,即只允许电流单向导通
pn结特性2:费米能级 E F E_F EF为常数,即 d E F d x = 0 \frac{dE_F}{dx}=0 dxdEF=0
产生原因:在热平衡时,也就是在给定温度之下,没有任何外界扰动,流经pn结的电子电流和空穴电流都为零。因此,对于每一种载流子,电场造成的漂移电流必须与浓度梯度引起的扩散电流完全抵消
关键公式: d E F d x = 0 \frac{dE_F}{dx}=0 dxdEF=0
由公式可以得到:在热平衡时,PN结内部的费米能级相同
(PS:能带图在保证各自的费米能级相同时,导带底部和价带顶部会进行一个渐变的变化)
pn结特性3:内建电势 V b i V_{bi} Vbi
内建电势 V b i V_{bi} Vbi的推导思路
我们现在理一下思路。假如现在有两块半导体a和b,全部都是本征半导体。
a和b拼在一起则电势差为零,也没有了内建电势。
那什么时候有电势差呢?
我对半导体a掺入了受主杂质,使其空穴浓度迅猛增加;此时我即使不对b进行操作,a中的电势也会下降。为什么电视会下降呢?
因为a中的空穴太多,就会扩散到b中。
本来a和b都是平衡的,但这个时候b那一侧因为扩散而有了更多的空穴,于是带了正电。
这个时候如果我再把正电荷从半导体a搬运到半导体b,则需要克服这部分正电荷产生的电场力。
电势差这不就产生了吗。
同样我们页可以知道,当半导体a掺入越多的受主杂质,除了电离产生的空穴越来越多,其费米能级 E F E_F EF也会越接近价带,并越偏离本征费米能级 E i E_i Ei。
此可以通过半导体a的 ( E i − E F ) (E_i-E_F) (Ei−EF)间接算出半导体a这一侧的电势 ψ p \psi_p ψp。
往a中掺入受主杂质还不够,我还往半导体b中掺入施主杂质,使b中充满了电离产生的自由电子。
那么,同理也会使半导体b的电势 ψ n \psi_n ψn上升。
用同样的方法算出b侧的电势,两者相减不就得到了两块半导体之间的内间电势(差)了吗?
其他科学家已经帮我们把 ( E i − E F ) (E_i-E_F) (Ei−EF)和 ψ n 和 ψ p \psi_n和\psi_p ψn和ψp的关系式求好了,我们拿来用就行: ψ p = − q q ( E i − E F ) \psi_p=-\frac{q}{q}(E_i-E_F) ψp=−qq(Ei−EF)
心动不如行动,我们这就立刻开始进行求解。
内建电势 V b i V_{bi} Vbi的推导过程
1.我们先列出包含 ( E i − E F ) (E_i-E_F) (Ei−EF)的表达式,恰巧我知道一个,就是p区和n区各自多子的浓度表达式: p 区多子浓度 p = n i e x p ( E i − E F k T p区多子浓度p=n_iexp(\frac{E_i-E_F}{kT} p区多子浓度p=niexp(kTEi−EF
p区和n区的少子浓度,我们先假设为0
对p区的多子浓度表达式进行换算,得到: E i − E F = k T l n p n i E_i-E_F=kTln\frac{p}{n_i} Ei−EF=kTlnnip
我们来分析一下上面这个式子中。
kT是温度,室温下为300K(以开);本征载流子浓度 n i = 9.65 × 1 0 9 c m − 3 n_i=9.65\times 10^{9} cm^{-3} ni=9.65×109cm−3
你问我 n i n_i ni怎么来的?我带你回顾一下《半导体器件与物理篇1 热平衡时能带和载流子浓度》中的表格吧:
同时一些室温下(300K)重要的常数需要牢记:
| 普朗克常量 h = 6.63 ⋅ 1 0 − 34 J ⋅ s h=6.63\cdot 10^{-34} J\cdot s h=6.63⋅10−34J⋅s | - |
|---|---|
| Si | N c = 2.86 × 1 0 19 c m − 3 N_c=2.86\times 10^{19} cm^{-3} Nc=2.86×1019cm−3 |
| - | N v = 2.66 × 1 0 19 c m − 3 N_v=2.66\times 10^{19} cm^{-3} Nv=2.66×1019cm−3 |
| - | n i = 9.65 × 1 0 9 c m − 3 n_i=9.65\times 10^{9} cm^{-3} ni=9.65×109cm−3 |
| GaAs | N c = 4.7 × 1 0 17 c m − 3 N_c=4.7\times 10^{17} cm^{-3} Nc=4.7×1017cm−3 |
| - | N v = 7.0 × 1 0 18 c m − 3 N_v=7.0\times 10^{18} cm^{-3} Nv=7.0×1018cm−3 |
| - | n i = 2.25 × 1 0 6 c m − 3 n_i=2.25\times 10^{6} cm^{-3} ni=2.25×106cm−3 |
那有哪些变量是未知的呢?
载流子浓度 p p p呀!!!
所以第二步,我们就要把这不好直接看出来的这个载流子浓度 p p p,转变成我们可以看出来的变量。
比如说,我们对这块半导体掺入了多少杂质( N A 和 N D N_A和N_D NA和ND)
2.于是,让我们翻找一下,有哪个公式既包含了载流子浓度,有包含了 N A 和 N D N_A和N_D NA和ND呢?
已知泊松方程式: d 2 ψ d x 2 = d E d x = ρ s ε s = q ( p − n + N D + − N A − ε s \frac{d^2\psi}{dx^2}=\frac{dE}{dx}=\frac{\rho_s}{\varepsilon_s}=\frac{q(p-n+N_D^{+}-N_A^{-}}{\varepsilon_s} dx2d2ψ=dxdE=εsρs=εsq(p−n+ND+−NA−
由空间电荷密度 ρ s \rho_s ρs的表达式可以知道,载流子的浓度需要与其对应的提供者——施主和受主杂质浓度相减。因此在正常情况下,在空间电荷密度应该为0
由此可得整个泊松方程式都为0: p − n + N D + − N A − = 0 p-n+N_D^{+}-N_A^{-}=0 p−n+ND+−NA−=0
这样一来,我们就凑齐了计算电势 ψ p \psi_p ψp最后的一块拼图: { p = N A − n = N D + \begin{cases} p=N_A^{-}\\n=N_D^{+}\end{cases} {p=NA−n=ND+
掺杂浓度 N A 和 N D N_A和N_D NA和ND右上角的正负号,表示的是电离的杂质。
最后,我们把所有的龙珠集合起来,就得到了: ψ p = − k T q l n N A n i \psi_p=-\frac{kT}{q}ln\frac{N_A}{n_i} ψp=−qkTlnniNA
3.同理,我们可以得到n区的电势: ψ n = − k T q l n N D n i \psi_n=-\frac{kT}{q}ln\frac{N_D}{n_i} ψn=−qkTlnniND
4.将n区和p区的电势相减,就得到了两区之间的电势差,也就是内建电势 V b i V_{bi} Vbi: V b i = ψ n − ψ p = k T q l n N A N D n i 2 V_{bi}=\psi_n-\psi_p=\frac{kT}{q}ln\frac{N_AN_D}{n_i^2} Vbi=ψn−ψp=qkTlnni2NAND
Pn结特性4:空间电荷区
空间电荷区,也称耗尽层abrupt junction,是指在pn结中,由于自由电子的扩散运动和内电场导致的漂移运动,使得p区和n区的交界处产生的一个薄电荷层
耗尽层其实有两部分,分别是过渡区和可动载流子浓度为0的完全耗尽区。一般将过渡区忽略。
由于“可动载流子浓度为0”,可以得到 p = n = 0 p=n=0 p=n=0
将 p = n = 0 p=n=0 p=n=0代入泊松方程式,得到: d 2 ψ d x 2 = q ε s ( N A − N D ) \frac{d^2\psi}{dx^2}=\frac{q}{\varepsilon_s}(N_A-N_D) dx2d2ψ=εsq(NA−ND)
耗尽区abrupt junction有两种,分别是突变结和线性缓变结。突变结也分为一般的(通用的)突变结和单边突变结
突变结
突变结是浅扩散或低能离子注入形成的pn结。
因此,当题目提及浅扩散或低能离子注入时,则代入突变结的知识点进行计算
假设掺杂的时候都把半导体给掺均匀了。
我们需要求解这一块耗尽区的宽度 W W W,顺便了解一下其内部的电场强度分布。
宽度W与内建电势、掺杂浓度的关系
为了求得宽度W与内建电势、掺杂浓度的关系,我们需要经历如下流程:
1.半导体的总电荷中性要求p侧每单位面积总负电荷必须精确地和n侧每单位面积总正空间电荷相等: N A ⋅ x p = N D ⋅ x n N_A\cdot x_p=N_D\cdot x_n NA⋅xp=ND⋅xn
p侧耗尽层宽度 x p x_p xp,n侧耗尽层宽度 x n x_n xn
由 x p , x n x_p,x_n xp,xn可以得到: 总耗尽层宽度 W = x p + x n 总耗尽层宽度W=x_p+x_n 总耗尽层宽度W=xp+xn
2.由泊松方程式引入两个已知的变量——掺杂浓度:KaTeX parse error: Expected 'EOF', got '}' at position 53: …ilon_s}(N_A-N_D}̲
,对上式积分两次,可以得到一个电势差。如果积分的区间合适,可以得到内建电势 V b i V_{bi} Vbi
3.第一次积分,得到耗尽层内的电场分布情况: E ( x ) = d ψ d x = { q N A ε s ( x + x p ) , − x p < x < 0 q N D ε s ( x − x n ) , 0 < x < x n E(x)=\frac{d\psi}{dx}=\begin{cases}\frac{qN_A}{\varepsilon_s}(x+x_p),-x_p<x<0\\ \\ \frac{qN_D}{\varepsilon_s}(x-x_n),0<x<x_n \end{cases} E(x)=dxdψ=⎩ ⎨ ⎧εsqNA(x+xp),−xp<x<0εsqND(x−xn),0<x<xn
绘制电场强度关于x的坐标轴:
由图可以得到电场强度在耗尽区内的最大值: E m = q N A x p ε s = q N D x n ε s E_m=\frac{qN_Ax_p}{\varepsilon_s}=\frac{qN_Dx_n}{\varepsilon_s} Em=εsqNAxp=εsqNDxn
4.第二次积分,可以得到耗尽区的内建电势 V b i V_{bi} Vbi: V b i = − ∫ − x p 0 E ( x ) d x − ∫ 0 x n E ( x ) d x = 1 2 E m W V_{bi}=-\int_{-x_p}^0 E(x)dx-\int_0^{x_n}E(x)dx=\frac{1}{2}E_mW Vbi=−∫−xp0E(x)dx−∫0xnE(x)dx=21EmW
对上式进行换算,可以得到宽度W关于内建电势的表达式: W = 2 V b i E m W=\frac{2V_{bi}}{E_m} W=Em2Vbi
5. E m E_m Em有两个表达式,分别采用了p侧的受主杂质和n侧的施主杂质。
为例同时使用p侧的受主杂质浓度和n侧的施主杂质浓度,我们对 W = 2 V b i E m W=\frac{2V_{bi}}{E_m} W=Em2Vbi进行变换: W = 2 V b i E m ⋅ 2 V b i E m W=\frac{\sqrt{2V_{bi}}}{\sqrt{E_m}} \cdot \frac{\sqrt{2V_{bi}}}{\sqrt{E_m}} W=Em2Vbi⋅Em2Vbi
将 E m = q N A x p ε s = q N D x n ε s E_m=\frac{qN_Ax_p}{\varepsilon_s}=\frac{qN_Dx_n}{\varepsilon_s} Em=εsqNAxp=εsqNDxn代入上式,得到: W = 2 ε s q ( 1 N D + 1 N A ) V b i = 2 ε s q ( N A + N D N A N D ) V b i W=\sqrt{\frac{2 \varepsilon_s}{q} (\frac{1}{N_D}+\frac{1}{N_A})V_{bi}}=\sqrt{\frac{2\varepsilon_s}{q}(\frac{N_A+N_D}{N_AN_D})V_{bi}} W=q2εs(ND1+NA1)Vbi=q2εs(NANDNA+ND)Vbi
突变结可以继续分类:当一边的掺杂浓度远大于另一边时,形成单边突变结
单边突变结
线性缓变结linearly graded junction
线性缓变结是深扩散或高能离子注入的pn结。
因此,当题目提及深扩散或高能离子注入式,则代入线性缓变结的知识点进行计算。
d V = d E ⋅ d W = d Q ε s d W = q ⋅ N ( E ) ⋅ d W 2 2 ε s dV=dE\cdot dW=\frac{dQ}{\varepsilon_s}dW=\frac{q\cdot N(E)\cdot dW^2}{2\varepsilon_s} dV=dE⋅dW=εsdQdW=2εsq⋅N(E)⋅dW2
分母中的“2”是因为电势施加后耗尽层两边都增厚了dW,所以要除以2吗
相关文章:

半导体器件与物理篇3 P-N结
热平衡时的PN结 pn结的定义:由p型半导体和n型半导体接触形成的结 pn结的特性和关键变量包括:整流性(即电流单向导通的特性)、平衡费米能级(费米能级 E F E_F EF为常数, d E F d x 0 )、内建电势 \frac…...

深入剖析String类的底层实现原理
嘿嘿,家人们,今天咱们来模拟实现string,好啦,废话不多讲,开干! 1:string.h 1.1:构造函数与拷贝构造函数 1.1.1:写法一 1.1.2:写法二(给缺省值) 1.2:赋值运算符重载与operatror[]获取元素 1.3:容量与迭代器 1.4:reserve与resize 1.5:清空与判断是否为空 1.6:push_back与…...

#其它:面试题
第一面试官提问如下: 1、自我介绍 2、根据项目提问:混合开发调取api的通讯方式 3、技术提问:如何隐藏div,但是div需要存在 使用 visibility 隐藏: 1.visibility: hidden2.display: none 3.opcity: 04、css塌陷问题…...

计算机视觉中的双边滤波:经典案例与Python代码解析
🌟 计算机视觉中的双边滤波:经典案例与Python代码解析 🚀 Hey小伙伴们!今天我们要聊的是计算机视觉中的一个重要技术——双边滤波。双边滤波是一种非线性滤波方法,主要用于图像去噪和平滑,同时保留图像的边…...

【AI日记】24.11.17 看 GraphRAG 论文,了解月之暗面
【AI论文解读】【AI知识点】【AI小项目】【AI战略思考】【AI日记】 核心工作 内容:看 GraphRAG 论文时间:4 小时评估:不错,继续 非核心工作 内容:了解国内大模型方向,重点了解了创业独角兽-月之暗面&…...
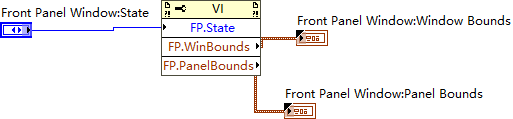
Front Panel Window Bounds 与 Front Panel Window Bounds 的区别与应用
在LabVIEW中,Front Panel Window Bounds 和 Front Panel WindowBounds 是两个不同的属性节点,用于描述前面板窗口的位置和大小。它们的区别主要体现在它们表示的是窗口的不同部分,具体如下: 1 Window Bounds:调整整个…...

比较TCP/IP和OSI/RM的区别
一、结构不同 1、OSI:OSI划分为7层结构:物理层、数据链路层、网络层、传输层、会话层、表示层和应用层。 2、TCP/IP:TCP/IP划分为4层结构:应用层、传输层、互联网络层和主机-网络层。 二、性质不同 1、OSI:OSI是制定…...

【Java项目】基于SpringBoot的【招聘信息管理系统】
技术简介:系统软件架构选择B/S模式、SpringBoot框架、java技术和MySQL数据库等,总体功能模块运用自顶向下的分层思想。 系统简介:招聘信息管理系统的功能分为管理员,用户和企业三个部分,系统的主要功能包括首页、个人中…...

【论文笔记】LLaMA-VID: An Image is Worth 2 Tokens in Large Language Models
🍎个人主页:小嗷犬的个人主页 🍊个人网站:小嗷犬的技术小站 🥭个人信条:为天地立心,为生民立命,为往圣继绝学,为万世开太平。 基本信息 标题: LLaMA-VID: An Image is W…...
使用Web Storage API实现客户端数据持久化
💓 博客主页:瑕疵的CSDN主页 📝 Gitee主页:瑕疵的gitee主页 ⏩ 文章专栏:《热点资讯》 使用Web Storage API实现客户端数据持久化 使用Web Storage API实现客户端数据持久化 使用Web Storage API实现客户端数据持久化…...

基于STM32F103的秒表设计-液晶显示
基于STM32F103的秒表设计-液晶显示 仿真软件: Proteus 8.17 编程软件: Keil 5 仿真实现: 在液晶1602上进行秒表显示,每100ms改变一次数值,一共三个按键,分为启动按键、暂停按键、复位按键。 电路介绍: 前面章节里已经和大家介绍了使用数码管设计的秒表,本次仿真将数…...

ReentrantLock的具体实现细节是什么
在 JDK 1.5 之前共享对象的协调机制只有 synchronized 和 volatile,在 JDK 1.5 中增加了新的机制 ReentrantLock,该机制的诞生并不是为了替代 synchronized,而是在 synchronized 不适用的情况下,提供一种可以选择的高级功能。 在 Java 中每个对象都隐式包含一个 monitor(监…...

【JavaScript】this 指向
1、this 指向谁 多数情况下,this 指向调用它所在方法的那个对象。即谁调的函数,this 就归谁。 当调用方法没有明确对象时,this 就指向全局对象。在浏览器中,指向 window;在 Node 中,指向 Global。&#x…...

DB Type
P位 p 1时段描述符有效,p 0时段描述符无效 Base Base被分成了三个部分,按照实际拼接即可 G位 如果G 0 说明描述符中Limit的单位是字节,如果是G 1 ,那么limit的描述的单位是页也就是4kb S位 S 1 表示代码段或者数据段描…...

python-返回函数
Python的函数不但可以返回int、str、list、dict等数据类型,还可以返回函数! 例如,定义一个函数 f(),我们让它返回一个函数 g,可以这样写: def f()ÿ…...

python语言基础-5 进阶语法-5.2 装饰器-5.2.1 闭包
声明:本内容非盈利性质,也不支持任何组织或个人将其用作盈利用途。本内容来源于参考书或网站,会尽量附上原文链接,并鼓励大家看原文。侵删。 5.2 装饰器 python中的装饰器相当于java中的注解。装饰器用于为函数添加某些修饰性、…...

用vscode编写verilog时,如何有信号定义提示、信号定义跳转(go to definition)、模块跳转(跨文件跳转)这些功能
(一)方法一:安装插件SystemVerilog - Language Support 安装一个vscode插件即可,插件叫SystemVerilog - Language Support。虽然说另一个插件“Verilog-HDL/SystemVerilog/Bluespec SystemVerilog”也有信号提示及定义跳转功能&am…...

MQTT+Springboot整合
1.mqttconfig配置(配置参数是从数据库查出来的) package com.terminal.dc3.api.center.manager.config;import com.collection.common.utils.StringUtils; import com.collection.system.mapper.MqttConfigMapper; import lombok.Data; import org.springframework.beans.fact…...

ERROR TypeError: AutoImport is not a function
TypeError: AutoImport is not a function 原因:unplugin-auto-import 插件版本问题 Vue3基于Webpack,在vue.config.js中配置 当unplugin-vue-components版本小于0.26.0时,使用以下写法 const { defineConfig } require("vue/cli-se…...

软考教材重点内容 信息安全工程师 第 3 章 密码学基本理论
(本章相对老版本极大的简化,所有与算法相关的计算全部删除,因此考试需要了解各个常 用算法的基本参数以及考试中可能存在的古典密码算法的计算,典型的例子是 2021 和 2022 年分别考了 DES 算法中的 S 盒计算,RSA 中的已…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...
