Leetcode 有效的数独

这段代码解决的是 验证一个数独是否有效 的问题,其算法思想是基于 规则校验和状态记录。具体思想如下:
算法思想
-
核心目标:
- 检查每个数字在 同一行、同一列 和 同一个 3x3 子格 中是否重复。
-
状态记录:
- 使用 3 个布尔二维数组分别记录:
- 每行数字的出现情况
rows[i][num]。 - 每列数字的出现情况
cols[j][num]。 - 每个 3x3 子格数字的出现情况
boxes[boxIndex][num]。
- 每行数字的出现情况
- 通过这些状态数组,可以快速检查某个数字是否在对应位置已存在。
- 使用 3 个布尔二维数组分别记录:
-
遍历与验证:
- 遍历整个 9x9 的数独表格,对于每一个非空格的数字:
- 计算数字对应的行、列和 3x3 子格索引。
- 检查当前数字是否在对应行、列或 3x3 子格中已存在。
- 如果存在,直接返回
false,表示数独无效。 - 如果不存在,将该数字标记为已出现,更新状态数组。
- 如果遍历完成未发现冲突,返回
true,表示数独有效。
- 遍历整个 9x9 的数独表格,对于每一个非空格的数字:
算法步骤
1. 初始化数据结构
- 定义三个布尔二维数组:
rows[9][9],cols[9][9],boxes[9][9]。rows[i][num]: 记录第i行中数字num+1是否已经出现。cols[j][num]: 记录第j列中数字num+1是否已经出现。boxes[boxIndex][num]: 记录第boxIndex个 3x3 子格中数字num+1是否已经出现。
2. 遍历整个数独表格
- 对于每个位置
(i, j):- 如果是空格(
'.'),直接跳过。 - 将字符数字转换为整数索引
num,如字符'5'转换为整数4(因为数组索引从0开始)。 - 计算数字所属的 3x3 子格索引:
boxIndex = (i / 3) * 3 + j / 3。- 行和列分别除以
3取整可以确定当前数字在哪一块 3x3 子格中。
- 行和列分别除以
- 如果是空格(
3. 检查并标记状态
- 检查状态数组:
- 如果
rows[i][num] == true,说明第i行已经出现过数字num+1。 - 如果
cols[j][num] == true,说明第j列已经出现过数字num+1。 - 如果
boxes[boxIndex][num] == true,说明该 3x3 子格已经出现过数字num+1。
- 如果
- 如果任何一项为
true,直接返回false。 - 否则,更新状态数组,将当前数字标记为已出现。
4. 返回结果
- 如果遍历完成,未发现任何冲突,则返回
true,表示数独有效。
关键点说明
1. 如何定位到 3x3 子格?
- 整个数独分为 9 个 3x3 子格:
子格索引: 0 1 2 3 4 5 6 7 8 - 每个数字的位置
(i, j)通过公式(i / 3) * 3 + j / 3定位到对应的子格索引。
2. 字符数字如何转换为数组索引?
- 数独中数字以字符形式存储,例如
'5'。 - 将其转为整数索引:
num = board[i][j] - '1'。'1'转换为索引0,'9'转换为索引8。
3. 为什么需要状态数组?
- 状态数组是为了快速记录和检查数字的存在性。
- 使用布尔值记录
true或false,可以节省时间复杂度,相较于遍历行、列和子格的直接检查更加高效。
时间和空间复杂度分析
-
时间复杂度:
- 遍历整个 9x9 表格,时间复杂度为 (O(9 \times 9) = O(81)),即常数级复杂度。
-
空间复杂度:
- 使用了 3 个 9x9 的布尔数组,总空间为 (3 \times 9 \times 9 = O(243)),即常数级复杂度。
总结
- 通过 遍历整个数独表格 和 使用状态数组记录数字的出现情况,有效避免了重复检查,算法逻辑清晰且高效。
- 算法充分利用了布尔数组在快速状态查询和标记上的优势,实现了对数独规则的校验。
class Solution {public boolean isValidSudoku(char[][] board) {boolean [][] rows = new boolean[9][9]; //rows[i][num]表示第i行是否出现过numboolean [][] cols = new boolean[9][9]; //cols[j][num]表示第j列是否出现过numboolean [][] boxes = new boolean[9][9]; //boxes[boxindex][num]表示第boxindex个3*3方格中是否出现过numfor(int i = 0; i < 9; i++) {for(int j = 0; j < 9; j++) {//首先跳过空格if(board[i][j] == '.') {continue;}//首先获取boxindexint boxindex = (i / 3) * 3 + (j / 3);//将字符数字转换为索引int num = board[i][j] - '1';if(rows[i][num] || cols[j][num] || boxes[boxindex][num]) {return false;}//然后标记rows[i][num] = true;cols[j][num] = true;boxes[boxindex][num] = true;}}return true;}
}
相关文章:

Leetcode 有效的数独
这段代码解决的是 验证一个数独是否有效 的问题,其算法思想是基于 规则校验和状态记录。具体思想如下: 算法思想 核心目标: 检查每个数字在 同一行、同一列 和 同一个 3x3 子格 中是否重复。 状态记录: 使用 3 个布尔二维数组分别…...

《Java核心技术 卷I》用户界面中首选项API
首选项API 在桌面程序中,通常都会存储用户首选项,如用户最后处理的文件、窗口的最后位置等。 利用Properties类可以很容易的加载和保存程序的配置信息,但有以下缺点: 有些操作系统没有主目录概念,很难为匹配文件找到…...

Android 中的 Zygote 和 Copy-on-Write 机制详解
在 Android 系统中,Zygote 是一个关键的进程,几乎所有的应用进程都是通过它 fork(派生)出来的。通过 Zygote 启动新进程的方式带来了显著的性能优势,这得益于 fork 操作和 Linux 中的 Copy-on-Write(COW&am…...

【人工智能】从零开始用Python实现逻辑回归模型:深入理解逻辑回归的原理与应用
解锁Python编程的无限可能:《奇妙的Python》带你漫游代码世界 《Python OpenCV从菜鸟到高手》带你进入图像处理与计算机视觉的大门! 逻辑回归是一种经典的统计学习方法,用于分类问题尤其是二分类问题。它通过学习数据的特征和目标标签之间的…...
推荐一款功能强大的光学识别OCR软件:Readiris Dyslexic
Readiris Dyslexic是一款功能强大的光学识别OCR软件,可以扫描任何纸质文档并将其转换为完全可编辑的数字文件(Word,Excel,PDF),然后用你喜欢的编辑器进行编辑。该软件提供了一种轻松创建,修改和签名PDF的完整解决方法&…...

Python爬虫----python爬虫基础
一、python爬虫基础-爬虫简介 1、现实生活中实际爬虫有哪些? 2、什么是网络爬虫? 3、什么是通用爬虫和聚焦爬虫? 4、为什么要用python写爬虫程序 5、环境和工具 二、python爬虫基础-http协议和chrome抓包工具 1、什么是http和https协议…...

css-50 Projects in 50 Days(3)
html <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>旋转页面</title><link rel"sty…...

另外一种缓冲式图片组件的用法
文章目录 1. 概念介绍2. 使用方法2.1 基本用法2.2 缓冲原理3. 示例代码4. 内容总结我们在上一章回中介绍了"FadeInImage组件"相关的内容,本章回中将介绍CachedNetworkImage组件.闲话休提,让我们一起Talk Flutter吧。 1. 概念介绍 我们在本章回中介绍的CachedNetwo…...

字节青训-小C的外卖超时判断、小C的排列询问
目录 一、小C的外卖超时判断 问题描述 测试样例 解题思路: 问题理解 数据结构选择 算法步骤 最终代码: 运行结果: 二、小C的排列询问 问题描述 测试样例 最终代码: 运行结果: 编辑 一、小C的外卖超时判断…...

PHP 伪静态详解及实现方法
概述 在现代 Web 开发中,URL 的设计对用户体验和搜索引擎优化(SEO)至关重要。动态 URL 虽然功能强大,但往往显得冗长且不友好。伪静态(URL 重写)技术通过将动态 URL 转换为静态样式,不仅提高了…...

Spring Boot 简单预览PDF例子
目录 前言 一、引入依赖 二、使用步骤 1.创建 Controller 处理 PDF 生成和预览 2.创建预览页面 总结 前言 使用 Spring Boot 创建一个生成 PDF 并进行预览的项目,你可以按以下步骤进行。我们将使用 Spring Boot、Thymeleaf、iText 等技术来完成这个任务。 一、引入…...

【魔珐有言-注册/登录安全分析报告-无验证方式导致安全隐患】
前言 由于网站注册入口容易被机器执行自动化程序攻击,存在如下风险: 暴力破解密码,造成用户信息泄露,不符合国家等级保护的要求。短信盗刷带来的拒绝服务风险 ,造成用户无法登陆、注册,大量收到垃圾短信的…...
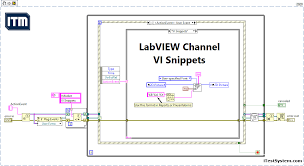
LabVIEW 使用 Snippet
在 LabVIEW 中,Snippet(代码片段) 是一个非常有用的功能,它允许你将 一小段可重用的代码 保存为一个 图形化的代码片段,并能够在不同的 VI 中通过拖放来使用。 什么是 Snippet? Snippet 就是 LabVIEW 中的…...

单片机_day3_GPIO
目录 1. 灯如何才能亮 1.1原理图 1.2 二极管 1.3 换了一个灯和原理图 编辑 1.4 三极管 1.4.1 NPN型三极管 1.4.2 PNP型三极管 2. 基本概念 3. 输入 3.1 浮空输入 3.2 上拉输入 3.3 下拉输入 3.4 模拟输入 4. 输出 4.1 推挽输出 4.2 开漏输出 如何让开漏输出…...

Python小游戏24——小恐龙躲避游戏
首先,你需要安装Pygame库。如果你还没有安装,可以通过以下命令安装: 【bash】 pip install pygame 【python】代码 import pygame import random # 初始化Pygame pygame.init() # 设置屏幕尺寸 screen_width 800 screen_height 600 screen …...

Python 的多态笔记
Python的多态实际是通过instance 实现的 class Person:def __init__(self, name,age):self.name nameself.age agedef feed_pet(self,pet):#isinastance(obj,类)-->判断obj,是不是这个类的对象,或者判断obj是不是该类的子类的对象if isinstance(pet, Pet):sel…...

go module使用
go module介绍 go module是go官⽅⾃带的go依赖管理库,在1.13版本正式推荐使⽤ go module可以将某个项⽬(⽂件夹)下的所有依赖整理成⼀个 go.mod ⽂件,⾥⾯写⼊了依赖的版本等 使⽤ go module之后我们可不⽤将代码放置在src下了 使⽤ go module 管理依赖后会在项⽬根⽬录下⽣成…...

c ++零基础可视化——数组
c 零基础可视化 数组 一些知识: 关于给数组赋值,一个函数为memset,其在cplusplus.com中的描述如下: void * memset ( void * ptr, int value, size_t num );Sets the first num bytes of the block of memory pointed by ptr to…...

CVE-2024-2961漏洞的简单学习
简单介绍 PHP利用glibc iconv()中的一个缓冲区溢出漏洞,实现将文件读取提升为任意命令执行漏洞 在php读取文件的时候可以使用 php://filter伪协议利用 iconv 函数, 从而可以利用该漏洞进行 RCE 漏洞的利用场景 PHP的所有标准文件读取操作都受到了影响࿱…...

计算机组成原理笔记----基础篇
计算机系统硬件软件 软件 ├── 系统软件 │ ├── 操作系统 │ └── 工具软件 └── 应用软件├── 办公软件├── 媒体软件└── 浏览器软件硬件 ├── 计算机硬件 │ ├── 中央处理器(CPU) │ ├── 存储设备 │ │ ├── …...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...
