精华帖分享｜浅谈金融时间序列分析与股价随机游走

本文来源于量化小论坛公共讨论区板块精华帖，作者为正扬，发布于2024年6月3日。

以下为精华帖正文：

01

引

时间序列分析是个很唬人的术语，实际上它也不是一个很容易接近的话题。我本科曾经短暂地学过一点点，又看到互联网上存在许多关于时许分析的操作谬误，因此特写本文给大家一些好上手的理解方式。

时间序列分析是统计学的一个分支，它旨在研究有时间顺序的数据，探索其内在结构和特性，从而进行描述、建模、预测和控制。而统计学作为一门核心科学，时序分析也继承其科学性，有很强的逻辑性。反映到具体实操场景，就是用户对使用的模型必须有清楚的认知，否则即使模型提供了预测值，也不知道如何使用。

在这里，我就以量化中最常见的股价/币价，来说明使用时序分析时你一定会遇到的种种困难（和可能的解法）。本文无法一语道破如何预测股价，只是希望揭开时间序列分析的面纱，让你感觉不再陌生。

02

时间序列

首先讲讲时间序列的分类，因为时序不仅仅在金融数据中使用，也在各行各业中广泛应用。销售数据、气象信息和GDP都是时间序列。下面这张图就说明了时间序列的多种变化，分别是周期性（房屋销售额存在时长和频率不确定的高低起伏），季节性（电力产值的冬夏两季的规律波动），趋势性（国债价格随天数增加而下降）和随机性（谷歌的股价波动）。图片中的数据其实包含多种时间序列性质，有兴趣的读者可以尝试从中再分离一种明显性质，具体答案见链接原文。

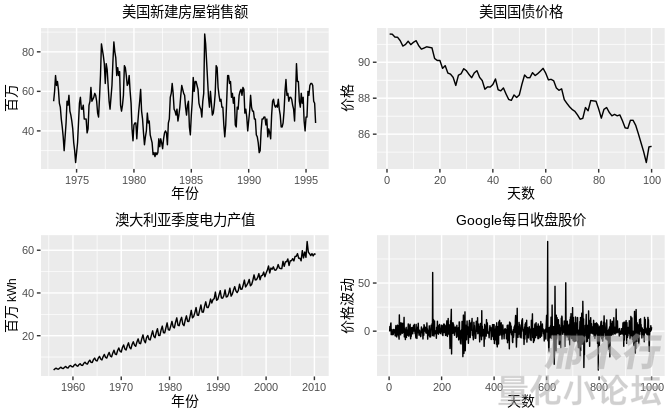
来源：https://otexts.com/fppcn/tspatterns.html

只要是按照时间顺序排列的离散数据都可以成为时间序列，而有了序列我们就可以对数据作统计分析，得到其均值（期望）和方差（二阶矩）。若对时间序列分类，则有平稳时间序列和非平稳时间序列。一般而言，我们对平稳的时间序列更有兴趣，因为从字面理解，平稳则意味着我们可以推断规律。（如果想探索更严谨的定义，请自行搜索严格平稳和广义平稳）。当然，平稳并不一定代表一定有规律可推断，这一点在后面也会着重说明。

看到这里你已经知道，时间序列分析所需要的数据其实是非常苛刻的，而且上述图片的四种数据都不是平稳数据。回想一下，你是否曾经把这些原始数据放进时序模型里面去尝试建模呢？

03

金融时间序列

那我们不妨用大饼数据来看看，究竟如何处理价格走势，使其符合时间序列分析的要求。本章的所有技术细节你都可以跳过，只要看加粗的结论就行。

首先，我们有一张btc-usdt.csv，里面包含的close收盘价和volume成交量是我们的目标。先处理close，我们的做法是取其对数收益率。这样做有两个好处，首先相比百分比收益率，对数收益率可加；其次可以形成一个公式，yt=yt−1+Δyt.这个递推公式赋予了其推理逻辑。于是我们就把问题转化为：只要能预测Δyt,我们就可以预测整个价格的走势了。

大饼小时线收盘价（暴涨暴跌，非常不平稳，作为新手请凭感觉理解）

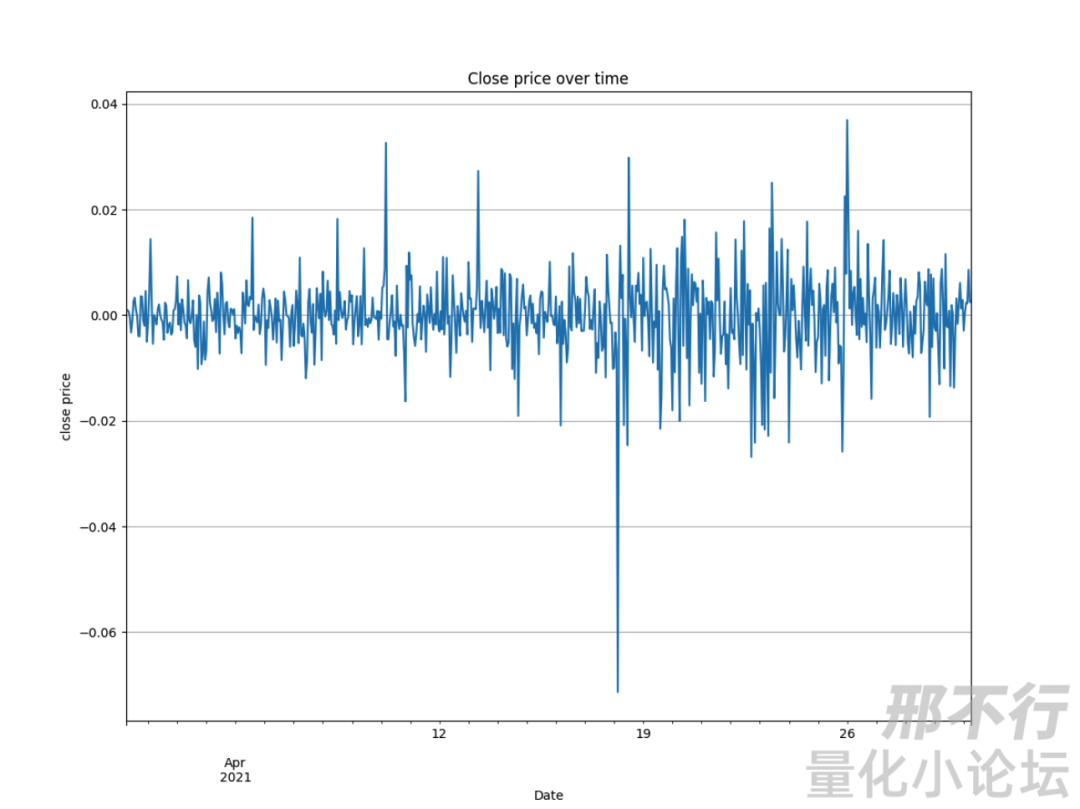
大饼对数收益率（相比收盘价，是不是大多数都集中在0之间？这样就看起来平稳多了）

如果你想了解测试时序平稳性的工具，请搜索Augmented Dickey–Fuller test. 以下结果可能需要至少本科概率论与数理统计的知识去理解。（别忘了问chatgpt辅助理解）这里的结果提示这个序列是平稳的。

ADF Test Results:
ADF Statistic: -14.11980992097059
p-value: 2.4361396630638024e-26
Critical Values:
1%: -3.439835148993393
5%: -2.865725696693157
10%: -2.568998987353403
Used lag: 3
Number of observations used: 692

1、随机游走

我们认为这个序列是一个平稳序列，但是不是就可以开始建模预测了呢？并非如此。

前文提到，平稳并不一定代表一定有规律可推断，因为白噪声也算是一种平稳。白噪声是完全随机的数据，统计学上是一个正态分布，没有任何算法可以告诉你下一个随机数是多少。前文中我们提到股价可以表示为yt=yt−1+Δyt，如果Δyt是白噪声，那么yt就是在前一期的值上再加一个随机数，请问它是能预测的吗？很明显，不行，这个模型也被称为随机游走(random walking)，你能想到的布朗运动就是RW在二维空间中的形式。那么股价是随机游走吗？不幸的是，很大概率是的。 要验证股价随机游走，必须祭出统计学工具。这里我们会用到Ljung-Box Q检验，辅助自相关函数图作直观展示。

首先看Ljung-Box Q，其p值大于0.05，这意味着我们不能以 95% 的置信水平拒绝原假设，认为没有足够的证据说明时间序列不是白噪声。（此段需理解数理统计中的假设检验部分。）

Lungbox Test Results:
lb_stat lb_pvalue
10 18.05919 0.053973

2、自相关函数

我们用另一个更直观的方式看：自相关函数。它表示某时刻的数据与其前n项数据的自相关关系。第一根柱表示，它与自身的相关性为1，从第二项开始相关性迅速降为0左右，在置信区间内，说明它与其滞后项没有自相关。因此我们大致判定，这个数列是一个白噪声数列。我们没有办法用时间序列去推测btc-usdt的未来走势。

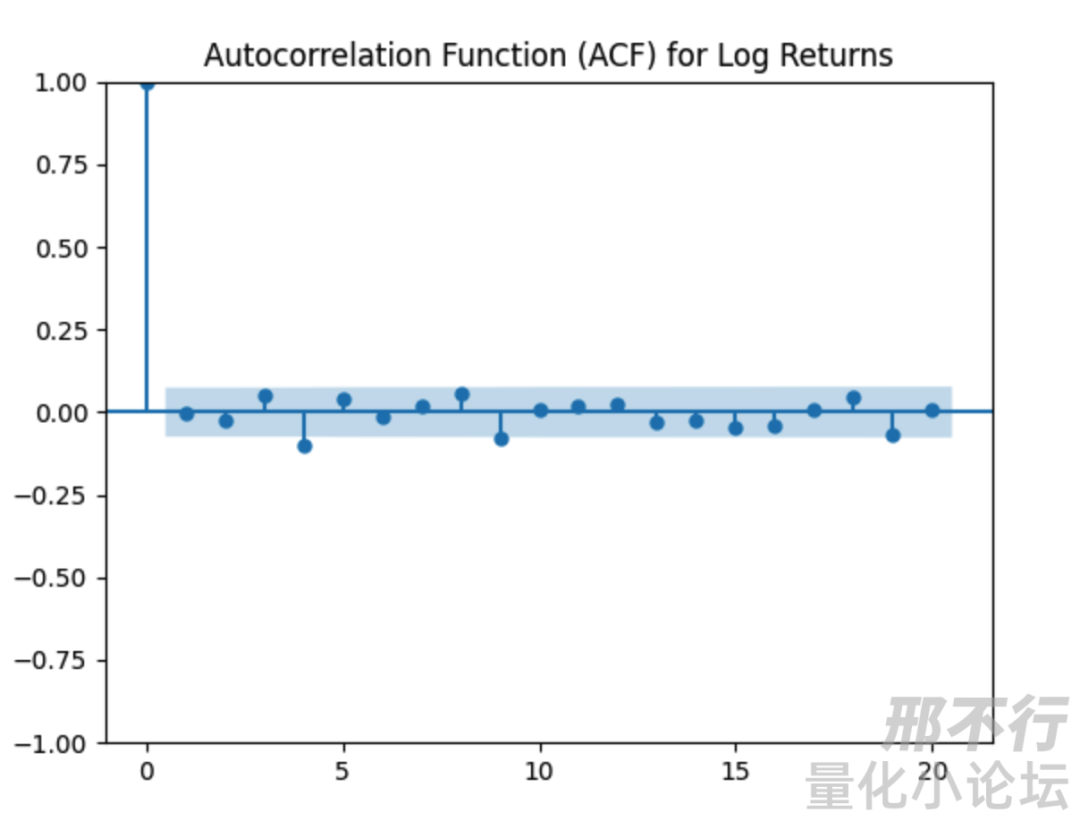
04

模型

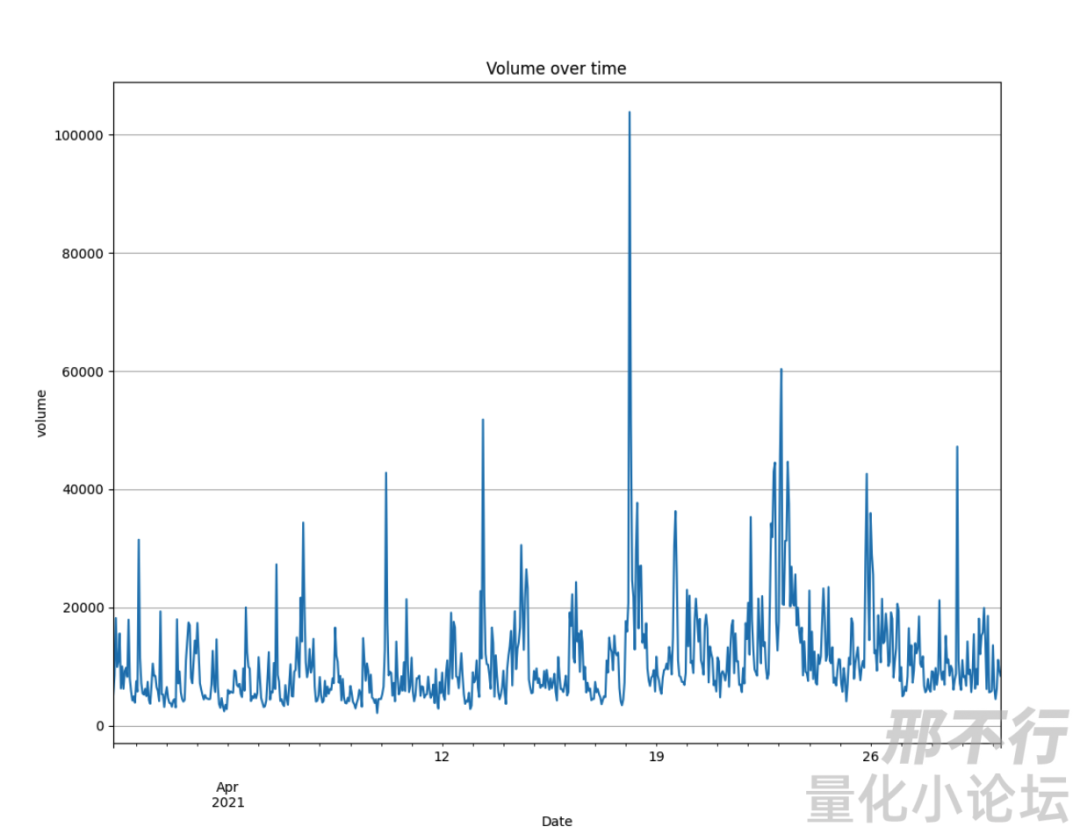
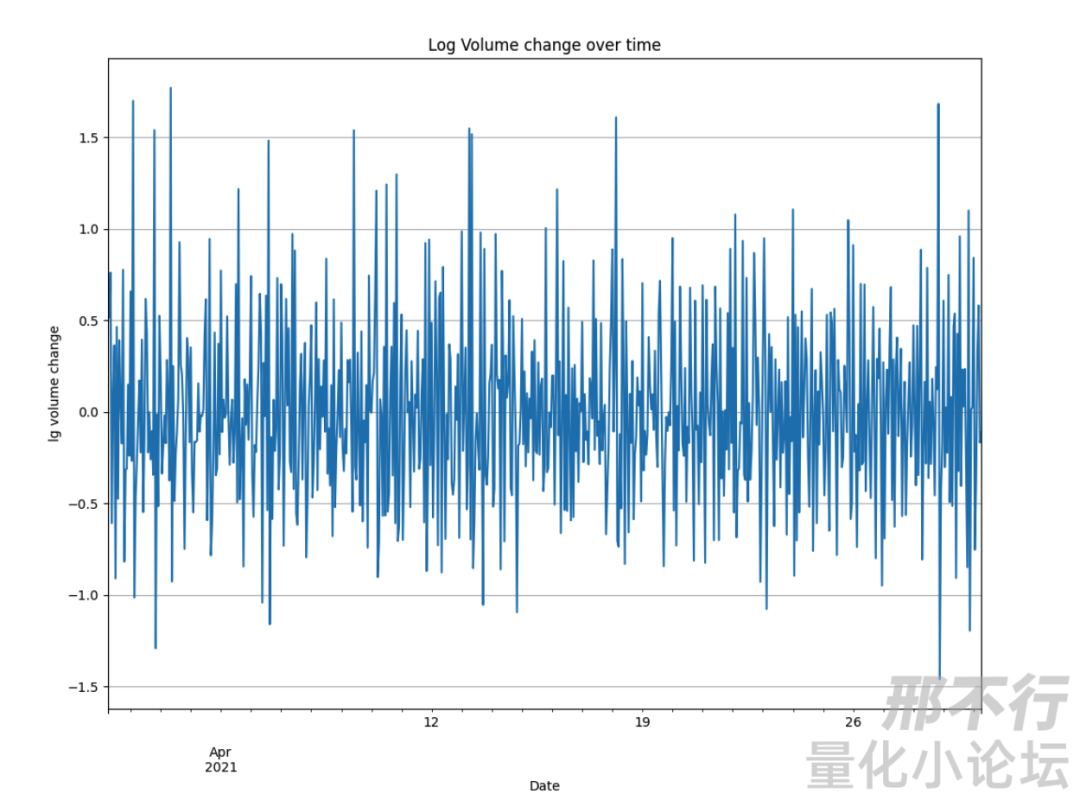
这里就可以看出它的原值就包含很强的周期性特征了。我们进一步分析：

ADF Test Results:
ADF Statistic: -10.56484687260585
p-value: 7.563340881893284e-19
Critical Values:
1%: -3.439974756130998
5%: -2.865787205712192
10%: -2.569031757724822
Used lag: 13
Number of observations used: 682

ADF检验表明该序列是平稳序列。这个结论和随机游走模型相同。

Ljungbox Test Results:
lb_stat lb_pvalue
10 90.340146 4.585370e-1

Ljung Box Q检验表明p value接近0，远小于0.05，因此拒绝该序列为白噪声。说明这个数列是有时序关系的。

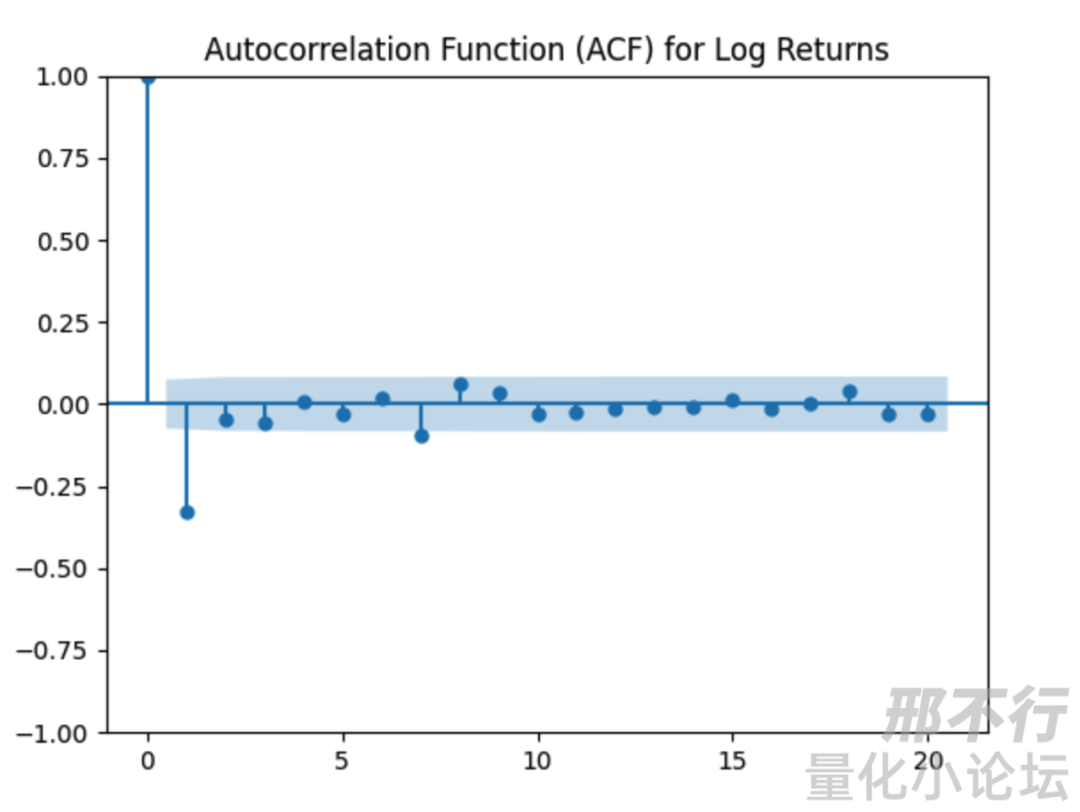
ACF图表明，当前项与滞后1项存在负的自相关关系，即滞后1期正值则当期大概率负值，即该小时放量则下个小时更可能缩量。

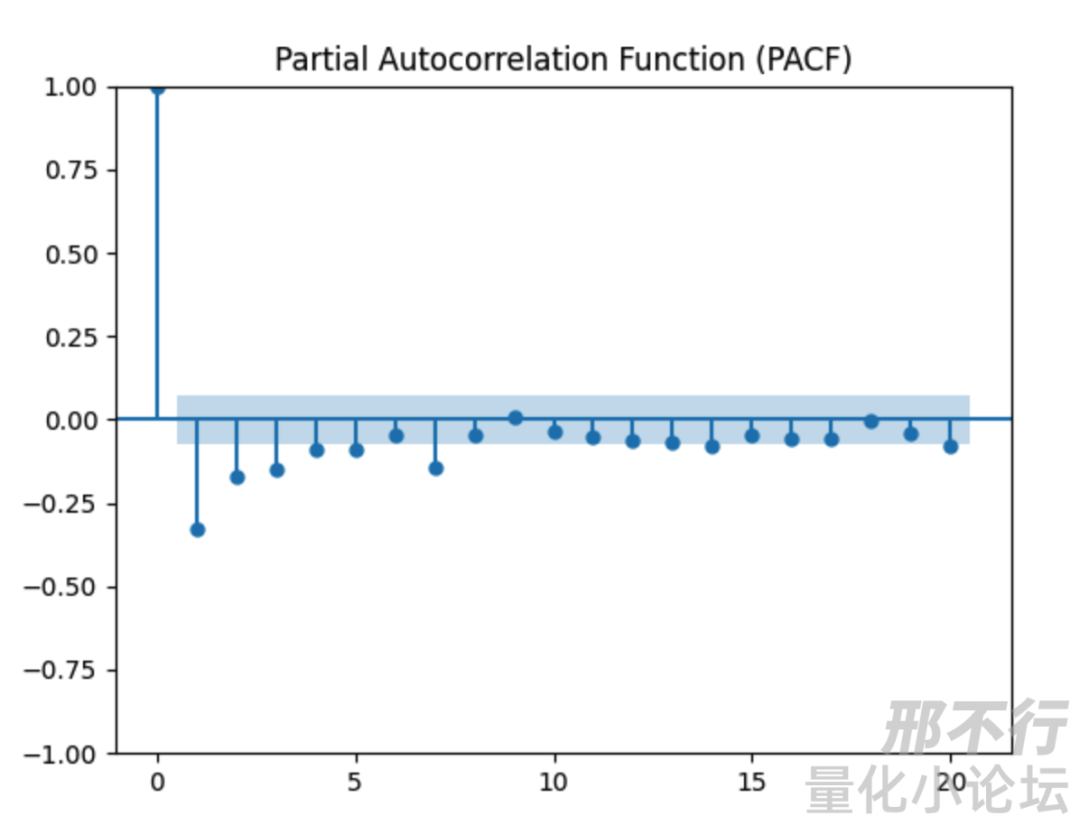
Partial ACF图，用于判断ARMA模型阶数，这里不展开，具体可问chatgpt。

1、建模过程

接下来我们就进入建模过程了，由以上ACF和PACF图推断，我们使用ARMA(1,1)模型。

输出模型结果：

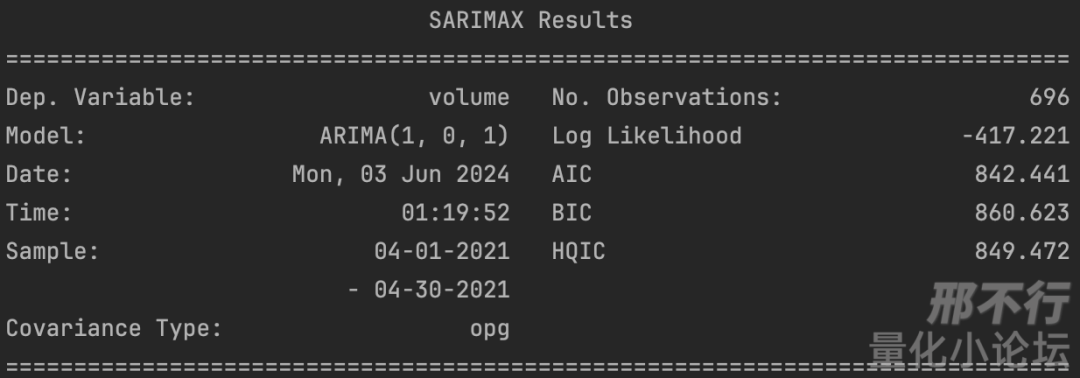
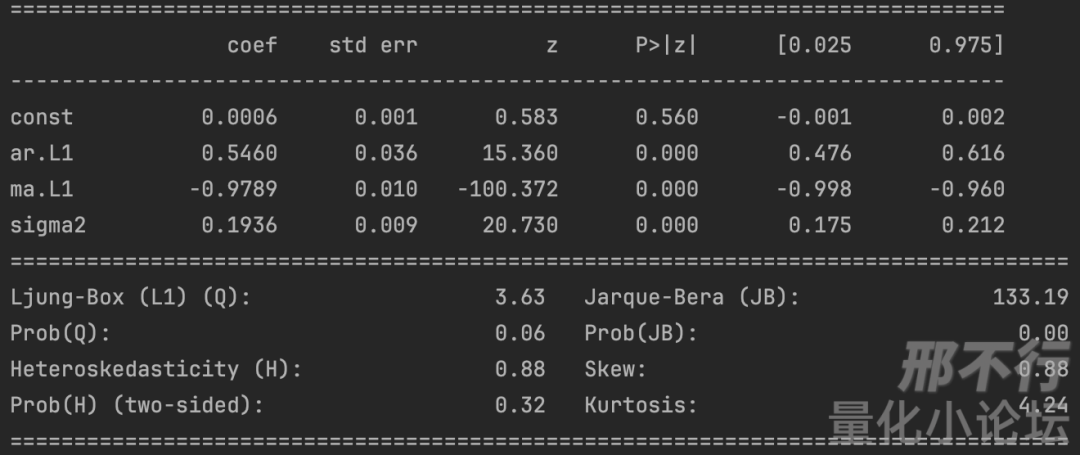
所以这个时间序列ARMA(1,1)的模型即为yt=0.0006+0.5460yt−1+ϵt−0.9789ϵt−1.

此外，关注模型的诊断数据，Ljung-Box在此检测残差，发现p值大于0.05，提示残差不含时序特征，说明我们成功提取了时间序列特征。Heteroskedasticity检测波动，也不显著。最后Jarque-Bera检测提示残差分布显著偏离正态分布，可能需要在预测时加以修正。

2、预测

基于这个结果，我们可以对未来数据进行预测了。但是请问，此处可以预测未来多少期数据？我的答案是1期，最多两2期。因为超出这个限度，我们会基于我们的预测值再去预测未来（别忘了ACF函数只有1期自相关关系），会导致误差显著增大。

以下是预测的结果：

2021-04-30 07:00:00 0.085933

05

结语

到此，我们就做完了对某个时间序列的对数变化率的时间序列分析。我一直认为时间序列模型是一个工具，但时间序列分析是一门科学。工具可以对任何正确格式的输入都产生一个结果，但你需要用科学和逻辑去分析这个结果的合理性，否则这个结果只能图一乐。

本文有许多不详尽之处，有的是想照顾看热闹的朋友从而写得更直白一些，有的可能是我真的已经忘了QAQ。如大佬们发现错误欢迎在评论区指正。

最后祝大家都能写代码赚大钱！^^