【AI系统】核心计算之矩阵乘
核心计算之矩阵乘
AI 模型中往往包含大量的矩阵乘运算,该算子的计算过程表现为较高的内存搬移和计算密度需求,所以矩阵乘的效率是 AI 芯片设计时性能评估的主要参考依据。本文我们一起来看一下矩阵乘运算在 AI 芯片的具体过程,了解它的执行性能是如何被优化实现的。
从卷积到矩阵乘
AI 模型中的卷积层的实现定义大家应该都已经比较熟悉了,卷积操作的过程大概可以描述为按照约定的窗口大小和步长,在 Feature Map 上进行不断地滑动取数,窗口内的 Feature Map 和卷积核进行逐元素相乘,再把相乘的结果累加求和得到输出 Feature Map 的每个元素结果。卷积到矩阵乘的的转换关系示意如下图。

其中逐元素相乘,再累加的过程就是上节提到的一个计算单位:MACs,矩阵乘的 MACs 数对最终性能具有重要影响。通过将输入数据(Feature Map)和卷积核数据进行重排,卷积操作本质上可以等效理解为矩阵乘操作。
假设卷积的输入和输出的特征图维度用(IH, IW), (OH, OW)表示,卷积核窗口的数据维度用(KH, KW)表示,输入通道是 IC,输出通道是 OC,输入输出特征图和卷积核数据维度重排的转化对应关系如下公式,对输入数据的重排的过程称为 Im2Col,同理把转换后矩阵乘的数据排布方式再换回卷积输入的过程称为 Col2Im。
i n p u t : ( I C , I H , I W ) → ( O H ∗ O W , K H ∗ K W ∗ I C ) f i l t e r : ( O C , K H , K W , I C ) → ( O C , K H ∗ K W ∗ I C ) o u t p u t : ( O C , O H , O W ) → ( O C , O H ∗ O W ) \begin{align} &input:(IC, IH, IW)\rightarrow(OH*OW, KH*KW*IC)\\ &filter: (OC, KH, KW, IC)\rightarrow(OC, KH*KW*IC)\\ &output:(OC,OH, OW)\rightarrow(OC,OH*OW) \end{align} input:(IC,IH,IW)→(OH∗OW,KH∗KW∗IC)filter:(OC,KH,KW,IC)→(OC,KH∗KW∗IC)output:(OC,OH,OW)→(OC,OH∗OW)
更具体的,假设卷积核的维度(2, 2),输入特征图维度(3, 3),输入和输出通道都是 1,对一个无 padding,stride=1 的卷积操作,输出特征图是(2, 2),所以输入卷积核转换为矩阵乘排布后的行数是 2 ∗ 2 = 4 2 * 2 = 4 2∗2=4,列数为 2 ∗ 2 ∗ 1 = 4 2 * 2 * 1= 4 2∗2∗1=4。下图是对应的卷积到矩阵乘的转换示意,输入、输出特征图和卷积核都用不同的颜色表示,图中数字表示位置标记。

比如输入特征图的排布转换过程:第 1 个输出对应输入特征图的窗口数据标记为 1, 2, 4, 5;第 2 个输出对应的输入特征图窗口数据标记为 2, 3, 5, 6;第 3 个输出对应的输入特征图窗口数据标记为 4, 5, 7, 8;第 4 个输出对应的输入特征图窗口数据标记为 5, 6, 8, 9。矩阵乘的维度对应关系如下。
i n p u t : ( O H ∗ O W , K H ∗ K W ∗ I C ) → ( 4 , 4 ) f i l t e r : ( O C , K H ∗ K W ∗ I C ) → ( 1 , 4 ) o u t p u t : ( O C , O H ∗ O W ) → ( 1 , 4 ) \begin{align} &input: (OH*OW, KH*KW*IC)\rightarrow (4,4)\\ &filter: (OC, KH*KW*IC)\rightarrow(1,4)\\ &output:(OC, OH*OW)\rightarrow(1,4) \end{align} input:(OH∗OW,KH∗KW∗IC)→(4,4)filter:(OC,KH∗KW∗IC)→(1,4)output:(OC,OH∗OW)→(1,4)
矩阵乘分块 Tilling
上面介绍了卷积到矩阵乘的转换过程,我们可以发现,转换后的矩阵乘的维度非常大,而芯片里的内存空间往往是有限的(成本高),表现为越靠近计算单元,带宽越快,内存越小。为了平衡计算和内存加载的时间,让算力利用率最大化,AI 芯片往往会进行由远到近,多级内存层级的设计方式,达到数据复用和空间换时间的效果。根据这样的设计,矩阵乘实际的数据加载和计算过程将进行分块 Tiling 处理。
假设用 CHW 表示上面转换公式中的 K H ∗ K W ∗ I C KH * KW * IC KH∗KW∗IC 的值,M 表示 OC,N 表示 $OH * OW $,矩阵乘的输入特征图维度是 (CHW, N),矩阵乘的卷积核维度是(M, CHW),输出矩阵维度是(M, N),可以同时在 M,N,CHW 三个维度进行 Tiling,每次计算过程分别加载一小块的特征图和卷积核数据计算,比如在 M,N,CHW 三个维度各分了 2 小块,得到完成的输出特征图需要进行 8 次的数据加载和计算。下图中的 Step1, Step2 展示了两次数据加载可以完成一个输出 Tile 块的计算过程。

矩阵乘的库
矩阵乘作为 AI 模型中的重要性能算子,CPU 和 GPU 的平台上都有专门对其进行优化实现的库函数。比如 CPU 的 OpenBLAS, Intel MKL 等,GPU 的 cuBLAS, cuDNN 等。实现的方法主要有 Loop 循环优化 (Loop Tiling)和多级缓存 (Memory Hierarchy)。
其两者的实现逻辑大概分为如下 2 步,关于 Kernel 实现优化的技术细节在[推理引擎]章节进一步展开。
- Lib 感知相乘矩阵的 Shape
- 选择最优的 Kernel 实现来执行
下图展示了对矩阵乘进行 Loop 循环优化和多级缓存结合的实现流程。
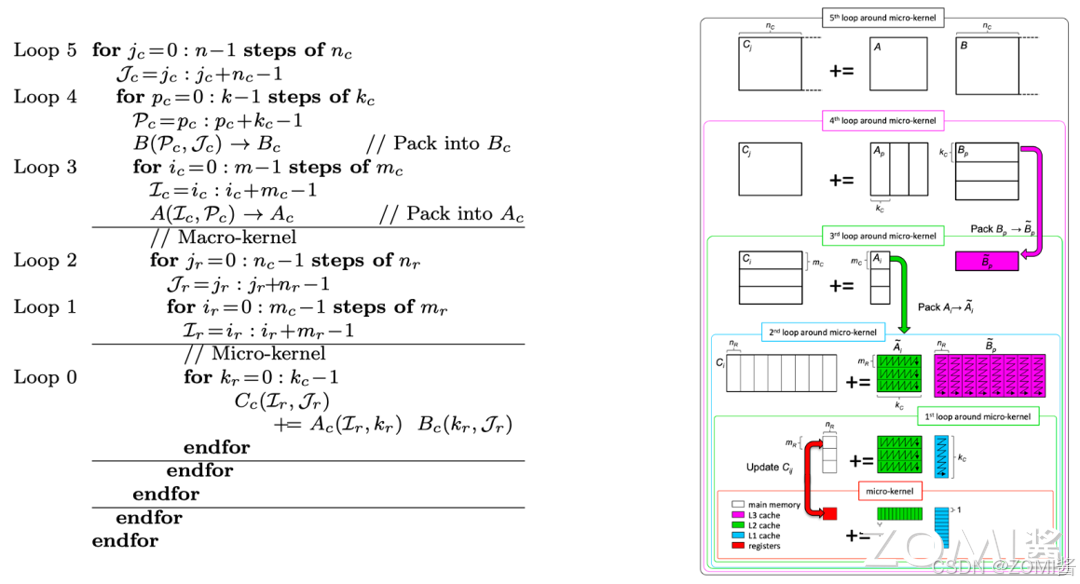
左边是共 6 级 Loop 循环展开的伪代码,右边是 Loop 对应多级存储的数据 Tilling 和搬移过程,假设矩阵乘 A,B,C 对应维度是(m, k, n)。
- Loop5, Loop4, Loop3 对应把矩阵在 n, k, m 维度进行 Tilling 的切分,Tilling 后维度大小分别是 nc, kc, mc。
- Loop2, Loop1 分别将 Tilling 后的 nc, mc 维度再一次 Tilling,Tilling 后维度大小分别是 nr, mr。
- Loop0 对 kc 维度进行展开,实现累加求和的过程,得到(mr, nr)大小输出矩阵的部分和。
图中不同的颜色框指代了在不同存储层级上的数据计算,不同颜色块表示该块数据的存储位置。结合不同存储层级的内存空间和数据搬移带宽大小,将不同大小的 A,B 矩阵的 Tilling 块放在不同的存储层级上,可以平衡 AI 芯片执行矩阵乘任务时的时间和空间开销,提升整体算力利用率。比如,对(mr, nr)的计算过程,通过将 B 矩阵的(kc,nr)加载 1 次到 L1 cache 中,每次从 L2 cache 加载 A 矩阵的(mr, kc)大小到计算模块,进行计算,假设 mc 切分了 3 个 mr,则 B 矩阵的(kc, nr)就在 L1 中被重复利用了 3 次。这种用空间换时间或者用时间换空间的策略是进行算子性能优化的主要方向。
矩阵乘的优化
矩阵乘作为计算机科学领域的一个重要基础操作,有许多优化算法可以提高其效率。下面我们对常见的矩阵乘法优化算法做一个整体的归类总结。
-
基本的循环优化:通过调整循环顺序、内存布局等手段,减少缓存未命中(cache miss)和数据依赖,提高缓存利用率,从而加速矩阵乘法运算。
-
分块矩阵乘法(Blocked Matrix Multiplication):将大矩阵划分成小块,通过对小块矩阵进行乘法运算,降低了算法的时间复杂度,并能够更好地利用缓存。
-
SIMD 指令优化:利用单指令多数据(SIMD)指令集,如 SSE(Streaming SIMD Extensions)和 AVX(Advanced Vector Extensions),实现并行计算,同时处理多个数据,提高计算效率。
-
SIMT 多线程并行化:利用多线程技术,将矩阵乘法任务分配给多个线程并行执行,充分利用多核处理器的计算能力。
-
算法改进:如 Fast Fourier Transform 算法,Strassen 算法、Coppersmith-Winograd 算法等,通过矩阵分解和重新组合,降低了算法的时间复杂度,提高了计算效率。
这些优化算法通常根据硬件平台、数据规模和计算需求选择不同的策略,以提高矩阵乘法运算的效率。在具体的 AI 芯片或其它专用芯片里面,对矩阵乘的优化实现主要就是减少指令开销,可以表现为两个方面:
-
**让每个指令执行更多的 MACs 计算。**比如 CPU 上的 SIMD/Vector 指令,GPU 上的 SIMT/Tensor 指令,NPU 上 SIMD/Tensor,Vector 指令的设计。
-
**在不增加内存带宽的前提下,单时钟周期内执行更多的 MACs。**比如英伟达的 Tensor Core 中支持低比特计算的设计,对每个 cycle 执行 512bit 数据的带宽前提下,可以执行 64 个 8bit 的 MACs,大于执行 16 个 32bit 的 MACs。
如果您想了解更多AI知识,与AI专业人士交流,请立即访问昇腾社区官方网站https://www.hiascend.com/或者深入研读《AI系统:原理与架构》一书,这里汇聚了海量的AI学习资源和实践课程,为您的AI技术成长提供强劲动力。不仅如此,您还有机会投身于全国昇腾AI创新大赛和昇腾AI开发者创享日等盛事,发现AI世界的无限奥秘~
相关文章:

【AI系统】核心计算之矩阵乘
核心计算之矩阵乘 AI 模型中往往包含大量的矩阵乘运算,该算子的计算过程表现为较高的内存搬移和计算密度需求,所以矩阵乘的效率是 AI 芯片设计时性能评估的主要参考依据。本文我们一起来看一下矩阵乘运算在 AI 芯片的具体过程,了解它的执行性…...

Vue.js 自定义指令:从零开始创建自己的指令
vue使用directive 前言vue2使用vue3使用 前言 关于使用自定义指令在官网中是这样描述的 vue2:对普通 DOM 元素进行底层操作,这时候就会用到自定义指令。 vue3:自定义指令主要是为了重用涉及普通元素的底层 DOM 访问的逻辑。 在 Vue.js 中使用自定义指令…...

策略模式
定义:即定义一系列的算法,算法1,算法2,...,算法n,把他们封装起来,使他们可以相互替换。 优点:使得一个类的行为或者其算法可以在运行时改变,而且使用Context类的人在外部…...

性能优化--CPU微架构
一 指令集架构 Intel X86, ARM v8, RISC-V 是当今广泛使用的指令架构的实例。 大多数现代架构可以归类为基于通用寄存器的加载和存储型架构,在这种架构下,操作数倍明确指定,只能使用夹在和存储指令访问内存。除提供基本的功能之外,…...

在 Sanic 框架中实现高效内存缓存的多种方法
在使用 Sanic 框架开发 Web 应用时,我们可以通过内存缓存来提升应用的性能,减少对数据库或其他外部服务的频繁请求。下面提供一些在 Sanic 中实现内存缓存的基本方法。 使用 Python 内置的 functools.lru_cache 如果你的缓存需求比较简单,且…...

Mac 环境变量配置基础教程
MacOS 下一般配置有多个 Shell,如 Bash、ZSH 等,不同的 Shell 其创建 Terminal 时使用的环境变量配置文件也不尽相同,但一般都会读取并执行脚本文件 /etc/profile 来加载系统级环境变量,而用户级别环境变量,一般都会在…...
自动折叠功能)
Qt如何屏蔽工具栏(QToolBar)自动折叠功能
最近发现Qt上工具栏一行放不下的时候,会自动折叠起来。当用户点击展开功能的小三角按钮时,工具栏会展开成多行。这个功能本身没什么问题,但是当工具栏展开的时候,鼠标光标一旦不小心移动到了工具栏外面,这时候…...

【数据分享】中国统计摘要(1978-2024)
数据介绍 《中国统计摘要(1978 - 2024)》犹如一部浓缩的历史巨著,承载着中国几十年来的发展轨迹与辉煌成就。它是由国家统计局精心编纂的重要资料,为我们全方位地展现了中国在经济、社会、民生等各个领域的深刻变革。 这本统计摘…...
unity运行状态下移动、旋转、缩放控制模型
demo地址:https://download.csdn.net/download/elineSea/90017272 unity2021以上版本用下面的插件 https://download.csdn.net/download/elineSea/90017305...

《 C++ 点滴漫谈 一 》C++ 传奇:起源、演化与发展
摘要 C 是一门兼具高效性与灵活性的编程语言,自上世纪 80 年代诞生以来,已经深刻影响了计算机科学与技术的发展。从 Bjarne Stroustrup 的初步构想到如今遍布各大领域,C 经历了语言规范的不断完善与功能的持续扩展。本文详细回顾了 C 的起源…...
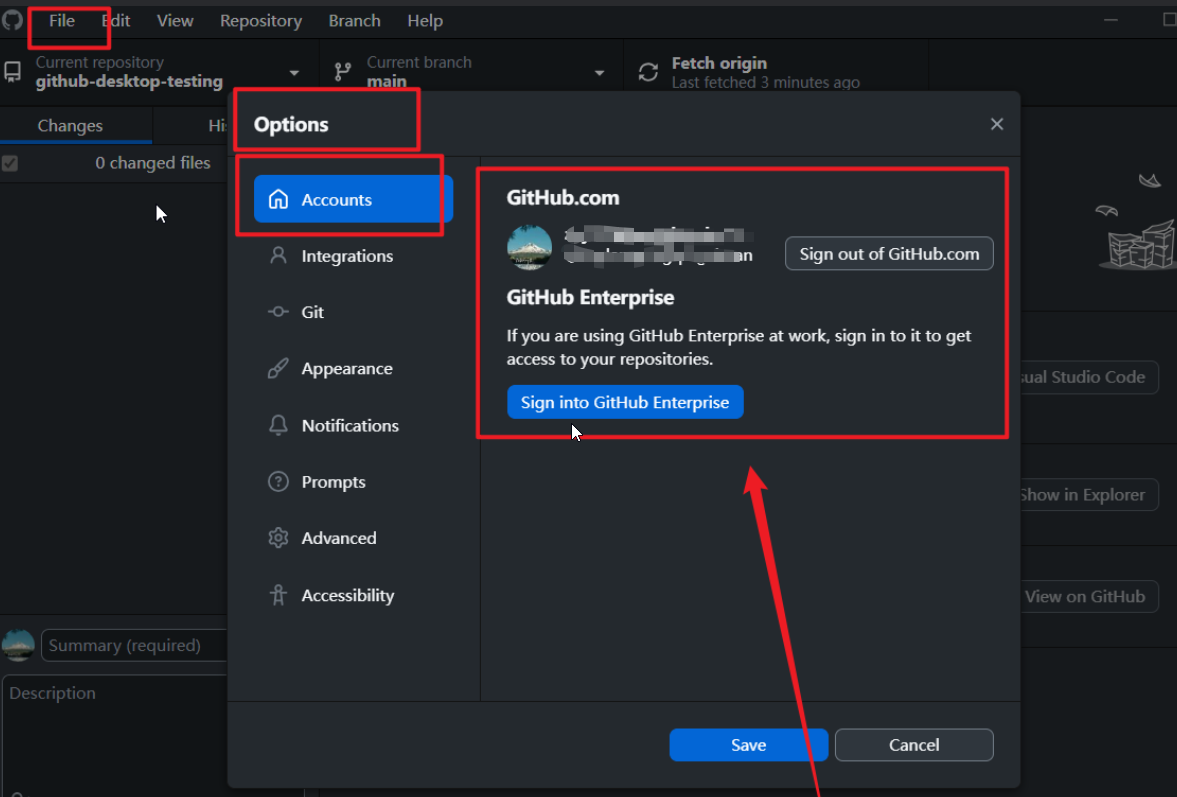
Github客户端工具github-desktop使用教程
文章目录 1.客户端工具的介绍2.客户端工具使用感受3.仓库的创建4.初步尝试5.本地文件和仓库路径5.1原理说明5.2修改文件5.3版本号的说明5.4结合码云解释5.5版本号的查找 6.分支管理6.1分支的引入6.2分支合并6.3创建测试仓库6.4创建测试分支6.5合并分支6.6合并效果查看6.7分支冲…...

自然语言处理:第六十三章 阿里Qwen2 2.5系列
本人项目地址大全:Victor94-king/NLP__ManVictor: CSDN of ManVictor 项目地址: QwenLM/Qwen2.5: Qwen2.5 is the large language model series developed by Qwen team, Alibaba Cloud. 官网地址: 你好,Qwen2 | Qwen & Qwen2.5: 基础模型大派对&a…...

springboot中设计基于Redisson的分布式锁注解
如何使用AOP设计一个分布式锁注解? 1、在pom.xml中配置依赖 <dependency><groupId>org.springframework</groupId><artifactId>spring-aspects</artifactId><version>5.3.26</version></dependency><dependenc…...

C++初阶学习第十一弹——list的用法和模拟实现
目录 一、list的使用 二.list的模拟实现 三.总结 一、list的使用 list的底层是双向链表结构,双向链表中每个元素存储在互不相关的独立节点中,在节点中通过指针指向 其前一个元素和后一个元素。 常见的list的函数的使用 std::list<int> It {1,…...

共享单车管理系统项目学习实战
前言 Spring Boot Vue前后端分离 前端:Vue(CDN) Element axios(前后端交互) BaiDuMap ECharts(图表展示) 后端:Spring Boot Spring MVC(Web) MyBatis Plus(数据库) 数据库:MySQL 验证码请求...

详细解读TISAX汽车信息安全评估
TISAX汽车信息安全评估是一个针对汽车行业的信息安全评估和交换机制,以下是对其的详细解读: 一、背景与目的 TISAX是在德国汽车工业协会(VDA)的支持下开发的,旨在确保跨公司边界的汽车行业信息安全评估的认可度&…...
)
gitlab cicd搭建及使用笔记(二)
cicd之gitlab-runner使用要点 官方链接:https://docs.gitlab.com/runner/ 附历史文章链接 https://blog.csdn.net/qq_42936727/article/details/143624523?spm1001.2014.3001.5501 gitlab-runner常用命令及解释 gitlab-runner verify 容器内,检查注…...

鸿蒙实战:页面跳转传参
文章目录 1. 实战概述2. 实现步骤2.1 创建鸿蒙项目2.2 编写首页代码2.3 新建第二个页面 3. 测试效果4. 实战总结 1. 实战概述 本次实战,学习如何在HarmonyOS应用中实现页面间参数传递。首先创建项目,编写首页代码,实现按钮跳转至第二个页面并…...
)
Spring Security SecurityContextHolder(安全上下文信息)
在本篇博客中,我们将讨论 Spring Security 的 SecurityContextHolder 组件,包括其实现方式、关键特性,并通过实际示例进行说明。 理解 SecurityContextHolder SecurityContextHolder 是 Spring Security 存储当前安全上下文详细信息的地方。…...

蓝队技能-应急响应篇日志自动采集日志自动查看日志自动化分析Web安全内网攻防工具项目
知识点: 1、应急响应-系统日志收集-项目工具 2、应急响应-系统日志查看-项目工具 3、应急响应-日志自动分析-项目工具 演示案例-蓝队技能-工具项目-自动日志采集&自动日志查看&自动日志分析 系统日志自动采集-观星应急工具(Windows系统日志) SglabIr_Co…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...
