蓝桥杯每日真题 - 第18天
题目:(出差)
题目描述(13届 C&C++ B组E题)


解题思路:
-
问题分析
-
问题实质是一个带权图的最短路径问题,但路径的权重包含两个部分:
-
从当前城市到下一个城市的路程时间。
-
当前城市的离开时间。
-
-
需要计算从城市1到城市N的最短时间。
-
-
图的表示
-
用邻接矩阵表示图,将不存在的边初始化为无穷大。
-
-
路径规划
-
使用Dijkstra算法,从城市1开始,动态更新到其他城市的最短路径时间。
-
-
特殊处理
-
起点城市(城市1)的离开时间
staytime[0]设为0,因为小明可以直接出发。
-
-
时间复杂度
-
Dijkstra的时间复杂度为 O(N2)O(N^2)O(N2) (由于使用邻接矩阵实现),在节点数较小时仍然可行。
-

代码实现(C语言):
#define maxn 1001
#define inf INT_MAX
#define edgetype int#include <stdio.h>
#include <stdlib.h>
#include <limits.h>void initedges(edgetype graph[maxn][maxn], int n)
{int i, j;for (i = 0; i < n; i++){for (j = 0; j < n; j++){graph[i][j] = inf;}}
}void addedges(edgetype graph[maxn][maxn], int u, int v, int w)
{if (graph[u][v] == inf || w < graph[u][v]){graph[u][v] = w;}if (graph[v][u] == inf || w < graph[v][u]){graph[v][u] = w;}
}void dijkstra(edgetype graph[maxn][maxn], int s, int n, edgetype dist[maxn], edgetype staytime[maxn])
{int visited[maxn];int i;for (i = 0; i < n; i++){dist[i] = inf;visited[i] = 0;}dist[s] = 0;while (1){int minindex = -1;int min = inf;for (int i = 0; i < n; i++){if (!visited[i] && dist[i] < min) {min = dist[i];minindex = i;}}if (min == inf){break;}visited[minindex] = 1;for (i = 0; i < n; i++){int u = graph[minindex][i];if (visited[i]){continue;}if (u == inf){continue;}if (dist[i] == inf || dist[i] > min + u + staytime[i]){dist[i] = min + u + staytime[i];}}}
}int main(int argc, char *argv[])
{int N, M, i, u, v, w;edgetype staytime[maxn], graph[maxn][maxn], dist[maxn];scanf("%d %d", &N, &M);for (i = 0; i < N; i++){scanf("%d", &staytime[i]);}staytime[0] = 0;initedges(graph, N);for (i = 0; i < M; i++){scanf("%d %d %d", &u, &v, &w);addedges(graph, u - 1, v - 1, w);}dijkstra(graph, 0, N, dist, staytime);printf("%d", dist[N - 1] - staytime[N - 1]);return 0;
}得到运行结果:

代码分析:
-
图的初始化
-
initedges函数将图中所有的边权值初始化为无穷大(inf),表示没有直接连通的路径。
-
-
添加边
-
addedges函数会将边(u, v)及其权值w加入到邻接矩阵中,同时判断是否已有更短路径,如果有就更新。
-
-
Dijkstra算法
-
核心部分是
dijkstra函数:-
使用一个
visited数组标记已确定最短路径的节点。 -
每次找到当前未访问节点中距离起点最近的节点。
-
松弛操作:尝试更新所有相邻节点的最短距离,考虑路径花费和目标节点的离开时间。
-
-
-
输入输出
-
输入部分:城市数量
N、道路数量M、每个城市离开时间以及M条双向边信息。 -
输出部分:从起点城市
1到终点城市N的最短时间。
-
-
重要逻辑
-
在
dijkstra中更新距离时,将离开时间加入权值计算:dist[i] = min + u + staytime[i]。
-
难度分析
⭐️⭐️⭐️⭐️⭐️难难难难难急急急急急急急
总结
本代码解决了一个加权图中的特殊最短路径问题,考虑到离开时间的影响。
它适用于小型的城市网络,提供了可靠的解法。
相关文章:

蓝桥杯每日真题 - 第18天
题目:(出差) 题目描述(13届 C&C B组E题) 解题思路: 问题分析 问题实质是一个带权图的最短路径问题,但路径的权重包含两个部分: 从当前城市到下一个城市的路程时间。 当前城市的…...

HTTP 协议应用场景
一、HTTP 协议简介 HTTP(Hypertext Transfer Protocol)即超文本传输协议,是用于分布式、协作式和超媒体信息系统的应用层协议,是互联网数据通信的基础。它采用客户端 - 服务器(Client-Server)的通信模式&am…...

【Linux庖丁解牛】—Linux基本指令(下)!
目录 1、grep指令 2、zip/unzip指令 3、sz/rz指令 4、tar指令 编辑 5、scp指令 6、bc指令 7、uname –r指令 8、重要的几个热键 9、关机 10、完结撒花 1、grep指令 grep是文本过滤器,其作用是在指定的文件中过滤出包含你指定字符串的内容,…...

python: generator model using sql server 2019
設計或生成好數據庫,可以生成自己設計好的框架項目 # encoding: utf-8 # 版权所有 :2024 ©涂聚文有限公司 # 许可信息查看 :言語成了邀功盡責的功臣,還需要行爲每日來值班嗎 # 描述: : 生成实体 # Author …...

Kafka怎么发送JAVA对象并在消费者端解析出JAVA对象--示例
1、在pom.xml中加入依赖 <dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-stream-kafka</artifactId><version>3.1.6</version></dependency> 2、配置application.yml 加入Kafk…...
)
深度学习(1)
一、torch的安装 基于直接设备情况,选择合适的torch版本,有显卡的建议安装GPU版本,可以通过nvidia-smi命令来查看显卡驱动的版本,在官网中根据cuda版本,选择合适的版本号,下面是安装示例代码 GPUÿ…...
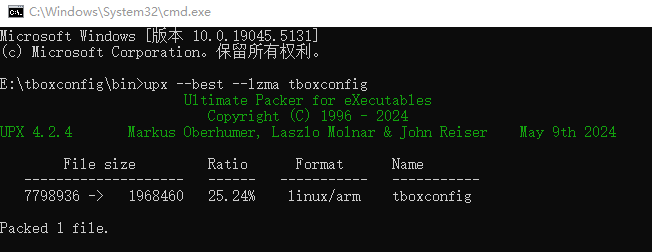
golang 嵌入式armv7l压缩编译打包
编译 Go 应用程序 go build -ldflags"-s -w" -o myapp.exe . 使用 UPX 压缩可执行文件(window下载并设置环境变量) upx --best --lzma myapp.exe 可从10M压缩到1M 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 …...

Makefile 之 join
join $(join <list1>,<list2> ) 名称:连接函数——join。 功能:把<list2>中的单词对应地加到<list1>的单词后面。如果<list1>的单词个数要比<list2>的多, 那么,<list1>中的多出…...

集合卡尔曼滤波(Ensemble Kalman Filter),用于二维滤波(模拟平面上的目标跟踪),MATLAB代码
集合卡尔曼滤波(Ensemble Kalman Filter) 文章目录 引言理论基础卡尔曼滤波集合卡尔曼滤波初始化预测步骤更新步骤卡尔曼增益更新集合 MATLAB 实现运行结果3. 应用领域结论 引言 集合卡尔曼滤波(Ensemble Kalman Filter, EnKF)是…...

北京申请中级职称流程(2024年)
想找个完整详细点的申请流程资料真不容易,做个分享送给需要的人吧。 不清楚为什么说文章过度宣传,把链接和页面去掉了,网上自己找一下。 最好用windows自带的EDGE浏览器打开申请网站,只有在开始申请的时间内才可以进行网上申报&…...

ubuntu.24安装cuda
1.下载CUDA Toolkit https://developer.nvidia.com/cuda-toolkit-archive 2.按照命令下载,安装 sudo sh cuda_12.2.2_535.104.05_linux.run 3.环境变量 sudo vi /etc/profile 最后面添加 export PATH“/usr/local/cuda-12.2/bin: P A T H " e x p o r t L D L…...

unity li2cpp逆向原理是什么?
主要涉及将Unity游戏引擎中的C#代码转换为C代码,并进一步编译为各平台的原生(Native)代码的过程,以及逆向工程工具如何利用这一过程中的特定文件来还原和分析原始代码。以下是对Unity IL2CPP逆向原理的详细解释: 对惹…...

Python网络爬虫实践案例:爬取猫眼电影Top100
以下是一个Python网络爬虫的实践案例,该案例将演示如何使用Python爬取猫眼电影Top100的电影名称、主演和上映时间等信息,并将这些信息保存到TXT文件中。此案例使用了requests库来发送HTTP请求,使用re库进行正则表达式匹配,并包含详…...

卷积神经网络(CNN)中的权重(weights)和偏置项(bias)
在卷积神经网络(CNN)中,权重(weights)和偏置项(bias)是两个至关重要的参数,它们在网络的学习和推断过程中起着关键作用。 一、权重(Weights) 1. 定义…...

华为FusionCube 500-8.2.0SPC100 实施部署文档
环境: 产品:FusionCube 500版本:8.2.0.SPC100场景:虚拟化基础设施平台:FusionCompute两节点 MCNA * 2硬件部署(塔式交付场景)免交换组网(配置AR卡) 前置准备 组网规划 节…...
OKHttp网络通信)
Android 网络请求(二)OKHttp网络通信
学习笔记 OkHttp 是一个非常强大且流行的 HTTP 客户端库,广泛用于 Android 开发中进行网络请求。与 HttpURLConnection 相比,OkHttp 提供了更简单、更高效的 API,特别是在处理复杂的 HTTP 请求时。 如何使用 OkHttp 进行网络请求 以下是使…...

npm上传自己封装的插件(vue+vite)
一、npm账号及发包删包等命令 若没有账号,可在npm官网:https://www.npmjs.com/login 进行注册。 在当前项目根目录下打开终端命令窗口,常见命令如下: 1、登录命令:npm login(不用每次都重新登录࿰…...
如何在Word文件中设置水印以及如何禁止修改水印
在日常办公和学习中,我们经常需要在Word文档中设置水印,以保护文件的版权或标明文件的机密性。水印可以是文字形式,也可以是图片形式,能够灵活地适应不同的需求。但仅仅设置水印是不够的,有时我们还需要确保水印不被随…...

.NET桌面应用架构Demo与实战|WPF+MVVM+EFCore+IOC+DI+Code First+AutoMapper
目录 .NET桌面应用架构Demo与实战|WPFMVVMEFCoreIOCDICode FirstAutoPapper技术栈简述项目地址:功能展示项目结构项目引用1. 新建模型2. Data层,依赖EF Core,实现数据库增删改查3. Bussiness层,实现具体的业务逻辑4. Service层&am…...

el-table根据指定字段合并行和列+根据屏幕高度实时设置el-table的高度
文章目录 html代码script代码arraySpanMethod.js代码 html代码 <template><div class"rightBar"><cl-table ref"tableData"border :span-method"arraySpanMethod" :data"tableData" :columns"columns":max-…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...
