算法【子数组最大累加和问题与扩展】
子数组最大累加和问题是一个非常经典的问题,也比较简单。但是扩展出的问题很多,在笔试、面试中特别常见,扩展出的问题很多非常有趣,解法也比较巧妙。
下面通过一些题目来加深理解。
题目一
测试链接:https://leetcode.cn/problems/maximum-subarray/
分析:这是一道常见且较为简单的题,下面给出严格位置依赖和空间压缩的解法。代码如下。
class Solution {
public:int dp[100000];int maxSubArray(vector<int>& nums) {int length = nums.size();int ans = nums[0];dp[0] = nums[0];for(int i = 1;i < length;++i){dp[i] = dp[i-1] >= 0 ? dp[i-1] + nums[i] : nums[i];ans = ans > dp[i] ? ans : dp[i];}return dp[length-1];}
};下面是空间压缩的解法。代码如下。
class Solution {
public:int maxSubArray(vector<int>& nums) {int length = nums.size();int cur, last;int ans = nums[0];last = nums[0];for(int i = 1;i < length;++i){cur = last >= 0 ? last + nums[i] : nums[i];ans = ans > cur ? ans : cur;last = cur;}return ans;}
};题目二
测试链接:https://leetcode.cn/problems/house-robber/
分析:这相当于是一个不能取相邻数的最大数组累加和的题。可以构造二维dp数组dp[i][0]代表以i为结尾,不偷下标为i的房屋的最大金额,dp[i][1]代表以i为结尾,偷下标为i的房屋的最大金额。代码如下。
class Solution {
public:int dp[100][2];int rob(vector<int>& nums) {int length = nums.size();int ans = nums[0];dp[0][0] = 0;dp[0][1] = nums[0];for(int i = 1;i < length;++i){dp[i][0] = dp[i-1][0] > dp[i-1][1] ? dp[i-1][0] : dp[i-1][1];ans = ans > dp[i][0] ? ans : dp[i][0];dp[i][1] = dp[i-1][0] + nums[i];ans = ans > dp[i][1] ? ans : dp[i][1];}return ans;}
};下面是空间压缩的解法。代码如下。
class Solution {
public:int rob(vector<int>& nums) {int length = nums.size();int ans = nums[0];int last_no = 0, last_yes = nums[0];int cur_no, cur_yes;for(int i = 1;i < length;++i){cur_no = last_no > last_yes ? last_no : last_yes;ans = ans > cur_no ? ans : cur_no;cur_yes = last_no + nums[i];ans = ans > cur_yes ? ans : cur_yes;last_no = cur_no;last_yes = cur_yes;}return ans;}
};题目三
测试链接:https://leetcode.cn/problems/maximum-sum-circular-subarray/
分析:对于环形数组求子数组的最大和有两种情况,一种是最大子数组就是非环形数组求最大子数组的结果,另一种是子数组跨过了开头和结尾。对于第一种情况,正常求数组的最大子数组即可。对于第二种情况,只需求数组的最小子数组,然后用数组的总和减去最小子数组。两种情况取最大值即是答案。代码如下。
class Solution {
public:int dp1[30001];int dp2[30001];int maxSubarraySumCircular(vector<int>& nums) {int length = nums.size();int ans1 = nums[0], ans2 = nums[0], all = nums[0];dp1[0] = nums[0];dp2[0] = nums[0];for(int i = 1;i < length;++i){all += nums[i];dp1[i] = dp1[i-1] >= 0 ? dp1[i-1] + nums[i] : nums[i];ans1 = ans1 > dp1[i] ? ans1 : dp1[i];dp2[i] = dp2[i-1] > 0 ? nums[i] : dp2[i-1] + nums[i];ans2 = ans2 < dp2[i] ? ans2 : dp2[i];}return ans2 == all ? ans1 : ans1 > all - ans2 ? ans1 : all - ans2;}
};下面是空间压缩的解法。代码如下。
class Solution {
public:int last_1, cur_1;int last_2, cur_2;int maxSubarraySumCircular(vector<int>& nums) {int length = nums.size();int ans1 = nums[0], ans2 = nums[0], all = nums[0];last_1 = nums[0];last_2 = nums[0];for(int i = 1;i < length;++i){all += nums[i];cur_1 = last_1 >= 0 ? last_1 + nums[i] : nums[i];ans1 = ans1 > cur_1 ? ans1 : cur_1;cur_2 = last_2 > 0 ? nums[i] : last_2 + nums[i];ans2 = ans2 < cur_2 ? ans2 : cur_2;last_1 = cur_1;last_2 = cur_2;}return ans2 == all ? ans1 : ans1 > all - ans2 ? ans1 : all - ans2;}
};
题目四
测试链接:https://leetcode.cn/problems/house-robber-ii/
分析:对于这种环形的情况,依然是分了两种情况,第一种情况是不偷下标为0的房子,第二种情况是偷下标为0的房子。这两种情况最后求出来四个值取最大即是答案。代码如下。
class Solution {
public:int dp1[101][2];int dp2[101][2];int get_max(int a, int b, int c, int d){int ans = a;ans = ans > b ? ans : b;ans = ans > c ? ans : c;ans = ans > d ? ans : d;return ans;}int rob(vector<int>& nums) {int length = nums.size();if(length == 1){return nums[0];}if(length == 2){return nums[0] > nums[1] ? nums[0] : nums[1];}dp1[1][0] = 0;dp1[1][1] = nums[1];for(int i = 2;i < length;++i){dp1[i][0] = dp1[i-1][0] > dp1[i-1][1] ? dp1[i-1][0] : dp1[i-1][1];dp1[i][1] = dp1[i-1][0] + nums[i];}dp2[2][0] = 0;dp2[2][1] = nums[2];for(int i = 3;i < length-1;++i){dp2[i][0] = dp2[i-1][0] > dp2[i-1][1] ? dp2[i-1][0] : dp2[i-1][1];dp2[i][1] = dp2[i-1][0] + nums[i];}return get_max(dp1[length-1][0], dp1[length-1][1], dp2[length-2][0]+nums[0], dp2[length-2][1]+nums[0]);}
};下面是空间压缩的版本。代码如下。
class Solution {
public:int last_1_no, last_1_yes, cur_1_no, cur_1_yes;int last_2_no, last_2_yes, cur_2_no, cur_2_yes;int get_max(int a, int b, int c, int d){int ans = a;ans = ans > b ? ans : b;ans = ans > c ? ans : c;ans = ans > d ? ans : d;return ans;}int rob(vector<int>& nums) {int length = nums.size();if(length == 1){return nums[0];}if(length == 2){return nums[0] > nums[1] ? nums[0] : nums[1];}if(length == 3){return nums[0] > nums[1] ? nums[0] > nums[2] ? nums[0] : nums[2] : nums[1] > nums[2] ? nums[1] : nums[2];}last_1_no = 0;last_1_yes = nums[1];for(int i = 2;i < length;++i){cur_1_no = last_1_no > last_1_yes ? last_1_no : last_1_yes;cur_1_yes = last_1_no + nums[i];last_1_no = cur_1_no;last_1_yes = cur_1_yes;}last_2_no = 0;last_2_yes = nums[2];for(int i = 3;i < length-1;++i){cur_2_no = last_2_no > last_2_yes ? last_2_no : last_2_yes;cur_2_yes = last_2_no + nums[i];last_2_no = cur_2_no;last_2_yes = cur_2_yes;}return get_max(last_1_no, last_1_yes, last_2_no+nums[0], last_2_yes+nums[0]);}
};题目五
测试链接:https://leetcode.cn/problems/house-robber-iv/
分析:这道题可以想到二分答案法。因为窃取能力的范围是有限的,只需要使用二分搜索对窃取能力是否能偷盗至少k间房屋进行判断,即可得到最小窃取能力。代码如下。
class Solution {
public:int last_no, last_yes, cur_no, cur_yes;int f(int ability, vector<int>& nums, int length){last_no = 0;last_yes = nums[0] <= ability ? 1 : 0;for(int i = 1;i < length;++i){cur_no = last_no > last_yes ? last_no : last_yes;cur_yes = nums[i] <= ability ? last_no + 1 : last_no;last_no = cur_no;last_yes = cur_yes; }return last_no > last_yes ? last_no : last_yes;}int get_max(vector<int>& nums, int length){int ans = nums[0];for(int i = 1;i < length;++i){ans = ans > nums[i] ? ans : nums[i];}return ans;}int minCapability(vector<int>& nums, int k) {int length = nums.size();int l = 0, r, middle, ans;r = get_max(nums, length);while (l < r){middle = l + (r - l) / 2;if(f(middle, nums, length) >= k){r = middle - 1;ans = middle;}else{l = middle + 1;}}return ans;}
};题目六
测试链接:https://leetcode.cn/problems/max-submatrix-lcci/
分析:这个就是子数组求最大累加和拓展了一个维度。首先,对于不同数量不同行的组合,在相同下标上的值求和得到一个一维数组。对这个一维数组求子数组最大累加和找到最大的答案记录坐标即可。遍历即可得到答案。代码如下。
class Solution {
public:int last, last_start, cur, cur_start, ans, ans_start, ans_end;int f(vector<int> &nums, int length){last = nums[0];last_start = 0;ans = nums[0];ans_start = 0;ans_end = 0;for(int i = 1;i < length;++i){cur = last > 0 ? last + nums[i] : nums[i];cur_start = last > 0 ? last_start : i;if(cur > ans){ans = cur;ans_start = cur_start;ans_end = i;}last = cur;last_start = cur_start;}return ans;}vector<int> getMaxMatrix(vector<vector<int>>& matrix) {int r1, c1, r2, c2;vector<int> Ans;Ans.assign(4, 0);int maxValue = (1 << 31);int value;int row = matrix.size();int column = matrix[0].size();int add;vector<int> temp;temp.assign(column, 0);for(int i = 0;i < row;++i){for(int j = i;j < row;++j){for(int index = 0;index < column;++index){add = 0;for(int begin = i;begin <= j;++begin){add += matrix[begin][index];}temp[index] = add;}value = f(temp, column);if(value > maxValue){maxValue = value;r1 = i;c1 = ans_start;r2 = j;c2 = ans_end;}}}Ans[0] = r1;Ans[1] = c1;Ans[2] = r2;Ans[3] = c2;return Ans;}
};题目七
测试链接:https://leetcode.cn/problems/maximum-product-subarray/
分析:因为数组中的值有正有负,所以对于dp数组需要求得以下标i为结尾的最大值和最小值。下面直接给出空间压缩的版本。代码如下。
class Solution {
public:int maxProduct(vector<int>& nums) {int last_max, last_min, cur_max, cur_min;int length = nums.size();int ans = nums[0];last_min = nums[0];last_max = nums[0];for(int i = 1;i < length;++i){if(nums[i] == 0){cur_max = 0;cur_min = 0;}else{if(nums[i] < 0){cur_max = last_min < 0 ? last_min * nums[i] : nums[i];cur_min = last_max > 0 ? last_max * nums[i] : nums[i];}else{cur_max = last_max > 0 ? last_max * nums[i] : nums[i];cur_min = last_min < 0 ? last_min * nums[i] : nums[i];}}ans = ans > cur_max ? ans : cur_max;last_max = cur_max;last_min = cur_min;}return ans;}
};题目八
子序列累加和必须被7整除的最大累加和
给定一个非负数组nums,
可以任意选择数字组成子序列,但是子序列的累加和必须被7整除
返回最大累加和
分析:dp[i][j]代表以前i个数除以7余数为j的最大累加和。代码如下。
class Solution {
public:int dp[10000][7] = {0};int get_max(vector<int>& nums) {int length = nums.size();int cur;for(int i = 1;i <= length;++i){cur = nums[i-1] % 7;for(int j = 0;j < 7;++j){dp[i][j] = dp[i-1][j];if(cur <= j){dp[i][j] = dp[i][j] > dp[i-1][j-cur] + nums[i-1] ? dp[i][j] : dp[i-1][j-cur] + nums[i-1];}else{dp[i][j] = dp[i][j] > dp[i-1][j-cur+7] + nums[i-1] ? dp[i][j] : dp[i-1][j-cur+7] + nums[i-1];}}}return dp[length][0];}
};题目九
魔法卷轴
给定一个数组nums,其中可能有正、负、0
每个魔法卷轴可以把nums中连续的一段全变成0
你希望数组整体的累加和尽可能大
卷轴使不使用、使用多少随意,但一共只有2个魔法卷轴
请返回数组尽可能大的累加和
分析:这道题可以将情况拆开来看,对于不使用、使用1次、使用2次分别求出数组累加和,相比较即可得出最大值。不使用时就是简单的求和,使用1次可以看成是求出数组中子数组最小累加和,如果大于等于0,代表数组全部为非负数,故直接返回数组累加和即可;如果最小累加和等于数组累加和,代表数组全是负数,故直接返回0即可。使用2次就需要在找到一个次小累加和,因为次小累加和和最小累加和的范围一定是不重合的,所以对于次小累加和的寻找可以看成是在最小累加和范围之外的左右两边数组中寻找最小累加和,取最小的即可得到次小累加和,如果次小累加和大于等于0,代表只需要使用1次;否则需要使用2次。代码如下。
class Solution {
public:int get_max(vector<int>& nums) {int all = 0;int last, last_start, cur, cur_start;int min_value, min_start, min_end;int length = nums.size();for(int i = 0;i < length;++i){all += nums[i];}min_value = nums[0];last = nums[0];last_start = 0;min_start = 0;min_end = 0;for(int i = 1;i < length;++i){cur = last >= 0 ? last : last + nums[i];cur_start = last >= 0 ? i : last_start;if(cur < min_value){min_value = cur;min_start = cur_start;min_end = i;}last = cur;last_start = cur_start;}if(min_value >= 0){return all;}if(min_value == all){return 0;}int minest = min_value;int start = 0, end = min_start-1, temp1 = 0, temp2 = 0;if(start <= end){min_value = nums[start];last = nums[start];for(int i = start;i <= end;++i){cur = last >= 0 ? nums[i] : last + nums[i];min_value = min_value < cur ? min_value : cur;}temp1 = min_value;}start = min_end+1;end = length-1;if(start <= end){min_value = nums[start];last = nums[start];for(int i = start;i <= end;++i){cur = last >= 0 ? nums[i] : last + nums[i];min_value = min_value < cur ? min_value : cur;}temp2 = min_value;}int tmp = temp1 < temp2 ? temp1 : temp2;if(tmp >= 0){return all - minest;}return all - minest - tmp;}
};题目十
测试链接:https://leetcode.cn/problems/maximum-sum-of-3-non-overlapping-subarrays/
分析:这道题思路是构造前缀后缀信息,在数组中截取一个长度为k的子数组,然后用前缀信息和后缀信息求得3个子数组的和,遍历数组即可求得最大值。prefix[i]代表以下标i结尾时长度为k的最大累加和子数组的开始下标,suffix[i]代表以下标i为开头时长度为k的最大累加和子数组的开始下标。代码如下。
class Solution {
public:int Sum[20001];int prefix[20001];int suffix[20001];vector<int> maxSumOfThreeSubarrays(vector<int>& nums, int k) {int length = nums.size();int window = 0;int ans = 0;vector<int> Ans;Ans.assign(3, 0);int index1, index2, index3;for(int i = 0;i < k;++i){window += nums[i];}Sum[0] = window;for(int i = 1;i < length-k+1;++i){window -= nums[i-1];window += nums[i+k-1];Sum[i] = window;}prefix[k-1] = 0;for(int i = k;i < length-k+1;++i){prefix[i] = Sum[prefix[i-1]] >= Sum[i-k+1] ? prefix[i-1] : i-k+1;}suffix[length-k] = length-k;for(int i = length-k-1;i >= 0;--i){suffix[i] = Sum[suffix[i+1]] > Sum[i] ? suffix[i+1] : i;}for(int i = k;i < length-2*k+1;++i){if(ans < Sum[i] + Sum[prefix[i-1]] + Sum[suffix[i+k]]){ans = Sum[i] + Sum[prefix[i-1]] + Sum[suffix[i+k]];index1 = prefix[i-1];index2 = i;index3 = suffix[i+k];}}Ans[0] = index1;Ans[1] = index2;Ans[2] = index3;return Ans;}
};题目十一
可以翻转1次的情况下子数组最大累加和
给定一个数组nums,
现在允许你随意选择数组连续一段进行翻转,也就是子数组逆序的调整
比如翻转[1,2,3,4,5,6]的[2~4]范围,得到的是[1,2,5,4,3,6]
返回必须随意翻转1次之后,子数组的最大累加和
分析:可以看出,翻转其实是选定一个边界,边界左边的进行翻转,边界右边的不动,或者左边不动右边翻转。这样只需要得到边界左边以边界为结尾的子数组最大累加和以及边界右边以边界为开头的子数组最大累加和,相加即是这个边界的答案。遍历数组即可得到子数组的最大累加和。代码如下。
class Solution {
public:int get_reverse_max(vector<int>& nums) {int dp1[10000] = {0};int dp2[10000] = {0};int ans;int length = nums.size();dp1[0] = nums[0];for(int i = 1;i < length;++i){dp1[i] = dp1[i-1] > 0 ? dp1[i-1] + nums[i] : nums[i];}dp2[length-1] = nums[length-1];for(int i = length-2;i >= 0;--i){dp2[i] = dp2[i+1] > 0 ? dp2[i+1] + nums[i] : nums[i];}ans = dp2[0];int front_max = dp1[0];for(int i = 1;i < length;++i){front_max = front_max > dp1[i-1] ? front_max : dp1[i-1];ans = ans > front_max + dp2[i] ? ans : front_max + dp2[i];}return ans;}
};题目十二
删掉1个数字后长度为k的子数组最大累加和
给定一个数组nums,求必须删除一个数字后的新数组中
长度为k的子数组最大累加和,删除哪个数字随意
分析:这道题可以理解为,对于每一个长度为k+1的子数组,删除这这个子数组中的最小值,从每一个长度为k+1的子数组中求得结果。因为子数组要减去子数组范围内的最小值,所以可以采用单调队列。代码如下。
class Solution {
public:int get_delete1_max(vector<int>& nums, int k) {int length = nums.size();if(length <= k){return 0;}vector<int> window;window.assign(length, 0);int l = 0;int r = 0;long sum = 0;int ans = (1 << 31);for(int i = 0;i < length;++i){while (l < r && nums[window[r-1]] >= nums[i]){--r;}window[r++] = i;sum += nums[i];if(i >= k){ans = ans > sum - nums[window[l]] ? ans : sum - nums[window[l]];if(window[l] == i-k){++l;}sum -= nums[i-k];}}return ans;}
};相关文章:

算法【子数组最大累加和问题与扩展】
子数组最大累加和问题是一个非常经典的问题,也比较简单。但是扩展出的问题很多,在笔试、面试中特别常见,扩展出的问题很多非常有趣,解法也比较巧妙。 下面通过一些题目来加深理解。 题目一 测试链接:https://leetcode…...

小程序23-页面的跳转:navigation 组件详解
小程序中,如果需要进行跳转,需要使用 navigation 组件,常用属性: 1.url :当前小程序内的跳转链接 2.open-type:跳转方式 navigate:保留当前页面,跳转应用内的某个页面,…...

AI社媒引流工具:解锁智能化营销的新未来
在数字化浪潮的推动下,社交媒体成为品牌营销的主战场。然而,面对海量的用户数据和日益复杂的运营需求,传统营销方法显得力不从心。AI社媒引流王应运而生,帮助企业在多平台中精准触达目标用户,提升营销效率和效果。 1.…...

【Node.js】全面解析 Node.js 安全最佳实践:保护您的应用
Node.js 是一种强大的 JavaScript 运行时,广泛用于构建现代 Web 应用和 API。然而,由于其开放性和异步特性,Node.js 应用容易受到多种安全威胁的攻击,比如 SQL 注入、跨站脚本 (XSS) 和拒绝服务攻击 (DoS)。在本文中,我…...

Docker 用法详解
文章目录 一、Docker 快速入门1.1 部署 MYSQL1.2 命令解读: 二、Docker 基础2.1 常见命令:2.1.1 命令介绍:2.1.2 演示:2.1.3 命令别名: 2.2 数据卷:2.2.1 数据卷简介:2.2.2 数据卷命令ÿ…...
Python小游戏28——水果忍者
首先,你需要安装Pygame库。如果你还没有安装,可以使用以下命令进行安装: 【bash】 pip install pygame 《水果忍者》游戏代码: 【python】 import pygame import random import sys # 初始化Pygame pygame.init() # 设置屏幕尺寸 …...

Kafka Offset 自动提交和手动提交 - 漏消费与重复消费
目录 1. 引言 2. Offset 提交方式概述 2.1 自动提交 Offset 2.2 手动提交 Offset 3. 漏消费与重复消费的问题分析 3.1 自动提交模式下的漏消费和重复消费 漏消费 重复消费 3.2 手动提交模式下的漏消费和重复消费 漏消费 重复消费 4. 自动提交与手动提交的选择 4.1…...

Vue3父组件和子组件
子组件暴露方法给父组件,父组件传值 子组件 const editCalendar (value: string) > {console.log(获取父组件的值, value)};//暴露给外部调用defineExpose({editCalendar,}); 父组件 <template> <CalendarEdit ref"editRef" /> </…...

Linux 定时任务全解析
文章目录 一、Cron 服务1.1安装1.2配置文件格式1.3使用方法1.4系统级与用户级 Cron 任务区别 二、At 服务2.1安装2.2工作原理2.3使用方法 一、Cron 服务 1.1安装 在大多数 Linux 发行版中,Cron 服务通常已经默认安装。例如在 Ubuntu 系统中,可以通过以…...

XLNet——打破 BERT 局限的预训练语言模型
近年来,深度学习在自然语言处理(NLP)领域取得了革命性进展,其中 BERT 的出现标志着双向语言建模的强大能力。然而,BERT 也存在一些局限性,限制了其在生成任务中的表现。2019 年,由 Google 和 Ca…...
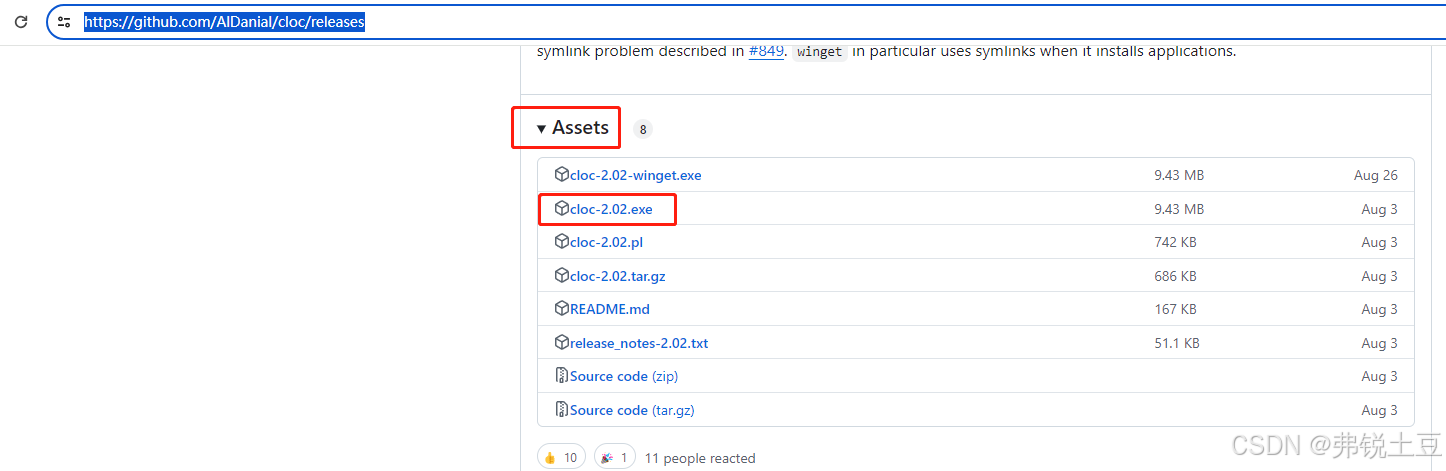
开源代码统计工具cloc的简单使用
一.背景 公司之前开发了个小系统,要去申请著作权,需要填写代码数量。应该怎么统计呢?搜索了一下,还是用开源工具cloc吧!我的操作系统是windows,代码主要是java项目和vue项目。 二.到哪里找 可以去官方下载…...

如何创建一个项目用于研究element-plus的原理
需求:直接使用element-plus未封装成组件的源码,创建一个项目,可以使用任意的element-plus组件,可以深度研究组件的运行。例如研究某一个效果,如果直接在node_modules修改elment-plus打包之后的那些js、mjs代码…...
单片机进阶硬件部分_day2_项目实践
设计要求 从绘制原理图到画PCB板,完成智能云衣柜项目 STM32 (Modbus)云IOT衣物云端管理 华为PCB布线规范 基于IoT的智享家主控系统 步骤分析 需求分析 器件选型绘制原理图(器件连接)PCB布局、布线泪滴、铺铜、添加丝印…...
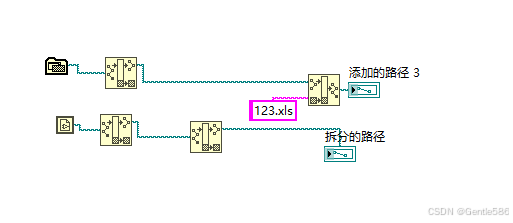
labview关于文件路径的问题
在调用文件或拆分文件的时候经常会用到拆分路径函数和创建路径函数,最常用的也是当前应用程序目录或者是当前VI目录。 这里我们看到应用程序目录和VI目录在同一项目中,应用程序目录更像是根目录,往下拆分成了各个VI的子目录。 接下来我们来拆…...
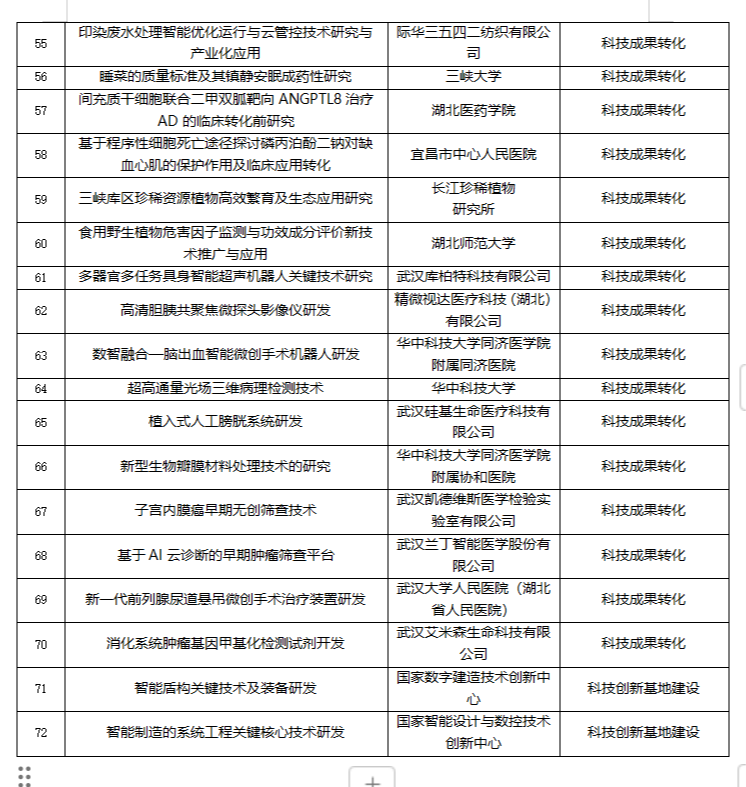
72项!湖北省2024年度第二批省级科技计划项目拟立项项目公示!
本期精选 SCI&EI ●IEEE 1区TOP 计算机类(含CCF); ●EI快刊:最快1周录用! 知网(CNKI)、谷歌学术期刊 ●7天录用-检索(100%录用),1周上线; 免费稿件评估 免费匹配…...
神经网络问题之:梯度不稳定
梯度不稳定是深度学习中,特别是在训练深度神经网络时常见的一个问题,其本质涉及多个方面。 一、根本原因 梯度不稳定问题的根本原因在于深度神经网络的结构和训练过程中的一些固有特性。随着网络层数的增加,梯度在反向传播过程中会逐层累积变…...

ORACLE删不掉job,如何解决。
问题: 删掉 NYZSM 时出错: ORA-27478: 作业 “ZHY.NYZSM” 正在运行 ORA-06512: 在 “SYS.DBMS_ISCHED”, line 213 ORA-06512: 在 “SYS.DBMS_SCHEDULER”, line 657 ORA-06512: 在 line 2 1、停止作业: 使用DBMS_SCHEDULER.STOP_JOB过程来…...
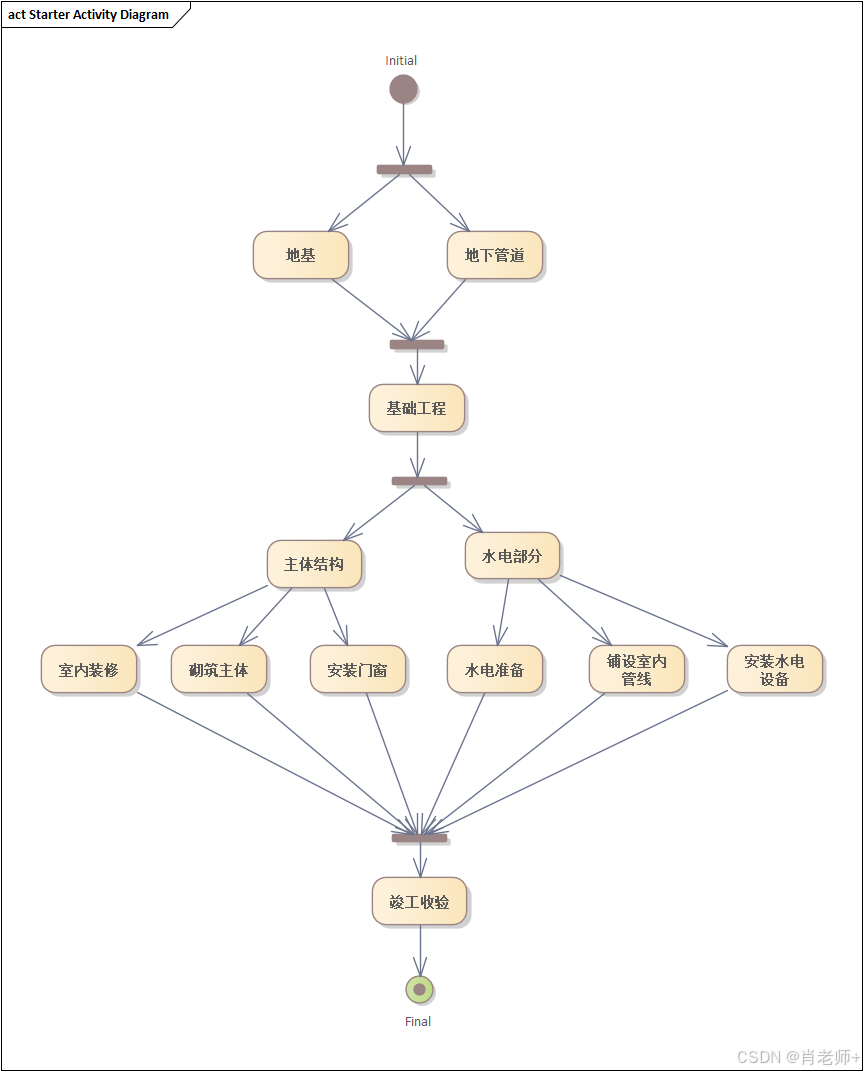
可视化建模与UML《活动图实验报告》
你当像鸟飞往你的山。 一、实验目的: 1、熟悉活动图的基本功能和使用方法。 2、掌握使用建模工具软件绘制协作图的方法 二、实验环境: window7 | 10 | 11 EA15 三、实验内容: <1>绘制学生选课系统中添加课程(Add Course)用例的活动图…...

基于 MUSA 的大语言模型推理和服务框架vLLM
1. 引言 vLLM是一个高性能且内存高效的大语言模型推理和服务框架,也是当前业界使用范围最广的大模型推理框架,截至目前github star数28.4k。该框架性能优秀,而且部署容易,使用CUDA/ROCm提供GPU加速能力。但vLLM目前不支持使用摩…...
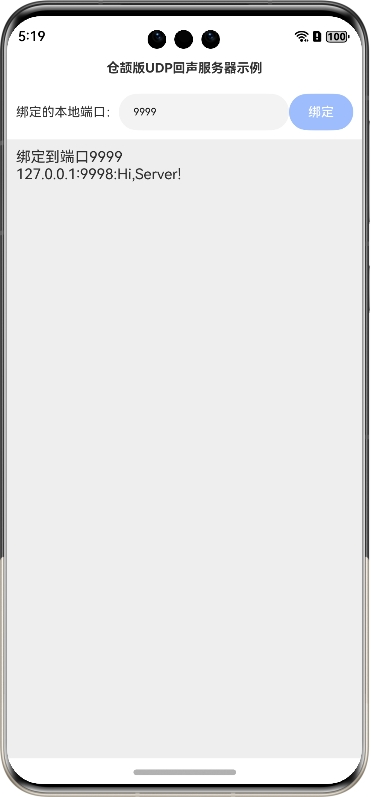
鸿蒙网络编程系列48-仓颉版UDP回声服务器示例
1. UDP回声服务器简介 回声服务器指的是这样一种服务器,它接受客户端的连接,并且把收到的数据原样返回给客户端,本系列的第2篇文章《鸿蒙网络编程系列2-UDP回声服务器的实现》中基于ArkTS语言在API 9的环境下实现了UDP回声服务器,…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...
