【机器学习】聚类算法原理详解
聚类算法
性能度量:
- 外部指标
jaccard系数(简称JC)FM指数(简称FMI)Rand指数(简称RI)
- 内部指标
DB指数(简称DBI)Dunn指数(简称DI)
距离计算:
- L p L_p Lp 范数
- 欧氏距离
- 曼哈顿距离
分类:
- 原型聚类:
k-means算法,学习向量量化(有监督学习),高斯混合聚类 都是此类型算法
假设聚类结构能够通过一组原型刻画,然后对原型进行迭代更新求解。
-
密度聚类:DBSCAN
-
层次聚类:AGNES
试图在不同层次上对数据集进行划分,分为自底向上的聚合策略和自顶向下的分拆策略
聚簇之间的距离的计算:最小距离,最大距离和平均距离(两个簇中样本点对距离之和取平均)
AGNES算法被相应称为:单链接算法(以最小距离为准),全链接算法(以最大距离为准)和均链接算法
以单链接算法为例:
- 初始时每个样本点看做一个簇,找到所有簇对中最小的距离,将他们合并为一个簇,此时合并的簇与其他簇的距离更新为两个点到其他簇距离的最小值。
- 上面的步骤为循环里面的步骤,接着进行下一次循环,找到所有簇中最短的距离,然后将他们合并,合并后更新簇之间的距离为【合并簇中的所有点到其他簇距离的最小值】,一直进行上述循环操作,直到达到指定簇的数量再停止循环。
K-MEANS算法
1 概述
聚类概念:这是个无监督问题(没有标签数据),目的是将相似的东西分到一组。
通常使用的算法是K-MEANS算法
K-MEANS算法:
- 需要指定簇的个数,即K值
- 质心:数据的均值,即向量各维取平均即可
- 距离的度量:常用欧几里得距离和余弦相似度(先标准化,让数据基本都是在一个比较小的范围内浮动)
- 优化目标: m i n ∑ i = 1 K ∑ x ∈ C i d i s t ( c i , x ) 2 min\sum \limits_{i = 1}^K \sum \limits_{x \in C_i} dist(c_i, x)^2 mini=1∑Kx∈Ci∑dist(ci,x)2 (对于每一个簇让每一个样本到中心点的距离越小越好, c i c_i ci代表中心点)
2 K-MEANS流程
假设平面上有一系列样本点,现在需要将其进行分组。
选定K=2,即将这些数据点分成两个组别。
- 随机选择两个质心(分别代表两个簇),计算所有样本点到两个质心的距离。每个样本点会计算出到两个质心的距离,那么选择最小的距离,这个样本点就归属于哪个簇。
- 然后对于两个簇的所有样本点分别算出对应的质心(这两个质心便充当新的质心),再对所有样本点计算到两个新的质心的距离,还是选择最小的距离,那么这个样本点就归属于哪个簇。
- 最终直到两个簇所属的样本点不在发生变化。
K-MEANS工作流程视频参考
3 优缺点
优点:
- 简单快速,适合常规数据集
缺点:
- K值难以确定
- 复杂度与样本呈线性关系
- 很难发现任意形状的簇
- 初始的点影响很大
K-MEANS可视化演示
4 K-MEANS进行图像压缩
from skimage import io
from sklearn.cluster import KMeans
import numpy as npimage = io.imread("1.jpg")
io.imshow(image)
# io.show() # 显示图片rows = image.shape[0]
cols = image.shape[1]
print(image.shape)image = image.reshape(rows * cols, 3)
kmeans = KMeans(n_clusters=128, n_init=10, max_iter=100) # 簇128, 最大迭代次数100
kmeans.fit(image)clusters = np.asarray(kmeans.cluster_centers_, dtype=np.uint8)
labels = np.asarray(kmeans.labels_, dtype=np.uint8)
labels = labels.reshape(rows, cols)print(clusters.shape)
np.save('test.npy', clusters)
io.imsave('compressed.jpg', labels)
DBSCAN算法
1 概述
DBSCAN(Density-Based Spatial Clustering of Applications with Noise,具有噪声的基于密度的聚类方法)是一种基于密度的空间聚类算法。该算法将具有足够密度的区域划分为簇,并在具有噪声的空间数据库中发现任意形状的簇,DBSCAN算法将簇定义为密度相连的点的最大集合。
核心对象:若某个点的密度达到算法设定的阈值则称其为核心点。(即r邻域内的点的数量不小于minPts)
基于以上密度的定义,我们可以将样本集中的点划分为以下三类:
- 核心点:在半径r区域内,含有超过MinPts数目(最小数目)的点,称为核心点;
- 边界点:在半径r区域内,点的数量小于MinPts数目,但是是核心点的直接邻居;
- 噪声点:既不是核心点也不是边界点的点
噪声点是不会被聚类纳入的点,边界点与核心点组成聚类的“簇”。
一些概念:
- 直接密度可达(密度直达):如果p在q的r领域内,且q是一个核心点对象,则称对象p从对象q出发时直接密度可达,反之不一定成立,即密度直达不满足对称性。
- 密度可达:如果存在一个对象链q–>e–>a–>k–>l–>p,任意相邻两个对象间都是密度直达的,则称对象p由对象q出发密度可达。密度可达满足传递性。
- 密度相连:对于 x i x_i xi 和 x j x_j xj ,如果存在核心对象样本 x k x_k xk ,使 x i x_i xi 和 x j x_j xj 均由 x k x_k xk 密度可达,则称 x i x_i xi 和 x j x_j xj 密度相连。密度相连关系满足对称性。
核心点能够连通(密度可达),它们构成的以r为半径的圆形邻域相互连接或重叠,这些连通的核心点及其所处的邻域内的全部点构成一个簇。
2 原理
- DBSCAN通过检查数据集中每个点的r邻域来搜索簇,如果点p的r邻域包含多于MinPts个点,则创建一个以p为核心对象的簇;
- 然后, DBSCAN迭代的聚集从这些核心对象直接密度可达的对象,这个过程可能涉及一些密度可达簇的合并;
- 当没有新的带你添加到任何簇时,迭代过程结束。
优缺点:
-
优点:基于密度定义,可以对抗噪声,能处理任意形状和大小的簇
-
缺点:当簇的密度变化太大时候,聚类得到的结果会不理想;对于高维问题,密度定义也是一个比较麻烦的问题。
3 实现
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
import matplotlib.colors# 创建Figure
fig = plt.figure()
# 用来正常显示中文标签
matplotlib.rcParams['font.sans-serif'] = [u'SimHei']
# 用来正常显示负号
matplotlib.rcParams['axes.unicode_minus'] = FalseX1, y1 = datasets.make_circles(n_samples=5000, factor=.6,noise=.05)
X2, y2 = datasets.make_blobs(n_samples=1000, n_features=2,centers=[[1.2,1.2]], cluster_std=[[.1]],random_state=9)# 原始点的分布
ax1 = fig.add_subplot(311)
X = np.concatenate((X1, X2))
plt.scatter(X[:, 0], X[:, 1], marker='o')
plt.title(u'原始数据分布')
plt.sca(ax1)# K-means聚类
from sklearn.cluster import KMeans
ax2 = fig.add_subplot(312)
y_pred = KMeans(n_clusters=3, random_state=9).fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.title(u'K-means聚类')
plt.sca(ax2)# DBSCAN聚类
from sklearn.cluster import DBSCAN
ax3 = fig.add_subplot(313)
y_pred = DBSCAN(eps = 0.1, min_samples = 10).fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.title(u'DBSCAN聚类')
plt.sca(ax3)plt.show()
相关文章:

【机器学习】聚类算法原理详解
聚类算法 性能度量: 外部指标 jaccard系数(简称JC)FM指数(简称FMI)Rand指数(简称RI) 内部指标 DB指数(简称DBI)Dunn指数(简称DI) 距离计算&am…...
Ubuntu20.04从零安装IsaacSim/IsaacLab
Ubuntu20.04从零安装IsaacSim/IsaacLab 电脑硬件配置:安装Isaac sim方案一:pip安装方案二:预构建二进制文件安装1、安装ominiverse2、在ominiverse中安装isaac sim,下载最新的4.2版本 安装Isaac Lab1、IsaacLab环境克隆2、创建con…...

基于Java Springboot大学校园旧物捐赠网站
一、作品包含 源码数据库设计文档万字PPT全套环境和工具资源部署教程 二、项目技术 前端技术:Html、Css、Js、Vue、Element-ui 数据库:MySQL 后端技术:Java、Spring Boot、MyBatis 三、运行环境 开发工具:IDEA/eclipse 数据…...

【Java 集合】Collections 空列表细节处理
问题 如下代码,虽然定义为非空 NonNull,但依然会返回空对象,导致调用侧被检测为空引用。 实际上不是Collections的问题是三目运算符返回了null对象。 import java.util.Collections;NonNullprivate List<String> getInfo() {IccReco…...
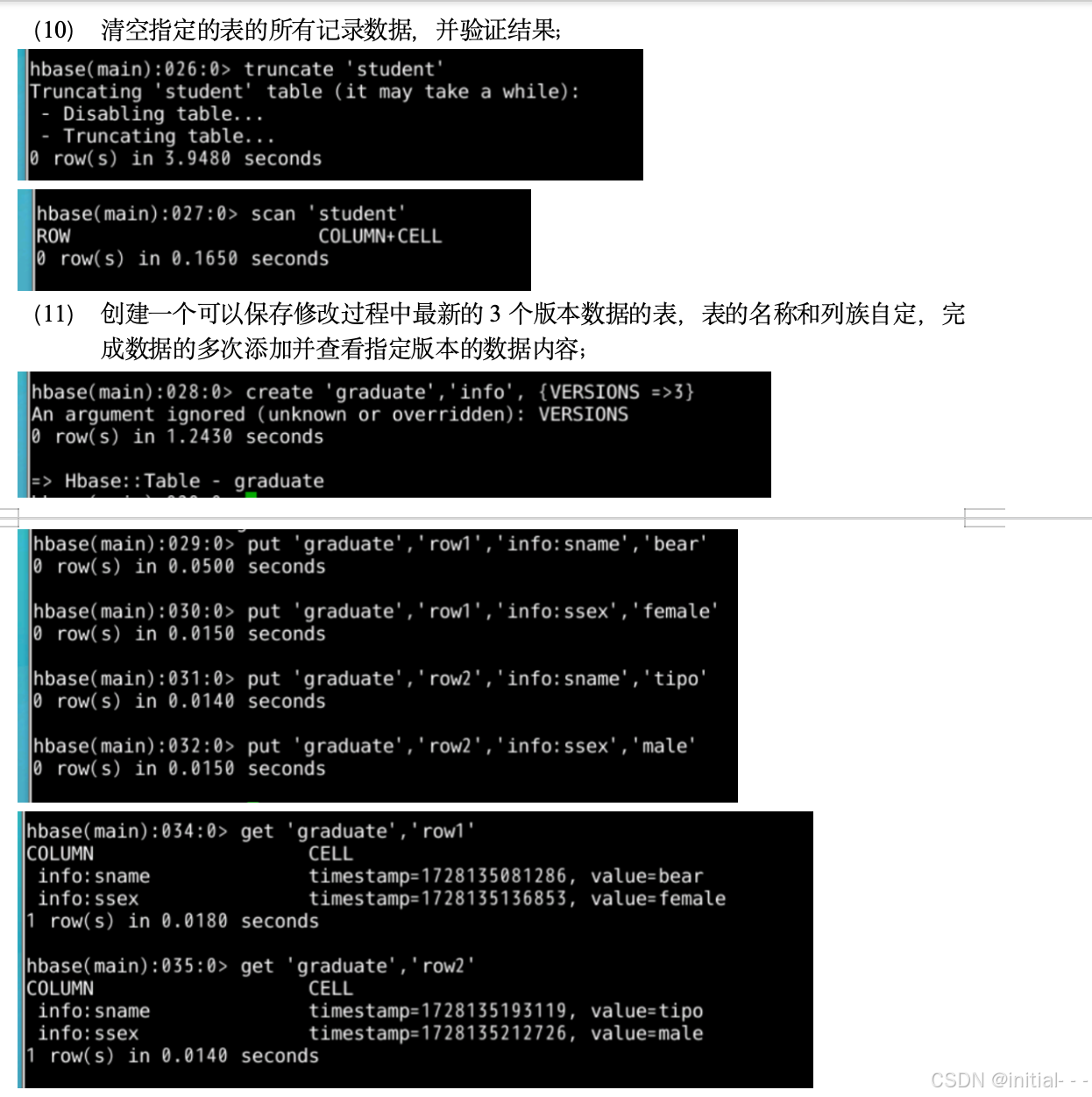
大数据实验4-HBase
一、实验目的 阐述HBase在Hadoop体系结构中的角色;能够掌握HBase的安装和配置方法熟练使用HBase操作常用的Shell命令; 二、实验要求 学习HBase的安装步骤,并掌握HBase的基本操作命令的使用; 三、实验平台 操作系统࿱…...

deepin系统下载pnpm cnpm等报错
deepin系统下载pnpm cnpm等报错 npm ERR! request to https://registry.npm.taobao.org/pnpm failed, reason: certificate has expired 报错提示证书过期,执行以下命令 npm config set registry https://registry.npmmirror.com下载pnpm npm install pnpm -g查…...

#Js篇:JSON.stringify 和 JSON.parse用法和传参
JSON.stringify 和 JSON.parse 1. JSON.stringify JSON.stringify 方法将一个 JavaScript 对象或数组转换为 JSON 字符串。 基本用法 const obj { name: "Alice", age: 25 }; const jsonString JSON.stringify(obj); console.log(jsonString); // 输出: {"…...

c#通过网上AI大模型实现对话功能
目录 基础使用给大模型额外提供函数能力用Microsoft.Extensions.AI库实现用json格式回答 基础使用 https://siliconflow.cn/网站有些免费的大模型可以使用,去注册个账户,拿到apikey 引用 nuget Microsoft.Extensions.AI.OpenAI using Microsoft.Extensi…...
pymysql模块
1.pymysql基本使用 打开数据库连接,使用cursor()方法获取操作游标执行SQL语句 获取命令执行的查询结果 1.1 打开数据库连接 # 打开数据库连接 db pymysql.connect(host127.0.0.1,userroot,port3306,password"123",databasedb5) 1.2 使用cursor()方法获取操作游…...
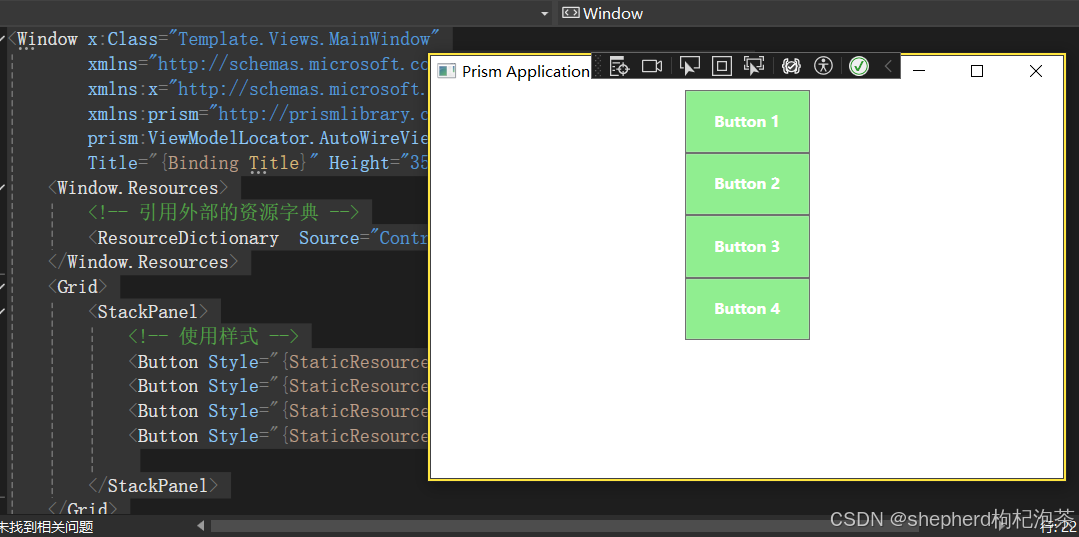
WPF-模板和样式
在 WPF(Windows Presentation Foundation)中,模板是一种强大的机制,用于定义控件的外观。它允许你将控件的逻辑(功能)和外观(UI)分离开来。例如,一个按钮控件,…...
网络编程 day1.2~day2——TCP和UDP的通信基础(TCP)
笔记脑图 作业: 1、将虚拟机调整到桥接模式联网。 2、TCP客户端服务器实现一遍。 服务器 #include <stdio.h> #include <string.h> #include <myhead.h> #define IP "192.168.60.44" #define PORT 6666 #define BACKLOG 20 int mai…...

element ui table 每行不同状态
table 每行定义值 tableData: [ { name: ,type:,location:, ziduan:,createtype:,ziduanvalue:,checkAll:true,checkedCities: [空, null, str随机, int随机],isIndeterminate: true,table_id:single,downloaddisabled:true,deldisabled:true} ], table c…...

力扣--LRC 142.训练计划IV
题目 给定两个以 有序链表 形式记录的训练计划 l1、l2,分别记录了两套核心肌群训练项目编号,请合并这两个训练计划,按训练项目编号 升序 记录于链表并返回。 注意:新链表是通过拼接给定的两个链表的所有节点组成的。 示例 1&am…...
windows下,用CMake编译qt项目,出现错误By not providing “FindQt5.cmake“...
开发环境:windows10 qt5.14, 编译器msvc2017x64,CMake3.30; 现象: CMakeList文件里,如有find_package(Qt5 COMPONENTS Widgets REQUIRED) target_link_libraries(dis_lib PRIVATE Qt5::Widgets) 用CMak…...

【element-tiptap】Tiptap编辑器核心概念----结构篇
core-concepts 前言:这篇文章来介绍一下 Tiptap 编辑器的一些核心概念 (一)结构 1、 Schemas 定义文档组成方式。一个文档就是标题、段落以及其他的节点组成的一棵树。 每一个 ProseMirror 的文档都有一个与之相关联的 schema,…...

半导体工艺与制造篇3 离子注入
离子注入工艺 一般掺杂的杂质类别,包括:提供载流子的施主杂质和受主杂质;产生复合中心的重金属杂质 离子注入往往需要生成井well,其中井的定义:晶圆与杂质之间形成的扩散层或杂质与杂质之间形成的扩散层 离子注入的目的:用掺杂改…...
利用开源的低代码表单设计器FcDesigner高效管理和渲染复杂表单结构
FcDesigner 是一个强大的开源低代码表单设计器组件,支持快速拖拽生成表单。提供丰富的自定义及扩展功能,FcDesigner支持多语言环境,并允许开发者进行二次开发。通过将表单设计输出为JSON格式,再通过渲染器进行加载,实现…...

淘宝 NPM 镜像源
npm i vant/weapp -S --production npm config set registry https://registry.npmmirror.com 要在淘宝 NPM 镜像站下载项目或依赖,你可以按照以下步骤操作: 1. 设置淘宝 NPM 镜像源 首先,你需要设置淘宝 NPM 镜像源以加速下载。可以通过…...
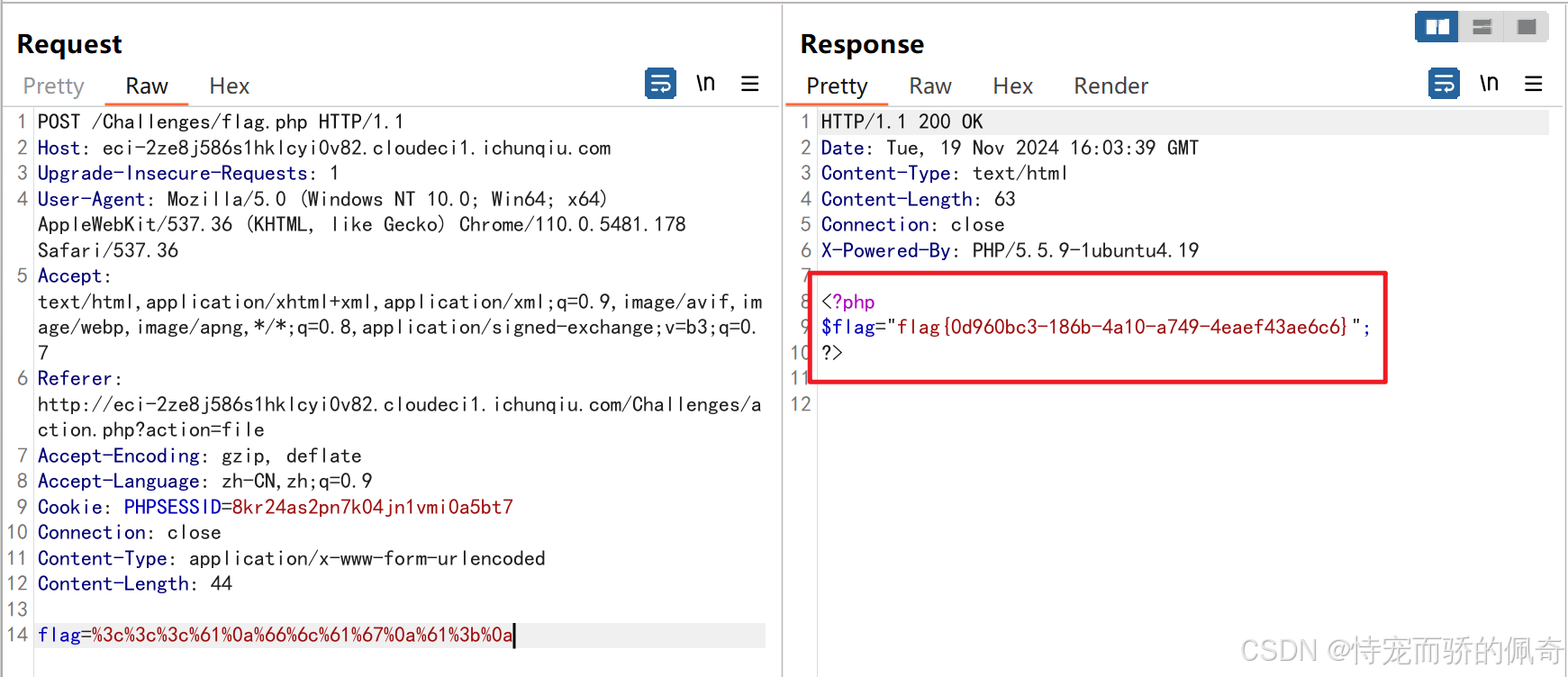
i春秋-GetFlag(md5加密,字符串比较绕过)
练习平台地址 竞赛中心 题目描述 题目内容 你好,单身狗,这是一个迷你文件管理器,你可以登录和下载文件,甚至得到旗帜 点击登录 发现capture需要满足条件substr(md5(captcha), 0, 6)xxxxxx 编写python脚本破解验证码 import has…...
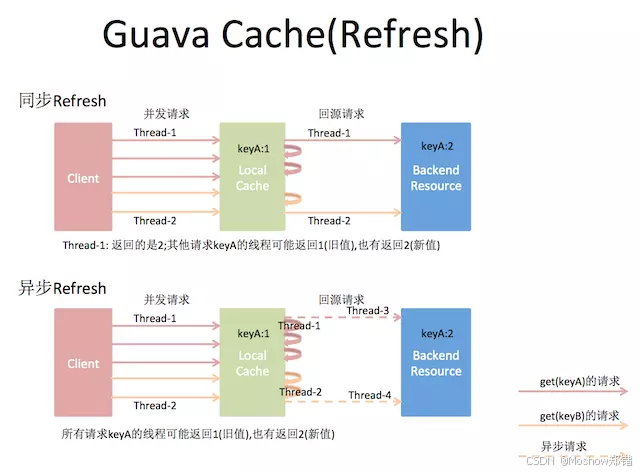
SpringBoot中设置超时30分钟自动删除元素的List和Map
简介 在 Spring Boot 中,你可以使用多种方法来实现自动删除超时元素的 List 或 Map。以下是两种常见的方式: 如果你需要简单的功能并且不介意引入外部依赖,可以选择 Guava Cache。如果你想要更灵活的控制,使用 Spring 的调度功能…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...
