【题解】—— LeetCode一周小结46
🌟欢迎来到 我的博客 —— 探索技术的无限可能!
🌟博客的简介(文章目录)
【题解】—— 每日一道题目栏
上接:【题解】—— LeetCode一周小结45

11.切棍子的最小成本
题目链接:1547. 切棍子的最小成本
有一根长度为 n 个单位的木棍,棍上从 0 到 n 标记了若干位置。例如,长度为 6 的棍子可以标记如下:

给你一个整数数组 cuts ,其中 cuts[i] 表示你需要将棍子切开的位置。
你可以按顺序完成切割,也可以根据需要更改切割的顺序。
每次切割的成本都是当前要切割的棍子的长度,切棍子的总成本是历次切割成本的总和。对棍子进行切割将会把一根木棍分成两根较小的木棍(这两根木棍的长度和就是切割前木棍的长度)。请参阅第一个示例以获得更直观的解释。
返回切棍子的 最小总成本 。
示例 1:
输入:n = 7, cuts = [1,3,4,5]
输出:16
解释:按 [1, 3, 4, 5] 的顺序切割的情况如下所示:
第一次切割长度为 7 的棍子,成本为 7 。第二次切割长度为 6 的棍子(即第一次切割得到的第二根棍子),第三次切割为长度 4
的棍子,最后切割长度为 3 的棍子。总成本为 7 + 6 + 4 + 3 = 20 。 而将切割顺序重新排列为 [3, 5, 1, 4]
后,总成本 = 16(如示例图中 7 + 4 + 3 + 2 = 16)。
示例 2:
输入:n = 9, cuts = [5,6,1,4,2]
输出:22
解释:如果按给定的顺序切割,则总成本为 25 。总成本 <= 25 的切割顺序很多,例如,[4, 6, 5, 2, 1] 的总成本 =
22,是所有可能方案中成本最小的。
提示:
2 <= n <= 10^6
1 <= cuts.length <= min(n - 1, 100)
1 <= cuts[i] <= n - 1
cuts 数组中的所有整数都 互不相同
题解:
方法:记忆化搜索
class Solution {public int minCost(int n, int[] cuts) {Arrays.sort(cuts);int m = cuts.length + 2;int[] newCuts = new int[m];System.arraycopy(cuts, 0, newCuts, 1, m - 2);newCuts[m - 1] = n;int[][] memo = new int[m][m];return dfs(0, m - 1, newCuts, memo);}private int dfs(int i, int j, int[] cuts, int[][] memo) {if (i + 1 == j) { // 无需切割return 0;}if (memo[i][j] > 0) { // 之前计算过return memo[i][j];}int res = Integer.MAX_VALUE;for (int k = i + 1; k < j; k++) {res = Math.min(res, dfs(i, k, cuts, memo) + dfs(k, j, cuts, memo));}return memo[i][j] = res + cuts[j] - cuts[i];}
}
12.统计满足 K 约束的子字符串数量 I
题目链接:3258. 统计满足 K 约束的子字符串数量 I
给你一个 二进制 字符串 s 和一个整数 k。
如果一个 二进制字符串 满足以下任一条件,则认为该字符串满足 k 约束:
字符串中 0 的数量最多为 k。
字符串中 1 的数量最多为 k。
返回一个整数,表示 s 的所有满足 k 约束 的
子字符串
的数量。
示例 1:
输入:s = “10101”, k = 1
输出:12
解释:
s 的所有子字符串中,除了 “1010”、“10101” 和 “0101” 外,其余子字符串都满足 k 约束。
示例 2:
输入:s = “1010101”, k = 2
输出:25
解释:
s 的所有子字符串中,除了长度大于 5 的子字符串外,其余子字符串都满足 k 约束。
示例 3:
输入:s = “11111”, k = 1
输出:15
解释:
s 的所有子字符串都满足 k 约束。
提示:
1 <= s.length <= 50
1 <= k <= s.length
s[i] 是 ‘0’ 或 ‘1’。
题解:
方法:滑动窗口
class Solution {public int countKConstraintSubstrings(String S, int k) {char[] s = S.toCharArray();int ans = 0;int left = 0;int[] cnt = new int[2];for (int i = 0; i < s.length; i++) {cnt[s[i] & 1]++;while (cnt[0] > k && cnt[1] > k) {cnt[s[left] & 1]--;left++;}ans += i - left + 1;}return ans;}
}
13.统计满足 K 约束的子字符串数量 II
题目链接:3261. 统计满足 K 约束的子字符串数量 II
给你一个 二进制 字符串 s 和一个整数 k。
另给你一个二维整数数组 queries ,其中 queries[i] = [li, ri] 。
如果一个 二进制字符串 满足以下任一条件,则认为该字符串满足 k 约束:
字符串中 0 的数量最多为 k。
字符串中 1 的数量最多为 k。
返回一个整数数组 answer ,其中 answer[i] 表示 s[li…ri] 中满足 k 约束 的
子字符串
的数量。
示例 1:
输入:s = “0001111”, k = 2, queries = [[0,6]]
输出:[26]
解释:
对于查询 [0, 6], s[0…6] = “0001111” 的所有子字符串中,除 s[0…5] = “000111” 和
s[0…6] = “0001111” 外,其余子字符串都满足 k 约束。
示例 2:
输入:s = “010101”, k = 1, queries = [[0,5],[1,4],[2,3]]
输出:[15,9,3]
解释:
s 的所有子字符串中,长度大于 3 的子字符串都不满足 k 约束。
提示:
1 <= s.length <= 105
s[i] 是 ‘0’ 或 ‘1’
1 <= k <= s.length
1 <= queries.length <= 105
queries[i] == [li, ri]
0 <= li <= ri < s.length
所有查询互不相同
题解:
方法:滑动窗口+前缀和+二分查找
class Solution {public long[] countKConstraintSubstrings(String S, int k, int[][] queries) {char[] s = S.toCharArray();int n = s.length;int[] left = new int[n];long[] sum = new long[n + 1];int[] cnt = new int[2];int l = 0;for (int i = 0; i < n; i++) {cnt[s[i] & 1]++;while (cnt[0] > k && cnt[1] > k) {cnt[s[l++] & 1]--;}left[i] = l; // 记录合法子串右端点 i 对应的最小左端点 l// 计算 i-left[i]+1 的前缀和sum[i + 1] = sum[i] + i - l + 1;}long[] ans = new long[queries.length];for (int i = 0; i < queries.length; i++) {int ql = queries[i][0];int qr = queries[i][1];// 如果区间内所有数都小于 ql,结果是 j=qr+1int j = lowerBound(left, ql - 1, qr + 1, ql);ans[i] = sum[qr + 1] - sum[j] + (long) (j - ql + 1) * (j - ql) / 2;}return ans;}// 返回在开区间 (left, right) 中的最小的 j,满足 nums[j] >= target// 如果没有这样的数,返回 right// 原理见 https://www.bilibili.com/video/BV1AP41137w7/private int lowerBound(int[] nums, int left, int right, int target) {while (left + 1 < right) { // 区间不为空// 循环不变量:// nums[left] < target// nums[right] >= targetint mid = left + (right - left) / 2;if (nums[mid] < target) {left = mid; // 范围缩小到 (mid, right)} else {right = mid; // 范围缩小到 (left, mid)}}return right;}
}方法:预处理
class Solution {public long[] countKConstraintSubstrings(String S, int k, int[][] queries) {char[] s = S.toCharArray();int n = s.length;int[] left = new int[n];long[] sum = new long[n + 1];int[] cnt = new int[2];int l = 0;for (int i = 0; i < n; i++) {cnt[s[i] & 1]++;while (cnt[0] > k && cnt[1] > k) {cnt[s[l++] & 1]--;}left[i] = l;sum[i + 1] = sum[i] + i - l + 1;}int[] right = new int[n];l = 0;for (int i = 0; i < n; i++) {while (l < n && left[l] < i) {l++;}right[i] = l;}long[] ans = new long[queries.length];for (int i = 0; i < queries.length; i++) {int ql = queries[i][0];int qr = queries[i][1];int j = Math.min(right[ql], qr + 1);ans[i] = sum[qr + 1] - sum[j] + (long) (j - ql + 1) * (j - ql) / 2;}return ans;}
}
14.统计好节点的数目
题目链接:3249. 统计好节点的数目
现有一棵 无向 树,树中包含 n 个节点,按从 0 到 n - 1 标记。树的根节点是节点 0 。给你一个长度为 n - 1 的二维整数数组 edges,其中 edges[i] = [ai, bi] 表示树中节点 ai 与节点 bi 之间存在一条边。
如果一个节点的所有子节点为根的
子树
包含的节点数相同,则认为该节点是一个 好节点。
返回给定树中 好节点 的数量。
子树 指的是一个节点以及它所有后代节点构成的一棵树。
示例 1:
输入:edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]]
输出:7
说明:
树的所有节点都是好节点。
示例 2:
输入:edges = [[0,1],[1,2],[2,3],[3,4],[0,5],[1,6],[2,7],[3,8]]
输出:6
说明:
树中有 6 个好节点。上图中已将这些节点着色。
示例 3:
输入:edges =
[[0,1],[1,2],[1,3],[1,4],[0,5],[5,6],[6,7],[7,8],[0,9],[9,10],[9,12],[10,11]]输出:12
解释:
除了节点 9 以外其他所有节点都是好节点。
提示:
2 <= n <= 105
edges.length == n - 1
edges[i].length == 2
0 <= ai, bi < n
输入确保 edges 总表示一棵有效的树。
题解:
方法:深度优先搜索
class Solution {public int countGoodNodes(int[][] edges) {int n = edges.length + 1;List<Integer>[] g = new ArrayList[n];Arrays.setAll(g, i -> new ArrayList<>());for (int[] e : edges) {int x = e[0];int y = e[1];g[x].add(y);g[y].add(x);}dfs(0, -1, g);return ans;}private int ans;private int dfs(int x, int fa, List<Integer>[] g) {int size = 1;int sz0 = 0;boolean ok = true;for (int y : g[x]) {if (y == fa) {continue; // 不能递归到父节点}int sz = dfs(y, x, g);if (sz0 == 0) {sz0 = sz; // 记录第一个儿子子树的大小} else if (sz != sz0) { // 存在大小不一样的儿子子树ok = false; // 注意不能 break,其他子树 y 仍然要递归}size += sz;}ans += ok ? 1 : 0;return size;}
}
15.最少翻转次数使二进制矩阵回文 I
题目链接:3239. 最少翻转次数使二进制矩阵回文 I
给你一个 m x n 的二进制矩阵 grid 。
如果矩阵中一行或者一列从前往后与从后往前读是一样的,那么我们称这一行或者这一列是 回文 的。
你可以将 grid 中任意格子的值 翻转 ,也就是将格子里的值从 0 变成 1 ,或者从 1 变成 0 。
请你返回 最少 翻转次数,使得矩阵 要么 所有行是 回文的 ,要么所有列是 回文的 。
示例 1:
输入:grid = [[1,0,0],[0,0,0],[0,0,1]]
输出:2
解释:
将高亮的格子翻转,得到所有行都是回文的。
示例 2:
输入:grid = [[0,1],[0,1],[0,0]]
输出:1
解释:
将高亮的格子翻转,得到所有列都是回文的。
示例 3:
输入:grid = [[1],[0]]
输出:0
解释:
所有行已经是回文的。
提示:
m == grid.length
n == grid[i].length
1 <= m * n <= 2 * 105
0 <= grid[i][j] <= 1
题解:
方法:回文
class Solution {public int minFlips(int[][] grid) {int m = grid.length;int n = grid[0].length;int diffRow = 0;for (int[] row : grid) {for (int j = 0; j < n / 2; j++) {if (row[j] != row[n - 1 - j]) {diffRow++;}}}int diffCol = 0;for (int j = 0; j < n; j++) {for (int i = 0; i < m / 2; i++) {if (grid[i][j] != grid[m - 1 - i][j]) {diffCol++;}}}return Math.min(diffRow, diffCol);}
}
16.最少翻转次数使二进制矩阵回文 II
题目链接:3240. 最少翻转次数使二进制矩阵回文 II
给你一个 m x n 的二进制矩阵 grid 。
如果矩阵中一行或者一列从前往后与从后往前读是一样的,那么我们称这一行或者这一列是 回文 的。
你可以将 grid 中任意格子的值 翻转 ,也就是将格子里的值从 0 变成 1 ,或者从 1 变成 0 。
请你返回 最少 翻转次数,使得矩阵中 所有 行和列都是 回文的 ,且矩阵中 1 的数目可以被 4 整除 。
示例 1:
输入:grid = [[1,0,0],[0,1,0],[0,0,1]]
输出:3
解释:
示例 2:
输入:grid = [[0,1],[0,1],[0,0]]
输出:2
解释:
示例 3:
输入:grid = [[1],[1]]
输出:2
解释:
提示:
m == grid.length
n == grid[i].length
1 <= m * n <= 2 * 105
0 <= grid[i][j] <= 1
题解:
方法:贪心
class Solution {public int minFlips(int[][] a) {int m = a.length;int n = a[0].length;int ans = 0;for (int i = 0; i < m / 2; i++) {for (int j = 0; j < n / 2; j++) {int cnt1 = a[i][j] + a[i][n - 1 - j] + a[m - 1 - i][j] + a[m - 1 - i][n - 1 - j];ans += Math.min(cnt1, 4 - cnt1); // 全为 1 或全为 0}}if (m % 2 > 0 && n % 2 > 0) {// 正中间的数必须是 0ans += a[m / 2][n / 2];}int diff = 0;int cnt1 = 0;if (m % 2 > 0) {// 统计正中间这一排for (int j = 0; j < n / 2; j++) {if (a[m / 2][j] != a[m / 2][n - 1 - j]) {diff++;} else {cnt1 += a[m / 2][j] * 2;}}}if (n % 2 > 0) {// 统计正中间这一列for (int i = 0; i < m / 2; i++) {if (a[i][n / 2] != a[m - 1 - i][n / 2]) {diff++;} else {cnt1 += a[i][n / 2] * 2;}}}return ans + (diff > 0 ? diff : cnt1 % 4);}
}
17.适龄的朋友
题目链接:825. 适龄的朋友
在社交媒体网站上有 n 个用户。给你一个整数数组 ages ,其中 ages[i] 是第 i 个用户的年龄。
如果下述任意一个条件为真,那么用户 x 将不会向用户 y(x != y)发送好友请求:
ages[y] <= 0.5 * ages[x] + 7
ages[y] > ages[x]
ages[y] > 100 && ages[x] < 100
否则,x 将会向 y 发送一条好友请求。
注意,如果 x 向 y 发送一条好友请求,y 不必也向 x 发送一条好友请求。另外,用户不会向自己发送好友请求。
返回在该社交媒体网站上产生的好友请求总数。
示例 1:
输入:ages = [16,16]
输出:2
解释:2 人互发好友请求。
示例 2:
输入:ages = [16,17,18]
输出:2
解释:产生的好友请求为 17 -> 16 ,18 -> 17 。
示例 3:
输入:ages = [20,30,100,110,120]
输出:3
解释:产生的好友请求为 110 -> 100 ,120 -> 110 ,120 -> 100 。
提示:
n == ages.length
1 <= n <= 2 * 104
1 <= ages[i] <= 120
题解:
方法:计数+滑动窗口
class Solution {public int numFriendRequests(int[] ages) {int[] cnt = new int[121];for (int age : ages) {cnt[age]++;}int ans = 0;int ageY = 0;int cntWindow = 0;for (int ageX = 0; ageX < cnt.length; ageX++) {cntWindow += cnt[ageX];if (ageY * 2 <= ageX + 14) { // 不能发送好友请求cntWindow -= cnt[ageY];ageY++;}if (cntWindow > 0) { // 存在可以发送好友请求的用户ans += cnt[ageX] * cntWindow - cnt[ageX];}}return ans;}
}
下接:【题解】—— LeetCode一周小结47
相关文章:

【题解】—— LeetCode一周小结46
🌟欢迎来到 我的博客 —— 探索技术的无限可能! 🌟博客的简介(文章目录) 【题解】—— 每日一道题目栏 上接:【题解】—— LeetCode一周小结45 11.切棍子的最小成本 题目链接:1547. 切棍子的最…...

Java项目实战II基于微信小程序的校运会管理系统(开发文档+数据库+源码)
目录 一、前言 二、技术介绍 三、系统实现 四、核心代码 五、源码获取 全栈码农以及毕业设计实战开发,CSDN平台Java领域新星创作者,专注于大学生项目实战开发、讲解和毕业答疑辅导 一、前言 在充满活力与激情的校园生活中,校运会不仅是…...

python里的数据结构
列表(List) 定义和特点: 列表是一种有序的可变序列,可包含不同类型的元素,如整数、字符串、列表等。可以通过索引访问和修改元素,索引从 0 开始。代码示例: my_list [1, 2, apple, [4, 5]] pr…...

[Unity Demo]从零开始制作空洞骑士Hollow Knight第二十一集:制作游戏的金钱系统吉欧Geo和初步制作HUD Canvas的额外内容
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、制作游戏的金钱系统吉欧Geo以及HUD Camera 1.制作金钱系统吉欧2.制作吉欧的脚本Geo Counter逻辑处理3.制作HUD Canvas的吉欧的UI4.在敌人的HealthManager.c…...
底层逻辑之:极大似然方法(Maximum Likelihood Estimation, MLE)
简介: 极大似然方法(Maximum Likelihood Estimation, MLE)是一种用于估计统计模型参数的方法。其核心思想是基于观测数据来寻找最可能产生这些数据的模型参数。 早在1821年,德国数学家高斯(C. F. Gauss)就…...

笔记:Centos Nginx Jdk Mysql OpenOffce KkFile Minio安装部署
远程工具 ToDesk Nginx 解压 tar zxvf nginx-1.20.2.tar.gz进入Nginx 文件夹 cd nginx-1.20.2报错解决 ./configure: error: C compiler cc is not found yum -y install gcc gcc-c autoconf automake make./configure: error: the HTTP rewrite module requires the PC…...

【MARL】深入理解多智能体近端策略优化(MAPPO)算法与调参
📢本篇文章是博主强化学习(RL)领域学习时,用于个人学习、研究或者欣赏使用,并基于博主对相关等领域的一些理解而记录的学习摘录和笔记,若有不当和侵权之处,指出后将会立即改正,还望谅…...

深入探索Go语言中的sync.Mutex与sync.RWMutex:原理、应用与实践
深入探索Go语言中的sync.Mutex与sync.RWMutex:原理、应用与实践 在并发编程的世界里,Go语言以其独特的并发模型和简洁的语法赢得了广泛的关注。在Go语言的并发控制工具箱中,sync.Mutex和sync.RWMutex是两个至关重要的工具,它们帮助开发者保护共享资源,避免竞态条件,确保…...

15.postgresql--jsonb 数组进行打平,过滤
用jsonb_array_elements函数先展开数组,再用jsonb_each函数遍历元素中的键值对 例如: SELECT * FROM data_table, LATERAL jsonb_array_elements(json_column) WITH ORDINALITY as elem(element, idx) JOIN LATERAL jsonb_each(elem.element) as kv(ke…...

linux下i2c开发与框架源码分析
目录 1 概述 2 I2c子系统框架 3 I2C的使用流程 3.1 在驱动里使用 3.2 在应用层使用 3.3 I2ctool的使用 4 为硬件i2c注册一个适配器 5 i2c子系统源码流程分析 5.1 i2c device与driver绑定过程 5.1.1 Driver的注册与处理 5.1.2 Client device的生成 5.2 I2c的发送与接…...

[ruby on rails] 安装docker
1. docker安装 ubuntu14.04后自带docker安装包,可以直接安装docker.io sudo apt-get updatesudo apt-get install -y docker.io # 安装后启动sudo service docker start最新版本docker 安装docker-ce # 官方源 curl -fsSL https://download.docker.com/linux/ubun…...

I2C学习
详情学习 12. I2C通讯 — [野火]Linux基础与应用开发实战指南——基于LubanCat-RK系列板卡 文档 (embedfire.com) 问题 i2c总线中scl和sda两条线的作用以及区别 在 I2C 总线(Inter-Integrated Circuit)中,SCL 和 SDA 是两条核心信号线&am…...

VUE:基于MVVN的前端js框架
文章目录 vue框架v-show vue框架 注意是 先写函数名,再写function。 handle:function (){}下面是错误的 function:handle(){}3 v-show 本质上等于号后面还是判断条件,所以不能写赋值语句,下面是正确的 下面是错误的 v-show " ge…...

06、Spring AOP
在我们接下来聊Spring AOP之前我们先了解一下设计模式中的代理模式。 一、代理模式 代理模式是23种设计模式中的一种,它属于结构型设计模式。 对于代理模式的理解: 程序中对象A与对象B无法直接交互,如:有人要找某个公司的老总得先打前台登记传达程序中某个功能需要在原基…...

c语言学习26字符串的应用
字符串在stm32串口中的应用 串口控制流水灯 pc通过串口发送字符串命令控制流水灯 open 流水灯打开 close 流水灯关闭 speed 1~9速度控制 if(strcmp((char *)usart1_rec_buff,"open")0) { led_flag 1; } else if(strcmp((char *)usart1_rec_buff,"close&qu…...

法语旅游常用口语-柯桥学外语到蓝天广场泓畅学校
以下是一些实用的法语旅游常用口语,帮助你在法国旅行时能够进行基本的交流: 问候与道别 Bonjour: 用于日常问候。Au revoir: 用于告别。 请求帮助 S’il vous plat: 用于请求帮助,例如在需要寻找某个地点或服务时。 询问信息 Excusez-moi: 用…...

Kafka 生产者优化与数据处理经验
Kafka:分布式消息系统的核心原理与安装部署-CSDN博客 自定义 Kafka 脚本 kf-use.sh 的解析与功能与应用示例-CSDN博客 Kafka 生产者全面解析:从基础原理到高级实践-CSDN博客 Kafka 生产者优化与数据处理经验-CSDN博客 Kafka 工作流程解析:…...
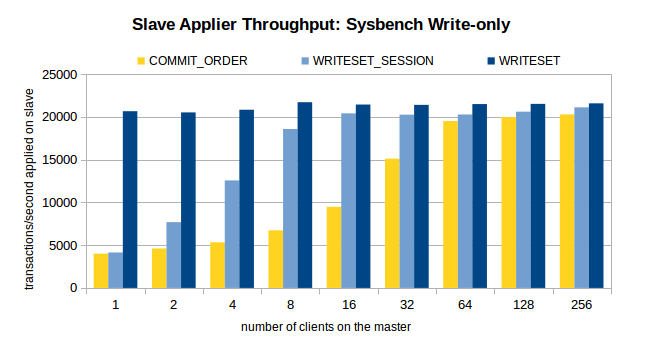
MySQL 主从复制之多线程复制
一、MySQL 多线程复制的背景 MySQL 的主从复制延迟一直是受开发者最为关注的问题之一,MySQL 从 5.6 版本开始追加了并行复制功能,目的就是为了改善复制延迟问题,并行复制称为enhanced multi-threaded slave(简称MTS)。…...

Linux2.6内核进程调度队列
文章目录 前言运行队列 runqueue优先级活动队列过期队列活跃队列 VS 过期队列active指针和expired指针O(1)调度算法 前言 在前面学习并认识了进程之后,我们会发出一个疑问:Linux内核是如何调度进程的呢? 接下来我们就以Linux2.6内核为例深入探…...

Infineon(英飞凌) TLE985xQX 芯片电机工作电流、电压AD采样
其他系列文章导航 Java基础合集数据结构与算法合集 设计模式合集 多线程合集 分布式合集 单片机芯片合集 文章目录 其他系列文章导航 文章目录 前言 一、选取合适的端口 1.通过 OP1、OP2 电流采集运放输入端口进行H桥驱动的电流采集。 2.通过 O_D_VBAT_AD_EN、I_A_VBAT_A…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

Python异步编程:深入理解协程的原理与实践指南
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 持续学习,不断…...

统计按位或能得到最大值的子集数目
我们先来看题目描述: 给你一个整数数组 nums ,请你找出 nums 子集 按位或 可能得到的 最大值 ,并返回按位或能得到最大值的 不同非空子集的数目 。 如果数组 a 可以由数组 b 删除一些元素(或不删除)得到,…...









