回溯法基础入门解析
回溯法
前 言
回溯法也可以叫做回溯搜索法,它是一种搜索的方式。回溯是递归的副产品,只要有递归就会有回溯。回溯法,一般可以解决如下几种问题:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 棋盘问题:N皇后,解数独等等
回溯法模板:
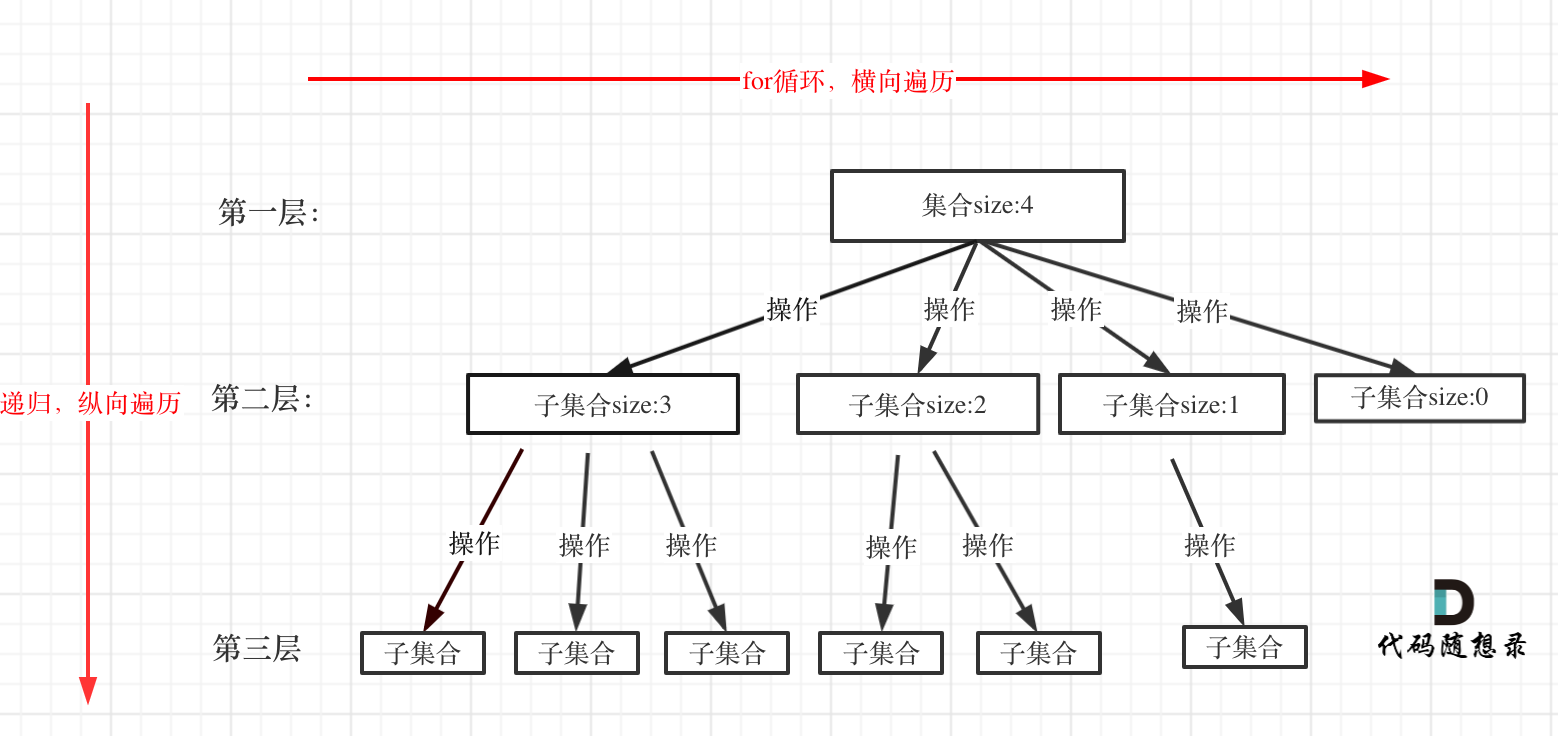
void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果}
}
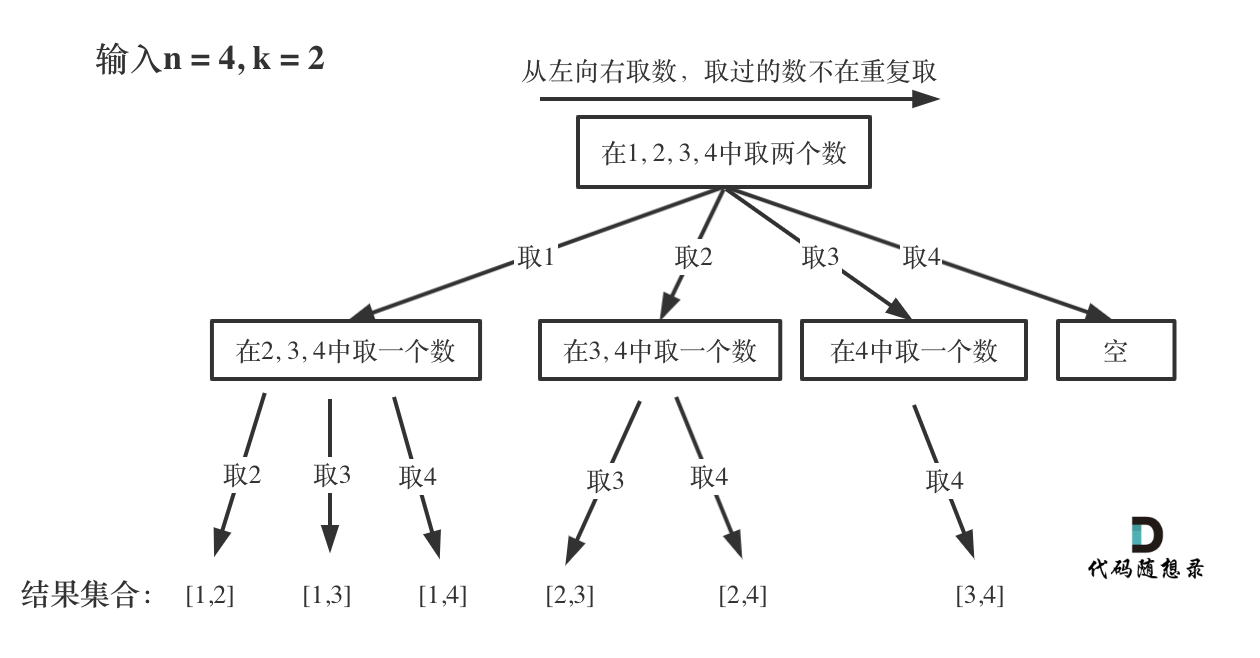
77. 组合
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
示例 1:
输入:n = 4, k = 2
输出:
[[2,4],[3,4],[2,3],[1,2],[1,3],[1,4],
]
示例 2:
输入:n = 1, k = 1
输出:[[1]]
解题:
class Solution {
public:vector<vector<int>> res;// 存放符合条件结果的集合vector<int> path;// 用来存放符合条件结果void assemble(int n, int k, int index){if(path.size()==k){res.push_back(path);//存放结果return;}//剪枝处理i<=n-(k-path.size())+1for(int i=index; i<=n-(k-path.size())+1; i++){//不剪枝就是 … i<=n …path.push_back(i); // 处理节点assemble(n, k, i+1);// 递归path.pop_back();// 回溯,撤销处理的节点}return;}vector<vector<int>> combine(int n, int k) {assemble(n, k, 1);return res;}
};
216. 组合总和 III
找出所有相加之和为 n 的 k 个数的组合,且满足下列条件:
- 只使用数字1到9
- 每个数字 最多使用一次
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。
示例 1:
输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。
示例 2:
输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
解释:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
没有其他符合的组合了。
class Solution {
public:vector<vector<int>> res;vector<int> path;void find(int k, int n, int sum, int index){if(sum>n) return;//剪枝处理if(path.size()==k && sum ==n){res.push_back(path);return;}for(int i=index; i<=9-(k-path.size())+1; i++){//剪枝处理,避免相同元素重复操作sum+=i;path.push_back(i);find(k,n,sum,i+1);sum-=i; path.pop_back();}return;}vector<vector<int>> combinationSum3(int k, int n) {find(k,n,0,1);return res;}
};
17. 电话号码的字母组合
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。

示例 1:
输入:digits = "23"
输出:["ad","ae","af","bd","be","bf","cd","ce","cf"]
示例 2:
输入:digits = ""
输出:[]
class Solution {
public:vector<string> res;string find;const vector<string> anjian={" ", " ", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};//需要设计一个存放号码对应字符的数组void phoneStr(string digits, int length){if(length==digits.size()){res.push_back(find);return;}string keyVal=anjian[digits[length]-'0'];for(int i=0; i<keyVal.size(); i++){//不需要剪枝处理,一个个列举find.push_back(keyVal[i]);phoneStr(digits, length+1);find.pop_back();}}vector<string> letterCombinations(string digits) {if(digits.empty()) return{};phoneStr(digits, 0);return res;}
};
39. 组合总和
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
示例 1:
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选, 7 = 7 。
仅有这两种组合。
示例 2:
输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]
注意
index的使用
class Solution {
public:vector<vector<int>> res;vector<int> path;void find(vector<int>& candidates, int target, int sum, int index){if(sum>target){return;}if(sum==target){res.push_back(path);return;}//i=index是为了保证输出的都是有序的数组,确保输出结果的唯一性for(int i=index; i<candidates.size(); i++){//剪枝处理就是先在主函数对candidates排序,然后判断sum + candidates[i] <= target;sum+=candidates[i];path.push_back(candidates[i]);find(candidates, target, sum, i);//如果是(i+1), 则保证了输出结果每个元素的唯一性sum-=candidates[i];path.pop_back();}}vector<vector<int>> combinationSum(vector<int>& candidates, int target) {find(candidates, target, 0, 0);return res;}
};
40. 组合总和 II
给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的每个数字在每个组合中只能使用 一次 。**注意:**解集不能包含重复的组合。
示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]
class Solution {
public:vector<vector<int>> res;vector<int> path;void find(vector<int>& candidates, int target, int index, int sum){if(sum>target) {return;}//剪枝if(sum==target){res.push_back(path);return;}for(int i = index; i<candidates.size()&&sum+candidates[i]<=target; i++){剪枝//子树里可以不跳过,同一层树里跳过相同元素if(i>index && candidates[i]==candidates[i-1]) {continue;}sum+=candidates[i];path.push_back(candidates[i]); find(candidates, target, i+1, sum);//index+1保证每个数只用一次sum-=candidates[i];path.pop_back();}}vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {sort(candidates.begin(), candidates.end());find(candidates, target, 0, 0);return res;}
};
131. 分割回文串
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是 回文串。返回s所有可能的分割方案。
示例 1:
输入:s = "aab"
输出:[["a","a","b"],["aa","b"]]
示例 2:
输入:s = "a"
输出:[["a"]]
class Solution {
public:vector<vector<string>> res;vector<string> path;void backfind(string& s, int index){//通过index进行切割if(index>=s.size()){res.push_back(path);return;}for(int i=index; i<s.size(); i++){if(isHuiwen(s,index,i)){string str=s.substr(index, i-index+1);//index是留给后面元素开头用的,所以这里不包含i,故'+1'path.push_back(str);backfind(s,i+1);path.pop_back();}else{continue;}}}bool isHuiwen(string s, int begin, int end){//判断回文for(int i=begin,j=end; i<j; i++, j--){if(s[i]!=s[j]){return false;}}return true;}vector<vector<string>> partition(string s) {backfind(s, 0);return res;}
};
93. 复原 IP 地址
有效 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 '.' 分隔。
- 例如:
"0.1.2.201"和"192.168.1.1"是 有效 IP 地址,但是"0.011.255.245"、"192.168.1.312"和"192.168@1.1"是 无效 IP 地址。
给定一个只包含数字的字符串 s ,用以表示一个 IP 地址,返回所有可能的有效 IP 地址,这些地址可以通过在 s 中插入 '.' 来形成。你 不能 重新排序或删除 s 中的任何数字。你可以按 任何 顺序返回答案。
示例 1:
输入:s = "25525511135"
输出:["255.255.11.135","255.255.111.35"]
示例 2:
输入:s = "0000"
输出:["0.0.0.0"]
class Solution {
public:vector<string> res;//存放结果int pointnum=0;//加入的'.'数量void backFindip(string s, int index){if(pointnum==3){//加入的'.'数量为3个,已分割出4段了if(ifIPnum(s,index,s.size()-1)){//判断剩下一段字符是否合个res.push_back(s);return;}return;}for(int i=index; i<s.size(); i++){if(ifIPnum(s,index,i)){//如果这个字符串合格pointnum++;s.insert(s.begin()+i+1,'.');//会在这个后面加上'.'进行分割backFindip(s, i+2);//递归,因为插入'.' 所以+2跳到'.'的后面pointnum--;//回溯s.erase(s.begin()+i+1);//回溯去除'.'}}}bool ifIPnum(string s, int begin, int end){if (begin > end) return false;//防止越界,关键if(s[begin]=='0'&& begin != end){return false;//判断前导0}int num=0;for(int i=begin; i<=end; i++){if(s[i]>'9'||s[i]<'0'){return false;}num = num*10 + (s[i]-'0');if(num>255){return false;}}return true;}vector<string> restoreIpAddresses(string s) {backFindip(s,0);return res;}
};
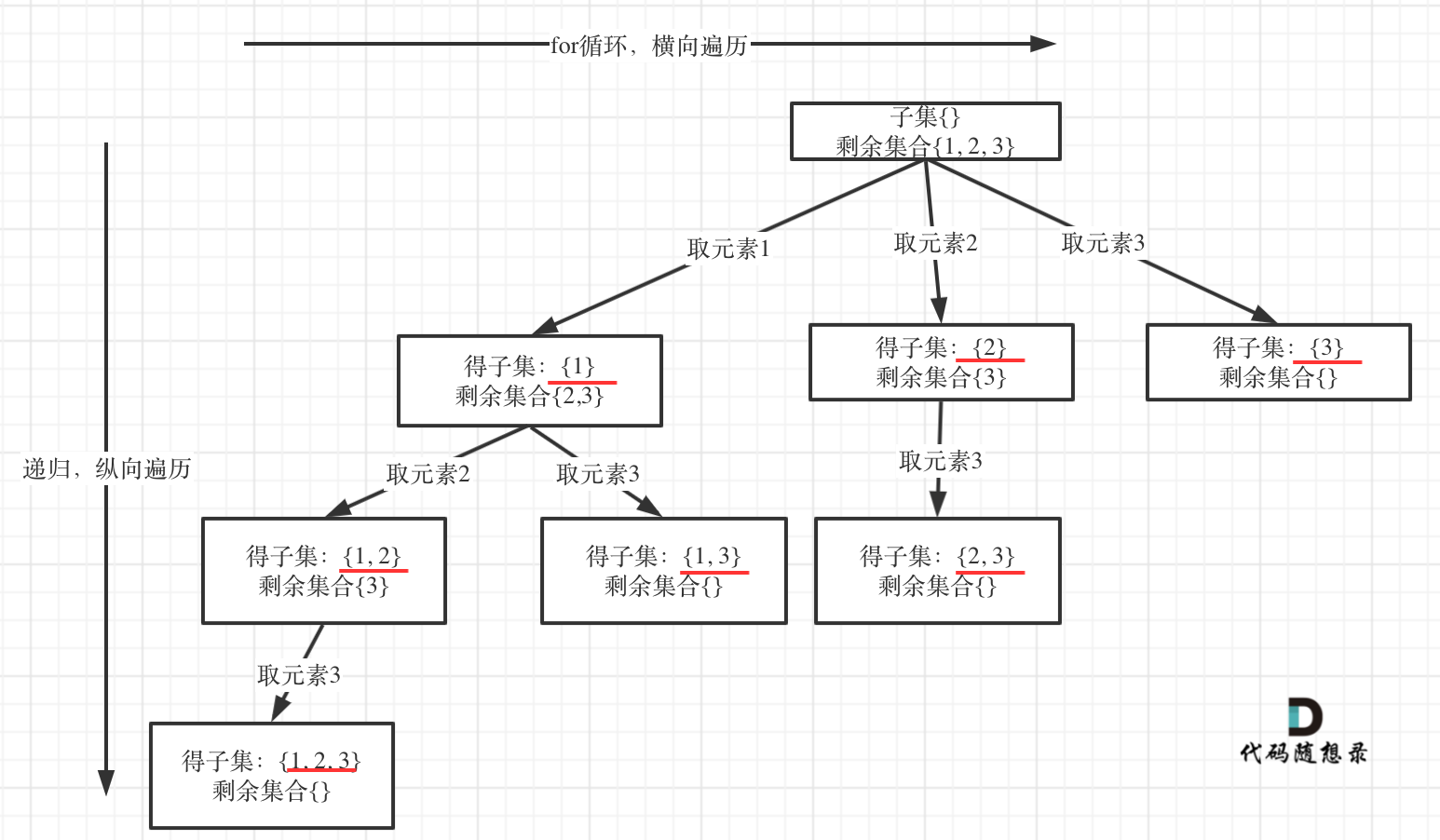
78. 子集
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入:nums = [1,2,3]
输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
示例 2:
输入:nums = [0]
输出:[[],[0]]
class Solution {
public:vector<vector<int>> res;vector<int> path;void find(vector<int>& nums, int index){if(index>=nums.size()){return;}for(int i=index; i<nums.size(); i++){path.push_back(nums[i]);res.push_back(path);find(nums, i+1);path.pop_back();}return;}vector<vector<int>> subsets(vector<int>& nums) {res.push_back(path);find(nums,0);return res;}
};
90. 子集 II
给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的 子集(幂集)。
解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 排列。
示例 1:
输入:nums = [1,2,2]
输出:[[],[1],[1,2],[1,2,2],[2],[2,2]]
示例 2:
输入:nums = [0]
输出:[[],[0]]
class Solution {
public:vector<vector<int>> res;vector<int> path;void backfind(vector<int>& nums, int index, vector<bool>& used){if(index>nums.size()){return;}for(int i=index; i<nums.size(); i++){if(i>0&&nums[i]==nums[i-1]&&used[i-1]==false){continue;}//去重里面的used判断,必须是used[i-1]==false,是上一个的path.push_back(nums[i]);res.push_back(path);used[i]=true;//used放的是i,不是nums[i]backfind(nums, i+1, used);path.pop_back();used[i]=false;}return;}vector<vector<int>> subsetsWithDup(vector<int>& nums) {sort(nums.begin(), nums.end());vector<bool> used(nums.size(),false);res.push_back(path);backfind(nums, 0, used);return res;}
};
相关文章:

回溯法基础入门解析
回溯法 前 言 回溯法也可以叫做回溯搜索法,它是一种搜索的方式。回溯是递归的副产品,只要有递归就会有回溯。回溯法,一般可以解决如下几种问题: 组合问题:N个数里面按一定规则找出k个数的集合切割问题:一…...
计算机网络-VPN虚拟专用网络概述
前面我们学习了在企业内部的二层交换机网络、三层路由网络包括静态路由、OSPF、IS-IS、NAT等,现在开始学习下VPN(Virtual Private Network,虚拟专用网络),其实VPN可能很多人听到第一反应就是梯子,但是其实这…...

信创时代的数据库之路:2024 Top10 国产数据库迁移与同步指南
数据库一直是企业数字化和创新的重要基础设施之一。从传统的关系型数据库到非关系型数据库、分析型数据库,再到云数据库和多模数据库,这一领域仍在持续变革中,各种新型数据库产品涌现,数据管理的能力和应用场景也由此得到了扩展。…...

自制游戏:监狱逃亡
第一个游戏,不喜勿喷: #include<bits/stdc.h> #include<windows.h> using namespace std; int xz; int ruond_1(int n){if(xz1){printf("撬开了,但站在你面前的是俄罗斯内务部特种部队的奥摩大帝,你被九把加特…...

小雪时节,阴盛阳衰,注意禁忌
宋张嵲《小雪作》 霜风一夜落寒林,莽苍云烟结岁阴。 把镜渐无勋业念,爱山唯驻隐沦心。 冰花散落衡门静,黄叶飘零一迳深。 世乱身穷无可奈,强将悲慨事微吟。 网络图片:小雪时节 笔者禁不住喟然而叹:“冰…...

CPU性能优化--微操作
x86 架构处理器吧复杂的CISC指令转为简单的RISC微操作。这样做最大的优势是微操作可以乱序执行,一条简单的相加指令--比如ADD,EAX, EBX,只产生一个微操作,而很多复杂指令--比如ADD, EAX 可能会产生两个微操作,一个将数…...

工厂模式
主要解决对象的创建问题 首先是简单工厂 只有一个工厂类,每次有新的产品就需要修改里面接口的内容,违反了封闭原则 //1、定义抽象产品类 class AbstractCar { public:AbstractCar() default;virtual ~AbstractCar() default;virtual void showName(…...

嵌入式系统与OpenCV
目录 一、OpenCV 简介 二、嵌入式 OpenCV 的安装方法 1. Ubuntu 系统下的安装 2. 嵌入式 ARM 系统中的安装 3. Windows10 和树莓派系统下的安装 三、嵌入式 OpenCV 的性能优化 1. 介绍嵌入式平台上对 OpenCV 进行优化的必要性。 2. 利用嵌入式开发工具,如优…...
编程之路,从0开始:动态内存笔试题分析
Hello大家好,很高兴我们又见面啦! 给生活添点passion,开始今天的编程之路。 今天我们来看几个经典的动态内存笔试题。 1、题目1 #define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<string.h> void GetMemory(char* …...
物联网研究实训室建设方案
一、引言 随着物联网技术的快速发展,其在各个行业的应用越来越广泛,对物联网专业人才的需求也日益增加。为满足这一需求,建设一个符合现代化教学需求的物联网研究实训室,对于提高学生的实践能力和创新能力具有重要意义。本方案旨…...
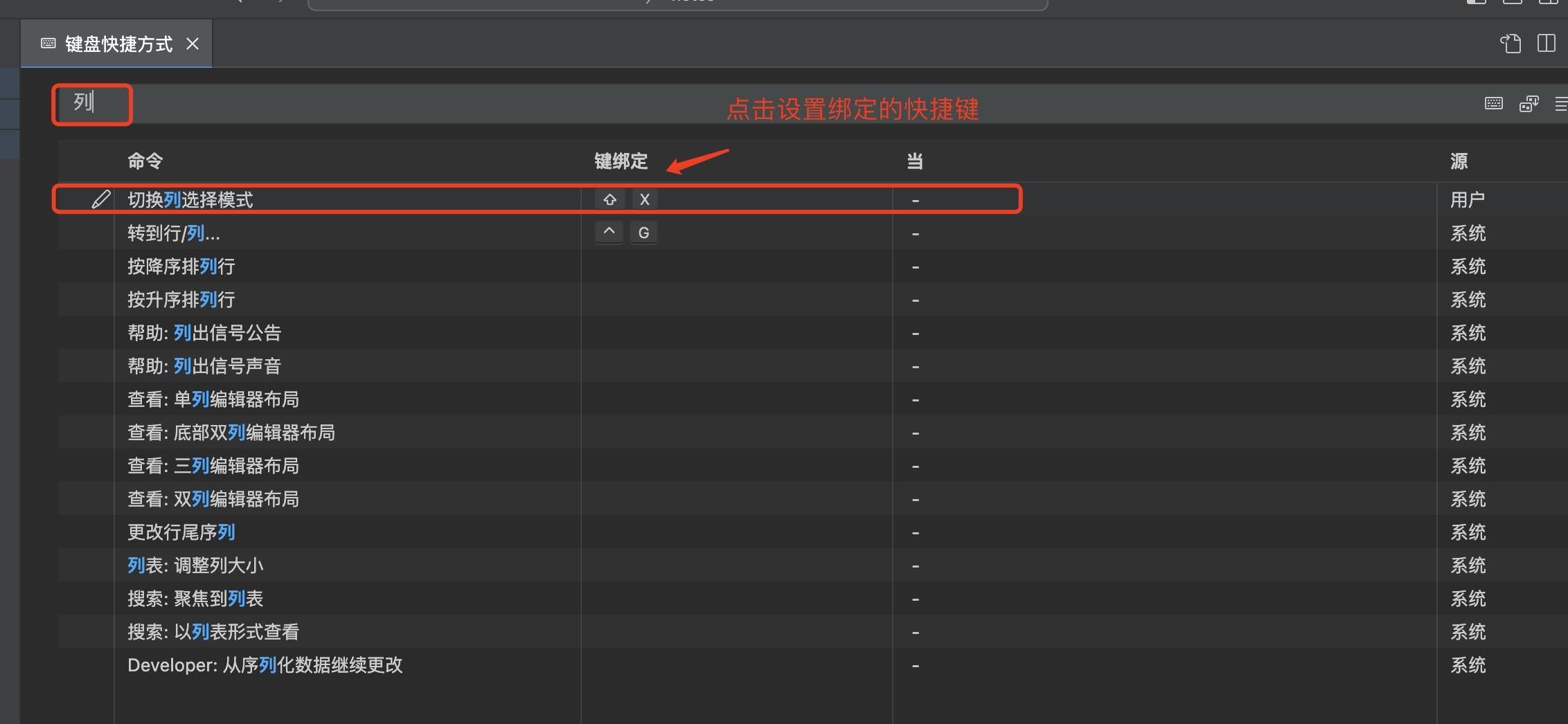
Mac vscode 激活列编辑模式
列编辑模式在批量处理多行文本时,非常有效,但 vscode 默认情况下,又没有激活,因此记录一下启动方法: 激活列编辑模式 然后就可以使用 Alt(Mac 上是 Option 或 Command 键) 鼠标左键 滑动选择了…...

深度学习:GPT-1的MindSpore实践
GPT-1简介 GPT-1(Generative Pre-trained Transformer)是2018年由Open AI提出的一个结合预训练和微调的用于解决文本理解和文本生成任务的模型。它的基础是Transformer架构,具有如下创新点: NLP领域的迁移学习:通过最…...

前端图像处理(一)
目录 一、上传 1.1、图片转base64 二、图片样式 2.1、图片边框【border-image】 三、Canvas 3.1、把canvas图片上传到服务器 3.2、在canvas中绘制和拖动矩形 3.3、图片(同色区域)点击变色 一、上传 1.1、图片转base64 传统上传: 客户端选择图片…...

unity中:超低入门级显卡、集显(功耗30W以下)运行unity URP管线输出的webgl程序有那些地方可以大幅优化帧率
删除Global Volume: 删除Global Volume是一项简单且高效的优化措施。实测表明,这一改动可以显著提升帧率,甚至能够将原本无法流畅运行的场景变得可用。 更改前的效果: 更改后的效果: 优化阴影和材质: …...

ftdi_sio应用学习笔记 4 - I2C
目录 1. 查找设备 2. 打开设备 3. 写数据 4. 读数据 5. 设置频率 6 验证 6.1 遍历设备 6.2 开关设备 6.3 读写测试 I2C设备最多有6个(FT232H),其他为2个。和之前的设备一样,定义个I2C结构体记录找到的设备。 #define FT…...

如何更好的把控软件测试质量
如何更好的把控软件测试质量 在软件开发过程中,测试是确保软件质量、稳定性和用户体验的重要环节。随着需求的不断变化以及技术的不断进步,如何更好的把控软件测试质量已成为一个不可忽视的话题。本文将从几个维度探讨确保软件质量的方法和方案…...
“漫步北京”小程序及“气象景观数字化服务平台”上线啦
随着科技的飞速发展,智慧旅游已成为现代旅游业的重要趋势。近日,北京万云科技有限公司联合北京市气象服务中心,打造的“气象景观数字化服务平台“和“漫步北京“小程序已经上线,作为智慧旅游的典型代表,以其丰富的功能…...

SOL链上的 Meme 生态发展:从文化到创新的融合#dapp开发#
一、引言 随着区块链技术的不断发展,Meme 文化在去中心化领域逐渐崭露头角。从 Dogecoin 到 Shiba Inu,再到更多细分的 Meme 项目,这类基于网络文化的加密货币因其幽默和社区驱动力吸引了广泛关注。作为近年来备受瞩目的区块链平台之一&…...

身份证实名认证API接口助力电商购物安全
亲爱的网购达人们,你们是否曾经因为网络上的虚假信息和诈骗而感到困扰?在享受便捷的网购乐趣时,如何确保交易安全成为了我们共同关注的话题。今天,一起来了解一下翔云身份证实名认证接口如何为电子商务保驾护航,让您的…...

【过程控制系统】第6章 串级控制系统
目录 6. l 串级控制系统的概念 6.1.2 串级控制系统的组成 6.l.3 串级控制系统的工作过程 6.2 串级控制系统的分析 6.2.1 增强系统的抗干扰能力 6.2.2 改善对象的动态特性 6.2.3 对负荷变化有一定的自适应能力 6.3 串级控制系统的设计 6.3.1 副回路的选择 2.串级系…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...
