归并排序与逆序对问题(C语言版)
一、引言
归并排序是一种高效且稳定的排序方法,而逆序对问题是算法领域的一个经典问题,本文教大家如何实现归并排序,以及如何使用归并排序去结果逆序对问题
二、归并排序
归并排序思想
分解:将待排序的数组分成两半,递归地对这两半进行归并排序,直到每个子数组的大小为1(此时已经是有序的)。
合并:将两个已排序的子数组合并成一个新的有序数组。合并过程通常使用两个指针,分别指向两个子数组的当前元素,比较这两个元素并将较小的元素放入结果数组中,直到所有元素都被合并。
我们借助递归可以很好的实现数据的分解和合并,我们可以借助代码区理解归并排序
#include <stdio.h>#define MAXSIZE 100int merge[MAXSIZE]; void Merge(int a[], int left, int right, int middle) {int i = left; int j = middle + 1; int k = left; while (i <= middle && j <= right) {if (a[i] <= a[j]) {merge[k++] = a[i++]; }else {merge[k++] = a[j++];}}while (i <= middle) {merge[k++] = a[i++];}while (j <= right) {merge[k++] = a[j++];}for (i = left; i <= right; i++) {a[i] = merge[i];}
}void Mergesort(int a[], int left, int right) {if (left < right) {int middle = (left + right) / 2;Mergesort(a, left, middle); Mergesort(a, middle + 1, right); Merge(a, left, right, middle); }
}void show(int a[], int n) {for (int i = 0; i < n; i++) {printf("%d ", a[i]);}printf("\n");
}int main() {int a[MAXSIZE];int n;printf("请输入待排关键字个数(n>0): ");scanf_s("%d", &n);printf("请依次输入关键字的数据值:\n");for (int i = 0; i < n; i++) {scanf_s("%d", &a[i]);}Mergesort(a, 0, n - 1); printf("该组数据排序后的结果: ");show(a, n);printf("该组数据逆序对的个数: %d\n", count); printf("========================================================================================================================");return 0;
}
这段代码便是归并排序的核心代码,其中分解通过递归的方式进行,而合并,我们则定义了一个函数
void Merge(int a[], int left, int right, int middle) {int i = left; int j = middle + 1; int k = left; while (i <= middle && j <= right) {if (a[i] <= a[j]) {merge[k++] = a[i++]; }else {merge[k++] = a[j++];count += (middle - i + 1); }}while (i <= middle) {merge[k++] = a[i++];}while (j <= right) {merge[k++] = a[j++];}for (i = left; i <= right; i++) {a[i] = merge[i];}
}
该函数我们可以实现两个有序函数的合并,合并之后还是有序函数
那么我们如何保证我们要合并的两个数组原本是有序的呢?这就需要我们探究一下递归的本质了
我们通过如下递归,最后会将数组分解为一个一个的单独的数字
void Mergesort(int a[], int left, int right) {if (left < right) {int middle = (left + right) / 2;Mergesort(a, left, middle); Mergesort(a, middle + 1, right); Merge(a, left, right, middle); }
}这些一个一个的数字就是我们最早的有序数组,之后我们通过有序数组产生的数组,也都是有序的,经过我们的拆分和合并,最后就会产生一个合并好的最终的有序数组
这样归并排序的全过程就结束了
三、逆序对
1.何为逆序对
逆序对是指在一个序列中,两个元素的相对位置与它们的大小关系不一致。具体来说,对于一个序列中的两个元素 a[i]a[i] 和 a[j]a[j],如果 i<j i<j 且 a[i]>a[j] a[i]>a[j],那么就称这个对 (a[i],a[j])(a[i],a[j]) 为一个逆序对。
例如,在序列 [3,1,2][3,1,2] 中:
- 逆序对有 (3,1)(3,1) 和 (3,2)(3,2),因为 33 在 11 和 22 之前,但 33 的值大于它们。
- 而 (1,2)(1,2) 不是逆序对,因为 1<21<2。
逆序对的数量在计算排序算法的复杂度、分析数组的有序性等方面有重要应用。在某些排序算法中,逆序对的数量可以用来衡量数组的“无序程度”。
简而言之,就是前面的数比后面的数大,那么这两个数的下标就构成了逆序对
2.如何用归并思想求取逆序对
代码如下
#include <stdio.h>#define MAXSIZE 100int count = 0;
int merge[MAXSIZE]; void Merge(int a[], int left, int right, int middle) {int i = left; int j = middle + 1; int k = left; while (i <= middle && j <= right) {if (a[i] <= a[j]) {merge[k++] = a[i++]; }else {merge[k++] = a[j++];count += (middle - i + 1); }}while (i <= middle) {merge[k++] = a[i++];}while (j <= right) {merge[k++] = a[j++];}for (i = left; i <= right; i++) {a[i] = merge[i];}
}void Mergesort(int a[], int left, int right) {if (left < right) {int middle = (left + right) / 2;Mergesort(a, left, middle); Mergesort(a, middle + 1, right); Merge(a, left, right, middle); }
}void show(int a[], int n) {for (int i = 0; i < n; i++) {printf("%d ", a[i]);}printf("\n");
}int main() {int a[MAXSIZE];int n;printf("请输入待排关键字个数(n>0): ");scanf_s("%d", &n);printf("请依次输入关键字的数据值:\n");for (int i = 0; i < n; i++) {scanf_s("%d", &a[i]);}Mergesort(a, 0, n - 1); printf("该组数据排序后的结果: ");show(a, n);printf("该组数据逆序对的个数: %d\n", count); printf("========================================================================================================================");return 0;
}
其实逆序对的求取,我们只需要在我们归并排序的基础上加入几行代码便可,其中最核心的是下面的一段
int i = left; int j = middle + 1; int k = left; while (i <= middle && j <= right) {if (a[i] <= a[j]) {merge[k++] = a[i++]; }else {merge[k++] = a[j++];count += (middle - i + 1); }}当我们的右边数组要比左边数组的数小时,便构成了逆序对的条件,但是这样的依次移动会产生几个逆序对呢,我们可以推断一下
我们左边的数列是有序的,当右边的某个数比左边的小时,它比左边那个数组中的右边的数都要小
所以
count += (middle - i + 1); 最后的逆序对的个数便是count的值
四、结语
今天微服务的学习要放在晚上了
相关文章:
)
归并排序与逆序对问题(C语言版)
一、引言 归并排序是一种高效且稳定的排序方法,而逆序对问题是算法领域的一个经典问题,本文教大家如何实现归并排序,以及如何使用归并排序去结果逆序对问题 二、归并排序 归并排序思想 分解:将待排序的数组分成两半,…...

网络爬虫总结与未来方向
通过深入学习和实际操作,网络爬虫技术从基础到进阶得以系统掌握。本节将全面总结关键内容,并结合前沿技术趋势与最新资料,为开发者提供实用性强的深度思考和方案建议。 1. 网络爬虫技术发展趋势 1.1 趋势一:高性能分布式爬虫 随…...

C++ 核心数据结构:Stack 与 Queue 类深度解析
🌟快来参与讨论💬,点赞👍、收藏⭐、分享📤,共创活力社区。 🌟 目录 💯前言 💯Stack 类 (一)Stack 类的概念与特点 (二&#x…...

Python枚举类详解:用enum模块高效管理常量数据
《Python OpenCV从菜鸟到高手》带你进入图像处理与计算机视觉的大门! 在编程中,常量的管理是一个关键环节,合理的管理常量可以提高代码的可读性和可维护性。Python的enum模块提供了一种有效的方式来组织常量数据,通过枚举类(Enum)将相关的常量值集合在一起,使代码更具结…...

企业OA管理系统:Spring Boot技术深度探索
4系统概要设计 4.1概述 本系统采用B/S结构(Browser/Server,浏览器/服务器结构)和基于Web服务两种模式,是一个适用于Internet环境下的模型结构。只要用户能连上Internet,便可以在任何时间、任何地点使用。系统工作原理图如图4-1所示: 图4-1系统工作原理…...

汽车免拆诊断案例 | 2012款路虎揽胜运动版柴油车加速无力
故障现象 一辆2012款路虎揽胜运动版车,搭载3.0T柴油发动机(型号为306DT),累计行驶里程约为10.2万km。车主进厂反映,车辆行驶中加速无力,且发动机故障灯异常点亮。 故障诊断 接车后试车,发动…...

uniapp接入高德地图
下面代码兼容安卓APP和H5 高德地图官网:我的应用 | 高德控制台 ,绑定服务选择《Web端(JS API)》 /utils/map.js 需要设置你自己的key和安全密钥 export function myAMap() {return new Promise(function(resolve, reject) {if (typeof window.onLoadM…...

(UI自动化测试)web自动化测试
web自动化测试 UI自动化测试介绍 自动化测试理论: 图片上的文字等等不能做测试,只能发现固定的bug 工具选择及介绍 浏览器驱动:找元素--核心:驱动(操作元素)--通过代码...

【es6进阶】如何使用Proxy实现自己的观察者模式
观察者模式(Observer mode)指的是函数自动观察数据对象,一旦对象有变化,函数就会自动执行。这里,我们是使用es6的proxy及reflect来实现这个效果。 实现效果 业务分析 源数据 const object2 {name: "张三"…...

住宅IP怎么在指纹浏览器设置运营矩阵账号
矩阵账号的运营已经成为了许多企业和个人推广策略中的重要一环。通过构建和管理多个社交媒体或电商平台的账号,可以有效地扩大品牌影响力,提高市场覆盖率。然而,随着平台对账号关联的限制越来越严格,如何安全、有效地运营这些矩阵…...

表格数据处理中大语言模型的微调优化策略研究
论文地址 Research on Fine-Tuning Optimization Strategies for Large Language Models in Tabular Data Processing 论文主要内容 这篇论文的主要内容是研究大型语言模型(LLMs)在处理表格数据时的微调优化策略。具体来说,论文探讨了以下…...

CentOS7 如何查看kafka topic中的数据
1. 确保 Kafka 服务运行 先检查 Kafka 和 Zookeeper 是否正在运行: systemctl status kafka systemctl status zookeeper 如果没有启动,先启动服务: systemctl start zookeeper systemctl start kafka 2. 进入 Kafka 安装目录 通常 …...

VRRP实现出口网关设备冗余备份
VRRP虚拟路由冗余 vrrp实现设备主备备份 Tips: VRRP能够在不改变组网的情况下,将多台路由器虚拟成一个虚拟路由器,通过配置虚拟路由器的IP地址为默认网关,实现网关的备份。协议版本: VRRPV2 (常用)和VRRPV3:VRRPV2仅适用于IPv4…...

超详细:Redis分布式锁
如何基于 Redis 实现一个最简易的分布式锁? 不论是本地锁还是分布式锁,核心都在于“互斥”。 在 Redis 中, SETNX 命令是可以帮助我们实现互斥。SETNX 即 SET if Not eXists (对应 Java 中的 setIfAbsent 方法),如果 key 不存在…...

Vue与React的Suspense组件对比
在Vue和React中都内置了Suspense组件,该组件用于处理异步组件加载。当Suspense包裹的实际组件内容尚未加载完成时会先展示后备内容,等待组件内容加载完成后再切换成实际组件内容。这可以显著提升用户体验,适用于大数据加载、组件懒加载等场景…...

Spring框架深度剖析:特性、安全与优化
文章目录 Spring框架简介主要特性1. 依赖注入(Dependency Injection, DI)2. 面向切面编程(Aspect-Oriented Programming, AOP)3. 声明式事务管理4. 强大的MVC框架5. 集成测试支持6. 多种数据访问技术的支持 安全性1. 认证…...

硬盘文件误删:全面解析、恢复方案与预防策略
一、硬盘文件误删现象概述 在日常使用电脑的过程中,硬盘文件误删是许多用户都曾遇到过的问题。这种意外的数据丢失,不仅可能让我们辛苦编辑的文档、珍贵的照片和视频等瞬间消失,还可能对工作和生活造成重大影响。硬盘文件误删,如…...
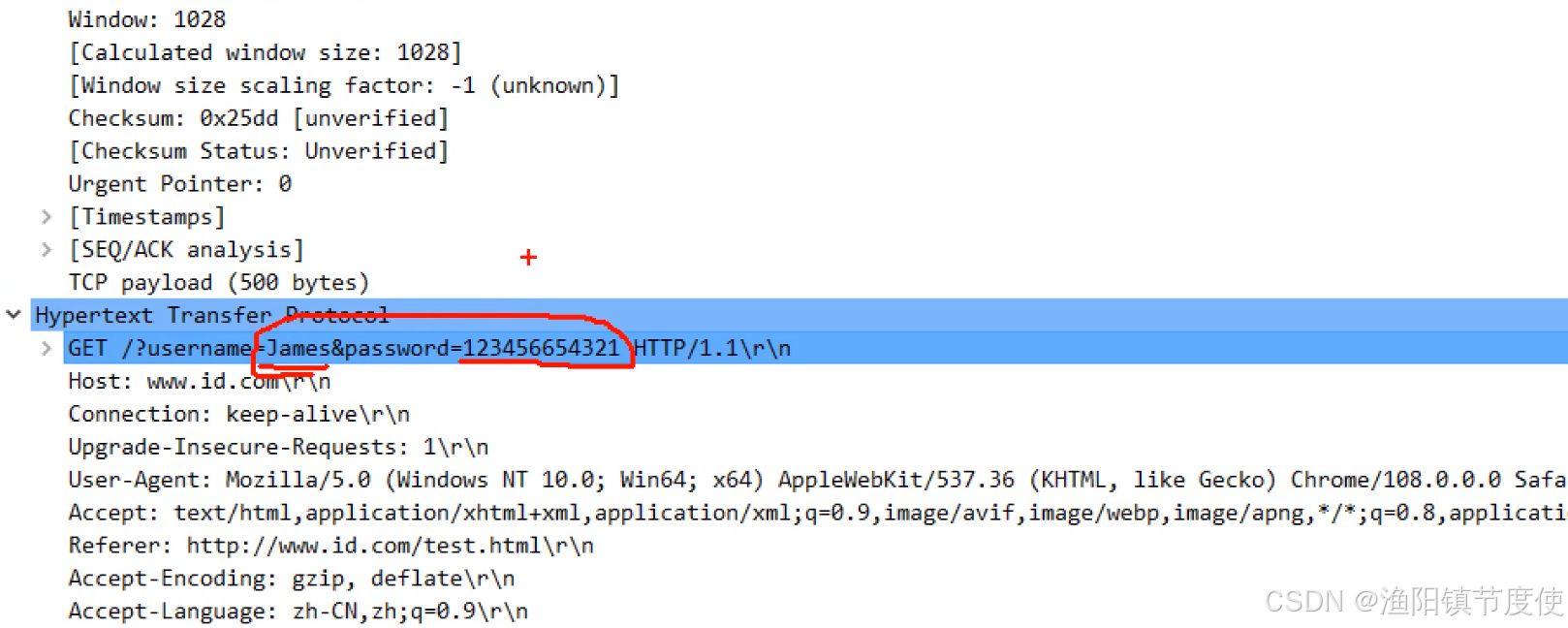
tcpdump抓包 wireShark
TCPdump抓包工具介绍 TCPdump,全称dump the traffic on anetwork,是一个运行在linux平台可以根据使用者需求对网络上传输的数据包进行捕获的抓包工具。 tcpdump可以支持的功能: 1、在Linux平台将网络中传输的数据包全部捕获过来进行分析 2、支持网络层…...
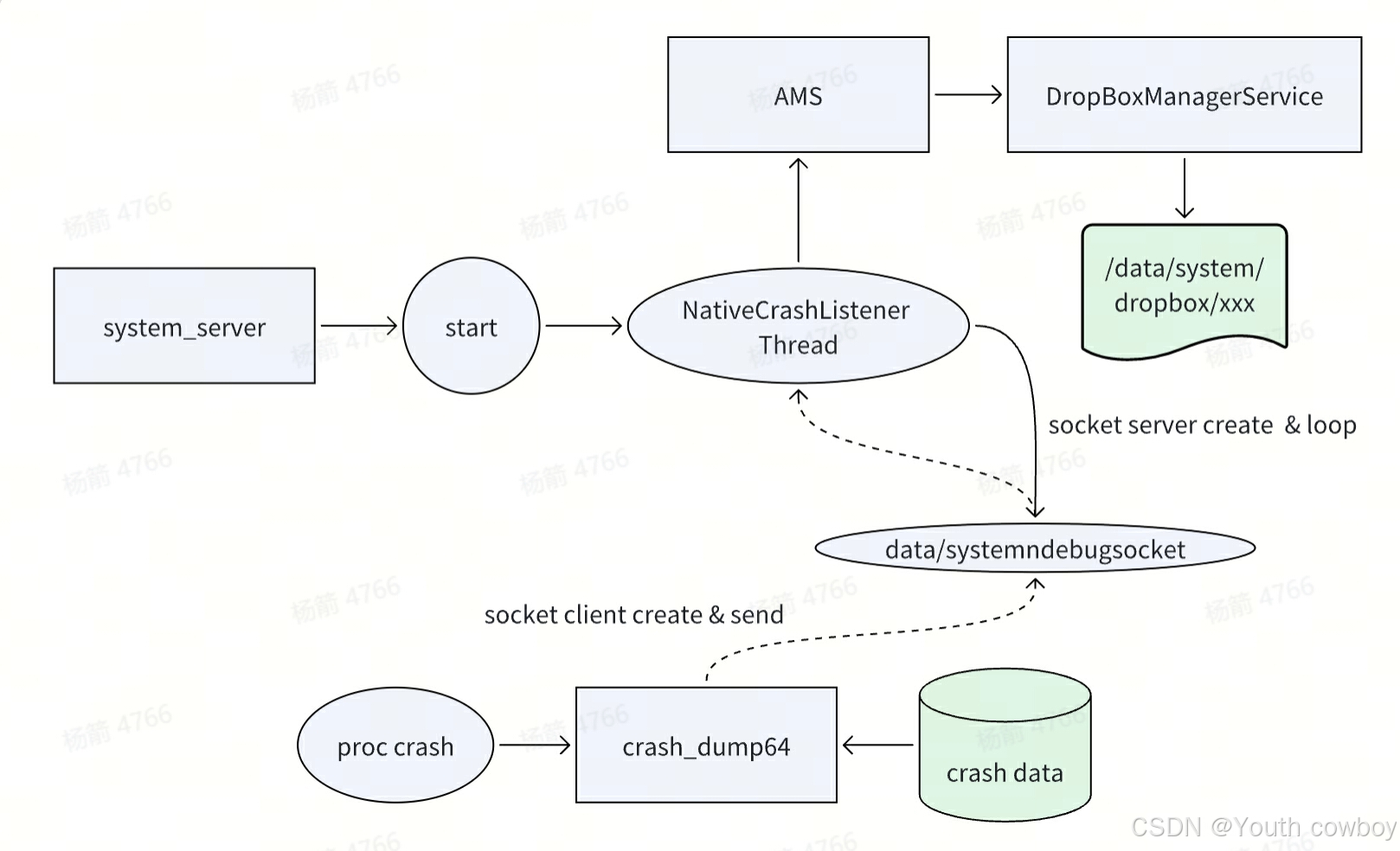
Android system_server进程
目录 一、system_server进程介绍 二、system_server进程启动流程 2.1 startBootstrapServices 2.2 startCoreServices 2.3 startOtherServices 2.4 startApexServices 三、如何使用系统服务 3.1 app进程调用系统服务 3.2 native进程调用系统服务 3.3 system_server进…...

Vue3+element-plus 实现中英文切换(Vue-i18n组件的使用)
1、前言 在 Vue 3 项目中结合 vue-i18n 和 Element Plus 实现中英文切换是一个常见的需求。下面是一个详细的步骤指南,帮助你完成这个任务。 安装引入 1. 安装依赖 首先,你需要安装 vue-i18n 和 Element Plus。 npm install vue-i18nnext element-p…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...
