【LLM】一文学会SPPO
博客昵称:沈小农学编程
作者简介:一名在读硕士,定期更新相关算法面试题,欢迎关注小弟!
PS:哈喽!各位CSDN的uu们,我是你的小弟沈小农,希望我的文章能帮助到你。欢迎大家在评论区唠嗑指正,觉得好的话别忘了一键三连哦!😘
SPPO是强化学习的一种,据猜测今年9月OpenAI最新的大模型O1使用该方法进行微调。SPPO,英文全称Self-Play Preference Optimization,中文为自博弈偏好优化。其受到了纳什均衡的冯·诺依曼两人常和博弈公式以及RLHF+PPO框架的启发,而设计出来。下面本文将讲解SPPO的损失函数、策略梯度更新以及算法框架。
目录
1 策略梯度更新公式
2 损失函数
3 算法流程图
参考文献
1 策略梯度更新公式
常和博弈的纳什均衡公式如下所示:
现在让我们一步步从常和博弈的纳什均衡公式的一般形式推导出 SPPO 算法的策略梯度更新公式。
使用Freund和Schapire(1999)建立一个迭代框架,该框架可以平均渐进收敛到最优策略。
上面的框架具体后,写为
归一化因子为
对上式两边取对数,左右平移变化得
为了简化计算,使用L2距离公式来近似上面的公式计算,得到下面的公式
到这里,策略更新公式就推导出来了。不过这是针对连续数据的。下面我们来推导该公式以应用到离散数据上,同时进一步简化计算。
可能性估计:可以用有限的样本来近似策略更新公式。对于每个提示,我们选取
个回答
作为样本,用
表示经验分布。有限样本优化问题可以近似为:
具体来说,和
。
被视作一种期望,可以通过在偏好项
的总共
个序列中的
个新样本来估计。
我们可以用基于人类偏好模型的常数替换来进一步简化计算。具体来说,用
替换
。假设在任意给定的对中赢的概率是同等机会的,1或者0,当
,我们能得到
。
至此,SPPO的策略更新公式推导完成。
下面让我们来得到策略梯度更新公式。
改写上面的公式为:
RLHF的策略梯度更新公式为:
对比发现上面的公式本质上是策略梯度更新公式,至此推导完成。
2 损失函数
SPPO的损失函数如下:
公式通过胜者策略得分与输者策略得分的平方和,能更全面地评价模型。我们可以进一步简化公式,我们令胜者对输者的胜率为1,输者对胜者的胜率为0,则损失函数可以简化为:
3 算法流程图

参考文献
《Self-Play Preference Optimization for Language Model Alignment》
相关文章:

【LLM】一文学会SPPO
博客昵称:沈小农学编程 作者简介:一名在读硕士,定期更新相关算法面试题,欢迎关注小弟! PS:哈喽!各位CSDN的uu们,我是你的小弟沈小农,希望我的文章能帮助到你。欢迎大家在…...

如何通过ChatGPT提高自己的编程水平
在编程学习的过程中,开发者往往会遇到各种各样的技术难题和学习瓶颈。传统的学习方法依赖书籍、教程、视频等,但随着技术的不断发展,AI助手的崛起为编程学习带来了全新的机遇。ChatGPT,作为一种强大的自然语言处理工具,…...

NVR管理平台EasyNVR多品牌NVR管理工具的流媒体视频融合与汇聚管理方案
随着信息技术的飞速发展,视频监控已经成为现代社会安全管理和业务运营不可或缺的一部分。无论是智慧城市、智能交通、还是大型企业、校园安防,视频监控系统的应用都日益广泛。NVR管理平台EasyNVR,作为功能强大的流媒体服务器软件,…...

python之使用django框架开发web项目
本问将对django框架在python的web项目中的使用进行介绍,有不对之处,烦请指正。 首先使用创建一个django工程(本示例中使用pycharm2024+python3.12),名称和项目保存路径根据自己的需要自行修改,新手直接默认本机环境就好(关于conda将会另开一篇进行讲解。),最后点击cre…...

ChatGPT 桌面版发布了,如何安装?
本章教程教大家如何进行安装。 一、下载安装包 官网地址地址:https://openai.com/chatgpt/desktop/ 支持Windows和MacOS操作系统 二、安装步骤 Windows用户下载之后,会有一个exe安装包,点击运行安装即可。 注意事项,如果Windows操…...

ubuntu 配置 多个 git 客户端 账户
Git配置两个或多个账户 https://blog.csdn.net/mainking2003/article/details/134711865 git 提交 不用输入用户名、密码的方法(GIT免密提交) https://blog.csdn.net/wowocpp/article/details/125797263 git config 用法 https://blog.csdn.net/blueb…...

React Native的界面与交互
React Native (RN) 是一个由 Facebook 开发的开源框架,用于构建跨平台的移动应用程序。它允许开发者使用 JavaScript 和 React 来创建原生 iOS 和 Android 应用。RN 的出现极大地简化了移动应用的开发过程,使得开发者可以更快速、更高效地构建高质量的应…...

autogen+ollama+litellm实现本地部署多代理智能体
autogen 是一个专门为大语言模型 (LLMs) 驱动的自治代理 (autonomous agents) 设计的 Python 库,由 Microsoft 开发和维护。它通过高度模块化和可扩展的架构,支持用户快速构建和运行多代理系统,这些代理可以在没有明确人类干预的情况下协作完成复杂任务。AutoGen 支持以最少…...
InstantStyle容器构建指南
一、介绍 InstantStyle 是一个由小红书的 InstantX 团队开发并推出的图像风格迁移框架,它专注于解决图像生成中的风格化问题,旨在生成与参考图像风格一致的图像。以下是关于 InstantStyle 的详细介绍: 1.技术特点 风格与内容的有效分离 &a…...
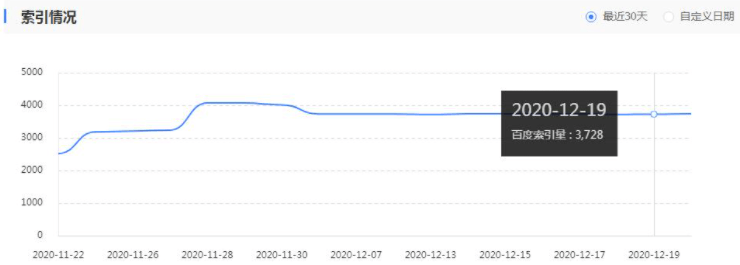
百度主动推送可以提升抓取,它能提升索引量吗?
站长在建站SEO的时候,需要用到百度站长平台(资源平台)的工具,在站长工具中【普通收录】-【资源提交】-【API提交】这个功能,对网站的抓取进行一个提交。 这里估计很多站长就有疑问,如果我主动推送…...

A045-基于spring boot的个人博客系统的设计与实现
🙊作者简介:在校研究生,拥有计算机专业的研究生开发团队,分享技术代码帮助学生学习,独立完成自己的网站项目。 代码可以查看文章末尾⬇️联系方式获取,记得注明来意哦~🌹 赠送计算机毕业设计600…...

JavaEE 【知识改变命运】02 多线程(1)
文章目录 线程是什么?1.1概念1.1.1 线程是什么?1.1.2 为什么要有线程1.1.3 进程和线程的区别1.1.4 思考:执行一个任务,是不是创建的线程或者越多是不是越好?(比如吃包子比赛)1.1.5 ) Java 的线程…...
)
Pytorch使用手册-Transforms(专题四)
Transforms(变换) 在 PyTorch 数据处理中的重要性和使用方法,特别是如何通过 torchvision.transforms 模块对数据进行预处理和变换,使其适合用于训练机器学习模型。以下是具体的内容解读: 什么是 Transforms? 数据通常在收集后并非直接适合用于训练机器学习模型,需要通…...

【Android】ARouter的使用及源码解析
文章目录 简介介绍作用 原理关系 使用添加依赖和配置初始化SDK添加注解在目标界面跳转界面不带参跳转界面含参处理返回结果 源码基本流程getInstance()build()navigation()_navigation()Warehouse ARouter初始化init帮助类根帮助类组帮助类 completion 总结 简介 介绍 ARouter…...

ValueError: bbox_params must be specified for bbox transformations
错误 ValueError: bbox_params must be specified for bbox transformations 是因为使用了需要处理边界框(bboxes)的增强操作,但在 albumentations.Compose 中没有正确设置bbox_params 参数。 bbox_params 是用来指定如何处理边界框的配置。…...

挂壁式空气净化器哪个品牌的质量好?排名top3优秀产品测评分析
随着挂壁式空气净化器市场的不断扩大,各类品牌与型号琳琅满目。但遗憾的是,一些跨界网红品牌过于追求短期效益,导致产品在净化效果与去除异味方面表现平平,使用体验不佳,甚至可能带来二次污染风险,影响人体…...
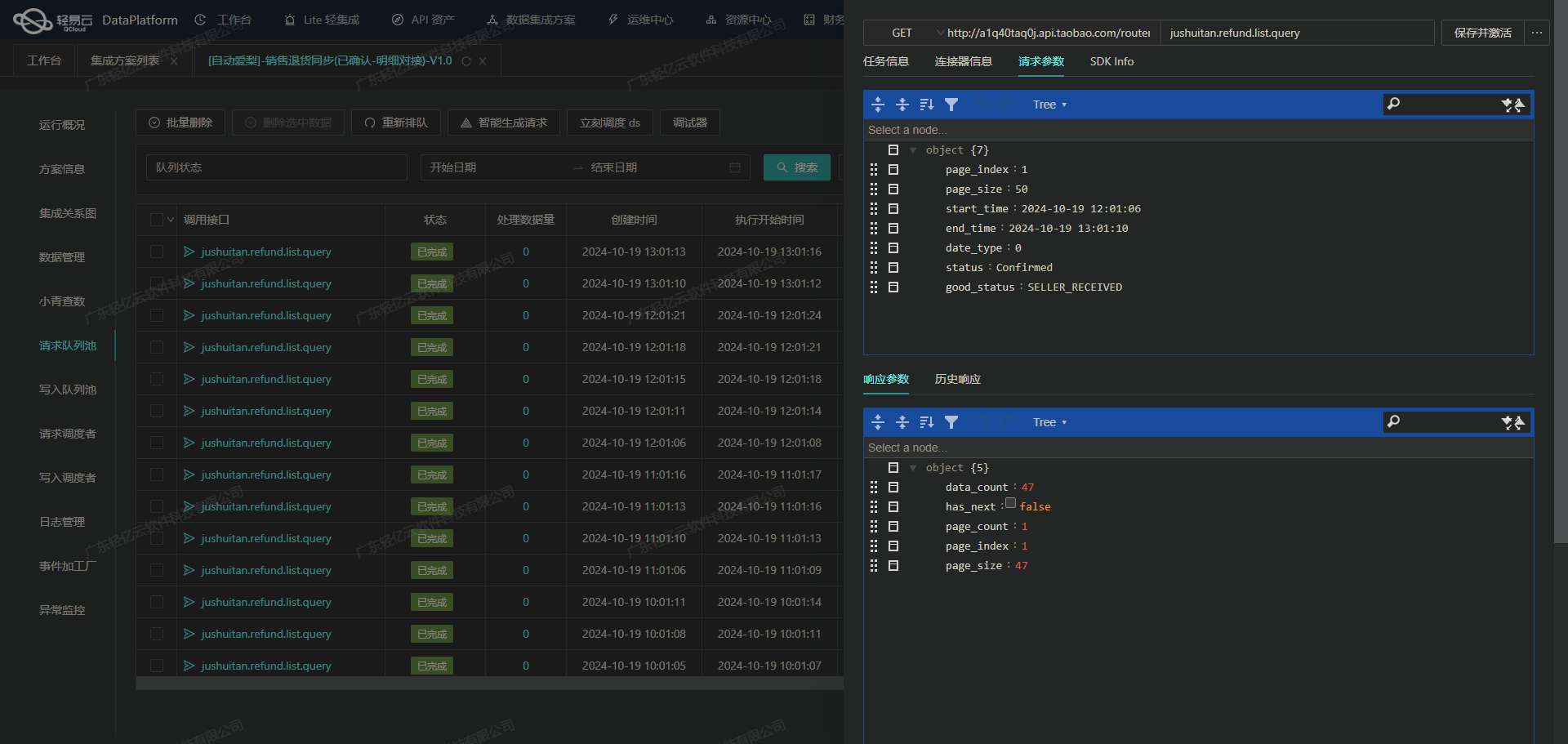
钉钉数据如何高效集成到金蝶云星空系统
钉钉数据集成到金蝶云星空的技术案例分享 在企业日常运营中,办公用品采购流程的高效管理至关重要。为了实现这一目标,我们采用了轻易云数据集成平台,将钉钉中的采购申请单数据无缝对接到金蝶云星空系统中。本次案例将详细解析【办公用品采购…...
)
躺平成长-腾讯云数据库(又消失了一次)
开源竞争: 当你无法彻底掌握技术的时候,你就开源这个技术,形成更多的技术依赖,你会说 这不就是在砸罐子吗?一个行业里面总会有人砸罐子的,你不如先砸罐子,还能听个响声。 数据库的里面清洁的数据…...

初学 flutter 问题记录
windows搭建flutter运行环境 一、运行 flutter doctor遇到的问题 Xcmdline-tools component is missingRun path/to/sdkmanager --install "cmdline-tools;latest"See https://developer.android.com/studio/command-line for more details.1)cmdline-to…...

Hadoop的MapReduce详解
文章目录 Hadoop的MapReduce详解一、引言二、MapReduce的核心概念1、Map阶段1.1、Map函数的实现 2、Reduce阶段2.1、Reduce函数的实现 三、MapReduce的执行流程四、MapReduce的使用实例Word Count示例1. Mapper类2. Reducer类3. 执行Word Count 五、总结 Hadoop的MapReduce详解…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...
