数据结构与算法——1122—复杂度总结检测相同元素
1、复杂度总结
1、时间复杂度计算遵循的原则
1、复杂度与其具体的常系数无关(即:常数项的系数不要)
2、多项式级复杂度相加的时候,把其高项作为结果(即:多项式只保留最大项)
3、O(1)含义为:某个任务通过有限可数的资源即可完成
注:有限可数与输入的数据量n无关——常量复杂度
2、关于复杂度的经验性结论
1、一个顺序结构的代码,时间复杂度为O(1)——单纯的顺序或选择
2、采用分治法的二分策略,时间复杂度为O(log2 n) //log以2为底n的对数
3、一个简单的for循环,时间复杂度为O(n)
4、两个顺序执行的for循环,时间复杂度是取高项——并列的不累加
5、一般情况下,两层嵌套的for循环,时间复杂度为O(n²)
6、一般情况下,会使用递归,分治,动态规划等方法,用空间换取时间效率——时间宝贵、空间廉价
时间复杂度与代码结构有关,空间复杂度与数据结构有关
2、数据结构
数据结构分为线性结构和非线性结构,线性结构分为顺序存储和链式存储
线性结构:数组、链表、队列、栈、字符串
非线性结构:集合、树、图
数组和链表区别:
数组:空间连续、类型相同、长度固定的集合(顺序存储)
链表:增删快,但付出了查找的代价(链式存储)
| 数组 | 链表 | |||
| 是否连续 | 一定 | 不一定 | ||
| 大小 | 固定 | 不固定 | ||
| 查找 | 按照索引 | O(1) | O(n) | |
| 按照数值 | 有序 | 采用二分搜索 | ||
| 无序 | O(n) | |||
| 插入删除 | 头部 | O(n) | O(1) | |
| 中间 | O(n) | O(n) | ||
| 尾部 | O(1) | O(n) | ||
例题
存在一个含有n个元素的数组,数组内元素值均为0——n-1,检测数组内是否含有相同重复元素
解法
| 解法 | 时间复杂度 | 空间复杂度 |
| 1、暴力 | O(n**2) | O(1) |
| 2、容器 | O(n) | O(n) |
| 3、额外申请一个计数数组 | ||
| 4、排序后查看相邻数组元素值 | O(n*logn) | O(log2n) |
| 5、检测是否有没有出现的元素 | O(n**2) | O(1) |
| 6、sort+二分 | 更高 | O(n) |
| 7、在数组内部,将元素下标与元素值一一对应 | O(n) | O(1) |
1、按顺序把数组内每一个元素取出来,与后面每一个元素进行比较,如果有重复则报错
2、申请一个与原数组个数相同的数组,里面保存出现次数(2、3)
6、申请一个与原数组相同的数组,先将第一个元素放入数组内,接下来使用二分搜索法查找每个元素是否存在数组内
第七种方法代码
#include<iostream>bool check(int arr[],int length)
{int index = 0;for (int i = 0; i < length; i++){if (arr[index] == index){index++;}else{if (arr[arr[index]] == arr[index]){return false;}else{int t = arr[arr[index]];arr[arr[index]] = arr[index];arr[index] = t;}}}return true;
}int main()
{int arr[9] = { 1,2,8,4,3,5,0,7,6 };int length = sizeof(arr)/sizeof(int);if (check(arr, length)){printf("没有重复元素");}else{printf("有重复元素");}return 0;
}相关文章:

数据结构与算法——1122—复杂度总结检测相同元素
1、复杂度总结 1、时间复杂度计算遵循的原则 1、复杂度与其具体的常系数无关(即:常数项的系数不要) 2、多项式级复杂度相加的时候,把其高项作为结果(即:多项式只保留最大项) 3、O(1)含义为&…...

HTML通过JavaScript获取访问连接,IP和端口
<!DOCTYPE html> <html lang"en"> <head> <meta charset"UTF-8"> <title>Get IP Address</title> <script> function displayURL() { var url window.location.href; // 获取当…...

自动化测试过程操作细节
一、软件与框架介绍 1. Postman 读音:[pəʊstmən](剖斯特曼) 介绍:API开发与测试的得力助手,通过直观界面发送HTTP请求,查看响应数据。支持环境变量、集合、脚本等功能。 主要特点:易于使用…...

AR智能眼镜|AR眼镜定制开发|工业AR眼镜方案
AR眼镜的设计与制造成本主要受到芯片、显示屏和光学方案的影响,因此选择合适的芯片至关重要。一款优秀的芯片平台能够有效提升设备性能,并解决多种技术挑战。例如,采用联发科八核2.0GHz处理器,结合12nm制程工艺,这种低…...
从〇开始深度学习(0)——背景知识与环境配置
从〇开始深度学习(0)——背景知识与环境配置 文章目录 从〇开始深度学习(0)——背景知识与环境配置写在前面1.背景知识1.1.Pytorch1.2.Anaconda1.3.Pycharm1.4.CPU与GPU1.5.整体关系 2.环境配置2.1.准备工作2.1.1.判断有无英伟达显卡2.1.2.清理电脑里的旧环境 2.1.安装Anaconda…...
实验室管理技术革新:Spring Boot系统
4系统概要设计 4.1概述 本系统采用B/S结构(Browser/Server,浏览器/服务器结构)和基于Web服务两种模式,是一个适用于Internet环境下的模型结构。只要用户能连上Internet,便可以在任何时间、任何地点使用。系统工作原理图如图4-1所示: 图4-1系统工作原理…...
)
C语言 蓝桥杯某例题解决方案(查找完数)
蓝桥杯原题: 一个数如果恰好等于它的因子之和,这个数就称为“完数”。例如6 1 2 3.编程找出1000以内的所有完数。 这个题没有很大的难点,与我们上一个解决的问题“质因数分解”不同,它不需要判断因数是否是质数,因此…...
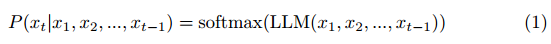
Prompting LLMs to Solve Complex Tasks: A Review
文章目录 题目简介任务分解未来方向结论 题目 促使 LLM 解决复杂任务: 综述 论文地址:https://www.intjit.org/cms/journal/volume/29/1/291_3.pdf 简介 大型语言模型 (LLM) 的最新趋势显而易见,这体现在大型科技公司的投资以及媒体和在线社…...

C++ 编程指南05 - 编译时检查优于运行时检查
一:概述 编译时错误检查是C编程中一条非常重要的原则,它强调了在可能的情况下,应该优先依赖编译时检查(静态检查)而不是运行时检查。这样做的主要目的是提高程序的性能、安全性和可维护性。 编译时检查,即在…...
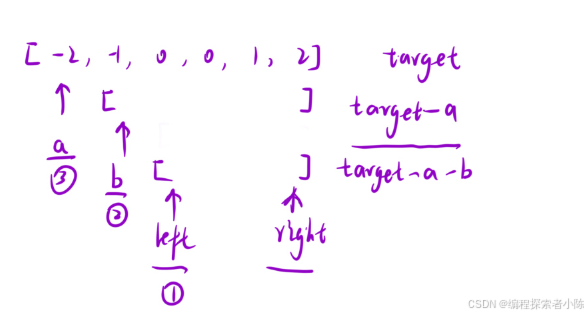
【优先算法】专题——双指针
1.移动零 移动零 题目描述: 思路: 本题我们把数组分块,将非零元素移动到左边,为零元素移动右边。 我们使用双指针算法(利用数组下标来充当指针) 两个指针的作用: cur:从左往右…...

CSP/信奥赛C++语法基础刷题训练(23):洛谷P1217:[USACO1.5] 回文质数 Prime Palindromes
CSP/信奥赛C语法基础刷题训练(23):洛谷P1217:[USACO1.5] 回文质数 Prime Palindromes 题目描述 因为 151 151 151 既是一个质数又是一个回文数(从左到右和从右到左是看一样的),所以 151 151 …...
C语言练习.if.else语句.strstr
今天在做题之前,先介绍一下,新学到的库函数strstr 想要使用它,要先给它一个头文件<string.h> char *strstr(const char*str1,const char*str2); 首先:1.strstr的返回值是char,字符类型的。 2.两个实参ÿ…...

利用浏览器录屏
以下内容参考自网络 <!DOCTYPE html> <html> <head> <meta charset"UTF-8"> <title></title> </head> <body> <div class"left"> <di…...

python中的map、split、join函数的作用 => ACM输入输出流
map(func,iter) lst_str ["1", "2", "3"] # 得到lst_num为[1, 2, 3] lst_num list(map(int, lst_str))如果想把一个列表里的所有元素批量地调用某一个函数,并映射得到一个新的列表(原列表中元素相对位置不变࿰…...
Ubuntu20.04下安装向日葵
向日葵远程控制app官方下载 - 贝锐向日葵官网 下载Ununtu版的图形版本的安装deb包SunloginClient_15.2.0.63064_amd64.deb 直接执行 sudo dpkg -i SunloginClient_15.2.0.63064_amd64.deb 的话会报错: 如果在Ubuntu20.04里直接执行sudo apt install libgconf-2-4安装libgco…...

常用并发设计模式
避免共享的设计模式 不变性(Immutability)模式,写时复制(Copy-on-Write)模式,线程本地存储(Thread-Specific Storage)模式本质上都是为了避免共享。 1、使用时需要注意不变性模式…...
Redis Search系列 - 第七讲 Windows(CygWin)编译Friso
目录 一、背景二、安装CygWin三、编译Friso四、运行Friso五、Friso分词效果测试 一、背景 最近在做RedisSearch的中文分词效果调研,底层的中文分词插件使用的就是Friso,目前手里的Linux环境上yum镜像仓库有问题导致没法安装gcc,又急于验证Fr…...
利用Docker容器技术部署发布web应用程序
Docker是什么? docker 是一个开源的应用容器引擎,可以帮助开发者打包应用以及依赖包到一个可移植的容器中,然后发布到任何流行的Linux机器上,也可以实现虚拟化,容器是完全使用沙箱机制,相互之间不会有任何…...

[免费]SpringBoot+Vue毕业设计论文管理系统【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的SpringBootVue毕业设计论文管理系统,分享下哈。 项目视频演示 【免费】SpringBootVue毕业设计论文管理系统 Java毕业设计_哔哩哔哩_bilibili 项目介绍 现代经济快节奏发展以及不断完善升级的信…...

BFS 算法专题(五):BFS 解决拓扑排序
目录 1. 拓扑排序简介 1.1 有向无环图 (DAG 图) 1.2 AOV 网(顶点活动图) 1.3 拓扑排序 1.3.1 如何实现 2. 力扣实战应用 2.1 课程表 2.1.1 算法原理 2.1.2 算法代码 2.2 课程表 II 2.2.1 算法原理 2.2.2 算法代码 2.3 火星词典 (hard) (原剑指offer) 2.3.1 算法原理…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...
