BFS 算法专题(五):BFS 解决拓扑排序
目录
1. 拓扑排序简介
1.1 有向无环图 (DAG 图)
1.2 AOV 网(顶点活动图)
1.3 拓扑排序
1.3.1 如何实现
2. 力扣实战应用
2.1 课程表
2.1.1 算法原理
2.1.2 算法代码
2.2 课程表 II
2.2.1 算法原理
2.2.2 算法代码
2.3 火星词典 (hard) (原剑指offer)
2.3.1 算法原理
2.3.2 算法代码
1. 拓扑排序简介
1.1 有向无环图 (DAG 图)
顶点与顶点之间的边, 是具有方向, 并且不会构成环(无回路).
有向图中, 有两个重要概念:
- 出度
- 入度
1.2 AOV 网(顶点活动图)
在有向无环图中, 用顶点来表示一个活动, 用边来表示活动的先后顺序的图结构.

1.3 拓扑排序
找到做的事情(活动)的先后顺序(可能不是唯一的).
排序过程:
- 找到入度为 1 的点
- 删除与该点连接的边
- 重复 1, 2 操作, 直至图中没有点或者没有入度为 0 的点(可能存在环)
重要应用: 判断有向图中是否有环
1.3.1 如何实现
借助队列, 进行一次 BFS:
初始化: 把所有入度为 0 的点加入到队列中
当队列不为空时:
- 拿出队头元素, 加入已排序序列
- 删除与该元素相连接的边
- 判断: 与删除边相连的点, 是否入度为 0 , 若是, 则加入队列中
2. 力扣实战应用
2.1 课程表
. - 力扣(LeetCode)
2.1.1 算法原理
问题核心: 判断 "图" 中是否带环 => 拓扑排序
灵活使用 Java 提供的集合类, 进行图的构建:
- 构建邻接表 => 1. List<List<Integer>> 2. Map<Integer, List<Integer>>
借助队列, 进行 BFS , 判断是否带环:
- 将所有入度为 0 的节点入队(从图中拿走该节点)
- 拿出队头元素, 删除与该元素相邻的边
- 判断与删除的边相连的节点入度是否为 0
- 若为 0 , 则入队
- 重复以上操作
- 当队空时, 若还有入度不为 0 的节点, 则说明该图带环
注意: 使用数组记录各节点的入度 => int[] in

2.1.2 算法代码
class Solution {public boolean canFinish(int n, int[][] p) {// 记录节点的入度int[] in = new int[n];// 构建邻接表Map<Integer, List<Integer>> edges = new HashMap<>();for(int i = 0; i < p.length; i++) {int a = p[i][0], b = p[i][1]; // b -> aif(!edges.containsKey(b)) {edges.put(b, new ArrayList<>());}edges.get(b).add(a);in[a]++;}Queue<Integer> q = new LinkedList<>();// 将入度为 0 的节点入队for(int i = 0; i < n; i++) {if(in[i] == 0) q.offer(i);}// bfswhile(!q.isEmpty()) {int t = q.poll();for(int x : edges.getOrDefault(t, new ArrayList<>())) {in[x]--;if(in[x] == 0) q.offer(x);}}for(int x : in) {if(x != 0) return false;}return true;}
}2.2 课程表 II
. - 力扣(LeetCode)
2.2.1 算法原理
本题解法与上题解法一致, 唯一需要多处理的就是记录拓扑排序的序列.
2.2.2 算法代码
class Solution {public int[] findOrder(int n, int[][] p) {// 统计节点的入度情况int[] in = new int[n + 1];// 创建邻接表Map<Integer, List<Integer>> edges = new HashMap<>();for(int i = 0; i < p.length; i++) {int a = p[i][0], b = p[i][1]; // b -> ain[a]++;if(!edges.containsKey(b)) {edges.put(b, new ArrayList<>());}edges.get(b).add(a);}Queue<Integer> q = new LinkedList<>();// 将入度为 0 的节点入队for(int i = 0; i < n; i++) {if(in[i] == 0) q.offer(i);}int size = 0;int[] ret = new int[n];// bfswhile(!q.isEmpty()) {int t = q.poll();// 进入拓扑序列ret[size++] = t;for(int x : edges.getOrDefault(t, new ArrayList<>())) {in[x]--;if(in[x] == 0) q.offer(x);}}return size == n ? ret : new int[]{};}
}2.3 火星词典 (hard) (原剑指offer)
. - 力扣(LeetCode)
2.3.1 算法原理
-
统计节点的入度信息 => Map<Character, Integer> ; 将每个节点的入度信息初始化为 0
-
构建邻接表 => Map<Character, Set<Character>> ; 注意不能重复接入存在的元素(所以使用 HashSet, 查找速度快)
-
搜集顺序信息 => 两层 for 循环 + 前后指针
-
细节问题 => "abc" "ab" , 这种特殊情况不合法, return "";
2.3.2 算法代码
class Solution {public String alienOrder(String[] words) {// 统计每个字符的入度Map<Character, Integer> in = new HashMap<>();for(String s : words) {for(int i = 0; i < s.length(); i++) {char ch = s.charAt(i);if(!in.containsKey(ch)) in.put(ch, 0);}}// 构建邻接表Map<Character, Set<Character>> edges = new HashMap<>();for(int i = 0; i < words.length; i++) {for(int j = i + 1; j < words.length; j++) {int front = 0, tail = 0;String s1 = words[i], s2 = words[j];while(front < s1.length() && tail < s2.length()) {char ch1 = s1.charAt(front), ch2 = s2.charAt(tail);if(ch1 == ch2) {front++;tail++;}else {// ch1 -> ch2// 可能重复存在 : ch1 -> ch2if(edges.containsKey(ch1) && edges.get(ch1).contains(ch2)) {break;} if(!edges.containsKey(ch1)) {edges.put(ch1, new HashSet<>());}// 入度加一in.put(ch2, in.get(ch2) + 1);// 放入邻接表edges.get(ch1).add(ch2);break;}}// 字符串不合法if(front < s1.length() && tail >= s2.length()) return ""; }}Queue<Character> q = new LinkedList<>();StringBuilder stringBuilder = new StringBuilder();// 将入度为 0 的节点入队for(Map.Entry<Character, Integer> e : in.entrySet()) {if(e.getValue() == 0) q.offer(e.getKey());}// bfswhile(!q.isEmpty()) {char ch = q.poll();stringBuilder.append(ch);Set<Character> set = edges.getOrDefault(ch, new HashSet<>());for(Character x : set) {in.put(x, in.get(x) - 1);if(in.get(x) == 0) q.offer(x);}}for(Map.Entry<Character, Integer> e : in.entrySet()) {if(e.getValue() != 0) return "";}return stringBuilder.toString();}
}END
相关文章:

BFS 算法专题(五):BFS 解决拓扑排序
目录 1. 拓扑排序简介 1.1 有向无环图 (DAG 图) 1.2 AOV 网(顶点活动图) 1.3 拓扑排序 1.3.1 如何实现 2. 力扣实战应用 2.1 课程表 2.1.1 算法原理 2.1.2 算法代码 2.2 课程表 II 2.2.1 算法原理 2.2.2 算法代码 2.3 火星词典 (hard) (原剑指offer) 2.3.1 算法原理…...
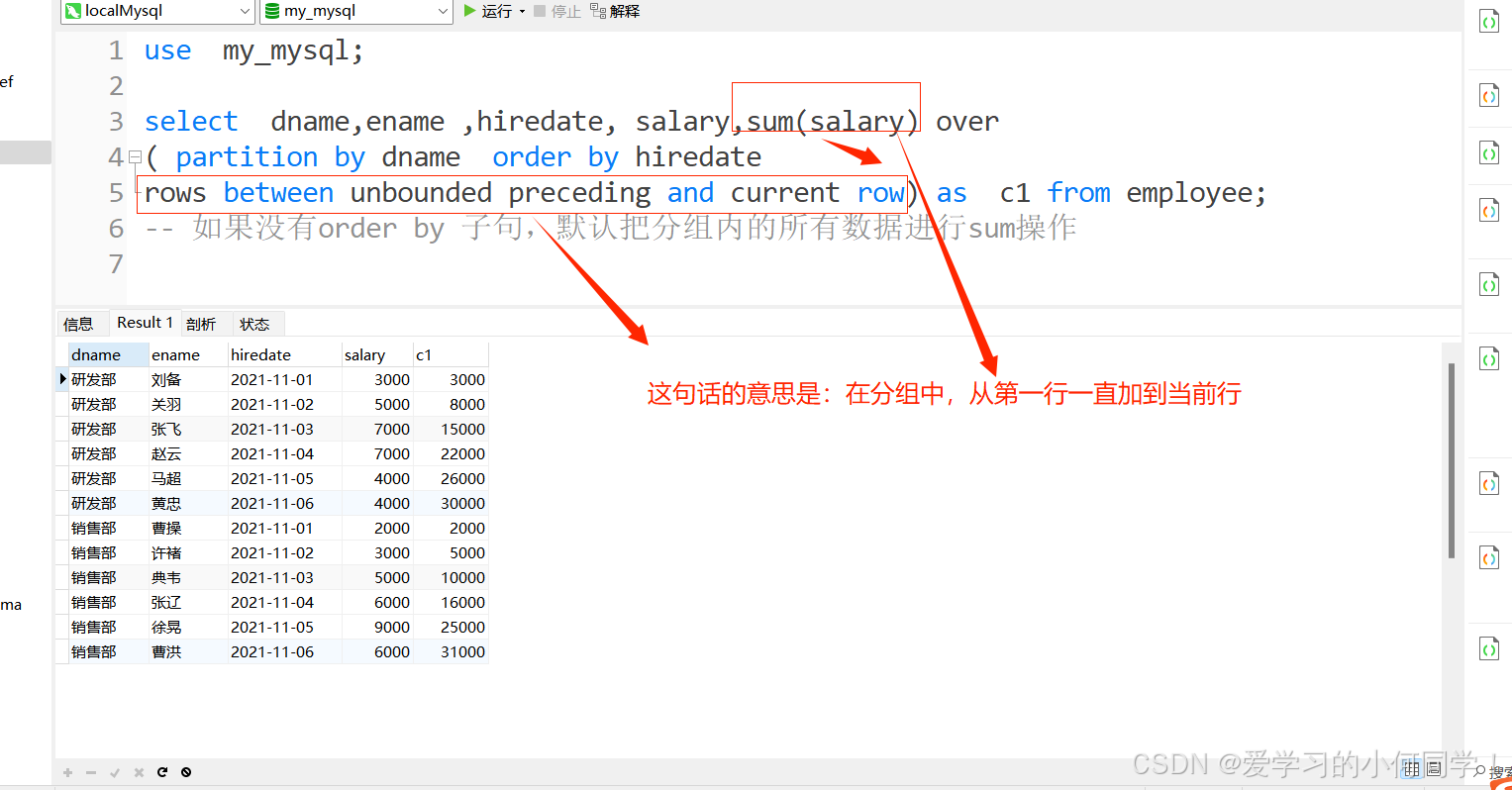
【Mysql】开窗聚合函数----SUM,AVG, MIN,MAX
1、概念 在窗口中,每条记录动态地应用聚合函数(如:SUM(),AVG(),MAX(),MIN(),COUNT(),)可以动态计算在指定的窗口内的各种聚合函数值。 2、操作 以下操作将基于employee表进行操作。 sum() 进行sum的时候,没有order …...

java操作doc——java利用Aspose.Words操作Word文档并动态设置单元格合并
在实际工作中,如果业务线是管理类项目或者存在大量报表需要导出的业务时,可以借助第三方插件实现其对应功能。 尤其是需要对word文档的动态操作或者模板数据的定向合并,使用Aspose会相对来说容易一些,而且相关文档比较完整&#…...
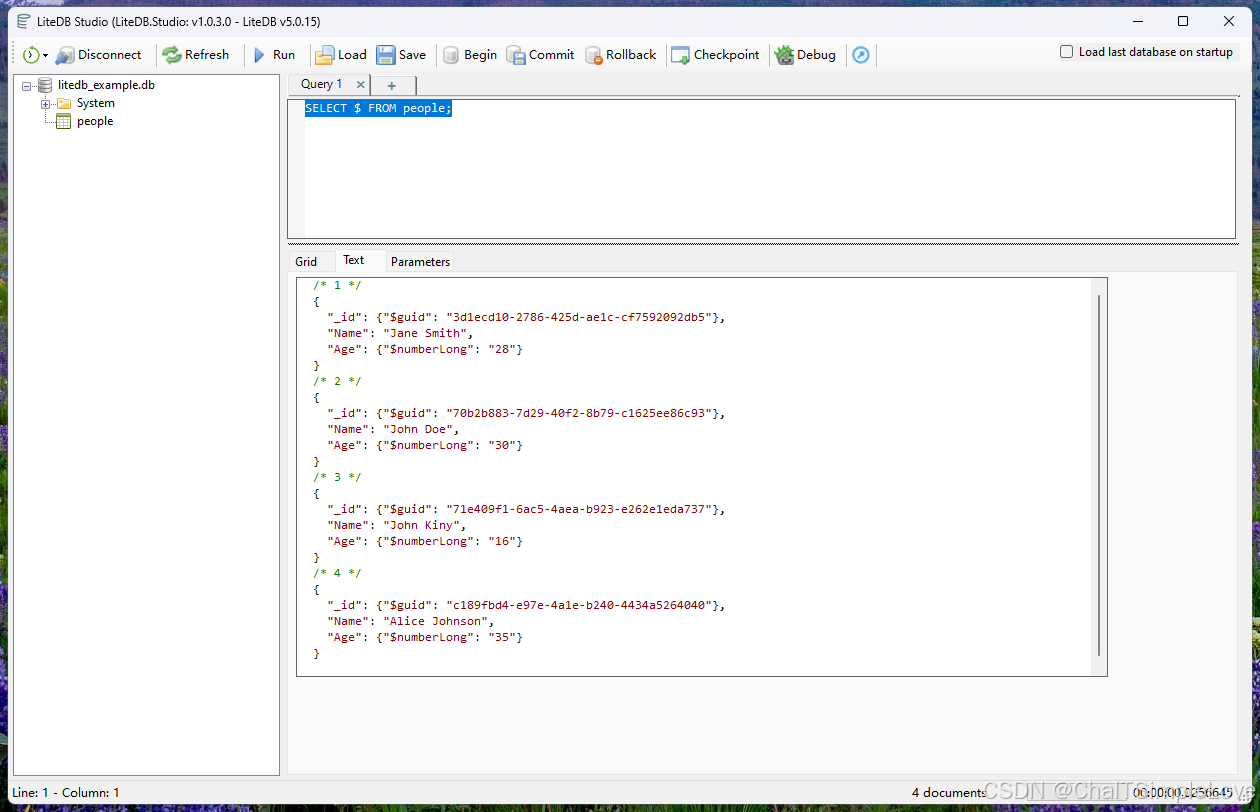
探索 .NET 9 控制台应用中的 LiteDB 异步 CRUD 操作
本文主要是使用异步方式,体验 litedb 基本的 crud 操作。 LiteDB 是一款轻量级、快速且免费的 .NET NoSQL 嵌入式数据库,专为小型本地应用程序设计。它以单一数据文件的形式提供服务,支持文档存储和查询功能,适用于桌面应用、移动…...

《进程隔离机制:C++多进程编程安全的坚固堡垒》
在当今数字化时代,软件系统的安全性愈发成为人们关注的焦点。尤其是在 C多进程编程领域,如何确保进程间的安全交互与数据保护,是每一位开发者都必须面对的重要课题。而进程隔离机制,犹如一座坚固的堡垒,为 C多进程编程…...

构建无障碍的数字世界:深入探讨Web可访问性指南
文章目录 前言一、什么是Web可访问性?二、Web内容无障碍指南(WCAG)三、ARIA属性的应用四、实践中的Web可访问性结语 前言 在当今高度互联的世界里,互联网已成为人们日常生活不可或缺的一部分。然而,对于数百万残障人士…...

跨境出海安全:如何防止PayPal账户被风控?
今天咱们聊聊那些让人头疼的事儿——PayPal账户被风控。不少跨境电商商家反馈,我们只是想要安安静静地在网上做个小生意,结果不知道为什么,莫名其妙账户就被冻结了。 但其实每个封禁都是有原因的,今天就来给大家分享分享可能的原…...

学习日记_20241123_聚类方法(MeanShift)
前言 提醒: 文章内容为方便作者自己后日复习与查阅而进行的书写与发布,其中引用内容都会使用链接表明出处(如有侵权问题,请及时联系)。 其中内容多为一次书写,缺少检查与订正,如有问题或其他拓展…...

AI编程和AI绘画哪个更适合创业?
AI编程和AI绘画各有优势,适合创业的方向取决于你的资源、兴趣、市场需求和技术能力。以下是两者的对比分析,帮助你选择更适合的方向: AI编程 优势 1、广泛应用领域: 涉及自动化、数据分析、自然语言处理、计算机视觉等多个领域&a…...

macOS 无法安装第三方app,启用任何来源的方法
升级新版本 MacOS 后,安装下载的软件时,不能在 ”安全性与隐私” 中找不到 ”任何来源” 选项。 1. 允许展示任何来源 点击 启动器 (Launchpad) – 其他 (Other) – 终端 (Terminal): 打开终端后,输入以下代码回车: …...

关于SpringBoot集成Kafka
关于Kafka Apache Kafka 是一个分布式流处理平台,广泛用于构建实时数据管道和流应用。它能够处理大量的数据流,具有高吞吐量、可持久化存储、容错性和扩展性等特性。 Kafka一般用作实时数据流处理、消息队列、事件架构驱动等 Kafka的整体架构 ZooKeeper:…...

4.STM32之通信接口《精讲》之IIC通信---软件实现IIC《深入浅出》面试必备!
接下正式,进入软件编写IIC时序了,并实现对MPU6050的控制,既然是软件实现,那么硬件方面,我仅需两根控制线即可,即:数据控制线SDA,时钟控制线SCL。(人为软件层面定义的&…...

6G通信技术对比5G有哪些不同?
6G,即第六代移动通信技术,是5G之后的延伸,代表了一种全新的通信技术发展方向。与5G相比,6G在多个方面都有显著的不同和提升,以下是对6G通信技术及其与5G差异的详细分析: 一、6G的基本特点 更高的传输速率…...

「Mac玩转仓颉内测版28」基础篇8 - 元组类型详解
本篇将介绍 Cangjie 中的元组类型,包括元组的定义、创建、访问、数据解构以及应用场景,帮助开发者掌握元组类型的使用。 关键词 元组类型定义元组创建元组访问数据解构应用场景 一、元组类型概述 在 Cangjie 中,元组是一种用于存储多种数据…...

WebStorm 2024.3/IntelliJ IDEA 2024.3出现elementUI提示未知 HTML 标记、组件引用爆红等问题处理
WebStorm 2024.3/IntelliJ IDEA 2024.3出现elementUI提示未知 HTML 标记、组件引用爆红等问题处理 1. 标题识别elementUI组件爆红 这个原因是: 在官网说明里,才版本2024.1开始,默认启用的 Vue Language Server,但是在 Vue 2 项目…...

机械设计学习资料
免费送大家学习资源,已整理好,仅供学习 下载网址: https://www.zzhlszk.com/?qZ02-%E6%9C%BA%E6%A2%B0%E8%AE%BE%E8%AE%A1%E8%A7%84%E8%8C%83SOP.zip...

Python 快速入门(上篇)❖ Python 字符串
Python 字符串 字符串格式化输出字符串拼接获取字符串长度字符串切片字符串处理方法 字符串格式化输出 name “xhx” age 30 # 方法1 print("我的名字是%s,今年%s岁了。 " % (name, age)) # 方法2 print(f"我的名字是{name},今年{age}岁了。")字符串拼接…...

Ubuntu中使用多版本的GCC
我的系统中已经安装了GCC11.4,在安装cuda时出现以下错误提示: 意思是当前的GCC版本过高,要在保留GCC11.4的同时安装GCC9并可以切换,可以通过以下步骤实现: 步骤 1: 安装 GCC 9 sudo apt-get update sudo apt-get ins…...

1+X应急响应(网络)文件包含漏洞:
常见网络攻击-文件包含漏洞&命令执行漏洞: 文件包含漏洞简介: 分析漏洞产生的原因: 四个函数: 产生漏洞的原因: 漏洞利用条件: 文件包含: 漏洞分类: 本地文件包含: …...
)
机器学习实战记录(1)
决策树——划分数据集 def splitDataSet(dataSet, axis, value): retDataSet [] #创建返回的数据集列表for featVec in dataSet: #遍历数据集if featVec[axis] value:reducedFeatVec featVec[:axis] #去掉axis特征reducedFeatVec.extend(featVec[axis1…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...
