当前位置：首页 > news >正文

因果机器学习EconML | 客户细分案例——基于机器学习的异质性处理效果估计

news 2025/7/8 14:54:49

机器学习的最大承诺之一是在众多应用领域中实现决策自动化。在大多数数据驱动的个性化决策场景中出现的一个核心问题是对异质性处理效果的估计：作为处理样本的一组可观察特征的函数，干预对感兴趣结果的影响是什么？例如，这个问题出现在个性化定价中，其目标是根据消费者的特征来估计价格折扣对需求的影响。同样，它出现在医学试验中，其目标是根据患者特征估计药物治疗对患者临床反应的影响。在许多此类环境中，我们有大量的观察数据，其中处理是通过一些未知的策略选择的，并且运行 A/B 测试的能力是有限的。

EconML 软件包在计量经济学和机器学习的交叉点实施了文献中的最新技术，这些技术通过基于机器学习的方法解决了异构治疗效果估计的问题。这些新方法在模拟效应异质性方面提供了很大的灵活性（通过随机森林、提升、套索和神经网络等技术），同时利用因果推理和计量经济学的技术来保留对学习模型的因果解释，并且很多时候还通过构建有效的置信区间提供统计有效性。

客户细分：基于机器学习的异质性处理效果估计

背景

媒体订阅服务希望通过个性化定价计划提供有针对性的折扣。

问题

他们观察了客户的许多特征，但不确定哪些客户对较低的价格反应最强烈。

解决方案

EconML 的 DML 估算器使用现有数据中的价格变化以及一组丰富的用户特征来估计随多个客户特征而变化的异构价格敏感性。树解释器提供了关键功能的演示就绪摘要，这些功能解释了对折扣的响应能力的最大差异。

如今，业务决策者依靠估计干预措施的因果效应来回答有关战略转变的假设问题，例如以折扣促销特定产品、向网站添加新功能或增加销售团队的投资。然而，人们越来越感兴趣的是了解不同用户对这两种选择的不同反应，而不是了解是否为所有用户采取特定干预。确定对干预反应最强烈的用户的特征有助于制定规则，将未来的用户划分为不同的组。这有助于优化策略以使用最少的资源并获得最大的利润。

在本案例研究中，我们将使用个性化定价示例来解释 EconML 和 DoWhy 库如何适应这个问题并提供强大而可靠的因果解决方案。

背景

多年来，全球在线媒体市场正在快速增长。媒体公司总是有兴趣吸引更多用户进入市场并鼓励他们购买更多歌曲或成为会员。在此示例中，我们将考虑这样一个场景：一家媒体公司正在进行的一项实验是根据其当前用户的收入水平为其当前用户提供小额折扣（10%、20% 或 0），以提高他们购买的可能性。目标是了解不同收入水平的人的需求的异质价格弹性，了解哪些用户对小额折扣的反应最强烈。此外，他们的最终目标是确保在降低一些消费者的价格的同时，需求得到足够的提高以提高整体收入。

EconML 和 DoWhy 库在实施此解决方案时相辅相成。一方面，DoWhy 库可以帮助构建因果模型，识别因果效应并测试因果假设。另一方面，EconML 基于 DML 的估算器可用于获取现有数据中的折扣变化以及一组丰富的用户特征，以估计随多个客户特征而变化的异构价格敏感性。然后，SingleTreeCateInterpreter 提供了关键功能的演示就绪摘要，这些功能解释了对折扣的响应能力的最大差异，SingleTreePolicyInterpreter 建议了一个关于谁应该获得折扣以增加收入（不仅仅是需求）的策略，这可以帮助公司在未来为这些用户设置最佳价格。

``# Some imports to get us started
# Utilities
import numpy as np
import pandas as pd
from networkx.drawing.nx_pydot import to_pydot
from IPython.display import Image, display
# Generic ML imports
from sklearn.preprocessing import PolynomialFeatures
from sklearn.ensemble import GradientBoostingRegressor
# EconML imports
from econml.dml import LinearDML, CausalForestDML
from econml.cate_interpreter import SingleTreeCateInterpreter, SingleTreePolicyInterpreter
import matplotlib.pyplot as plt
import warnings
warnings.simplefilter('ignore')
%matplotlib inline

数据

该数据集*有 ~10,000 个观察结果，包括 9 个连续和分类变量，代表用户的特征和在线行为历史，例如年龄、日志收入、以前的购买、每周以前的在线时间等。

我们定义以下变量：

Feature Name	Type	Details
account_age	W	user’s account age
age	W	user’s age
avg_hours	W	the average hours user was online per week in the past
days_visited	W	the average number of days user visited the website per week in the past
friend_count	W	number of friends user connected in the account
has_membership	W	whether the user had membership
is_US	W	whether the user accesses the website from the US
songs_purchased	W	the average songs user purchased per week in the past
income	X	user’s income
price	T	the price user was exposed during the discount season (baseline price * small discount)
demand	Y	songs user purchased during the discount season

为了保护公司隐私，我们这里以模拟数据为例。数据是综合生成的，特征分布与真实分布不对应。然而，功能名称保留了它们的名称和含义。

处理和结果是使用以下函数生成的：

$\begin{cases} 1 & \text{with } p=0.2, \\ 0.9 & \text{with } p=0.3, & \text{if income} < 1 \\ 0.8 & \text{with } p=0.5, \\ \\ 1 & \text{with } p=0.7, \\ 0.9 & \text{with } p=0.2, & \text{if income} \geq 1 \\ 0.8 & \text{with } p=0.1, \\ \end{cases}$

$\begin{align} \gamma(X) & = -3 - 14 \cdot \{\text{income} < 1\} \end{align}$

$KaTeX parse error: Expected 'EOF', got '_' at position 54: …\cdot \text{avg_̲hours} + 5 \cdo…$
$\begin{align} Y = \gamma(X) \cdot T + \beta(X, W) \end{align}$

# 导入样本定价数据
file_url = "https://msalicedatapublic.z5.web.core.windows.net/datasets/Pricing/pricing_sample.csv"
train_data = pd.read_csv(file_url)

# 定义估计器输入
train_data["log_demand"] = np.log(train_data["demand"])
train_data["log_price"] = np.log(train_data["price"])Y = train_data["log_demand"].values
T = train_data["log_price"].values
X = train_data[["income"]].values  # features
confounder_names = ["account_age", "age", "avg_hours", "days_visited", "friends_count", "has_membership","is_US", "songs_purchased"]
W = train_data[confounder_names].values

# 获取测试数据
X_test = np.linspace(0, 5, 100).reshape(-1, 1)
X_test_data = pd.DataFrame(X_test, columns=["income"])

利用 DoWhy 创建因果模型并确定因果效应

我们用 DoWhy 来定义因果假设。例如，我们可以将我们认为是混杂因素的特征和我们认为会影响效应异质性的特征包括在内。定义了这些假设后，DoWhy 就能为我们生成因果图，并利用该图首先确定因果效应。

# 启动 EconML 类别估计器
est = LinearDML(model_y=GradientBoostingRegressor(), model_t=GradientBoostingRegressor(),featurizer=PolynomialFeatures(degree=2, include_bias=False))
# 通过 dowhy 进行拟合
est_dw = est.dowhy.fit(Y, T, X=X, W=W,outcome_names=["log_demand"], treatment_names=["log_price"], feature_names=["income"],confounder_names=confounder_names, inference="statsmodels")
# 可视化因果图
try:# 尝试漂亮地打印图表。需要 pydot 和 pygraphvizdisplay(Image(to_pydot(est_dw._graph._graph).create_png()))
except Exception:# 回到默认的图表视图est_dw.view_model(layout=None)

identified_estimand = est_dw.identified_estimand_
print(identified_estimand)

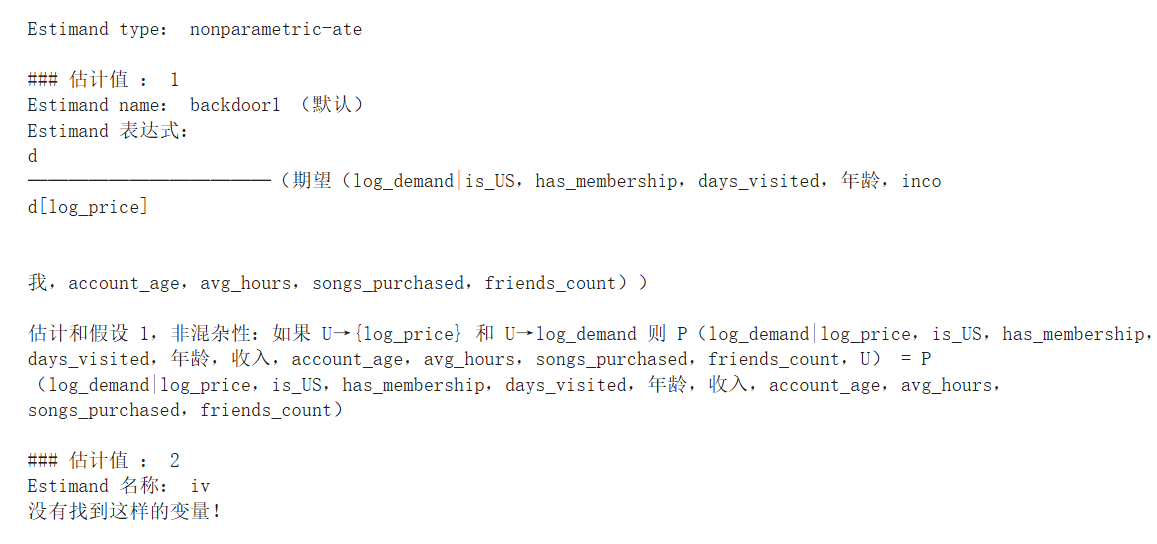
使用 EconML 获取因果效应

基于上面确定的因果效应，我们使用 EconML 按如下方式拟合模型：

$\begin{align} log(Y) & = \theta(X) \cdot log(T) + f(X,W) + \epsilon \\ log(T) & = g(X,W) + \eta \end{align}$

其中 $\epsilon, \eta$ 是不相关的误差项。

我们在这里拟合的模型与上述数据生成函数并不完全匹配，但如果它们是一个良好的近似，就可以帮助我们制定一个有效的折扣策略。尽管模型存在误设定问题，我们仍希望看到基于 DML 的估计器能够捕捉到 $\theta(X)$ 的正确趋势，并且推荐的策略在收入方面能优于其他基线策略（例如始终提供折扣）。由于数据生成过程和我们拟合的模型之间存在不匹配，实际上不存在唯一真实的 $\theta(X)$ （真实的弹性不仅与 X 有关，还与 T 和 W 相关）。然而，根据上述数据生成过程，我们仍然可以计算真实 $\theta(X)$ 的范围用于比较。

# 定义给定 DGP 的基础处理效果函数
def gamma_fn(X):return -3 - 14 * (X["income"] < 1)def beta_fn(X):return 20 + 0.5 * (X["avg_hours"]) + 5 * (X["days_visited"] > 4)def demand_fn(data, T):Y = gamma_fn(data) * T + beta_fn(data)return Ydef true_te(x, n, stats):if x < 1:subdata = train_data[train_data["income"] < 1].sample(n=n, replace=True)else:subdata = train_data[train_data["income"] >= 1].sample(n=n, replace=True)te_array = subdata["price"] * gamma_fn(subdata) / (subdata["demand"])if stats == "mean":return np.mean(te_array)elif stats == "median":return np.median(te_array)elif isinstance(stats, int):return np.percentile(te_array, stats)

# 得到真实处理效果的估计值和范围
truth_te_estimate = np.apply_along_axis(true_te, 1, X_test, 1000, "mean")  # estimate
truth_te_upper = np.apply_along_axis(true_te, 1, X_test, 1000, 95)  # upper level
truth_te_lower = np.apply_along_axis(true_te, 1, X_test, 1000, 5)  # lower level

参数异质性

首先，我们可以尝试在假设 $\theta(X)$ 为多项式形式的情况下，学习处理效应的线性投影。为此，我们使用了 LinearDML 估计器。由于我们对这些模型没有任何先验假设，我们使用通用的梯度提升树估计器从数据中学习预期的价格和需求。

lineardml_estimate = est_dw.estimate_
print(lineardml_estimate)

# 获取处理效果及其置信区间
te_pred = est_dw.effect(X_test).flatten()
te_pred_interval = est_dw.effect_interval(X_test)

# 比较估计值和真实值
plt.figure(figsize=(10, 6))
plt.plot(X_test.flatten(), te_pred, label="Sales Elasticity Prediction")
plt.plot(X_test.flatten(), truth_te_estimate, "--", label="True Elasticity")
plt.fill_between(X_test.flatten(),te_pred_interval[0].flatten(),te_pred_interval[1].flatten(),alpha=0.2,label="95% Confidence Interval",
)
plt.fill_between(X_test.flatten(),truth_te_lower,truth_te_upper,alpha=0.2,label="True Elasticity Range",
)
plt.xlabel("Income")
plt.ylabel("Songs Sales Elasticity")
plt.title("Songs Sales Elasticity vs Income")
plt.legend(loc="lower right")

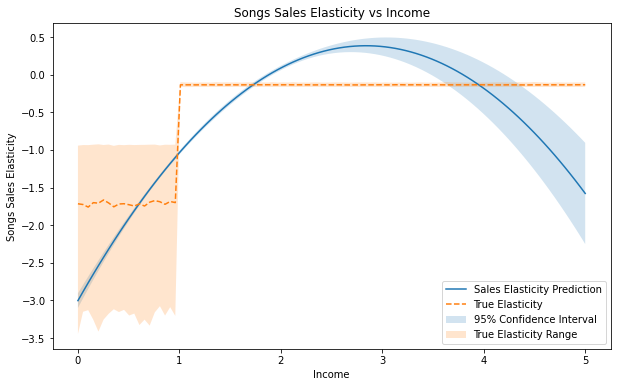
从上图可以清楚地看出，真正的处理效果是收入的非线性函数，当收入小于 1 时弹性约为 -1.75，当收入大于 1 时，弹性较小。该模型拟合二次处理效应，这不是一个很好的拟合。但它仍然抓住了总体趋势：弹性是负的，如果人们的收入更高，他们对价格变化的敏感度就会降低。

# 得到最终的系数和截距总结
est_dw.summary(feature_names=["income"])

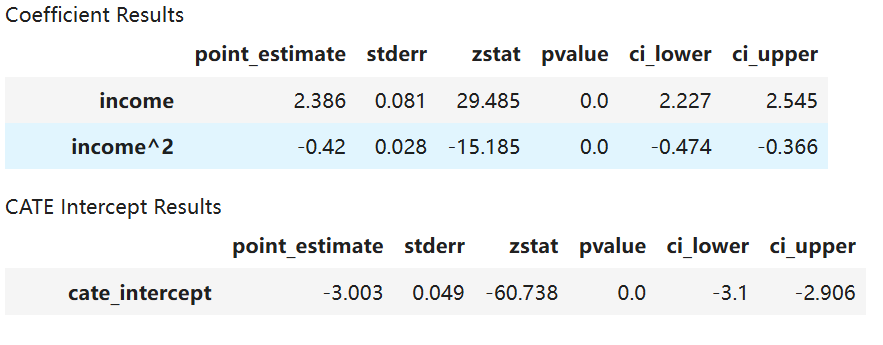
LinearDML 估计器还可以返回最终模型的系数和截距的摘要，其中包括点估计、p 值以及置信区间。从上表可以看出， $in co m e$ 对结果具有正向影响，而 ${income}^2$ 则具有负向影响，且这两者均在统计上显著。

非参数异质性

既然我们已经知道真正的处理效应函数是非线性的，那么让我们使用 CausalForestDML 拟合另一个模型，该模型假设处理效应的完全非参数估计。

# 启动 EconML 类别估计器
est_nonparam = CausalForestDML(model_y=GradientBoostingRegressor(), model_t=GradientBoostingRegressor())
# 通过 dowhy 进行拟合
est_nonparam_dw = est_nonparam.dowhy.fit(Y, T, X=X, W=W, outcome_names=["log_demand"], treatment_names=["log_price"],feature_names=["income"], confounder_names=confounder_names, inference="blb")
# 获取处理效果及其置信区间
te_pred = est_nonparam_dw.effect(X_test).flatten()
te_pred_interval = est_nonparam_dw.effect_interval(X_test)

# 比较估计值和真实值
plt.figure(figsize=(10, 6))
plt.plot(X_test.flatten(), te_pred, label="Sales Elasticity Prediction")
plt.plot(X_test.flatten(), truth_te_estimate, "--", label="True Elasticity")
plt.fill_between(X_test.flatten(),te_pred_interval[0].flatten(),te_pred_interval[1].flatten(),alpha=0.2,label="95% Confidence Interval",
)
plt.fill_between(X_test.flatten(),truth_te_lower,truth_te_upper,alpha=0.2,label="True Elasticity Range",
)
plt.xlabel("Income")
plt.ylabel("Songs Sales Elasticity")
plt.title("Songs Sales Elasticity vs Income")
plt.legend(loc="lower right")

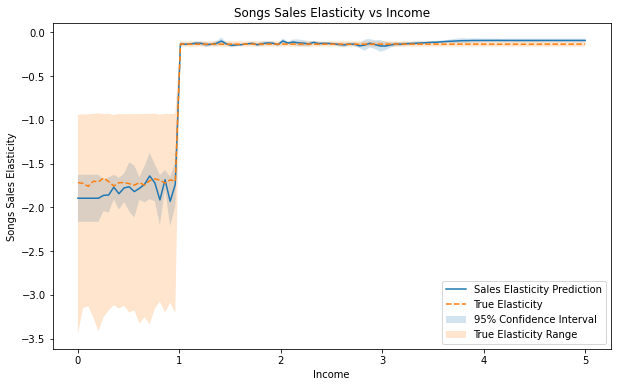
我们注意到该模型比 LinearDML 拟合得更好，95% 置信区间正确地涵盖了真实的处理效果估计值，并捕获了收入约为 1 时的变化。总体而言，该模型显示，低收入人群比高收入人群对价格变化更敏感。

使用 DoWhy 检验估计稳健性

添加随机常见原因

我们的估计值对增加另一个混杂因素有多稳健？我们使用 DoWhy 来测试这个！

res_random = est_nonparam_dw.refute_estimate(method_name="random_common_cause", num_simulations=5)
print(res_random)

添加未观察到的常见原因

我们对未观察到的混杂因素的估计有多稳健？由于我们假设模型处于非混杂性下，因此添加未观察到的混杂因素可能会使估计值产生偏差。我们使用 DoWhy 来测试这个！

res_unobserved = est_nonparam_dw.refute_estimate(method_name="add_unobserved_common_cause",confounders_effect_on_treatment="linear",confounders_effect_on_outcome="linear",effect_strength_on_treatment=0.1,effect_strength_on_outcome=0.1,
)
print(res_unobserved)

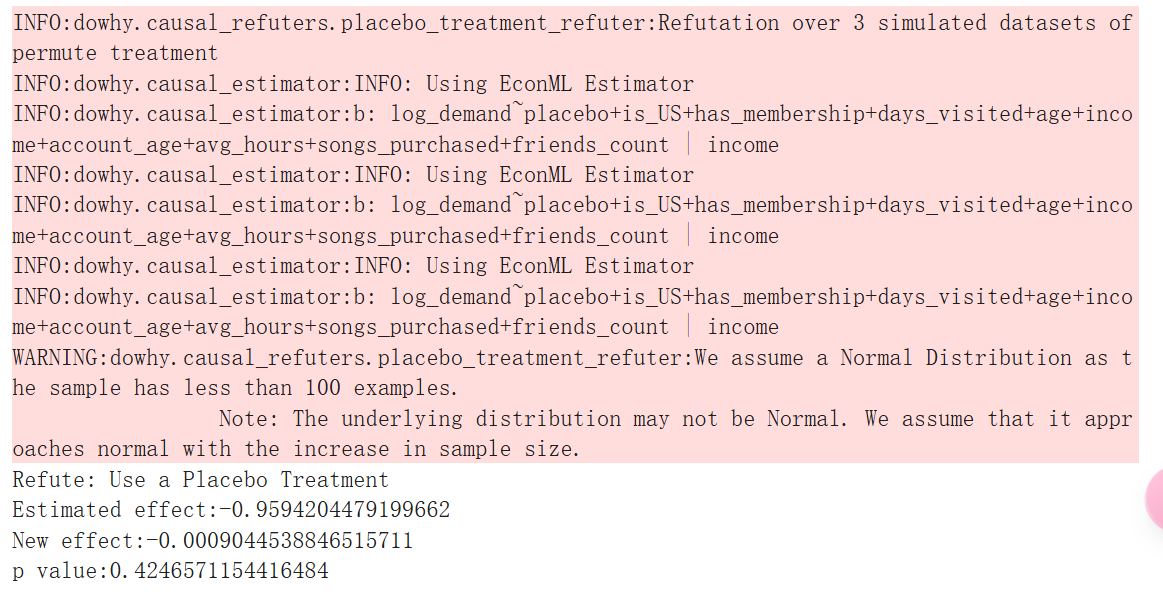
用随机（安慰剂）变量替换处理

如果我们用噪声替换处理变量，我们的估计值会发生什么变化？理想情况下，平均效果将与我们最初的估计大相径庭。我们使用 DoWhy 来调查！

res_placebo = est_nonparam_dw.refute_estimate(method_name="placebo_treatment_refuter", placebo_type="permute",num_simulations=3
)
print(res_placebo)

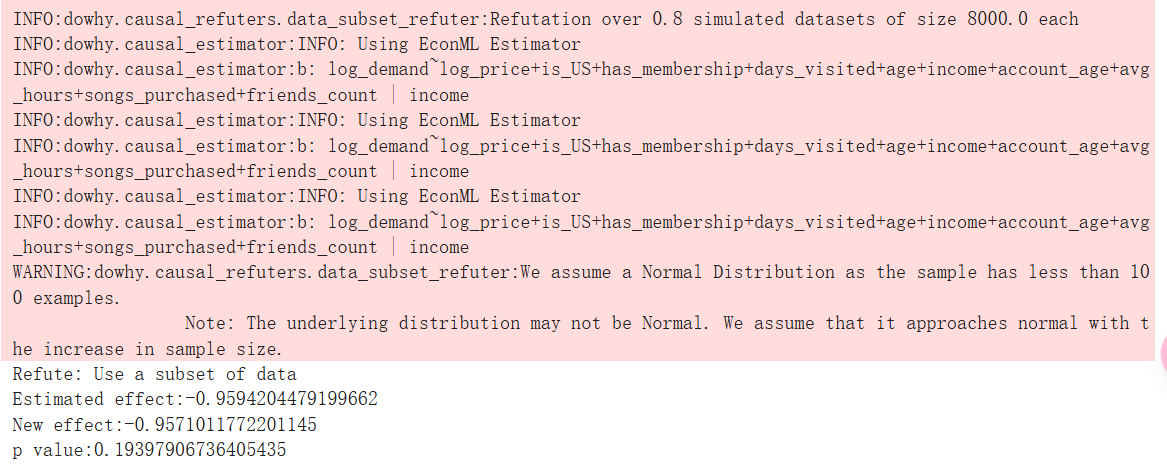
删除数据的随机子集

我们是否可以恢复数据子集的类似估计值？这说明了我们选择的估计器能够很好地泛化。我们使用 DoWhy 来调查这个问题！

res_subset = est_nonparam_dw.refute_estimate(method_name="data_subset_refuter", subset_fraction=0.8,num_simulations=3)
print(res_subset)

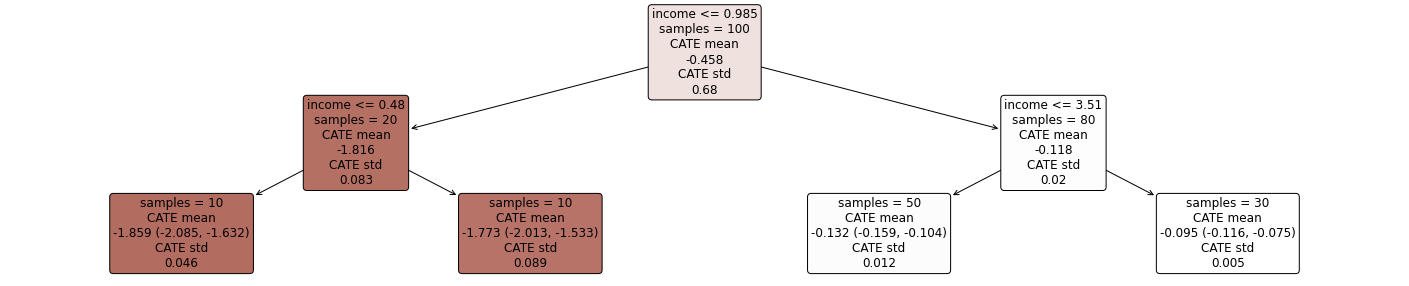
了解 EconML 的处理效果

EconML 包括可解释性工具，以更好地了解治疗效果。处理效果可能很复杂，但通常我们感兴趣的是简单的规则，这些规则可以区分积极响应的用户、保持中立的用户和对提议的更改做出消极响应的用户。

EconML 的 SingleTreeCateInterpreter 通过对任何 EconML 估计器输出的治疗效果训练单个决策树来提供可遍历性。在下图中，我们可以看到深红色用户对折扣的反应强烈，而白色用户对折扣的反应较轻。

intrp = SingleTreeCateInterpreter(include_model_uncertainty=True, max_depth=2, min_samples_leaf=10)
intrp.interpret(est_nonparam_dw, X_test)
plt.figure(figsize=(25, 5))
intrp.plot(feature_names=["income"], fontsize=12)

使用 EconML 做出策略决策

我们希望做出政策决策，以实现收入而不是需求最大化。在此方案中，

$\begin{align} Rev & = Y \cdot T \\ & = \exp^{log(Y)} \cdot T\\ & = \exp^{(\theta(X) \cdot log(T) + f(X,W) + \epsilon)} \cdot T \\ & = \exp^{(f(X,W) + \epsilon)} \cdot T^{(\theta(X)+1)} \end{align}$

随着价格的下降，只有当 $\theta(X)+1<0$ 时，收入才会增加。因此，这里设置 sample_treatment_cast=-1 来学习应该为哪些客户提供小额折扣以最大化收入。

EconML 库包含诸如 SingleTreePolicyInterpreter 的策略可解释性工具，该工具结合了处理成本和处理效应，用于学习关于哪些客户可以获利目标的简单规则。在下图中可以看到，模型建议对收入低于 $0.985$ 的人给予折扣，而对其他人则维持原价。

intrp = SingleTreePolicyInterpreter(risk_level=0.05, max_depth=2, min_samples_leaf=1, min_impurity_decrease=0.001)
intrp.interpret(est_nonparam_dw, X_test, sample_treatment_costs=-1)
plt.figure(figsize=(25, 5))
intrp.plot(feature_names=["income"], treatment_names=["Discount", "No-Discount"], fontsize=12)

现在，让我们将我们的策略与其他基线策略进行比较！我们的模型会向哪些客户提供小额折扣，对于此实验，我们将为这些用户设置 10% 的折扣水平。由于模型指定有误，因此我们不会期望具有较大折扣的良好结果。在这里，由于我们知道基本事实，因此我们可以评估此策略的价值。

# 定义函数来计算收入
def revenue_fn(data, discount_level1, discount_level2, baseline_T, policy):policy_price = baseline_T * (1 - discount_level1) * policy + baseline_T * (1 - discount_level2) * (1 - policy)demand = demand_fn(data, policy_price)rev = demand * policy_pricereturn rev

policy_dic = {}
# 我们的政策
policy = intrp.treat(X)
policy_dic["Our Policy"] = np.mean(revenue_fn(train_data, 0, 0.1, 1, policy))
## 之前的策略
policy_dic["Previous Strategy"] = np.mean(train_data["price"] * train_data["demand"])
##给大家折扣
policy_dic["Give Everyone Discount"] = np.mean(revenue_fn(train_data, 0.1, 0, 1, np.ones(len(X))))
## 不给折扣
policy_dic["Give No One Discount"] = np.mean(revenue_fn(train_data, 0, 0.1, 1, np.ones(len(X))))
## 遵循我们的政策，但团体给予-10%折扣，不建议给予折扣
policy_dic["Our Policy + Give Negative Discount for No-Discount Group"] = np.mean(revenue_fn(train_data,-0.1, 0.1, 1, policy))
## 给每个人-10% 的折扣
policy_dic["Give Everyone Negative Discount"] = np.mean(revenue_fn(train_data, -0.1, 0, 1, np.ones(len(X))))

# 获取策略汇总表
res = pd.DataFrame.from_dict(policy_dic, orient="index", columns=["Revenue"])
res["Rank"] = res["Revenue"].rank(ascending=False)
res

我们击败了基准政策！我们的政策获得的收入最高，除了提高 No-Discount 组的价格的政策。这意味着我们目前的基准价格很低，但我们细分用户的方式确实有助于增加收入！

结论

在项目中，我们演示了使用 EconML 和 DoWhy 的强大功能：

即使模型指定错误，也能正确估计处理效果
测试因果假设并调查结果估计的稳健性
解释由此产生的个体水平治疗效果
使策略决策击败先前和基线策略