【优选算法】前缀和

目录
- 一、[【模板】前缀和](https://www.nowcoder.com/practice/acead2f4c28c401889915da98ecdc6bf?tpId=230&tqId=2021480&ru=/exam/oj&qru=/ta/dynamic-programming/question-ranking&sourceUrl=%2Fexam%2Foj%3Fpage%3D1%26tab%3D%25E7%25AE%2597%25E6%25B3%2595%25E7%25AF%2587%26topicId%3D196)
- 二、[【模板】二维前缀和](https://www.nowcoder.com/practice/99eb8040d116414ea3296467ce81cbbc?tpId=230&tqId=2023819&ru=/exam/oj&qru=/ta/dynamic-programming/question-ranking&sourceUrl=%2Fexam%2Foj%3Fpage%3D1%26tab%3D%25E7%25AE%2597%25E6%25B3%2595%25E7%25AF%2587%26topicId%3D196)
- 三、[寻找数组的中心下标](https://leetcode.cn/problems/find-pivot-index/description/)
- 四、[除自身以外数组的乘积](https://leetcode.cn/problems/product-of-array-except-self/description/)
- 五、[和为 K 的子数组](https://leetcode.cn/problems/subarray-sum-equals-k/description/)
- 六、[和可被 K 整除的子数组](https://leetcode.cn/problems/subarray-sums-divisible-by-k/description/)
- 七、[连续数组](https://leetcode.cn/problems/contiguous-array/description/)
- 八、[矩阵区域和](https://leetcode.cn/problems/matrix-block-sum/description/)
- 结尾
一、【模板】前缀和
题目描述:

思路讲解:
简单的看过此题后,发现本题有一个暴力解法就是每给出两个下标,就遍历这个数组将这两个数字内的数字相加起来,若每次查询都是将数组从头到尾的相加起来,那么这个解法的时间复杂度就是O(q*n)。
本题还可以使用前缀和的思想来解决,前缀和能够快速求出数组中某一段连续区间的和。
我们仔细看一下题目可以发现题目给出的数组下标是从1开始的,我们这里定义一个同等规模的前缀和数组sum,并将sum[0]置为0,sum[i]记录的是下标为i时,题目给出数组下标1 ~ i所有数的和,通过下图我们可以发现sum[i]=sum[i-1]+arr[i],想要计算题目给出数组下标l ~ r之间所有数的和,就可以使题目给出数组中下标1 ~ r中所有数之减去下标1 ~ l-1中所有数,也就是sum中r下标的数减去下标为l-1下的数来即是答案也就是sum[r]-sum[l-1]。使用前缀和思想复杂度为,时间复杂度O(q) + 空间复杂度O(n)。至于这里数组为什么要以1开头是因为方便处理边界情况,若开头为0,并且l也为0就会导致越界的情况。

编写代码:
#include <iostream>
#include <vector>
using namespace std;int main()
{int n = 0 , q = 0;cin >> n >> q;vector<int> v;vector<long long> sum;sum.push_back(0);sum.reserve(n + 1);for(int i = 1 ; i < n + 1 ;i++){int num = 0;cin >> num;sum[i] = sum[i-1] + num;}int l = 0 , r = 0;while(q--){cin >> l >> r;cout << sum[r] - sum[l-1] << endl;}return 0;
}
// 64 位输出请用 printf("%lld")
二、【模板】二维前缀和
题目描述:

思路讲解:
本题可以使用暴力解法,将题目给出范围中所有的数遍历相加即可,那么本题的时间复杂度会达到O(q* n *m),并不是一个很好的方法。
本题可以使用前缀和的思想,定义一个二维前缀和数组dp,并且dp数组第0行和第0列的所有数都置为0,计算出前缀和的结果从第1行和第1列开始向dp中填充,dp[i][j]代表的是题目给出的数组(原数组)中[1,1]到[i,j]范围内所有数之和,通过下图我们发现如果我们想直接求得dp[x][y]也就是A+B+C+D并不好求,但是我们进行简单的转换A+B+C+D=(A+C)+(A+B)+D-A就很好求了,所以求dp[x][y]的公式就是dp[x][y]=dp[x][y-1]+dp[x-1][y]+vv[x][y]-dp[x-1][y-1]。

通过下图我们看出,如果想计算出原数组中[x1,y1]到[x2,y2]范围内所有数之和,使用整块面积(S)-A-B-C可以求得D,但是B和C却不得而知,所以我们可以转换思路,我们知道A,知道A+C,知道A+B,所以可以使用S-(A+C)-(A+B)+A来求得D,所以计算出原数组中[x1,y1]到[x2,y2]范围内所有数之和就可以使用dp[x2][y2] - dp[x2][y1-1] - dp[x1-1][y2] + dp[x1-1][y1-1]得到答案。上面提到的dp数组第0行和第0列的所有数都置为0,是为了防止上面计算时出现越界的情况。

编写代码:
#include <iostream>
#include <vector>
using namespace std;int main() {int n = 0 , m = 0 , q = 0;vector<vector<int>> vv;vector<vector<long long>> dp;cin >> n >> m >> q;vv.resize(n + 1);dp.resize(n + 1);// 初始化dp二维数组for(int i = 0 ; i < n + 1 ; i++){vv[i].resize(m + 1);dp[i].resize(m + 1);}for(int i = 0 ; i < n + 1 ;i++){vv[i][0] = 0;dp[i][0] = 0;}for(int i = 0 ; i < m + 1 ;i++){vv[0][i] = 0;dp[0][i] = 0;}// 初始化vv二维数组for(int i = 1 ; i < n + 1 ; i++)for(int j = 1 ; j < m + 1 ; j++)cin >> vv[i][j];// 计算补充dp二维数组for(int i = 1 ; i < n + 1 ; i++){for(int j = 1 ; j < m + 1 ; j++){dp[i][j] = dp[i][j-1] + dp[i-1][j] - dp[i-1][j-1] + vv[i][j];}}while(q--){int x1 , y1 , x2 , y2;cin >> x1 >> y1 >> x2 >> y2;cout << dp[x2][y2] - dp[x2][y1-1] - dp[x1-1][y2] + dp[x1-1][y1-1] << endl;}return 0;
}
// 64 位输出请用 printf("%lld")
三、寻找数组的中心下标
题目描述:

思路讲解:
本题可以使用暴力解法,遍历数组的每一个位置,并遍历分别计算当前位置左边和右边所有数的和,从头这样操作有左边数之和等于右边数之和,返回当前位置,若没有找到则返回-1,但是这样操作会使时间复杂度达到O(q*n2),显然不是一个很好的解法。
这里可以使用前缀和的思想定义两个数组,前缀和数组f,后缀和数组g,f[i]记录的是数组num中下标i-1之前所有数的和,f[i]=f[i-1]+nums[i-1],g[i]记录的是数组num中下标i+1以后所有数之和,g[i]=g[i+1]+nums[i+1],做完这些以后,只需要从头遍历数组下标,判断f[i]是否等于g[i],若相同返回当前下标,一直不相等则返回-1。这里需要注意一下边界问题,当i为0和n-1时,会分别导致数组f和数组g越界,所以我们需要提前对这两个位置做处理,f[0]=0,g[n-1]=0。还需要注意的是f数组需要从左往右开始计算,数组g需要从右向左计算。
编写代码:
class Solution {
public:int pivotIndex(vector<int>& nums) {vector<int> f; // 记录前缀和vector<int> d; // 记录后缀和int numsLen = nums.size();f.reserve(numsLen + 1);d.reserve(numsLen + 1);f[0] = 0 , d[numsLen] = 0 , d[numsLen-1] = 0;// 前缀和记录的是除当前数字外,前面所有数字的和for(int i = 1 ; i <= numsLen ; i++)f[i] = f[i-1] + nums[i-1];// 后缀和记录的是除当前位置外,后面所有数字的和for(int i = numsLen - 2 ; i >= 0 ; i--)d[i] = d[i+1] + nums[i+1];for(int i = 0 ; i < numsLen ;i++){if(f[i] == d[i])return i;}return -1;}
};
四、除自身以外数组的乘积
题目描述:

思路讲解:
本题可以使用暴力解法,遍历数组的每一个位置,并遍历并计算除下标i以外当所有数的积,但是这样操作会使时间复杂度达到O(q*n2),显然不是一个很好的解法。
本题与上一题的思路基本一致,这里可以使用前缀和的思想定义两个数组,前缀和数组f,后缀和数组g,f[i]记录的是数组num中下标i-1之前所有数的积,f[i]=f[i-1]+nums[i-1],g[i]记录的是数组num中下标i+1以后所有数之积,g[i]=g[i+1]+nums[i+1],做完这些以后,只需要从头遍历数组下标,每遍历一个下标就将f[i]*g[i]放到对应的ans数组中。这里需要注意一下边界问题,当i为0和n-1时,会分别导致数组f和数组g越界,所以我们需要提前对这两个位置做处理,f[0]=1,g[n-1]=1。还需要注意的是f数组需要从左往右开始计算,数组g需要从右向左计算。
编写代码:
class Solution {
public:vector<int> productExceptSelf(vector<int>& nums) {vector<int> f; // 记录前缀积vector<int> d; // 记录后缀积vector<int> ans;int numsLen = nums.size();f.reserve(numsLen + 1);d.reserve(numsLen + 1);f[0] = 1 , d[numsLen] = 1 , d[numsLen - 1] = 1;// 除当前位置数字,所有前面所有数字之积for(int i = 1 ; i <= numsLen ; i++)f[i] = f[i-1] * nums[i-1];// 除当前位置数字,所有后面所有数字之积for(int i = numsLen - 2; i >= 0 ;i--)d[i] = d[i+1] * nums[i+1];for(int i = 0 ; i < numsLen ; i++)ans.push_back(f[i] * d[i]);return ans;}
};
五、和为 K 的子数组
题目描述:

思路讲解:
本题可以使用暴力解法,遍历出数组num所以的子数组,并得到每个子数组的和,记录和等于k的子数组的个数。这样做会使本题的时间复杂度达到O(n2),并不是一个很好的方法。
本题可以使用前缀和与哈希表的思想来解决本题,当一个前缀和减去另一个前缀和等于k,就代表着有一段连续的子区间相加等于k,这里定义一个变量sum来代替前缀和数组,sum代表的是num数组中第i位之前(包括第i位)所有数之和,定义一个哈希表unordered_map<int,int> um,um中存储的是第i位之前(不包括第i位)的前缀和的数值和对应出现的次数。
这里有三个点需要注意:
- 前缀和加入哈希表的时机
在计算i位置时,哈希表中只存储[0,i-1]位置的前缀和 - 并不需要真的创建一个前缀和数组
由于我们哈希表中需要存储的是前缀和和前缀和出现的次数,我们只需要定义一个变量sum,让它来记录当前位置的前缀和,然后再添加到哈希表中即可。 - 假如整个前缀和数组之和等于k
我们只需要在最开始的时候在哈希表中添加一个前缀和为0出现过一次即可解决这个问题。由于我最开始sum的值就为0,当um[sum]++;时就处理了这个问题。

编写代码:
class Solution {
public:// 以i结尾的前缀和 --> 在i之前sum[i]-kint subarraySum(vector<int>& nums, int k) {unordered_map<int,int> um;int numsLen = nums.size() - 1;int count = 0;int sum = 0; // 前缀和for(int i = 0 ; i <= numsLen ;i++){// 这里加入的前缀和是前一个位置的前缀和um[sum]++;sum += nums[i];if(um.count(sum-k))count += um[sum - k];}return count;}
};
六、和可被 K 整除的子数组
题目描述:

思路讲解:
本题可以使用暴力解法,遍历出数组num所以的子数组,并得到每个子数组的积,记录能整除k的子数组的个数。这样做会使本题的时间复杂度达到O(n2),并不是一个很好的方法。
本题与上一题的思路有些相似,可以使用前缀和(实际上是前缀积)的思想,在以前学习数学的时候学习过同余定理,我们知道(a - b)/p = k······0 可以推出 a % p == b % p,那么只要两个数(a,b)同时除以另一个数(p)得到的余数相同,那么两数的差一定会被另一个数(p)整除,所以在题目中当两个前缀和除以k得到的余数相同,两个前缀和的差就一定能被k正常,就代表着有一段连续的子区间相加能被k整除,这里定义一个变量sum来代替前缀和数组,sum代表的是num数组中第i位之前(包括第i位)所有数之和,定义一个哈希表unordered_map<int,int> um,um中存储的是第i位之前(不包括第i位)的前缀和对k进行取模得到的数值和对应出现的次数。
这里还有个小细节就是在C /C++中,负数对正数取模得到的数与0相比一定是相等或小于,会导致我们这里的判断出现问题,所以这里要对负数对正数取模得到的数进行修正,我们可以使用(a % p + p)%p对结果进行修正,每个存入哈希表的前缀和都要对k进行取模再进行修正后才能放入哈希表中。
编写代码:
class Solution {
public:int subarraysDivByK(vector<int>& nums, int k) {// (a - b)/p = k······0 --> a % p == b % p// C++中,负数%正数为负数,负数%正数修正 (a % p + p)%punordered_map<int,int> um;int count = 0;int sum = 0;for(int i = 0 ; i < nums.size() ; i++){// 前缀和入哈希表um[(sum % k + k) % k]++;sum += nums[i];// sum % k = x % k (x 代表前缀和)if(um.count((sum % k + k) % k))count += um[(sum % k + k) % k];}return count;}
};
七、连续数组
题目描述:

思路讲解:
这里使用暴力解法的方式就不做讲解了,也不推荐大家使用暴力解法。
如果这里大家按照题目的思路来做,可能会有点不好解决,但是如果将0该为-1,大家思考一下会不会一下就有思路了。
这里使用前缀和的思想,当下标为i和j位置的前缀和相等那么就代表着原数组在[i,j]这个区间中1和-1的数量是相同的,也就是0和1的数量是相同的。定义一个变量sum,sum代表的是num数组中第i位之前(包括第i位)所有数之和,定义一个哈希表unordered_map<int,int> um,um中存储的是第i位之前(不包括第i位)的前缀和的数值和对应出现的位置的下标。注意题目需要找到含有相同数量的 0 和 1 的最长连续子数组,所以当一个前缀和在哈希表中存在,那么就不需要将其加入哈希表,也不需要修改对应哈希表中的下标。
这里还有两个小细节需要处理一下:
- 当从下标 i 位置上的前缀和为0
当数组中没有元素时,前缀和为0,为了处理这种特殊情况,我们需要在哈希表提前加入一组数据{0,-1}。 - 最长长度的计算方式
使用当前下标减去哈希表中相同前缀和的下标也就是i - um[sum]。
编写代码:
class Solution {
public:int findMaxLength(vector<int>& nums) {unordered_map<int, int> um; // 记录前缀和 和 下标int numsLen = nums.size();;int MaxLen = 0; // 记录答案int sum = 0; // 前缀和um.insert(make_pair(sum, -1)); // 没元素时,前缀和为0for (int i = 0; i < numsLen; i++){// 将0变为-1if (nums[i] == 0)sum -= 1;elsesum += 1;// 这里需要判断sum是否在um中存在// 否则后面会将sum直接入um,并且second为0if (um.count(sum) != 0 && MaxLen < i - um[sum])MaxLen = i - um[sum];// 由于这里需要最长子数组// 所以这里前缀和相同的下标越小越好// 所以出现过的前缀和后面都不需要入umif (um.count(sum) == 0)um.insert(make_pair(sum, i));}return MaxLen;}
};
八、矩阵区域和
题目描述:

思路讲解:
这里使用暴力解法的方式就不做讲解了,也不推荐大家使用暴力解法。
很多人可能但看题目看不出来这题要干什么,以下图为例,i和j是对应需要在ans矩阵中填入答案的下标,k是在下标处向上下左右延展k个位置,将延展后在原数组mat中形成的矩形中所有的数字相加得到的数,填入到数组ans中,需要注意的是越界的位置全部不需要,只需要将有效下标上的数字相加。

本题可以使用前缀和的思想,定义一个二维前缀和数组dp,并且dp数组第0行和第0列的所有数都置为0,计算出前缀和的结果从第1行和第1列开始向dp中填充,dp[i][j]代表的是题目给出的数组(原数组)中[1,1]到[i,j]范围内所有数之和,通过下图我们发现如果我们想直接求得dp[x][y]也就是A+B+C+D并不好求,但是我们进行简单的转换A+B+C+D=(A+C)+(A+B)+D-A就很好求了,需要注意的是dp数组是从第1行第1列开始存储数据的,而原数组mat是从第0行和第0列开始存储数据的,为了让两者的位置对应,所以求dp[x][y]的公式就是dp[x][y]=dp[x][y-1]+dp[x-1][y]+mat[x-1][y-1]-dp[x-1][y-1]。

在本篇文章中的二位前缀和这道题的基础上,我们知道如何使用二位前缀和,只要我们知道所需要的区域的左上角的下标[x1,y1]和右下角的下标[x2,y2]就能解决本道题,x1在i的基础上向上移动k位,y1在j的基础上向左移动k位,x2在i的基础上向下移动k位,y2在j的基础上向右移动k位,但是这两个下标是存在越界的风险的,所以在获取这两个下标时就要做处理,例如坐标小于1就按1处理,大于n就按n处理,这里的1和n是对应着二位前缀和数组的,具体可以看下面代码是如何操作的。想要计算出原数组中[x1,y1]到[x2,y2]范围内所有数之和,看下图我们可以使用整块面积(S)-A-B-C可以求得D,但是B和C却不得而知,所以我们可以转换思路,我们知道A,知道A+C,知道A+B,所以可以使用S-(A+C)-(A+B)+A来求得D,加上我们需要返回的二维数组ans从第0行和第0列开始存储数据的,为了让dp数组与ans数组对应,那么数组ans中元素的计算方式就是,ans[i-1][j-1]=dp[x2][y2] - dp[x2][y1-1] - dp[x1-1][y2] + dp[x1-1][y1-1]得到答案,这里的i和j也是对应着二位前缀和数组最开始。上面提到的dp数组第0行和第0列的所有数都置为0,是为了防止上面计算时出现越界的情况。

编写代码:
class Solution {
public:vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {int n = mat.size() , m = mat[0].size();vector<vector<int>> dp(n + 1 , vector<int>(m + 1));vector<vector<int>> ans(n , vector<int>(m));// 前缀块和for(int i = 1 ; i < n + 1 ;i++){for(int j = 1 ; j < m + 1 ; j++){dp[i][j] = dp[i][j-1] + dp[i-1][j] - dp[i-1][j-1] + mat[i-1][j-1];}}for(int i = 1 ; i < n + 1 ;i++){for(int j = 1 ; j < m + 1 ; j++){// 防止越界int x1 = max(i-k,1), y1 = max(j-k,1);int x2 = min(i+k,n), y2 = min(j+k,m);// ans的下标与dp下标需要对应ans[i-1][j-1] = dp[x2][y2] - dp[x2][y1-1] - dp[x1-1][y2] + dp[x1-1][y1-1];}}return ans;}
};
结尾
如果有什么建议和疑问,或是有什么错误,大家可以在评论区中提出。
希望大家以后也能和我一起进步!!🌹🌹
如果这篇文章对你有用的话,希望大家给一个三连支持一下!!🌹🌹
相关文章:
【优选算法】前缀和
目录 一、[【模板】前缀和](https://www.nowcoder.com/practice/acead2f4c28c401889915da98ecdc6bf?tpId230&tqId2021480&ru/exam/oj&qru/ta/dynamic-programming/question-ranking&sourceUrl%2Fexam%2Foj%3Fpage%3D1%26tab%3D%25E7%25AE%2597%25E6%25B3%2595…...

Spring Bean 的生命周期详解
所谓万物皆对象,对于一个 bean 而言,从出生到死亡,他要经历哪些阶段呢? 生命周期 理解对象的生命周期,可以帮助我们更好的做一些扩展。 一个对象从被创建到被垃圾回收,可以大致分为这 5 个阶段:…...

MySQL【知识改变命运】12
视图 1:什么是视图2:创建视图使用视图(视图的好处)2.1.隐藏敏感字段2.2.对外提供统一访问3:视图和真实表进⾏表连接查询 4:修改视图数据4.1:通过真实表修改数据,会影响视图4.2&#…...
)
shell编程(完整版)
目录 一、shell脚本解释器 二、shell脚本的执行 三、变量的使用 四、永久环境变量 按用户设置永久环境变量 文件路径: 示例步骤: 删除永久环境变量 五、脚本程序传递参数怎么实现 六、用编程进行数学运算 shell中利用expr进行运算 运算与变量…...

数字逻辑(一)——导论
1.导论 1.1什么是数字逻辑? 数字逻辑是指在数字电路设计、计算机科学领域中对于离散的二进制信号进行逻辑处理、运算、存储和传输的基本原理和方法。 1.2数字量和模拟量的区别 数字量:在时间上和数量上都是离散的、不连续的物理量。模拟量࿱…...

量化交易系统开发-实时行情自动化交易-4.4.做市策略
19年创业做过一年的量化交易但没有成功,作为交易系统的开发人员积累了一些经验,最近想重新研究交易系统,一边整理一边写出来一些思考供大家参考,也希望跟做量化的朋友有更多的交流和合作。 接下来继续说说做市策略原理。 做市策…...

《线性代数的本质》
之前收藏的一门课,刚好期末复习,顺便看一看哈哈 课程链接:【线性代数的本质】合集-转载于3Blue1Brown官方双语】 向量究竟是什么 线性代数中最基础、最根源的组成部分就是向量,需要先明白什么是向量 不同专业对向量的看法 物理专…...

Gbase8s 允许内置用户创建用户以及创建只读权限用户以及利用角色管理普通用户权限
Gbase8s 允许内置用户创建用户以及创建只读权限用户以及利用角色管理普通用户权限 普通安装实例创建数据库以后,DBA权限只有gbasedbt用户。gbasdbt可以创建普通用户,并且给普通用户赋予库及权限或者表级权限。 但是gbasedbt用户口令和操作系统相关,所以想在不提供gbasedbt的…...

24/11/25 视觉笔记 深度传感器和手势识别
本章的目的是开发一个应用程序,使用深度传感器的输出实时检测和跟踪简单的手势。该应用程序将分析每个已捕捉的帧。并执行以下任务。 手部区域分割:通过分析Kinect传感器的深度图输出,在每一帧中提取用户的手部区域,这是通过阈值…...

迄今为止的排序算法总结
迄今为止的排序算法总结 7.10 迄今为止的排序算法总结复杂度和稳定性时间复杂度测试程序sortAlgorithm.hsortAlgorithm.cpptest.cpp 时间复杂度测试结果 7.10 迄今为止的排序算法总结 复杂度和稳定性 排序算法平均情况最好情况最坏情况稳定性空间复杂度选择排序O(n^2)O(n^2)O…...

HTML和CSS 表单、表格练习
HTML和CSS 表格练习 <!DOCTYPE html> <html lang"zh-CN"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>HTML表格练习</title>…...

H5流媒体播放器EasyPlayer.js网页直播/点播播放器如果H.265视频在播放器上播放不流畅,可以考虑的解决方案
随着流媒体技术的迅速发展,H5流媒体播放器已成为现代网络视频播放的重要工具。其中,EasyPlayer.js网页直播/点播播放器作为一款功能强大的H5播放器,凭借其全面的协议支持、多种解码方式以及跨平台兼容性,赢得了广泛的关注和应用。…...

Http 转 https 中 Nginx 的详细配置过程
摘要 本节将简要介绍从 HTTP 到 HTTPS 的配置过程,并完整展示 Nginx 的相关配置信息。 经过两天断断续续的调试,终于将 http 变成 https 了。现在说说这个安装 ssl 证书的过程。 服务器是在某云上。这个过程大致分为三个步骤:申请 ssl 证书、…...
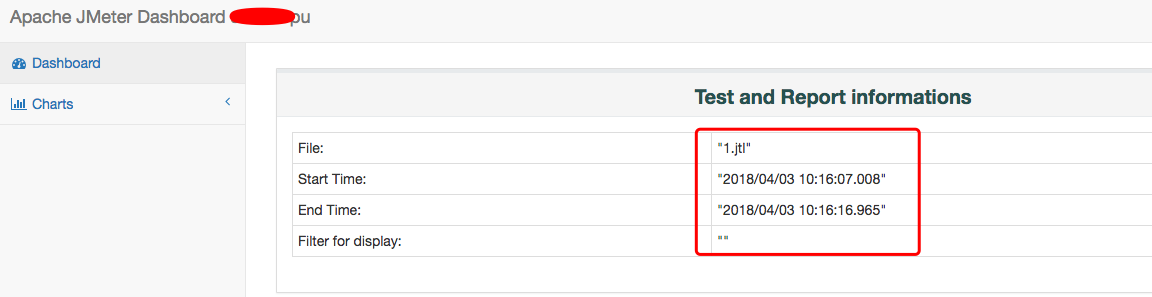
【测试工具JMeter篇】JMeter性能测试入门级教程(二)出炉,测试君请各位收藏了!!!
上篇文章:CSDN 我们介绍了JMeter的一些原理介绍,以及安装配置和启动流程,本文我们就来讲讲JMeter如何使用。 一、JMeter目录结构组成 1. 根目录 Jmeter安装包解压后的根目录如下图: 1.1 backups目录:脚本备份目录&am…...

Otter 安装流程
优质博文:IT-BLOG-CN 一、背景 随着公司的发展,订单库的数据目前已达到千万级别,需要进行分表分库,就需要对数据进行迁移,我们使用了otter,这里简单整理下,otter 的安装过程,希望对…...

一文学会Golang里拼接字符串的6种方式(性能对比)
g o l a n g golang golang的 s t r i n g string string类型是不可修改的,对于拼接字符串来说,本质上还是创建一个新的对象将数据放进去。主要有以下几种拼接方式 拼接方式介绍 1.使用 s t r i n g string string自带的运算符 ans ans s2. 使用…...

【笔记】Linux下编译Python3.10.15为动态库同时正确处理OpenSSL3依赖
之前自己第一次编译Python后发现pip会提示无法使用SSL,后来了解到是自己编译时没有配置OpenSSL。这个过程有点曲折,里面有一个坑,怕忘记于是写博客记录一下。 首先是下载OpenSSL,Python3.10.15支持此时最新版的OpenSSL 3.4.0&…...

Go语言获取客户端真实IP
在一些需求中,服务器需要记录客户端的ip地址,要获取ip地址,则需要有http.Request的对象参数传入,以下代码直接放在util中使用。 文件名:ip_utils.go package utilsimport ("context""github.com/spf1…...
)
大模型论文速递(11.23-11.25)
BlueLM-V3B 关键词:动态分辨率,图像放大,适应性网格化方法 研究问题:如何改进现有的动态分辨率匹配方法以减少在模型训练和部署中的计算复杂度? 方法: 分析现有动态分辨率匹配算法(如LLaVA-…...
)
维护在线重做日志(二)
迁移和重命名 可以使用操作系统命令重新定位重做日志,然后使用ALTER DATABASE语句使数据库知道它们的新名称(位置)。这个过程是必要的,例如,如果当前用于一些重做日志文件的磁盘将被删除,或者如果数据文件…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...
