计算机的错误计算(一百六十六)
摘要 探讨 MATLAB 关于算式
的计算误差。
例1. 已知
计算
直接贴图吧:
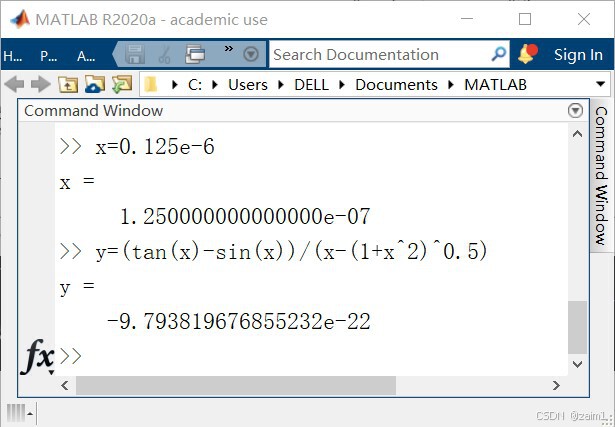
然而,16位的正确结果为 -0.9765626220703239e-21(ISRealsoft 提供)。这样,MATLAB输出的有效数字的错误率为 (16-2)/16 = 87.5% .
注:可参看计算机的错误计算(一百二十三)。
参考文献
[1] Ward Cheney, David Kincaid. Numerical Mathematics and Computing. 6th Ed. CA: Thomson Higher Education, 2008, p, 69
相关文章:

计算机的错误计算(一百六十六)
摘要 探讨 MATLAB 关于算式 的计算误差。 例1. 已知 计算 直接贴图吧: 然而,16位的正确结果为 -0.9765626220703239e-21(ISRealsoft 提供)。这样,MATLAB输出的有效数字的错误率为 (16-2)/16 87.5% . 注&…...

typeof 和 as 关键字
在编程语言中,类型系统是确保代码正确性和可维护性的关键。JavaScript和TypeScript作为现代前端开发的两大支柱,它们在处理类型方面有着不同的机制。本文将探讨typeof和as这两个关键字在JavaScript和TypeScript中的应用,帮助开发者更好地理解…...

Python酷库之旅-第三方库Pandas(237)
目录 一、用法精讲 1116、pandas.tseries.offsets.BusinessHour.is_year_end方法 1116-1、语法 1116-2、参数 1116-3、功能 1116-4、返回值 1116-5、说明 1116-6、用法 1116-6-1、数据准备 1116-6-2、代码示例 1116-6-3、结果输出 1117、pandas.tseries.offsets.Cu…...

git提交到远程仓库如何撤回?
git提交到远程仓库如何撤回? 要撤回已经提交到远程仓库的更改,你可以使用以下步骤: 首先,确保你的本地仓库是最新状态。如果不是,请先执行 git pull 来更新你的本地仓库。 使用 git log 查看提交历史,找到你想要撤回…...

微信小程序常用全局配置项及窗口组成部分详解
微信小程序常用全局配置项及窗口组成部分详解 引言 微信小程序作为一种新兴的应用形态,凭借其轻量级、便捷性和丰富的功能,已成为开发者和用户的热门选择。在开发小程序的过程中,了解全局配置项和窗口组成部分是至关重要的。本文将详细介绍微信小程序的常用全局配置项及窗…...

ThingsBoard规则链节点:Azure IoT Hub 节点详解
目录 引言 1. Azure IoT Hub 节点简介 2. 节点配置 2.1 基本配置示例 3. 使用场景 3.1 数据传输 3.2 数据分析 3.3 设备管理 4. 实际项目中的应用 4.1 项目背景 4.2 项目需求 4.3 实现步骤 5. 总结 引言 ThingsBoard 是一个开源的物联网平台,提供了设备…...

「Mac玩转仓颉内测版32」基础篇12 - Cangjie中的变量操作与类型管理
本篇将深入探讨 Cangjie 编程语言中的变量操作与类型管理,涵盖变量的定义、作用域、类型推断、常量、变量遮蔽、类型转换等方面的知识。通过这些概念的学习,开发者将更好地理解和灵活掌握变量的使用与管理技巧。 关键词 变量定义类型推断常量变量作用域…...

【Android】RecyclerView回收复用机制
概述 RecyclerView 是 Android 中用于高效显示大量数据的视图组件,它是 ListView 的升级版本,支持更灵活的布局和功能。 我们创建一个RecyclerView的Adapter: public class MyRecyclerView extends RecyclerView.Adapter<MyRecyclerVie…...

麒麟系统性能瓶颈分析
1.使用率,表示资源用于服务的时间或容量百分比。100% 的使用率,表示容量已经用尽或者全部时 间都用于服务。 2. 饱和度,表示资源的繁忙程度,通常与等待队列的长度相关。100% 的饱和度,表示资源无法接受 更多的请求。 3…...

Java二分查找+冒泡排序
二分查找在编程中是用来查找目标元素在有序数组中的位置,并返回目标元素的索引 先给定一个有序数组,在创建一个方法来进行二分 主要思想是:根据数组具有下标的特点来分别计算,最左边的索引,以及最右边的索引,在判断目标元素与中间元素的大小,如果目标元素小于中间元素,我们可…...

(三)手势识别——动作识别应用【代码+数据集+python环境(免安装)+GUI系统】
(三)手势识别——动作识别应用【代码数据集python环境(免安装)GUI系统】 (三)手势识别——动作识别【代码数据集python环境GUI系统】 背景意义 随着互联网的普及和机器学习技术的进一步发展,手…...

大数据实战——MapReduce案例实践
🌟欢迎来到 我的博客 —— 探索技术的无限可能! 🌟博客的简介(文章目录) 大数据实战——MapReduce案例实践 一.过程分析(截图)1. 确定Hadoop处于启动状态2. 在/usr/local/filecotent…...
)
OpenCV基础(3)
1.图像直方图 1.1.像素统计 计算图像均值: Scalar cv::mean(InputArray src,InputArray masknoArray()); src:输入图像mask:掩膜层过滤 返回值是对输入图像通道数计算均值后的Scalar对象 计算图像均值与方差: void cv::meanSt…...

大语言模型---RewardBench 介绍;RewardBench 的主要功能;适用场景
文章目录 1. RewardBench 介绍2. RewardBench 的主要功能3. 适用场景 1. RewardBench 介绍 RewardBench: Evaluating Reward Models是一个专门用于评估 Reward Models(奖励模型) 的公开平台,旨在衡量模型在多种任务上的性能,包括…...

泷羽sec-linux
基础之linux 声明! 学习视频来自B站up主 泷羽sec 有兴趣的师傅可以关注一下,如涉及侵权马上删除文章,笔记只是方便各位师傅的学习和探讨,文章所提到的网站以及内容,只做学习交流,其他均与本人以及泷羽sec团…...

栈、队列、链表
一、栈 1. 定义 栈是一种线性数据结构,遵循后进先出(LIFO, Last In First Out)的原则。这意味着最后被添加到栈中的元素将会是最先被移除的元素。 2. 基本操作 Push:将一个元素添加到栈顶。Pop:移除并返回栈顶的元…...

【maven】配置下载私有仓库的快照版本
1、setting.xml配置 <settings xmlns"http://maven.apache.org/SETTINGS/1.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org/SETTINGS/1.0.0https://maven.apache.org/xsd/settings-1.0.0.…...
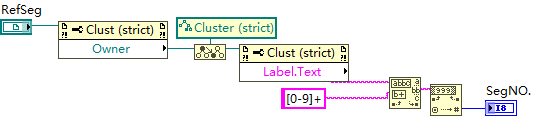
LabVIEW引用类型转换问题
一、问题描述 在LabVIEW中,refnum(引用编号)用于引用各种资源,如文件、队列、控件等。这些引用是与具体类型相关的,通常情况下,LabVIEW会根据引用的类型自动进行处理。然而,当不同类型的引用需…...

GUI智能代理:用AI代理玩米哈游游戏《崩坏》
项目名称:The Dawn of GUI Agent研究对象:Claude 3.5 Computer Use特点:首个公测版GUI智能代理系统 技术创新 首创性:这是首个提供公测版图形界面控制功能的前沿AI模型。交互方式:实现了从自然语言到桌面操作的端到端控制,用户可以通过简单的自然语言指令完成复杂的桌面…...

系统思考—环路图的好处
每次内部学习,我们都会用系统环路图拆解那些动态性复杂的议题。这不仅仅是我们教学的工具,更是我们在实践中不断应用和打磨的利器。 我常在课程中和大家分享,什么原因要持续使用系统环路图? 🎯 1. 落地全局思维 环路图…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...
