单点修改,区间求和或区间询问最值(线段树)
【题目描述】
给定一个长度为n的非负整数序列,接下来有m次操作,操作共有3种:一是修改序列中某个元素的大小,二是求某个区间的所有元素的和,三是询问某个区间的最大值。整数序列下标从1开始。n<=10^5, m<=10^5。
【输入描述】
第一行2个整数n和m, 分别 表示整数序列的元素个数和操作次数;
接下来一行就是这n个非负整数, 每个整数都不超过10^8;
接下来m行,每行都有三个整数k, a, b;
如果k是0的话,就表示把原序列中的第a个位置上的数改为b,b也是不超过10^8的非负整数。
如果k是1的话,就表示询问区间[a, b]的最大值, 如果k是2的话就表示询问区间[a, b]的元素和。
【输出描述】
对于每个k为1或2的询问输出相对应的结果,每个输出结果占一行。
【输入样例】
10 4 5 2 3 4 7 9 5 8 6 2 0 5 9 1 2 5 0 8 6 2 7 10
【输出样例】
9 19
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 100010;
struct node {int l, r, mx;ll s;
};
node xdt[4*N];
int n, m, p, l, r, x, y, a[N];
void build(int k, int l, int r) {xdt[k].l = l; xdt[k].r = r;if (l==r) {xdt[k].s = a[l];xdt[k].mx = a[l];return;}int mid = (xdt[k].l + xdt[k].r) / 2;build(k*2, l, mid);build(k*2+1, mid+1, r);xdt[k].s = xdt[k*2].s + xdt[k*2+1].s;xdt[k].mx = max(xdt[k*2].mx, xdt[k*2+1].mx);
}
void change(int k, int x, int y) {if (xdt[k].l == x && xdt[k].r == x) {xdt[k].s = y;xdt[k].mx = y;return; }int mid = (xdt[k].l + xdt[k].r) / 2;if (x <= mid) change(k*2, x, y);else change(k*2+1, x, y);xdt[k].s = xdt[k*2].s + xdt[k*2+1].s;xdt[k].mx = max(xdt[k*2].mx, xdt[k*2+1].mx);
}
long long find_s(int k, int l, int r) {if (xdt[k].l == l && xdt[k].r == r) {return xdt[k].s;}int mid = (xdt[k].l + xdt[k].r) / 2;if (l > mid) return find_s(k*2+1, l, r);if (r <= mid) return find_s(k*2, l, r);return find_s(k*2, l, mid) + find_s(k*2+1, mid+1, r);
}
int find_mx(int k, int l, int r) {if (xdt[k].l == l && xdt[k].r == r) {return xdt[k].mx;}int mid = (xdt[k].l + xdt[k].r) / 2;if (l > mid) return find_mx(k*2+1, l, r);if (r <= mid) return find_mx(k*2, l, r);return max(find_mx(k*2, l, mid), find_mx(k*2+1, mid+1, r));
}
int main() {scanf("%d%d", &n, &m);for (int i=1; i<=n; i++) scanf("%d", &a[i]);build(1, 1, n);for (int i=1; i<=m; i++) {scanf("%d", &p);if (p==0) {scanf("%d%d", &x, &y);change(1, x, y);} if (p==1) {scanf("%d%d", &l, &r);printf("%d\n", find_mx(1, l, r));}if (p==2) {scanf("%d%d", &l, &r);printf("%lld\n", find_s(1, l, r));}}return 0;
}相关文章:
)
单点修改,区间求和或区间询问最值(线段树)
【题目描述】 给定一个长度为n的非负整数序列,接下来有m次操作,操作共有3种:一是修改序列中某个元素的大小,二是求某个区间的所有元素的和,三是询问某个区间的最大值。整数序列下标从1开始。n<10^5, m<10^5。 …...

线性代数空间理解
学习线性代数已经很久,但是在使用过程中仍然还是不明所以,比如不知道特征向量和特征值的含义、矩阵的相乘是什么意思、如何理解矩阵的秩……。随着遇到的次数越来越多,因此我决定需要对线性代数的本质做一次深刻的探讨了。 本次主要是参考了3…...
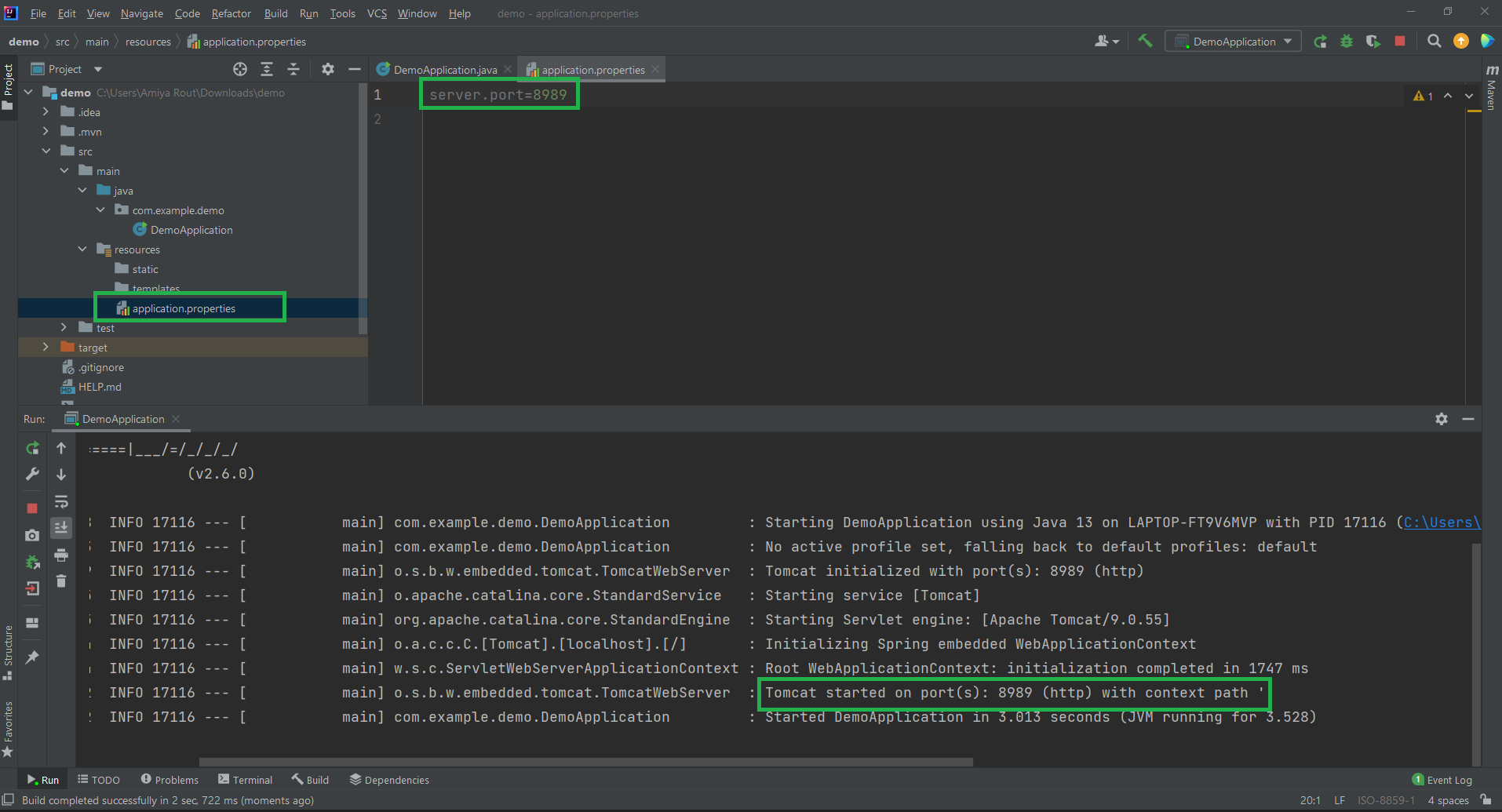
Spring Boot教程之五:在 IntelliJ IDEA 中运行第一个 Spring Boot 应用程序
在 IntelliJ IDEA 中运行第一个 Spring Boot 应用程序 IntelliJ IDEA 是一个用 Java 编写的集成开发环境 (IDE)。它用于开发计算机软件。此 IDE 由 Jetbrains 开发,提供 Apache 2 许可社区版和商业版。它是一种智能的上下文感知 IDE,可用于在各种应用程序…...

C51相关实验
C51相关实验 LED //功能:1.让开发板的LED全亮,2,点亮某一个LED,3.让LED3以5Hz的频率闪动#include "reg52.h"#define LED P2 sbit led1 LED^1;void main(void) {LED 0xff;//LED全灭led1 0;while(1)//保持应用程序不退出{} }LED 输出端是高…...

docker离线安装linux部分问题整理
0:离线安装docker过程命令 echo $PATH tar -zxvf docker-26.1.4.tgz chmod 755 -R docker cp docker/* /usr/bin/ root 权限 vim /etc/systemd/system/docker.service --------- [Unit] DescriptionDocker Application Container Engine Documentationhttps://docs.do…...

ISUP协议视频平台EasyCVR萤石设备视频接入平台银行营业网点安全防范系统解决方案
在金融行业,银行营业厅的安全保卫工作至关重要,它不仅关系到客户资金的安全,也关系到整个银行的信誉和运营效率。随着科技的发展,传统的安全防护措施已经无法满足现代银行对于高效、智能化安全管理的需求。 EasyCVR视频汇聚平台以…...

递推概念和例题
一、什么是递推 递推算法以初始值为基础,用相同的运算规律,逐次重复运算,直至求出问题的解,它的本质是按照固定的规律逐步推出(计算出)下一步的结果 这种从“起点”重复相同的的方法直至到达问题的解&…...

开发工具 - VSCode 快捷键
以下是一些常用的 VS Code 快捷键(Windows、macOS 和 Linux 均适用,略有不同): 常用快捷键 功能Windows/LinuxmacOS打开命令面板Ctrl Shift P 或 F1Cmd Shift P打开文件Ctrl OCmd O保存文件Ctrl SCmd S全部保存Ctrl K,…...

数据库的联合查询
数据库的联合查询 简介为什么要使⽤联合查询多表联合查询时MYSQL内部是如何进⾏计算的构造练习案例数据案例:⼀个完整的联合查询的过程 内连接语法⽰例 外连接语法 ⽰例⾃连接应⽤场景示例表连接练习 ⼦查询语法单⾏⼦查询多⾏⼦查询多列⼦查询在from⼦句中使⽤⼦查…...

【人工智能】基于PyTorch的深度强化学习入门:从DQN到PPO的实现与解析
《Python OpenCV从菜鸟到高手》带你进入图像处理与计算机视觉的大门! 深度强化学习(Deep Reinforcement Learning)是一种结合深度学习和强化学习的技术,适用于解决复杂的决策问题。深度Q网络(DQN)和近端策略优化(PPO)是其中两种经典的算法,被广泛应用于游戏、机器人控…...

【深度学习】【RKNN】【C++】模型转化、环境搭建以及模型部署的详细教程
【深度学习】【RKNN】【C】模型转化、环境搭建以及模型部署的详细教程 提示:博主取舍了很多大佬的博文并亲测有效,分享笔记邀大家共同学习讨论 文章目录 【深度学习】【RKNN】【C】模型转化、环境搭建以及模型部署的详细教程前言模型转换--pytorch转rknnpytorch转onnxonnx转rkn…...

CentOS环境上离线安装python3及相关包
0. 准备操作系统及安装包 准备操作系统环境: 首先安装依赖包,安装相应的编译工具 [rootbigdatahost bin]# yum -y install zlib-devel bzip2-devel openssl-devel ncurses-devel sqlite-devel readline-devel tk-devel gdbm-devel db4-devel libpcap-d…...

学习threejs,使用设置bumpMap凹凸贴图创建褶皱,实现贴图厚度效果
👨⚕️ 主页: gis分享者 👨⚕️ 感谢各位大佬 点赞👍 收藏⭐ 留言📝 加关注✅! 👨⚕️ 收录于专栏:threejs gis工程师 文章目录 一、🍀前言1.1 ☘️THREE.MeshPhongMaterial高…...

React表单联动
Ant Design 1、dependencies Form.Item 可以通过 dependencies 属性,设置关联字段。当关联字段的值发生变化时,会触发校验与更新。 一种常见的场景:注册用户表单的“密码”与“确认密码”字段。“确认密码”校验依赖于“密码”字段&#x…...

408数据结构:栈、队列和数组选择题做题笔记
408数据结构 第一章 绪论 第二章 线性表 绪论、线性表选择题做题笔记 第三章 栈、队列和数组 栈、队列和数组选择题做题笔记 文章目录 408数据结构前言 一、队列二、栈和队列的应用总结 前言 本篇文章为针对王道25数据结构课后习题的栈、队列和数组的做题笔记,后续…...
sql工具!好用!爱用!
SQLynx的界面设计简洁明了,操作逻辑清晰易懂,没有复杂的图标和按钮,想对哪部分操作就在哪里点击右键,即使你是数据库小白也能轻松上手。 尽管SQLynx是一款免费的工具,但是它的功能却丝毫不逊色于其他付费产品ÿ…...

嵌入式驱动开发详解3(pinctrl和gpio子系统)
文章目录 前言pinctrl子系统pin引脚配置pinctrl驱动详解 gpio子系统gpio属性配置gpio子系统驱动gpio子系统API函数与gpio子系统相关的of函数 pinctrl和gpio子系统的使用设备树配置驱动层部分用户层部分 前言 如果不用pinctrl和gpio子系统的话,我们开发驱动时需要先…...
:IO类)
【C++】IO库(一):IO类
IO 库 C 不直接处理输入输出,而是通过定义一族定义在标准库当中的类型来处理IO。 8.1 IO 类 为了支持不同种类的 IO 处理操作,除了 istream 和 ostream 之外,标准库还定义了其它 IO 类型。这些类型分别定义在三个独立的头文件当中…...

uniapp介入极光推送教程 超级详细
直接按照下面教程操作 一步一步来 很快就能 完成 下面的文章非常详细 ,我就不班门弄斧了 直接上原文链接 https://blog.csdn.net/weixin_52830464/article/details/143823231...

阿里云整理(一)
阿里云整理 1. 介绍规模 2. 专业名词2.1 专有网络VPC2.2 安全组SG2.3 云服务器ECS2.4 资源组2.5 部署集2.5 web测试 1. 介绍 阿里云是一家提供云计算和人工智能服务的科技公司,成立于2009年,总部位于杭州。它为全球客户提供全方位的云服务ÿ…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...
