leetcode:222完全二叉树的节点个数
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2h 个节点。
示例 1:

输入:root = [1,2,3,4,5,6]
输出:6
示例 2:
输入:root = []
输出:0
示例 3:
输入:root = [1]
输出:1
提示:
树中节点的数目范围是[0, 5 * 104]
0 <= Node.val <= 5 * 104
题目数据保证输入的树是 完全二叉树
进阶:遍历树来统计节点是一种时间复杂度为 O(n) 的简单解决方案。你可以设计一个更快的算法吗?
步骤1:题目分析
问题性质:
本问题要求计算给定完全二叉树的节点数。
输入条件:
- 树的根节点
root。 - 树是完全二叉树(完全二叉树定义见题目)。
输出条件:
- 返回完全二叉树的节点个数。
限制条件:
- 树中节点的范围是
[0, 5 * 10^4]。 - 节点值范围是
[0, 5 * 10^4]。 - 完全二叉树性质:
- 除了最底层,其余层的节点数达到最大值。
- 最底层节点集中在最左侧。
边界条件:
- 树为空(
root = [])。 - 树只有一个节点。
- 树的最底层部分节点缺失,但仍满足完全二叉树性质。
步骤2:解题思路
方法1:朴素解法(时间复杂度 O(n))
- 思想:遍历整个树,统计所有节点数量。
- 实现方式:使用递归或迭代方式实现树的遍历。
- 时间复杂度:O(n),因为需要访问每个节点。
- 缺点:没有利用完全二叉树的性质优化。
方法2:利用完全二叉树性质(时间复杂度 O(log²n))
- 思想:完全二叉树的性质可以帮助我们快速计算节点个数:
- 若树是满二叉树(所有节点都填满),节点总数为
2^h - 1,其中h是树的深度。 - 如果树不是满二叉树,可以递归地判断左右子树:
- 通过计算左右子树的高度,判断左子树是否是满二叉树:
- 若左子树高度等于右子树高度,则左子树为满二叉树,节点数为
2^h - 1。 - 否则,递归到右子树进行计算。
- 若左子树高度等于右子树高度,则左子树为满二叉树,节点数为
- 通过计算左右子树的高度,判断左子树是否是满二叉树:
- 若树是满二叉树(所有节点都填满),节点总数为
- 时间复杂度:
- 对于完全二叉树,树的深度为 O(logn),递归每次减少一半的节点。
- 每次递归需要计算树的高度(O(logn))。
- 总时间复杂度:O(log²n)。
- 空间复杂度:O(logn)(递归栈深度)。
步骤3:C++代码实现

代码注释说明:
computeDepth函数:- 计算完全二叉树的深度,只需沿着左子树遍历即可,时间复杂度 O(logn)。
countNodes函数:- 递归判断左右子树是否为满二叉树。
- 若是满二叉树,直接通过公式计算节点数量,无需遍历。
- 若不是,递归到子树继续判断。
步骤4:解决问题的启发
- 利用特定数据结构的性质:
- 本题通过完全二叉树的特殊性质大幅优化节点统计效率。设计高效算法时,理解数据结构的特性是关键。
- 数学与递归的结合:
- 使用数学公式(满二叉树节点数公式)结合递归分治法,解决问题的效率远高于直接遍历。
- 时间复杂度的改进:
- 从 O(n) 优化到 O(log²n),体现了算法优化的重要性。
步骤5:算法在实际生活中的应用
实际应用场景:数据库索引结构
完全二叉树的性质和节点统计方法可用于数据库索引优化:
- 场景:
- 数据库的 B+ 树索引结构中,节点数量可以通过类似的递归计算方法快速统计。
- 例如,统计某个范围内的数据条目数量。
- 实现方法:
- 利用 B+ 树的分层结构和满二叉树性质,通过计算左子树和右子树的深度快速确定数据范围的节点数量。
实际示例:文件系统节点统计
文件系统中,完全二叉树常用于模拟目录和文件的结构。计算某个子目录下的文件总数时,可以采用类似的递归计算方法,快速得出结果,而无需遍历整个目录结构。
相关文章:

leetcode:222完全二叉树的节点个数
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。 完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最…...

[STM32]从零开始的STM32 FreeRTOS移植教程
一、前言 如果能看到这个教程的话,说明大家已经学习嵌入式有一段时间了。还记得嵌入式在大多数时候指的是什么吗?是的,我们所说的学习嵌入式大部分时候都是在学习嵌入式操作系统。从简单的一些任务状态机再到复杂一些的RTOS,再到最…...

java——Tomcat连接池配置NIO、BIO、APR
Tomcat连接池的配置涉及不同的IO模型,包括NIO(Non-blocking IO,非阻塞IO)、APR(Apache Portable Runtime,Apache可移植运行库)和BIO(Blocking IO,阻塞IO)。以…...

跨域相关的一些问题 ✅
当网页从一个源(https://baidu.com)请求另一个源(如 https://taobao/api)的资源时,就发生了跨域。由于安全原因(防止恶意网站通过脚本访问用户在其他网站上的数据),浏览器对跨域请求…...

RPC学习
一、什么是 RPC RPC(Remote Procedure Call),即远程过程调用,是一种计算机通信协议,它允许运行在一台计算机上的程序调用另一台计算机上的子程序或函数,就好像调用本地程序中的函数一样,无需程序…...
)
coe文件转mif(c语言)
1 mif文件格式 DEPTH=1024; --The size of data in bits WIDTH=16; --The size of memory in words ADDRESS_RADIX = DEC; --The radix for address values DATA_RADIX = UNS...

【leetcode】动态规划
31. 873. 最长的斐波那契子序列的长度 题目: 如果序列 X_1, X_2, ..., X_n 满足下列条件,就说它是 斐波那契式 的: n > 3对于所有 i 2 < n,都有 X_i X_{i1} X_{i2} 给定一个严格递增的正整数数组形成序列 arr ࿰…...
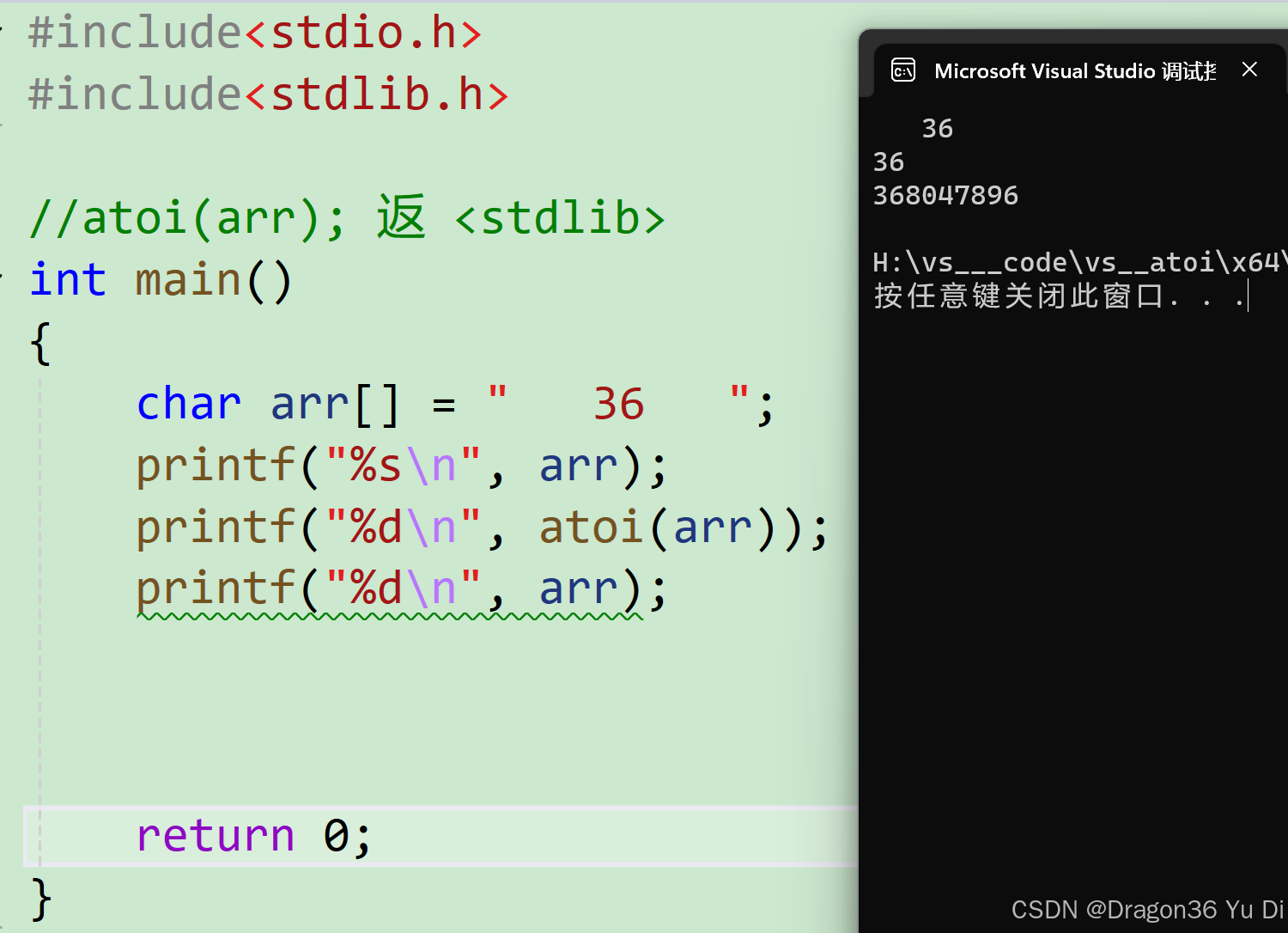
介绍一下atoi(arr);(c基础)
hi , I am 36 适合对象c语言初学者 atoi(arr);是返回整数(int型),整数是arr数组中字符中数字 格式 #include<stdio.h> atoi(arr); 返回值arr数组中的数字 未改变arr数组 #include<stdlib.h>//atoi(arr); 返 <stdlib> int main(…...

docker入门学习笔记
docker的定义 docker是一个用于构建、运行、传送 应用程序的平台。 为什么要使用docker ? 在开发测试库环境中测试成功后,打包成集装箱,到生产环境也是能够成功的。而传统的安装方式不仅繁琐,并且在测试环境安装后,到…...

使用Python和Pybind11调用C++程序(CMake编译)
目录 一、前言二、安装 pybind11三、编写C示例代码四、结合Pybind11和CMake编译C工程五、Python调用动态库六、参考 一、前言 跨语言调用能对不同计算机语言进行互补,本博客主要介绍如何实现Python调用C语言编写的函数。 实验环境: Linux gnuPython3.10…...
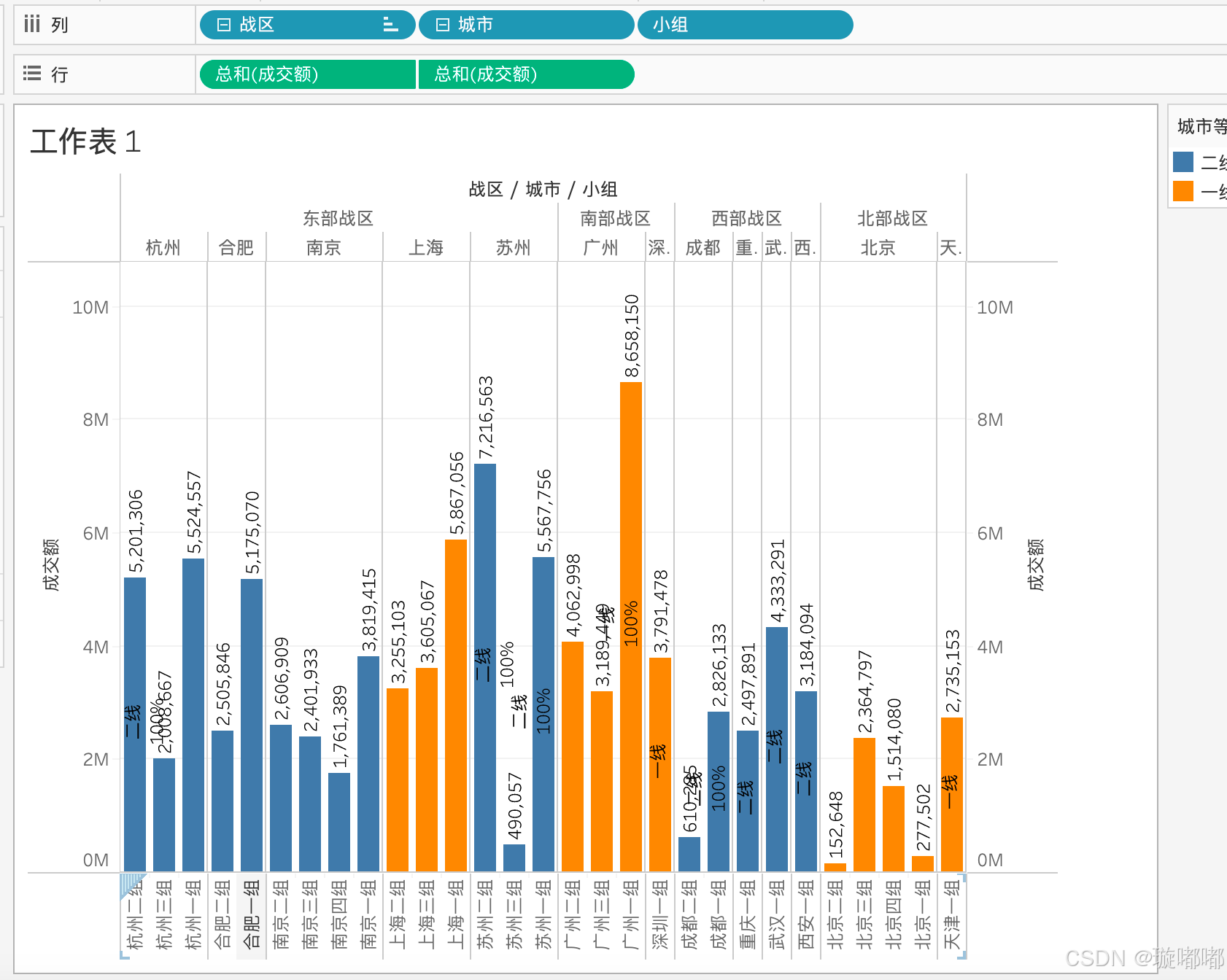
tableau-制作30个图表
制作条形图 步骤: 1、横轴是数值,对应了某一个度量值,纵轴是一个标签 战区的成交额,条形图横轴是战区,纵轴是成交额 下钻条形图 1、增加业务架构-战区右键点击,分层结构,增加分层结构 调整业务架构,将战区,城市,小组移动到业务架构下方 此时的条形图上方有➕号展开后…...

2024APMCM亚太杯数学建模C题【宠物行业】原创论文分享
大家好呀,从发布赛题一直到现在,总算完成了2024 年APMCM亚太地区大学生数学建模竞赛C题的成品论文。 给大家看一下目录吧: 目录 摘 要: 10 一、问题重述 14 二.问题分析 15 2.1问题一 15 2.2问题二 15 2.3问题三…...
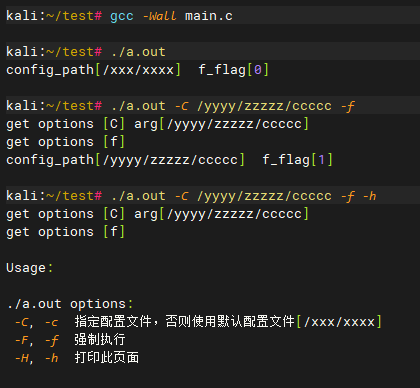
C语言解析命令行参数
原文地址:C语言解析命令行参数 – 无敌牛 欢迎参观我的个人博客:无敌牛 – 技术/著作/典籍/分享等 C语言有一个 getopt 函数,可以对命令行进行解析,下面给出一个示例,用的时候可以直接copy过去修改,很方便…...
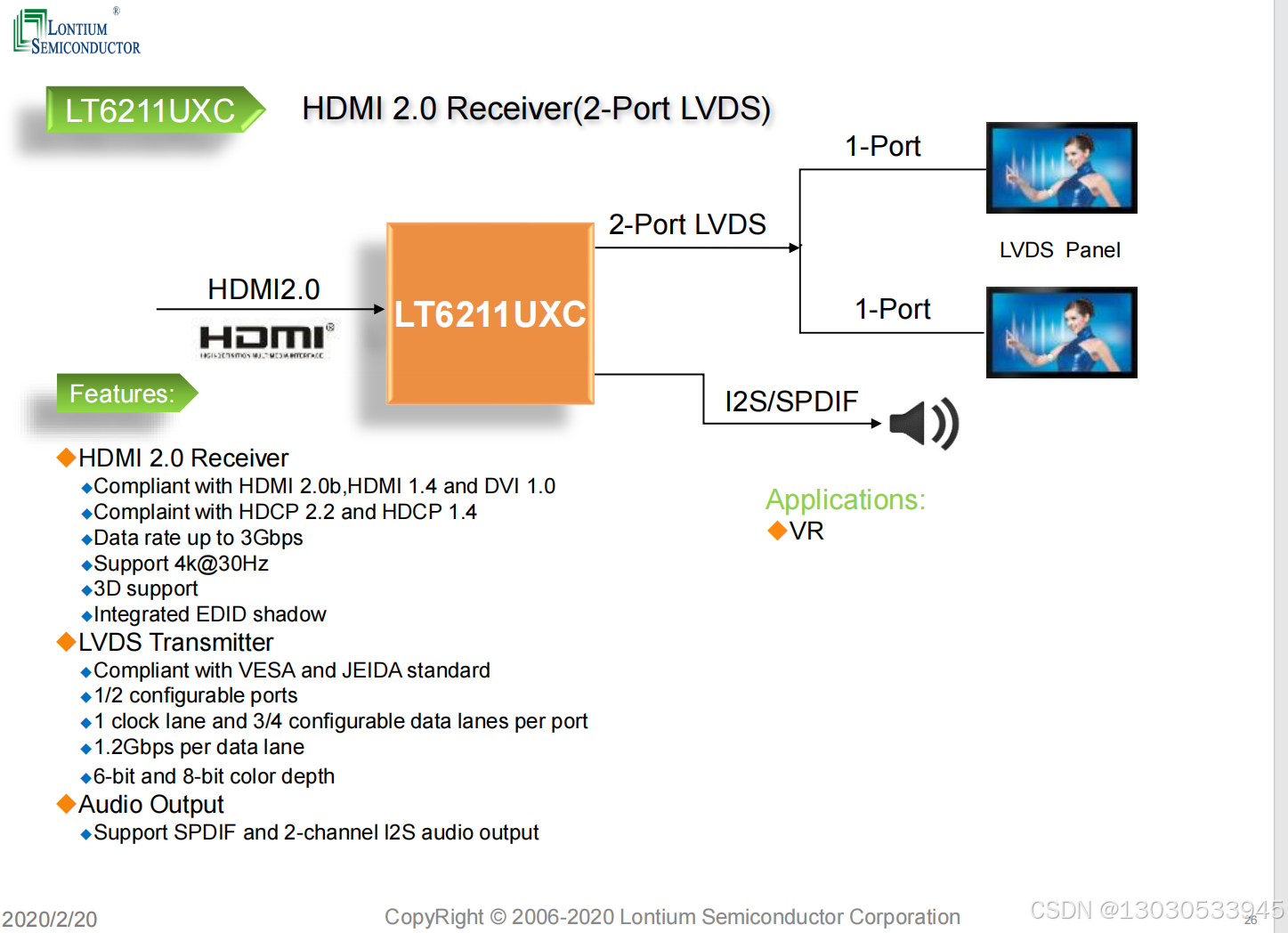
推荐一款龙迅HDMI2.0转LVDS芯片 LT6211UX LT6211UXC
龙迅的HDMI2.0转LVDS芯片LT6211UX和LT6211UXC是两款高性能的转换器芯片,它们在功能和应用上有所差异,同时也存在一些共同点。以下是对这两款芯片的详细比较和分析: 一、LT6211UX 主要特性: HDMI2.0至LVDS和MIPI转换器。HDMI2.0输…...
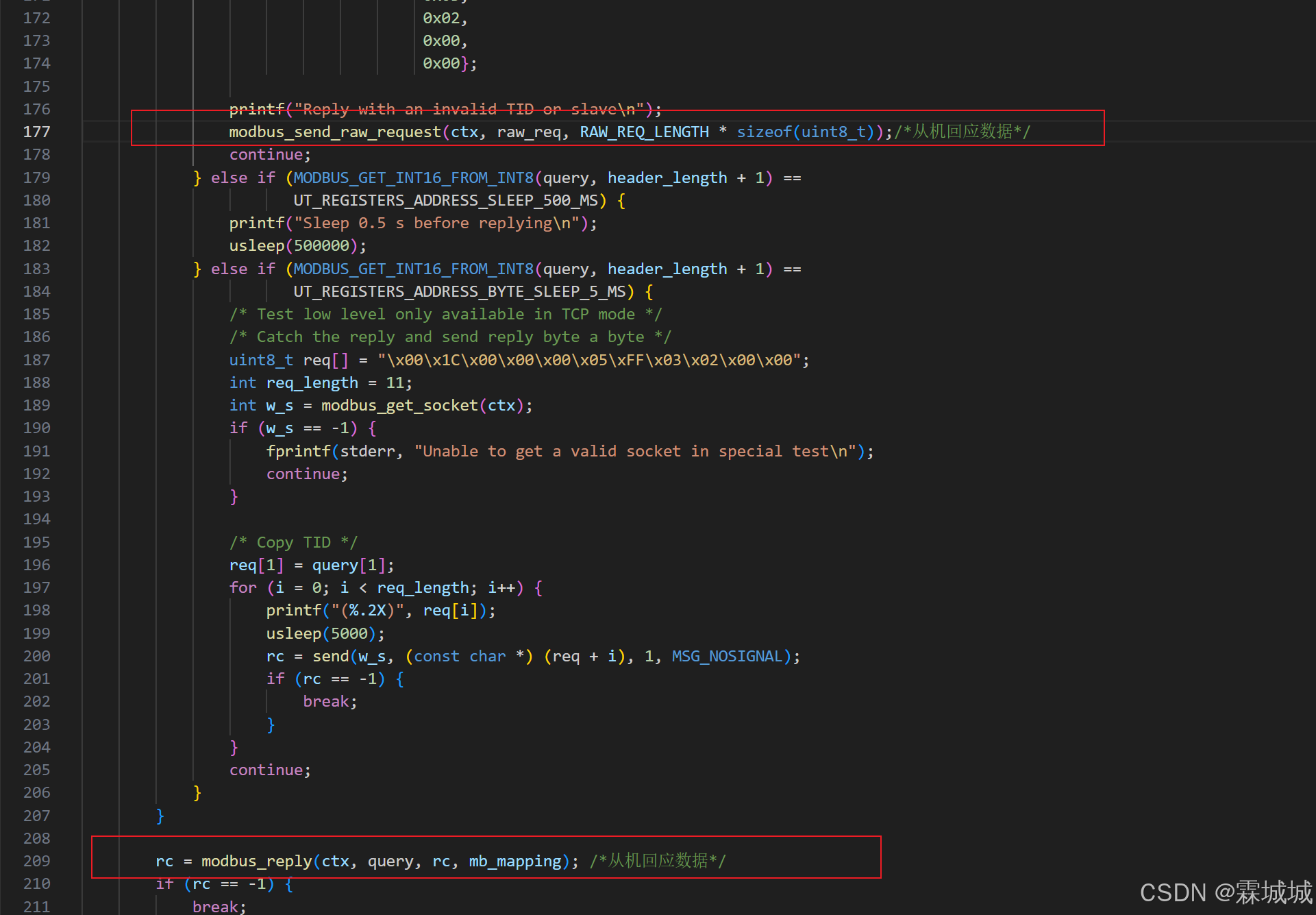
libmodbus 源码学习笔记
1.核心函数_框架_数据结构 整个通信的过程 就是上面这个框架 下面就是具体过程 <1> 主设备 我们首先要初始化 我们要使用的串口 然后 设置我们要访问的哪一个设备 最后打开串口 <2>从机设备 也是我们要初始化我们的串口 然后随后立即设置我们的串口设备地址 最后…...
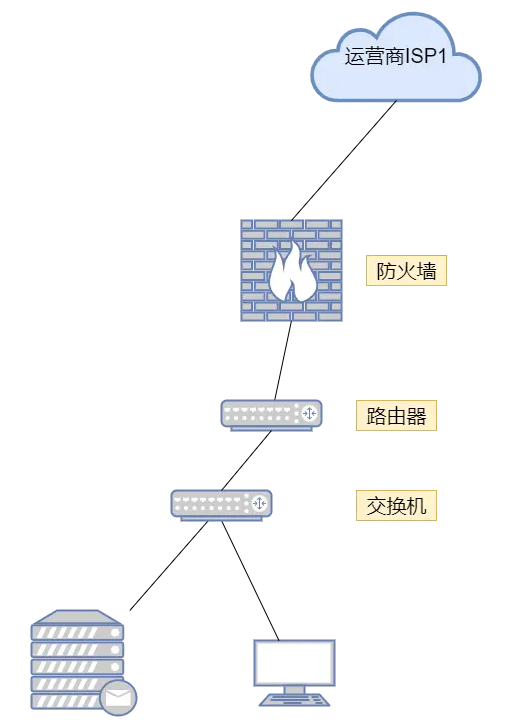
通用网络安全设备之【防火墙】
概念: 防火墙(Firewall),也称防护墙,它是一种位于内部网络与外部网络之间的网络安全防护系统,是一种隔离技术,允许或是限制传输的数据通过。 基于 TCP/IP 协议,主要分为主机型防火…...

Vue.js基础——贼简单易懂!!(响应式 ref 和 reactive、v-on、v-show 和 v-if、v-for、v-bind)
Vue.js是一个渐进式JavaScript框架,用于构建用户界面。它专门设计用于Web应用程序,并专注于视图层。Vue允许开发人员创建可重用的组件,并轻松管理状态和数据绑定。它还提供了一个虚拟DOM系统,用于高效地渲染和重新渲染组件。Vue以…...
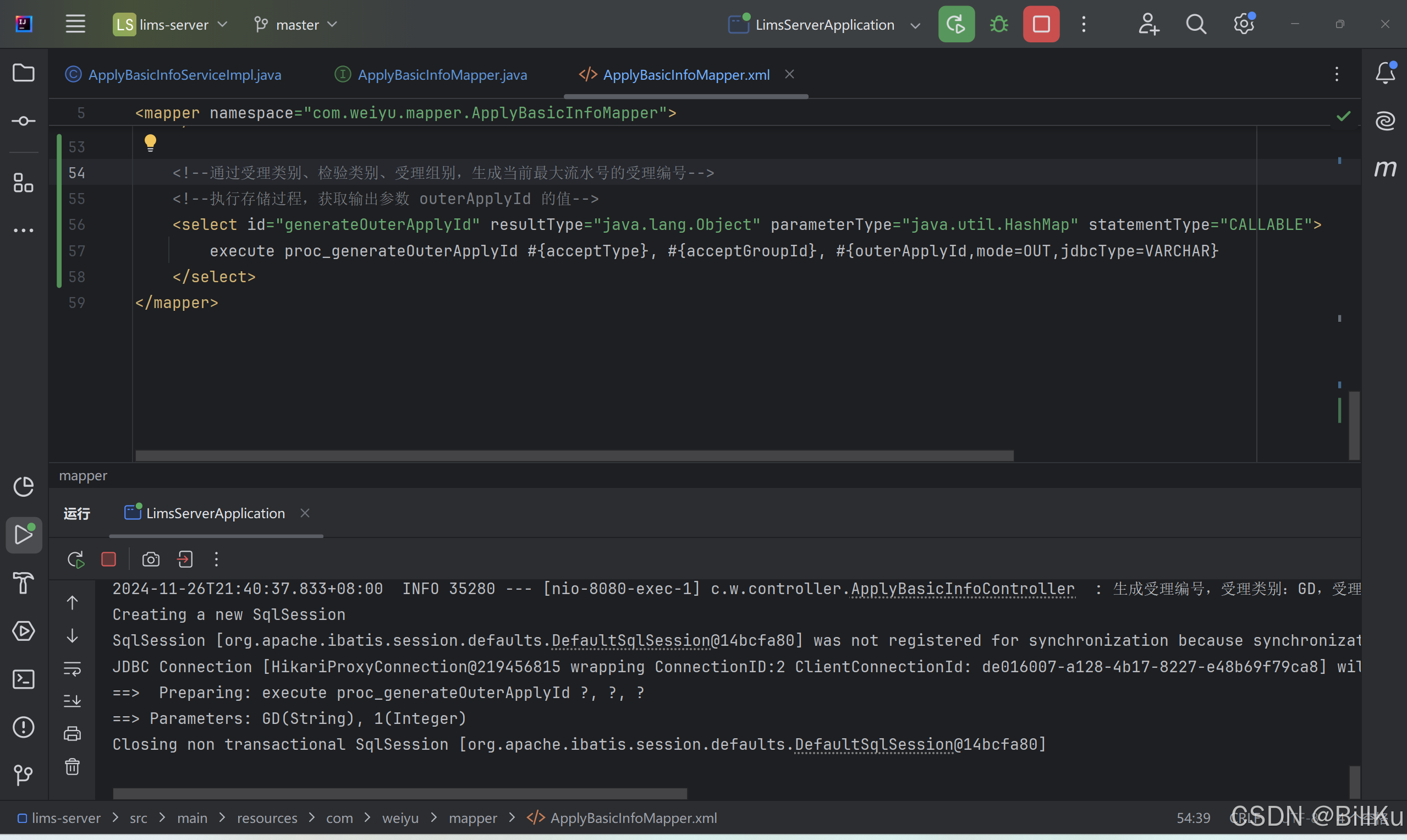
Mybatis 执行存储过程,获取输出参数的值
数据库环境:SQL Server 2008 R2 存储过程 alter procedure proc_generateOuterApplyId acceptType varchar(4),acceptGroupId int,outerApplyId varchar(20) output as begin set nocount onset outerApplyId 24GD6688--select outerApplyId as …...
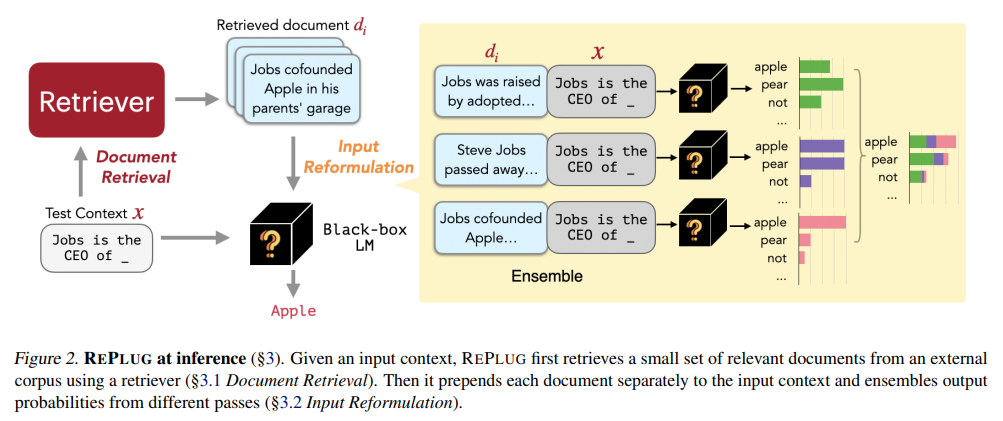
RAG架构类型
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...
Oracle 数据库 IDENTITY 列的性能选项
在上一篇文章Oracle 数据库 IDENTITY 列中,我们介绍了Oracle IDENTITY列的基础知识。本文将介绍IDENTITY列的几个性能选项。由于IDENTITY列内部使用sequence机制,因此也等同于是sequence的性能选项。 由于sequence是递增的,在高并发时&#…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...
