每天五分钟机器学习:支持向量机数学基础之超平面分离定理
本文重点
超平面分离定理(Separating Hyperplane Theorem)是数学和机器学习领域中的一个重要概念,特别是在凸集理论和最优化理论中有着广泛的应用。该定理表明,在特定的条件下,两个不相交的凸集总可以用一个超平面进行分离。
定义与表述
超平面分离定理(Separating Hyperplane Theorem)又称凸集分离定理,其表述如下:

定义:若C和D为非空凸集,且C ∩ D = ∅,则存在非零向量a和常数b,使得对于所有x ∈ C,有a^T x ≤ b,对于所有x ∈ D,有a^T x ≥ b。也即,存在一个超平面{ x | a^T x = b }将C和D分离。

这个定理的核心在于,两个不相交的凸集总可以找到一个超平面,使得这两个集合分别位于超平面的两侧。
所以根据超平面分离定
相关文章:

每天五分钟机器学习:支持向量机数学基础之超平面分离定理
本文重点 超平面分离定理(Separating Hyperplane Theorem)是数学和机器学习领域中的一个重要概念,特别是在凸集理论和最优化理论中有着广泛的应用。该定理表明,在特定的条件下,两个不相交的凸集总可以用一个超平面进行分离。 定义与表述 超平面分离定理(Separating Hy…...

TCP/IP网络协议栈
TCP/IP网络协议栈是一个分层的网络模型,用于在互联网和其他网络中传输数据。它由几个关键的协议层组成,每一层负责特定的功能。以下是对TCP/IP协议栈的简要介绍: TCP/IP协议模型的分层 1. 应用层(Application Layer)…...

利用编程思维做题之最小堆选出最大的前10个整数
1. 理解问题 我们需要设计一个程序,读取 80,000 个无序的整数,并将它们存储在顺序表(数组)中。然后从这些整数中选出最大的前 10 个整数,并打印它们。要求我们使用时间复杂度最低的算法。 由于数据量很大,直…...

详解MVC架构与三层架构以及DO、VO、DTO、BO、PO | SpringBoot基础概念
🙋大家好!我是毛毛张! 🌈个人首页: 神马都会亿点点的毛毛张 今天毛毛张分享的是SpeingBoot框架学习中的一些基础概念性的东西:MVC结构、三层架构、POJO、Entity、PO、VO、DO、BO、DTO、DAO 文章目录 1.架构1.1 基本…...

Unity C# 影响性能的坑点
c用的时间长了怕unity的坑忘了,记录一下。 GetComponent最好使用GetComponent<T>()的形式, 继承自Monobehaviour的函数要避免空的Awake()、Start()、Update()、FixedUpdate().这些空回调会造成性能浪费 GetComponent方法最好避免在Update当中使用…...

工作学习:切换git账号
概括 最近工作用的git账号下发下来了,需要切换一下使用的账号。因为是第一次弄,不熟悉,现在记录一下。 打开设置 路径–git—git remotes,我这里选择项是Manage Remotes,点进去就可以了。 之后会出现一个输入框&am…...
)
量化交易系统开发-实时行情自动化交易-8.量化交易服务平台(一)
19年创业做过一年的量化交易但没有成功,作为交易系统的开发人员积累了一些经验,最近想重新研究交易系统,一边整理一边写出来一些思考供大家参考,也希望跟做量化的朋友有更多的交流和合作。 接下来会对于收集整理的33个量化交易服…...

Scala习题
姓名,语文,数学,英语 张伟,87,92,88 李娜,90,85,95 王强,78,90,82 赵敏,92,88,91 孙涛,…...

结构方程模型(SEM)入门到精通:lavaan VS piecewiseSEM、全局估计/局域估计;潜变量分析、复合变量分析、贝叶斯SEM在生态学领域应用
目录 第一章 夯实基础 R/Rstudio简介及入门 第二章 结构方程模型(SEM)介绍 第三章 R语言SEM分析入门:lavaan VS piecewiseSEM 第四章 SEM全局估计(lavaan)在生态学领域高阶应用 第五章 SEM潜变量分析在生态学领域…...

OpenCV图像基础处理:通道分离与灰度转换
在计算机视觉处理中,理解图像的颜色通道和灰度表示是非常重要的基础知识。今天我们通过Python和OpenCV来探索图像的基本组成。 ## 1. 图像的基本组成 在数字图像处理中,彩色图像通常由三个基本颜色通道组成: - 蓝色(Blue&#x…...

C++ 类和对象(类型转换、static成员)
目录 一、前言 二、正文 1.隐式类型转换 1.1隐式类型转换的使用 2.static成员 2.1 static 成员的使用 2.1.1static修辞成员变量 2.1.2 static修辞成员函数 三、结语 一、前言 大家好,我们又见面了。昨天我们已经分享了初始化列表:https://blog.c…...
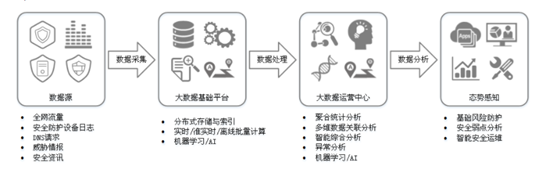
【网络安全设备系列】12、态势感知
0x00 定义: 态势感知(Situation Awareness,SA)能够检测出超过20大类的云上安全风险,包括DDoS攻击、暴力破解、Web攻击、后门木马、僵尸主机、异常行为、漏洞攻击、命令与控制等。利用大数据分析技术,态势感…...

Linux介绍与安装指南:从入门到精通
1. Linux简介 1.1 什么是Linux? Linux是一种基于Unix的操作系统,由Linus Torvalds于1991年首次发布。Linux的核心(Kernel)是开源的,允许任何人自由使用、修改和分发。Linux操作系统通常包括Linux内核、GNU工具集、图…...

BGE-M3模型结合Milvus向量数据库强强联合实现混合检索
在基于生成式人工智能的应用开发中,通过关键词或语义匹配的方式对用户提问意图进行识别是一个很重要的步骤,因为识别的精准与否会影响后续大语言模型能否检索出合适的内容作为推理的上下文信息(或选择合适的工具)以给出用户最符合…...
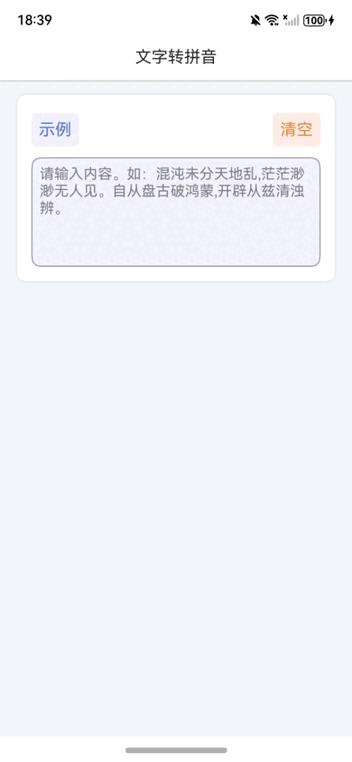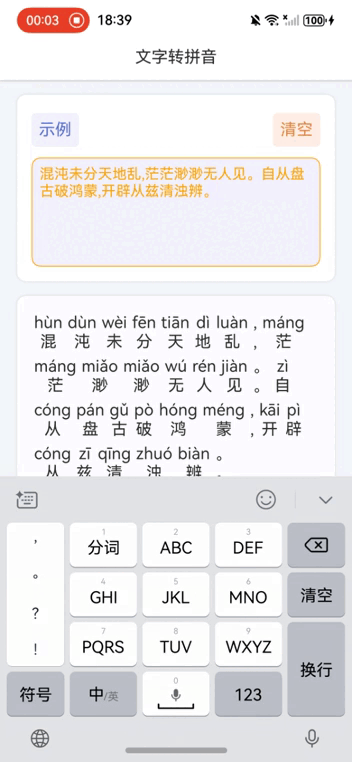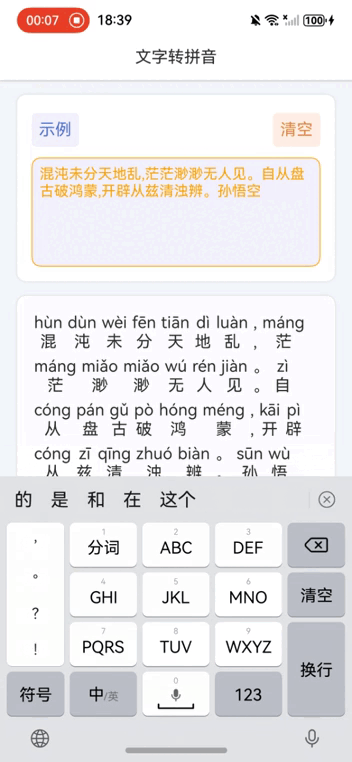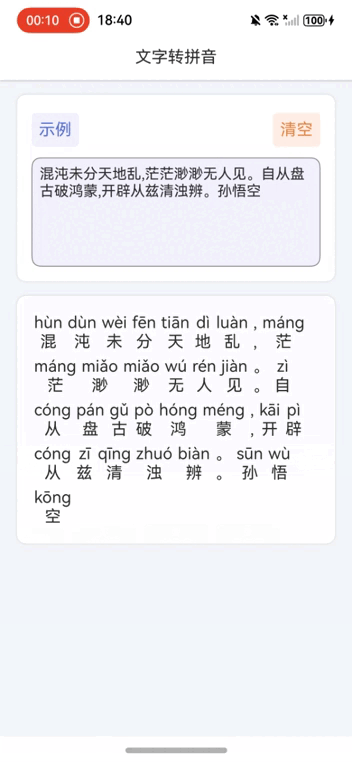
鸿蒙NEXT开发案例:文字转拼音
【引言】 在鸿蒙NEXT开发中,文字转拼音是一个常见的需求,本文将介绍如何利用鸿蒙系统和pinyin-pro库实现文字转拼音的功能。 【环境准备】 • 操作系统:Windows 10 • 开发工具:DevEco Studio NEXT Beta1 Build Version: 5.0.…...
)
CTF之密码学(栅栏加密)
栅栏密码是古典密码的一种,其原理是将一组要加密的明文划分为n个一组(n通常根据加密需求确定,且一般不会太大,以保证密码的复杂性和安全性),然后取每个组的第一个字符(有时也涉及取其他位置的字…...

修改插槽样式,el-input 插槽 append 的样式
需缩少插槽 append 的 宽度 方法1、使用内联样式直接修改,指定 width 为 30px <el-input v-model"props.applyBasicInfo.outerApplyId" :disabled"props.operateCommandType input-modify"><template #append><el-button click…...

UPLOAD LABS | PASS 01 - 绕过前端 JS 限制
关注这个靶场的其它相关笔记:UPLOAD LABS —— 靶场笔记合集-CSDN博客 0x01:过关流程 本关的目标是上传一个 WebShell 到目标服务器上,并成功访问: 我们直接尝试上传后缀为 .php 的一句话木马: 如上,靶场弹…...

【css实现收货地址下边的平行四边形彩色线条】
废话不多说,直接上代码: <div class"address-block" ><!-- 其他内容... --><div class"checked-ar"></div> </div> .address-block{height:120px;position: relative;overflow: hidden;width: 500p…...

缓存方案分享
不知道大家平常更新缓存是怎么做的,但是大部分时候都是更新数据的同时更新缓存,今天和同事一起聊到一个缓存方案的问题,感觉很有趣、非常精妙,记录一下。 基于此本文将介绍几种常见的缓存更新策略,包括简单的缓存覆盖…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...
