蓝桥杯c++算法秒杀【6】之动态规划【上】(数字三角形、砝码称重(背包问题)、括号序列、组合数问题:::非常典型的必刷例题!!!)
下将以括号序列、组合数问题超级吧难的题为例子讲解动态规划

别忘了请点个赞+收藏+关注支持一下博主喵!!!! ! ! ! !
关注博主,更多蓝桥杯nice题目静待更新:)
动态规划
一、数字三角形
【问题描述】
上图给出了一个数字三角形。从三角形的顶部到底部有很多条路径。对于每条路径, 把路径上面的数加起来可以得到一个和,你的任务就是找到最大的和。
路径上的每一步只能从一个数走到下一层和它最近的左边的那个数或者右边的那个 数。此外,向左下走的次数与向右下走的次数相差不能超过1。
【输入格式】
输入的第一行包含一个整数N(1⩽N⩽100),表示三角形的行数。
下面的N行给出数字三角形。数字三角形上的数都是0至100之间的整数。
【输出格式】
输出一个整数表示答案。
【样例输入】

【样例输出】
27
解析:
本题是十分经典的动态规划题。
为了方便存储与操作,可以将题目描述中的等腰三角形转换为直角三角形,如下图所示。

将其转换为直角三角形后,就可以用一个二维数组(a[][])来存储它。这样三角形第i行 的第j 个数字就可以通过a[i][j] 来表示。同时原来向左下走就变为了向下走,本题下文解析所说的“向下走”即为“向左下走”,向右下走还是向右下走。
在处理完样例输入后,我们来尝试对题目进行求解。
由于“向左下走的次数与向右下走的次数相差不能超过1”这个限制条件看上去比较复杂,所以我们可将该题分解为两个子问题: 第一个子问题是不考虑限制条件,只解决如何走的问题;第二个子问题是加上这个限制条件找到走到底部的最大路径和,从而完整解答出本题。对于每个子问题,都分别用DFS和动态规划两种方式来解题,大家可进一步体验这两种方式的特点。
解决子问题1:DFS模式
题目要求我们从三角形的顶部开始走,而顶部只有一个数字a[1][1],所以所走路径的起点一定是a[1][1]。
由于我们每一步只能向下走或者向右下走,因此a[1][1]的下一步只有以下两种可能。
(1)走向a[2][1]。
(2)走向a[2][2]。
具体要走向哪个呢?我们并不好确定。
我们能得知的是,如果设dfs(i,j) 表示从 a[i][j] 走到底部的最大路径和,那么我们一定会走向max(dfs(2,1),dfs(2,2)) 所对应的路径,即从 a[1][1] 走到底部的最大路径和:

在该式子中,dfs(1,1) 是我们要求解的,a[1][1] 是已知的,dfs(2,1)、dfs(2,2) 是未知的。 显然,只要存在未知数,就无法求解dfs(1,1)的值。因此,必须先求解dfs(2,1) 和dfs(2,2)。
但要怎么求解它们呢? 我们以求解dfs(i,j) 为例。
当a[i][j](i < n) 不在底部时,每一步只能向下走或者向右下走,因此a[i][j] 的下一步只有两种可能。
(1)走向a[i+1][j]。
(2)走向a[i+1][j +1]。 当a[i][j](i = n) 在底部时,我们将无法再走任何一步。 由此可得 :

参考代码如下 【时间复杂度为 O()】
#include <bits/stdc++.h>
using namespace std;const int N = 1e2 + 10;
int n, a[N][N];int dfs(int i, int j) {if (i == n) return a[i][j]; // 走到底部无法再走了,直接返回return max(dfs(i + 1, j), dfs(i + 1, j + 1)) + a[i][j];
}signed main() {cin >> n;for (int i = 1; i <= n; i++) {for (int j = 1; j <= i; j++) {cin >> a[i][j];}}cout << dfs(1, 1) << '\n';return 0;
} 在上方代码中,每次dfs都几乎调用了自己两次,所以代码的时间复杂度约为O()。
如果一个三角形的行数为4,则程序的递归过程将如下图所示。

显然,O() 的时间复杂度是十分低效的,无法帮助我们顺利解出本题。至于复杂度低效的原因,从上图中不难发现是因为在递归的过程中做了过多重复的计算,比如在上图中, dfs(3, 2) 就重复计算了一次。
那么,我们要如何避免递归时的重复计算呢?
可以采用一个简单且高效的方法——记忆化,即定义一个二维数组res[][],用res[i][j]保 存dfs(i,j) 的计算结果。当再次需要dfs(i,j) 的计算结果时,直接返回res[i][j] 即可,无须继续递归下去。
使用了记忆化的方法优化后,最多只需进行约次递归。
参考代码如下 【时间复杂度为 O()】
#include <bits/stdc++.h>
using namespace std;const int N = 1e2 + 10;
int n, a[N][N], res[N][N];int dfs(int i, int j) {if (res[i][j]) return res[i][j]; // 如果 res[i][j] 不为 0,说明已经计算过,直接返回结果if (i == n) return a[i][j]; // 到达底部,返回当前值return res[i][j] = max(dfs(i + 1, j), dfs(i + 1, j + 1)) + a[i][j]; // 计算并存储结果
}signed main() {cin >> n;for (int i = 1; i <= n; i++) {for (int j = 1; j <= i; j++) {cin >> a[i][j];}}cout << dfs(1, 1) << '\n';return 0;
}解决子问题1:动态规划模式
与DFS 不同的是,动态规划通常是采用递推的方式从上到下来求解问题。
在本题中,我们从三角形的顶部(1,1)走到三角形的某个位置(i,j)的方法颇多,根据不同的走法,所得到的路径和可能会有所差异。
由于本题需要求解的是从三角形顶部(1,1) 走到底部的最大路径和,所以在不同方法带 来的不同路径和中,我们只需要关注最大路径和即可。
于是,我们可以定义一个数组dp[][],其中dp[i][j] 用以表示从三角形顶部(11) 走到(ij) 的所有路径和中的最大值。
当走到底部时,所处的位置可能有(n,1)、(n,2)、...、(n,n),它们对应的最大路径和分 别为dp[n][1]、dp[n][2]、...、dp[n][n]。我们要的是这当中的最大路径和,即 ![]() 。
。
起初,处于三角形的顶部(1,1)。因为从(1,1) 走到(1,1) 的方法仅有一种,所以我们可 得dp[1][1] = a[1][1]。
(1)从位置(i−1,j) 向下走一步。
(2)从位置(i−1,j−1) 向右下走一步。
无论我们选择哪种,从(1,1) 到(i,j) 的路径与 (1,1) 到 (i−1,j) 或 (i−1,j−1) 的路径都只会有一步之差。所以两种方法到达(i,j)的最大路径和分别如下。
(1)dp[i−1][j]+a[i][j]。
(2)dp[i−1][j −1]+a[i][j]。
为了使到达位置(i,j) 的路径和最大,我们需要从这两种方法中选择较大的一种,即

这样,我们便完成了dp方程的转移。
参考代码如下 【时间复杂度为 O()】
#include <bits/stdc++.h>
using namespace std;const int N = 1e2 + 10;
int n, a[N][N], dp[N][N];signed main() {cin >> n;for (int i = 1; i <= n; i++) {for (int j = 1; j <= i; j++) {cin >> a[i][j];}}dp[1][1] = a[1][1];for (int i = 2; i <= n; i++) {for (int j = 1; j <= i; j++) {dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - 1]) + a[i][j];}}int ans = 0;for (int j = 1; j <= n; j++) {ans = max(ans, dp[n][j]);}cout << ans << '\n';return 0;
}提示: 以上情况都是在不考虑“向左下走的次数与向右下走的次数相差不能超过1”这个限制 条件下分析的,接下来我们来思考加上向左下走的次数与向右下走的次数相差不能超过1这个限制条件之后该如何处理,即解决子问题2。
为了方便读者理解,接下来我们分别用动态规划和DFS两种方法对本题进行讲解。
解决子问题2:动态规划模式
我们可以采用最简单的方法:从顶部向底部走的过程中,额外添加一个状态——向下走 的次数,即定义dp[i][j][k]表示从(1,1)走到(i,j)一共向下走了k次的最大和。
根据向下走和向右下走的次数相差不能超过1的条件,那么从第1行到第n行一共要走 n−1步,由此可得:
•当n−1为奇数(n为偶数)时,向下走的次数可以为 ,也可以为
+1;
•当n−1为偶数(n为奇数)时,向下走的次数只能为 。
那么答案就可表示为:

对于位置(i,j),它可以由位置 (i − 1,j) 向下走了一步得到,也可以由位置(i−1,j−1) 向右下走了一步得到,于是dp转移方程为

参考代码如下【时间复杂度为O()】
#include <bits/stdc++.h>
using namespace std;const int N = 1e2 + 10;
int n, a[N][N], dp[N][N][N];signed main() {memset(dp, -0x3f, sizeof(dp)); // 某些情况可能并不存在,如 dp[2][1][0]:走到位置 (2,1) 时共向下走了 0 次。为了防止这种情况被转移,需初始化 dp 数组cin >> n;for (int i = 1; i <= n; i++) {for (int j = 1; j <= i; j++) {cin >> a[i][j];}}dp[1][1][0] = a[1][1];for (int i = 2; i <= n; i++) {for (int j = 1; j <= i; j++) {for (int k = 0; k <= (n - 1); k++) {if (!k) {dp[i][j][k] = dp[i - 1][j - 1][k] + a[i][j];} else {dp[i][j][k] = max(dp[i - 1][j - 1][k], dp[i - 1][j][k - 1]) + a[i][j];}}}}int ma = 0;if ((n - 1) & 1) {for (int j = 1; j <= n; j++) {ma = max(ma, max(dp[n][j][(n - 1) / 2], dp[n][j][(n - 1) / 2 + 1]));}} else {for (int j = 1; j <= n; j++) {ma = max(ma, dp[n][j][(n - 1) / 2]);}}cout << ma << '\n';return 0;
}虽说运用上述的方法已经可以完成本题了,但我们其实不额外添加一个状态也可以解决。 由上可得以下结论。
•当n−1为奇数(n为偶数)时,向下走的次数可以为 ,也可以为
+1;
•当n−1为偶数(n为奇数)时,向下走的次数只能为 。
基于向下走的次数、向右下走的次数限制不难发现以下情况。
•当n−1为奇数(n为偶数)时,无论中间的路线是什么样的,最后的位置只有两种可能:
( n , 1 + ),( n , 1 +
+ 1 )。
•当n为偶数时,无论中间的路线是什么样的,最后的位置只有一种可能:
( n , 1 + )。
所以我们并不需要考虑从顶部走到底部时向下走的次数,只需要保证最后的位置正确即可。

用dp[i][j]表示从(1,1)走到(i,j)的最大和并对其进行转移,那么答案就可以表示为:

参考代码如下【时间复杂度为O()】
#include <bits/stdc++.h>
using namespace std;const int N = 1e2 + 10;
int n, a[N][N], dp[N][N];signed main() {cin >> n;for (int i = 1; i <= n; i++) {for (int j = 1; j <= i; j++) {cin >> a[i][j];}}dp[1][1] = a[1][1];for (int i = 2; i <= n; i++) {for (int j = 1; j <= i; j++) {dp[i][j] = max(dp[i - 1][j - 1], dp[i - 1][j]) + a[i][j];}}// 根据 n-1 的奇偶性输出:在满足向下走的次数与向右下走的次数相差不能超过 1 的条件下可能会到达的位置对应的 dp 值if ((n - 1) & 1) {cout << max(dp[n][1 + (n - 1) / 2], dp[n][1 + (n - 1) / 2 + 1]) << '\n';} else {cout << dp[n][1 + (n - 1) / 2] << '\n';}return 0;
}解决子问题2:DFS模式
DFS的处理方法和动态规划的类似,有以下两种方法:
(1)额外添加一个状态使得答案满足条件;
(2)保证最后的位置正确使得答案满足条件。
下面给出第二种方法的参考代码。
参考代码如下
#include <bits/stdc++.h>
using namespace std;const int N = 1e2 + 10;
int n, a[N][N], res[N][N];int dfs(int i, int j) {if (res[i][j]) return res[i][j]; // 如果 res[i][j] 不为 0,说明已经计算过,直接返回结果if (i == n) {if (n % 2 && j == n / 2 + 1) return a[i][j]; // n 为奇数且 j 为中间位置if (n % 2 == 0 && (j == n / 2 || j == n / 2 + 1)) return a[i][j]; // n 为偶数且 j 为中间两个位置之一return -10000000; // 位置不正确时,返回一个极大的负数}return res[i][j] = max(dfs(i + 1, j), dfs(i + 1, j + 1)) + a[i][j]; // 计算并存储结果
}signed main() {cin >> n;for (int i = 1; i <= n; i++) {for (int j = 1; j <= i; j++) {cin >> a[i][j];}}cout << dfs(1, 1) << '\n';return 0;
}二、砝码称重
【问题描述】
你有一架天平和N个砝码,这N个砝码重量依次是W1,W2,...,WN。
请你计算一共可以称出多少种不同的重量。注意砝码可以放在天平两边。
【输入格式】
输入的第一行包含一个整数N。
第二行包含N个整数:W1,W2,W3,...,WN。
【输出格式】
输出一个整数表示答案。
【样例输入】
![]()
【样例输出】
10
【样例说明】

【评测用例规模与规定】
对于50% 的评测用例,1⩽ N ⩽15。
对于所有评测用例,1⩽ N ⩽100,N 个砝码总重不超过100000。
解析:
本题是道有限制的选择问题、背包问题的变形题。
在本题中,题目给定了1个天平及n个砝码,每个砝码都有自己的重量。天平存在以下 3 种状态。
(1)平衡。
(2)向左倾斜。
(3)向右倾斜。
这3种状态分别可称出的重量:
(1)0(忽略不计);
(2)左侧的砝码重量−右侧的砝码重量;
(3)右侧的砝码重量−左侧的砝码重量。
显然,天平的状态只会受到两侧砝码的重量影响。对于每个砝码,它都有以下3种处理方式。
(1)放在天平的左侧。
(2)放在天平的右侧。
(3)两侧都不放。
那么,n个砝码就有3n种处理方式(情况)。
在50%的评测用例中,1⩽n⩽15。当n=15时,315=14348907,数据规模为107 左右。
因此,我们可以使用直接dfs“暴力”搜索出放置n个砝码的所有情况,并统计这些情况能够称出的不同重量的个数。
(1)dfs“暴力”搜索
参考代码如下【时间复杂度为O()】
#include <bits/stdc++.h>
using namespace std;const int N = 1e2 + 10, M = 1e5 + 10;
int n, ans, w[N], vis[M]; // vis[x] = 1 表示可以称出重量 xvoid dfs(int i, int left, int right) {if (i > n) {vis[max(left, right) - min(left, right)] = 1;return;}// 将第 i 个砝码放置在左边dfs(i + 1, left + w[i], right);// 将第 i 个砝码放置在右边dfs(i + 1, left, right + w[i]);// 两边都不放dfs(i + 1, left, right);
}signed main() {cin >> n;for (int i = 1; i <= n; i++) {cin >> w[i];}dfs(1, 0, 0);for (int i = 1; i < M; i++) {if (vis[i]) {ans++;}}cout << ans << '\n';return 0;
} 可当 1 ⩽ n ⩽100 时,还能用dfs搜索出所有情况吗?显然不行,因为当n=100时, 会是个天文数字,计算机在有限的时间内是不可能搜索出所有情况的。
那怎么办呢? 考虑用动态规划解决。
(2)动态规划【正解】
1. 设计状态数组
按照常规的步骤,我们会设计一个状态数组dp[],其中dp[i]表示用前i个砝码所能称出 的不同重量的个数。
这么设计看似合理,答案也可以用dp[n] 轻松表示,但略加思考后不难发现其存在一个 致命问题,即在状态转移的过程中,无法处理相同的重量被重复计算的情况。
如何解决这个致命问题呢?我们只要将重量也设计在状态数组中,即设计一个boolean类 型的二维数组dp[][],其中 dp[i][j] = true 表示前 i 个砝码能通过天平称出重量 j,dp[i][j]= false 则表示前 i 个砝码不能通过天平称出重量j。
由于n个砝码的总重量不超过100000,所以我们只要在求解完整个数组后,枚举dp[n][1∼ 100000],统计其中值为 true 的元素个数,即可得出 n 个砝码所能称出的不同重量的个数。
到这里貌似没有什么问题。那么接下来,我们就来讨论一下如何求解dp[][]数组。
2. 初始状态
起初,我们未在天平两侧放置任何砝码,天平它会处于一种平衡的状态。我们可以认为 此时天平称的重量为0,即dp[0][0]=true。
3. 推导转移方程
事实上,天平所称出的重量总是会由重的一侧减去轻的一侧,即对于第i个砝码,若我 们将其放入天平较重的一侧,则它将使天平称出的重量增加wi;若将该砝码放入天平较轻的 一侧,则它将使天平称出的重量减少wi。例如,在我们处理完前i−1个砝码后,天平所称 出的重量为j,那么在处理完第i个砝码后,天平所能称出的重量将会根据对第i个砝码不 同的处理方式得到3种不同结果分别如下。
(1)j+wi:将第i 个砝码放在较重的一侧。
(2)j−wi:将第i 个砝码放在较轻的一侧。
(3)j:两侧都不放。 因此,我们可推导出以下3种状态转移式:
因此,我们可推导出以下3种状态转移式:

若将3个状态转移式整合成一个,可得
![]()
完成状态转移式的推导。 值得注意的是,在进行状态转移的过程中,可能会出现 j < w[i] 的情况( j - w[i] < 0 )。若不进行处理,就会导致数组的越界,进而导致答案错误。
因此,我们可以为所有重量添加一个偏移量offset(对于重量x,用x+offset来表示它), 如下图所示,使得∀j−w[i]+offset⩾0。
提示:添加上offset 后,dp[i][j] 的含义为前 i 个砝码能否通过天平称出重量 j−offset。

参考代码如下【时间复杂度为 O(n× n ∑ i=1 wi)】
#include <bits/stdc++.h>
using namespace std;const int N = 1e2 + 10, M = 1e5 + 10, offset = 1e5;
int n, ans, w[N], dp[N][2 * M];signed main() {cin >> n;for (int i = 1; i <= n; i++) {cin >> w[i];}dp[0][0 + offset] = true;for (int i = 1; i <= n; i++) {for (int j = 0; j < M + offset; j++) {if (j - w[i] >= 0) dp[i][j] |= dp[i - 1][j - w[i]];dp[i][j] |= dp[i - 1][j + w[i]] | dp[i - 1][j];}}for (int i = 1 + offset; i < M + offset; i++) {if (dp[n][i]) ans++;}cout << ans << '\n';return 0;
}。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。
下将以括号序列、组合数问题超级吧难的题为例子讲解动态规划
别忘了请点个赞+收藏+关注支持一下博主喵!!!! ! ! !
关注博主,更多蓝桥杯nice题目静待更新:)
相关文章:

蓝桥杯c++算法秒杀【6】之动态规划【上】(数字三角形、砝码称重(背包问题)、括号序列、组合数问题:::非常典型的必刷例题!!!)
下将以括号序列、组合数问题超级吧难的题为例子讲解动态规划 别忘了请点个赞收藏关注支持一下博主喵!!!! ! ! ! ! 关注博主,更多蓝桥杯nice题目静待更新:) 动态规划 一、数字三角形 【问题描述】 上图给出了…...

【Qt】重写QComboBox下拉展示多列数据
需求 点击QComboBox时,下拉列表以多行多列的表格展示出来。 实现 直接上代码: #include <QComboBox> #include <QTableWidget> #include <QVBoxLayout> #include <QWidget> #include <QEvent> #include <QMouseEve…...
【mac】终端左边太长处理,自定义显示名称(terminal路径显示特别长)
1、打开终端 2、步骤 (1)修改~/.zshrc文件 nano ~/.zshrc(2)添加或修改PS1,我是自定义了名字为“macminiPro” export PS1"macminiPro$ "(3)使用 nano: Ctrl o (字母…...

基于Springboot的流浪宠物管理系统
基于javaweb的流浪宠物管理系统 介绍 基于javaweb的流浪宠物管理系统的设计与实现,后端框架使用Springbootmybatis,前端框架使用Vuehrml,数据库使用mysql,使用B/S架构实现前台用户系统和后台管理员系统,和不同权限级别…...

web博客系统的自动化测试
目录 前言测试用例编写自动化脚本测试准备博客登录页相关测试用例登陆成功登录失败 博客首页相关测试用例登陆成功登录失败 博客详情页相关测试用例登录成功登录失败 博客编辑页相关测试用例登陆成功登录失败 编写测试文档测试类型内容 前言 本次测试是运用个人写的一个博客系…...

【论文阅读】Multi-level Semantic Feature Augmentation for One-shot Learning
用于单样本学习的多层语义特征增强 引用:Chen, Zitian, et al. “Multi-level semantic feature augmentation for one-shot learning.” IEEE Transactions on Image Processing 28.9 (2019): 4594-4605. 论文地址:下载地址 论文代码:https:…...

网络知识面试
1、http状态码 101: 切换请求协议 200:(请求成功)。服务器已成功处理了请求。 通常,这表示服务器提供了请求的网页。 301 : (永久移动,永久性重定向,会缓存) 请求的网页已永久移动到新位置。 服务器返回此响应(对 GET 或 HEAD 请求的响应)时,会自动将请求者转到新位置。…...

图片预览 图片上传到服务器
首先要明白 理解 multipart/form-data:multipart/form-data是一种在HTTP请求中使用的MIME类型,主要用于在客户端和服务器之间传输包含文件或二进制数据的表单数据。它通过一个边界(boundary)来分隔不同的表单字段和文件数据。…...

前端:base64的作用
背景 项目中发现,img标签中写src,读取一个png图片,只有16kb,速度特别慢。 解决办法,将图片转为base64,然后读取,速度特别快17ms就解决。 定义:base64是一种基于64个可打印字符(A-…...

Django在fitler过滤不等于的条件
提问 django 在API接口fitler的时候如何过滤 category 不等于6的 解答 为了在AoYuStudentFilter中设置过滤category不等于6的条件,需要使用django_filters库中的exclude方法。不过直接在FilterSet中使用exclude可能不那么直观,因为FilterSet主要设计用…...

Spring Boot英语知识分享网站:技术与实践
2相关技术 2.1 MYSQL数据库 MySQL是一个真正的多用户、多线程SQL数据库服务器。 是基于SQL的客户/服务器模式的关系数据库管理系统,它的有点有有功能强大、使用简单、管理方便、安全可靠性高、运行速度快、多线程、跨平台性、完全网络化、稳定性等,非常…...

京准电钟:NTP网络校时服务器从入门到精准
京准电钟:NTP网络校时服务器从入门到精准 京准电钟:NTP网络校时服务器从入门到精准 1.前言 由计算机网络系统组成的分布式系统,若想协调一致进行:IT行业的“整点开拍”、“秒杀”、“Leader选举”,通信行业的“同步…...

C++趣味编程玩转物联网:用树莓派Pico控制四位数码管
数码管是一种常用的数字显示器件,广泛应用于电子时钟、记分牌和智能设备显示界面。在本项目中,我们将通过树莓派Pico板控制一个四位数码管模块,展示从 0000 到 9999 的数字动态显示。这不仅是一次硬件和软件结合的实践,还可以帮助…...

DRM(数字权限管理技术)防截屏录屏----视频转hls流加密、web解密播放
提示:视频转hls流加密、web解密播放 需求:研究视频截屏时,播放器变黑,所以先研究的视频转hls流加密 文章目录 [TOC](文章目录) 前言一、工具ffmpeg、openssl二、后端nodeexpress三、web播放四、文档总结 前言 HLS流媒体协议&a…...
实验三 z变换及离散时间LTI系统的z域分析
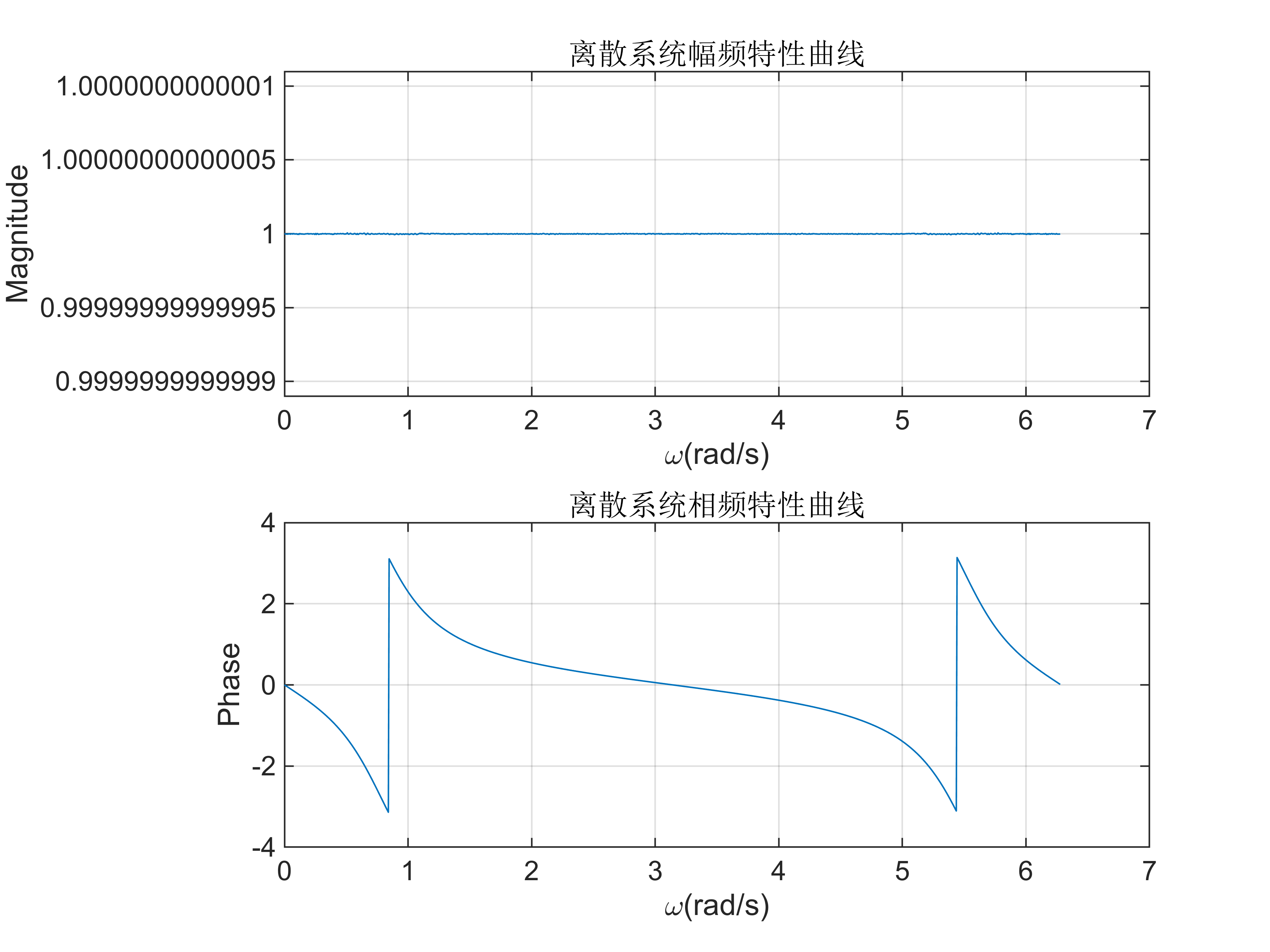
实验原理 有理函数z 变换的部分分式展开 【实例2-1】试用Matlab 命令对函数 X ( z ) 18 18 3 − 1 − 4 z − 2 − z − 3 X\left(z\right)\frac{18}{183^{-1} -4z^{-2} -z^{-3} } X(z)183−1−4z−2−z−318 进行部分分式展开,并求出其z 反变换。 B[18]; A…...

Python中的DrissionPage详解
文章目录 Python中的DrissionPage详解一、引言二、DrissionPage的基本使用1、安装与启动2、元素定位与操作 三、高级功能1、截图功能2、数据提取3、与其他库的集成 四、具体使用示例五、总结 Python中的DrissionPage详解 一、引言 DrissionPage是一个强大的Python库ÿ…...
python除了熟悉的pandas,openpyxl库也很方便的支持编辑Excel表
excel表格是大家经常用到的文件格式,各行各业都会跟它打交道。之前文章我们介绍了使用openpyxl和xlrd库读取excel表数据,使用xlwt库创建和编辑excel表,在办公自动化方面可以方便我们快速处理数据,帮助我们提升效率。 python之open…...

go语言怎么实现bash cmd里的mv功能?
在Go语言中实现类似于Bash命令行中的mv命令的功能,主要是通过文件系统的操作来完成的。mv命令可以用来移动文件或目录,也可以用来重命名文件或目录。在Go语言中,可以使用标准库中的os和io/ioutil包来实现这些功能。 以下是一个简单的例子&…...
)
Vue前端面试进阶(五)
使用Element UI开发的实际项目 在实际项目中,我使用Element UI来快速构建用户界面。Element UI是一套为开发者、设计师和产品经理准备的基于Vue 2.0的桌面端组件库,它提供了丰富的UI组件,极大地提高了开发效率。然而,在使用过程中…...

面试手撕题积累
1、实现滑动窗口限流,允许每分钟最多有100个请求 阿里一面题。 核心: 时间窗口管理:滑动窗口会根据时间流逝不断更新,需要记录请求的时间戳,并根据当前时间计算窗口内的请求数量。 限流判断:每次请求到来…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

CSS3相关知识点
CSS3相关知识点 CSS3私有前缀私有前缀私有前缀存在的意义常见浏览器的私有前缀 CSS3基本语法CSS3 新增长度单位CSS3 新增颜色设置方式CSS3 新增选择器CSS3 新增盒模型相关属性box-sizing 怪异盒模型resize调整盒子大小box-shadow 盒子阴影opacity 不透明度 CSS3 新增背景属性ba…...

负载均衡器》》LVS、Nginx、HAproxy 区别
虚拟主机 先4,后7...

DAY 45 超大力王爱学Python
来自超大力王的友情提示:在用tensordoard的时候一定一定要用绝对位置,例如:tensorboard --logdir"D:\代码\archive (1)\runs\cifar10_mlp_experiment_2" 不然读取不了数据 知识点回顾: tensorboard的发展历史和原理tens…...

2025-05-08-deepseek本地化部署
title: 2025-05-08-deepseek 本地化部署 tags: 深度学习 程序开发 2025-05-08-deepseek 本地化部署 参考博客 本地部署 DeepSeek:小白也能轻松搞定! 如何给本地部署的 DeepSeek 投喂数据,让他更懂你 [实验目的]:理解系统架构与原…...
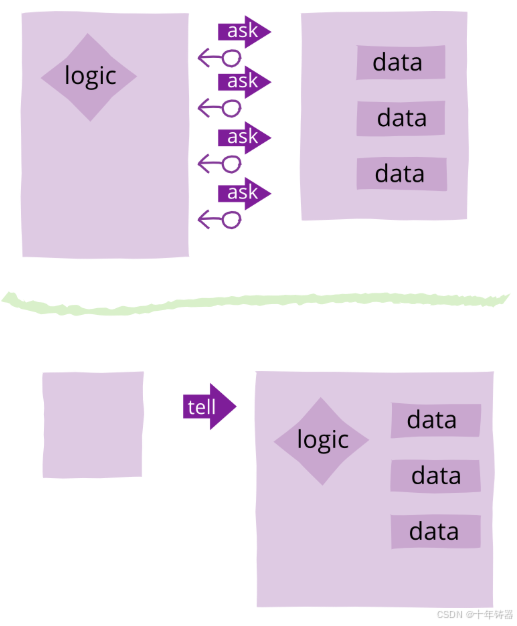
ABAP设计模式之---“Tell, Don’t Ask原则”
“Tell, Don’t Ask”是一种重要的面向对象编程设计原则,它强调的是对象之间如何有效地交流和协作。 1. 什么是 Tell, Don’t Ask 原则? 这个原则的核心思想是: “告诉一个对象该做什么,而不是询问一个对象的状态再对它作出决策。…...
