PID控制算法简介
目录
1 简介
2 比例Proportional
3 积分Integral
4 微分Differential
5 公式
6 积分限幅
7 积分限行
8 相关代码
1 简介
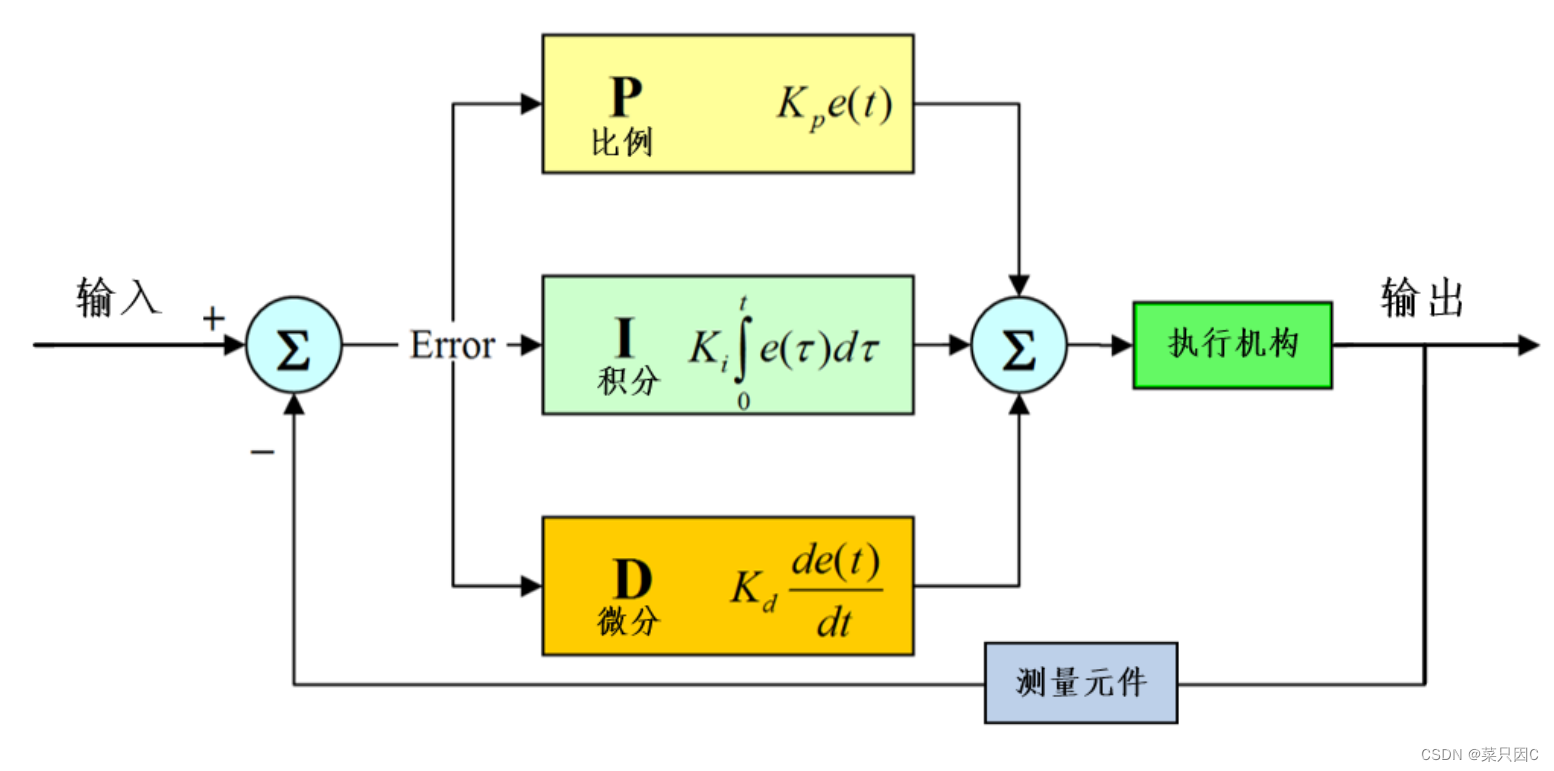
PID控制中有P、I、D三个参数,PID即:Proportional(比例)、Integral(积分)、Differential(微分)的缩写。只有明白这三个参数的含义和作用才能完成控制器PID参数整定,让控制器到达最佳控制效果。
PID是经典的闭环控制算法,具有原理简单,易于实现,适用面广,控制参数相互独立,参数的选定比较简单等优点。
凡是需要将某一个物理量“保持稳定”的场合(比如维持平衡,稳定温度、转速等),PID都会派上大用场。
2 比例Proportional
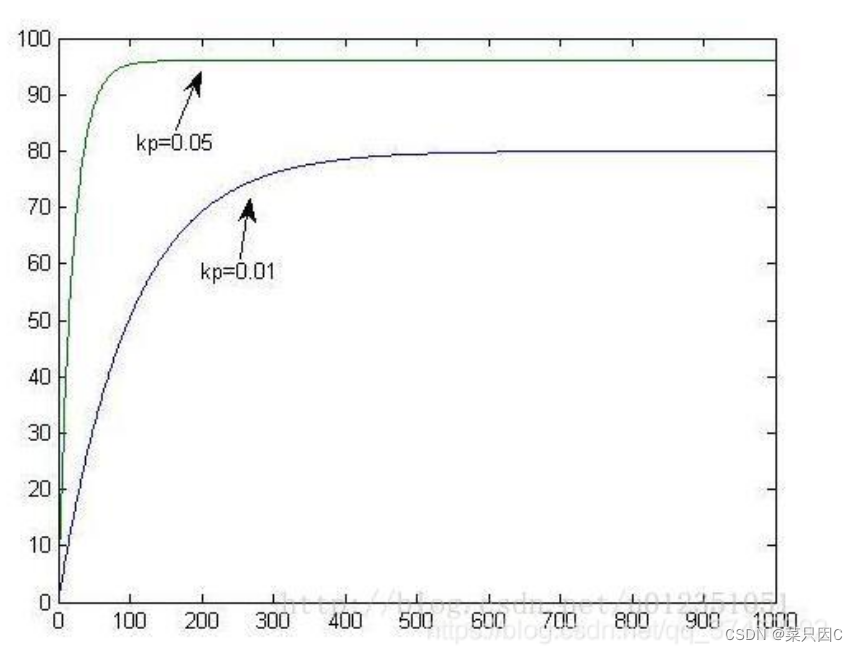
比例控制器实际上就是个放大倍数可调的放大器,即△P=Kp×e,式中Kp为比例增益,即Kp可大于1,也可小于1;e为控制器的输入,也就是测量值与给定值之差,又称为偏差。
比例控制有个缺点,就是会产生余差,要克服余差就必须引入积分作用。
只有比例系数无法准确到达目标位置,但增大比例系数有利于减小误差
3 积分Integral
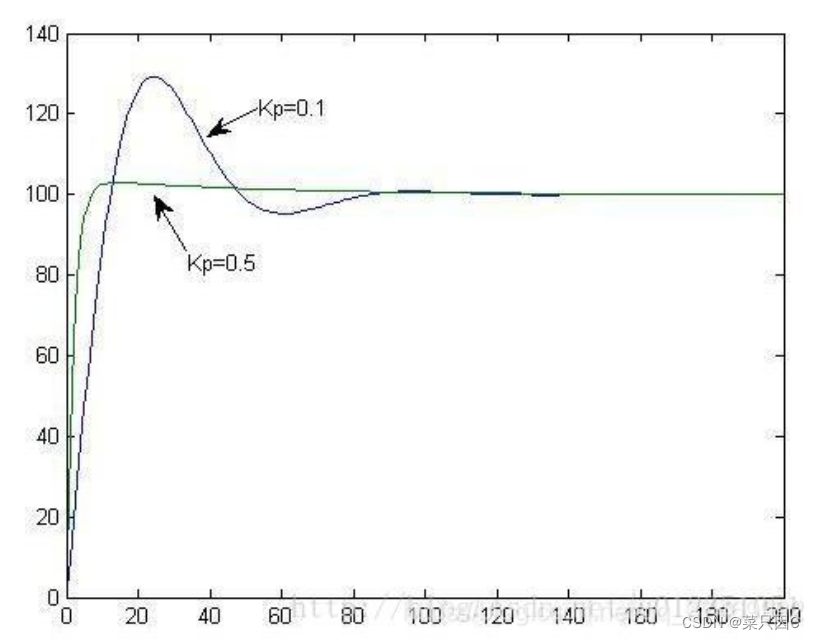
控制器的积分作用就是为了消除自控系统的余差而设置的。所谓积分,就是随时间进行累积的意思,即当有偏差输入e存在时,积分控制器就要将偏差随时间不断累积起来,也就是积分累积的快慢与偏差e的大小和积分速度成正比。只要有偏差e存在,积分控制器的输出就要改变,也就是说积分总是起作用的,只有偏差不存在时,积分才会停止。
实际上积分作用很少单独使用,通常与比例作用一起使用,使其既具有把偏差放大(或缩小)的比例作用,又具有将偏差随时间累积的积分作用,且其作用方向是一致的。这时控制器的输出为:△P=Ke+△Pi,式中△P为控制器输出值的变化;Ke为比例作用引起的输出;△Pi为积分作用引起的输出。
同时使用比例系数和积分可以准确到达目标位置,但当比例系数过大时会出现不稳定性
4 微分Differential
微分作用主要是用来克服被控对象的滞后,常用于温度控制系统。除采用微分作用外,在使用控制系统时要注意测量传送的滞后问题,如温度测量元件的选择和安装位置等。
在常规PID控制器中,微分作用的输出变化与微分时间和偏差变化的速度成比例,而与偏差的大小无关,偏差变化的速度越大,微分时间越长,则微分作用的输出变化越大。但如果微分作用过强,则可能由于变化太快而由其自身引起振荡,使控制器输出中产生明显的“尖峰”或“突跳”。为了避免这一扰动,在PID调节器和DCS中可使用微分先行PID运算规律,即只对测量值PV进行微分,当人工改变控制器的给定值SP时,不会造成控制器输出的突变,避免了改变SP的瞬间给控制系统带来的扰动。如TDC-3000,则在常规PID算法中增加一个软开关,组态时供用户选择控制器对偏差、还是测量值进行微分。
微分保证系统能够平稳运行,不至于出现太大的波动
5 公式
连续形式:
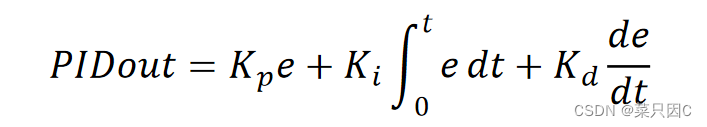
离散形式(常用,由连续形式推导):
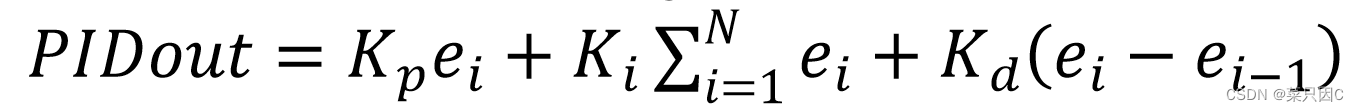
6 积分限幅
试想一下,使用P和I项进行控制,无人机在地面准备起飞,期望高度是100m。此时一个人摁住无人机,那么误差值一直为100m,控制器P项输出保持不变,控制器I项输出是线性增长的
一段时间后,那个人突然不摁了,此时控制器I项输出可能非常大,再加上控制器P项输出,控制器给电机的输出非常大,那么无人机速度就非常快并且飞的非常高。对于这种情况,我们对积分限幅,I项增加到一定值时就不再增了。那么无人机在上面这种情况下就不至于飞的很快很高,这就是积分限幅的作用。
7 积分限行
我们直接将传感器的反馈值分出来一路给到控制器的D项,这样做有一个好处就是如果希望无人机快速反应移动,当期望高度突变的时候,影响会先给到P和I项,由于开始时无人机位置没有突变,传感器反馈的实际高度值也不会突变,因此不会马上给到D项,这样就有效减小了D项开始的缓冲作用,使无人机可以快速反应移动。如果不这样做,那么如果期望高度突变,D项的微分值也会突变变得很大,缓冲作用非常大,使相应效果大大降低。
8 相关代码
chassis_motor_pid[i].SpeedPID.current=motor_chassis[i].speed_rpm;
pid_calc(&chassis_motor_pid[i].SpeedPID);void pid_calc(_pid* pid)
{pid->e=pid->target-pid->current;pid->p_out=(int32_t)(pid->Kp*pid->e);if(fabs(pid->e)<I_Band)//积分限幅和积分分离 {pid->i_out+=(int32_t)(pid->Ki*pid->e);limit(&(pid->i_out),pid->IntegralLimit);}else{pid->i_out=0;}pid->d_out=(int32_t)(pid->Kd*(pid->e-pid->last_e));pid->total_out=pid->p_out+pid->i_out+pid->d_out;//公式 limit(&(pid->total_out),pid->MaxOutput);//输出限制 pid->last_e=pid->e;//更新last值 } 相关文章:
PID控制算法简介
目录 1 简介 2 比例Proportional 3 积分Integral 4 微分Differential 5 公式 6 积分限幅 7 积分限行 8 相关代码 1 简介 PID控制中有P、I、D三个参数,PID即:Proportional(比例)、Integral(积分&#…...
【王道数据结构】第八章 | 排序
目录 8.1. 排序的基本概念 8.2. 插入排序 8.2.1. 直接插入排序 8.2.2. 折半插入排序 8.2.3. 希尔排序 8.3. 交换排序 8.3.1. 冒泡排序 8.3.2. 快速排序 8.4. 选择排序 8.4.1. 简单选择排序 8.4.2. 堆排序 8.5. 归并排序和基数排序 8.5.2. 基数排序 8.1. 排序的基本概念 排…...
95后外贸SOHO,年入7位数,他究竟是怎么做的?
外贸SOHO,一年到底能挣多少钱?有人说:“勤勤恳恳,年薪也就十来万吧”;也有人说:“100万而已我早就已经挣到了”;还有人说:“谁说新手难出头?我做跨境半年赚200万…...
2023年全国最新消防设施操作员精选真题及答案
百分百题库提供消防设施操作员考试试题、消防设施操作员考试预测题、消防设施操作员考试真题、消防设施操作员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 一、多选题 15、以下符合电气火灾监控系统监控设备的安装要求的有:( ) A、…...

mysql 无需修改配置文件,即可改变表数据存储位置
由于Linux系统的mysql 默认数据存储在/var/lib/mysql路径下,而该路径装系统时默认大小仅50G,当我们的数据稍微大一点时就会把该空间占满,无法再插入数据。 针对该问题有两种解决办法: 1、修改/etc/my.cnf配置文件,重启…...

轻松解决Session-Cookie 鉴权(含坑)附代码
Session-Cookie 鉴权 cookie介绍 Cookie 存储在客户端,可随意篡改,不安全有大小限制,最大为 4kb有数量限制,一般一个浏览器对于一个网站只能存不超过 20 个 Cookie,浏览器一般只允许存放 300个 CookieCookie 是不可跨…...

pyinstaller使用详细
目录常用命令spec文件配置报错常用命令 pyinstaller -D xxx.py //打包生成目录(director)pyinstaller -F xxx.py//打包生成单个exe文件pyinstaller xxx.spec //根据现有的spec文件进行打包运行以上命令之一后会生成build、dist文件夹以及xxx.spec文件&a…...
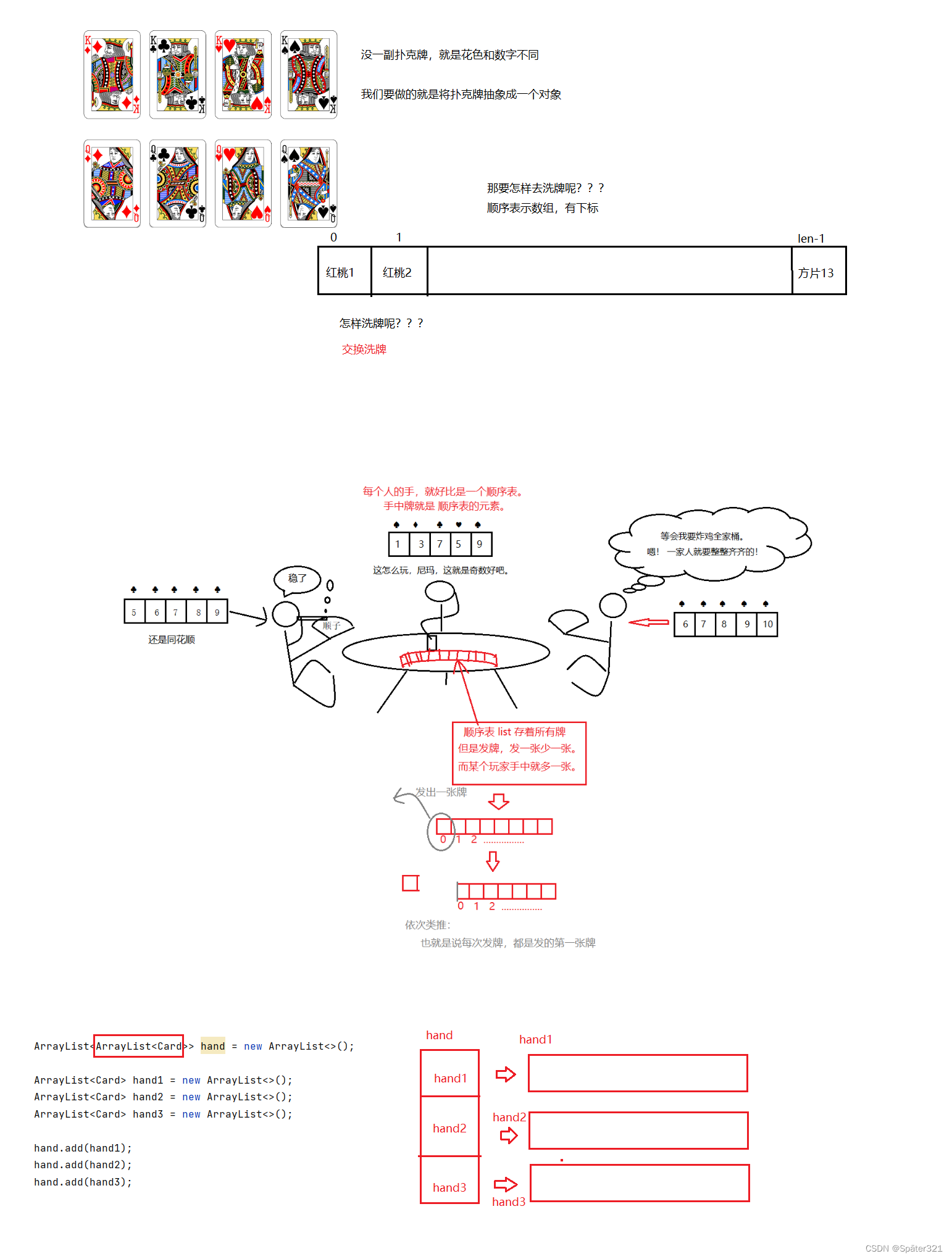
java -数据结构,List相关基础知识,ArrayList的基本使用,泛型的简单、包装类介绍
一、 预备知识-泛型(Generic) 1.1、泛型的引入 比如:我们实现一个简单的顺序表 class MyArrayList{public int[] elem;public int usedSize;public MyArrayList(){this.elem new int[10];}public void add(int key){this.elem[usedSize] key;usedSize;}public …...
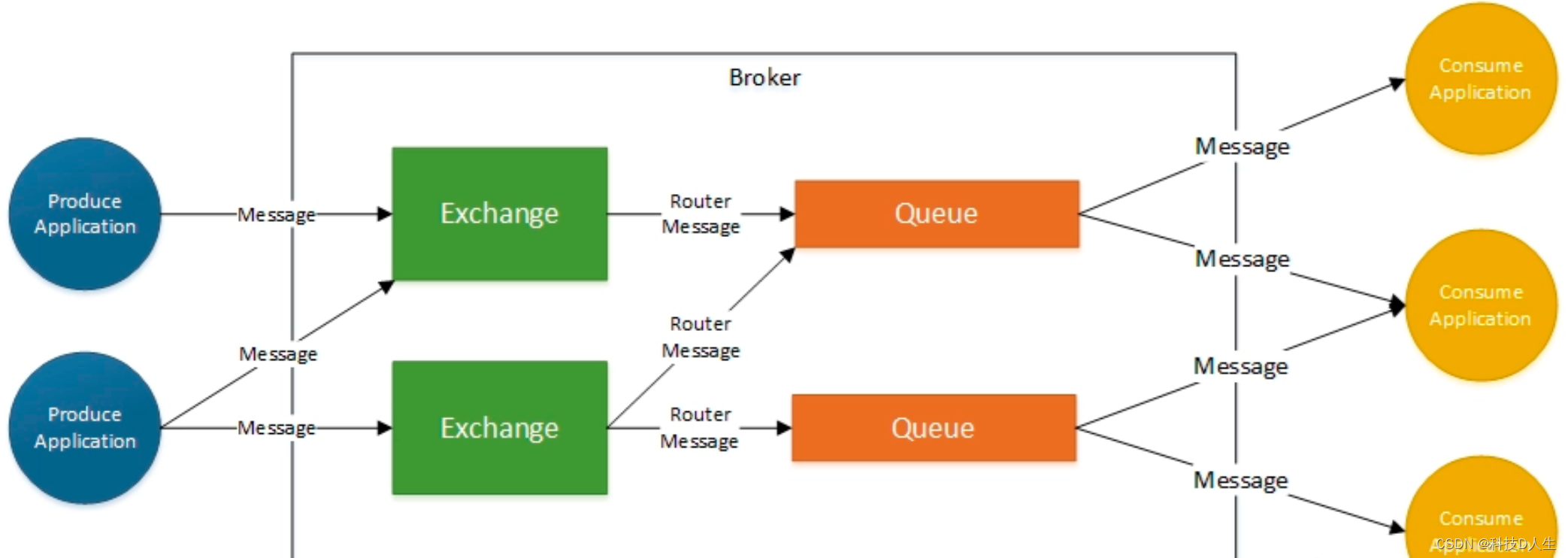
RabbitMQ学习总结(10)—— RabbitMQ如何保证消息的可靠性
一、丢失场景 RabbitMQ丢失的以下3种情况: (1)生产者:生产者发送消息至MQ的数据丢失...

购物车案例【版本为vue3】
前言: 首先我们要明白整个购物车的组成。它是由一个主页面加两个组件组合成的。本章主要运用父子之间的通讯: 父传子 子传父 首先新建一个vue3项目,这里有俩种创建方式: vue-cli : ● 输入安装指令 npm init vuelates…...

Multisim14 安装包及安装教程
Multisim14 安装教程 Multisim14下载地址:Kevin的学习站–安装包下载地址 Multisim14 简介: Multisim 14 是美国国家仪器有限公司(National Instrument,NI)推出的以 Windows 为基础、符合工业标准的、具有 SPICE 最佳仿…...

Java实现简单的图书管理系统源码+论文
简单图书管理系统设计(文末附带源码论文) 为图书管理人员编写一个图书管理系统,图书管理系统的设计主要是实现对图书的管理和相关操作,包括3个表: 图书信息表——存储图书的基本信息,包括书号、书名、作者…...
前端调试2
一、用chrome调试(node.js)例:const fs require(fs/promises);(async function() {const fileContent await fs.readFile(./package.json, {encoding: utf-8});await fs.writeFile(./package2.json, fileContent); })();1.先 node index.js 跑一下:2.然…...

AlphaFold 2 处理蛋白质折叠问题
蛋白质是一个较长的氨基酸序列,比如100个氨基酸的规模,如此长的氨基酸序列连在一起是不稳定的,它们会卷在一起,形成一个独特的3D结构,这个3D结构的形状决定了蛋白质的功能。 蛋白质结构预测(蛋白质折叠问题…...

问卷调查会遇到哪些问题?怎么解决?
提到问卷调查我们并不陌生,它经常被用作调查市场、观察某类群体的行为特征等多种调查中。通过问卷调查得出的数据能够非常真实反映出是市场的现状和变化趋势,所以大家经常使用这个方法进行调查研究。不过,很多人在进行问卷调查的时候也会遇到…...
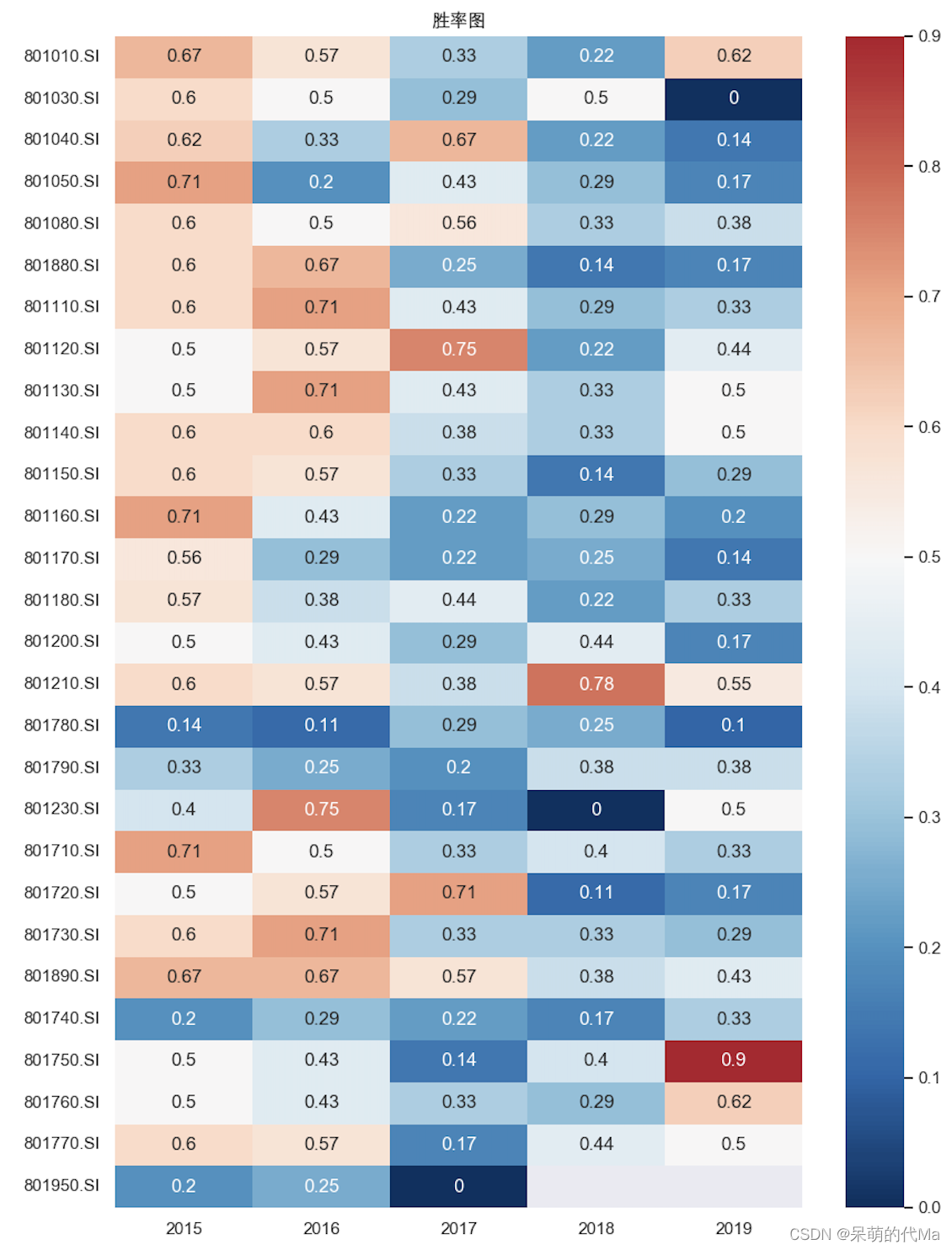
量化选股——基于动量因子的行业风格轮动策略(第1部分—因子测算)
文章目录动量因子与行业轮动概述动量因子的理解投资视角下的行业轮动现象投资者视角与奈特不确定性动量因子在行业风格上的效果测算动量因子效果测算流程概述1. 行业选择:申万一级行业2. 动量因子选择:阿隆指标(Aroon)3. 测算方法…...

工作常用git命令
修改hard:git reset --hard md5git push -f合并多次commitsgit rebase -i HEAD~4git push -f冲突文件被覆盖冲突文件被覆盖了,可以用git checkout commitId /path来快速把一个或一些文件还原会之前的提交,重新commit ,merge一次删除分支git b…...

test3
数据链路层故障分析 一、网桥故障 a.主要用途简述 网桥作为一种桥接器,可以连接两个局域网。工作在数据链路层,是早期的两端口二层网络设备。可将一个大的VLAN分割为多个网段,或者将两个以上的LAN互联为一个逻辑LAN,使得LAN上的…...

领证啦,立抵3600,软考证书到手后还有很多作用
2022年下半年软考合格证书发放在2023年2月-3月进行,目前已有多个省市开始发证了,比如上海、江苏、辽宁、浙江、山东等地。还没收到领证通知的考生也不要着急,可以关注当地软考办通知。 拿到证书的朋友可以去申请入户,职称评聘&am…...
响应式布局之viewport-超级简单
之前文章CSS布局之详解_故里2130的博客-CSDN博客 上面的文章可以实现响应式布局,根据浏览器的大小变化而变化,但是相对于viewport来说,之前的还是有点复杂,而使用viewport更加的简单。 当我们使用amfe-flexible的时候࿰…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...
