什么是默克尔树(Merkle Tree)?如何计算默克尔根?
默克尔树的概念
默克尔树(Merkle Tree)是一种特殊的二叉树,它的每个节点都存储了一个数据块的哈希值。哈希值是一种可以将任意长度的数据转换为固定长度的字符串的算法,它具有唯一性和不可逆性的特点,即不同的数据块会产生不同的哈希值,而相同的数据块会产生相同的哈希值,且无法从哈希值还原出原始数据。默克尔树的叶子节点存储了数据块本身的哈希值,而非叶子节点存储了其子节点哈希值的组合的哈希值。这样,默克尔树的根节点就包含了所有数据块的哈希信息,可以用来代表整棵树的唯一标识。
默克尔树的结构
默克尔树是一种完全二叉树,即每个非叶子节点都有两个子节点,如果数据块的数量不是2的整数次幂,那么就需要复制最后一个数据块来补齐。例如,如果有5个数据块,那么就需要复制第5个数据块来构成6个数据块,然后再复制第6个数据块来构成8个数据块。这样,就可以形成一个4层的完全二叉树.
如下图所示: 在这个例子中,A、B、C、D、E、F、G、H是8个数据块,它们经过哈希函数H得到8个哈希值H(A)、H(B)、H(C)、H(D)、H(E)、H(F)、H(G)、H(H),这些哈希值作为叶子节点。然后,叶子节点两两组合,得到4个中间节点H(H(A)+H(B))、H(H(C)+H(D))、H(H(E)+H(F))、H(H(G)+H(H)),其中+表示字符串连接。再然后,中间节点两两组合,得到2个中间节点H(H(H(A)+H(B))+H(H(C)+H(D)))和H(H(H(E)+H(F))+H(H(G)+H(H)))。最后,这两个中间节点组合得到根节点H(H(H(H(A)+H(B))+H(H(C)+H(D)))+H(H(H(E)+H(F))+H(H(G)+H(H))))。这个根节点就是默克尔根(Merkle Root),它包含了所有数据块的哈希信息。
暂时无法在飞书文档外展示此内容
默克尔树的作用
默克尔树有以下几个作用: 1.数据完整性验证:通过比较两棵默克尔树的根节点是否相同,可以快速判断两份数据是否完全一致。如果根节点不同,则说明至少有一个数据块发生了变化;如果根节点相同,则说明所有数据块都没有变化。这样可以节省大量的比较时间和空间。 2.数据安全性保护:由于哈希函数的不可逆性,即使知道了默克尔根和部分数据块,也无法还原出其他数据块的内容。这样可以保护数据的隐私和安全。 3.数据有效性证明:通过提供某个数据块及其对应的默克尔路径(Merkle Path),即从该数据块到根节点经过的所有节点的哈希值,可以证明该数据块确实存在于某棵默克尔树中。这样可以避免传输整棵默克尔树,只需要传输默克尔根和默克尔路径即可。
默克尔树的应用
默克尔树广泛应用于文件系统和P2P网络中,例如:
1.Git:Git是一种分布式版本控制系统,它使用默克尔树来存储和管理文件的历史版本。每个文件都有一个哈希值,每个目录也有一个哈希值,这些哈希值构成了一棵默克尔树。每次提交(commit)都会生成一个新的默克尔根,作为该提交的唯一标识。这样,可以快速比较不同提交之间的差异,以及验证文件的完整性和有效性。
2.BitTorrent:BitTorrent是一种P2P文件共享协议,它使用默克尔树来分割和校验大文件。每个文件被切分成多个数据块,每个数据块有一个哈希值,这些哈希值构成了一棵默克尔树。每个文件的元数据(metadata)中包含了该文件的默克尔根和数据块的大小。这样,可以在下载过程中验证数据块的完整性和有效性,以及恢复损坏的数据块。
3.Bitcoin:Bitcoin是一种去中心化的数字货币系统,它使用默克尔树来存储和验证交易记录。每个交易都有一个哈希值,这些哈希值构成了一棵默克尔树。每个区块(block)中包含了该区块的默克尔根和交易数量。这样,可以在不传输整个区块的情况下,证明某个交易是否存在于某个区块中,以及验证区块的完整性和有效性。 默克尔树是一种特殊的二叉树,它的每个节点都存储了一个数据块的哈希值。
相关文章:
?如何计算默克尔根?)
什么是默克尔树(Merkle Tree)?如何计算默克尔根?
默克尔树的概念 默克尔树(Merkle Tree)是一种特殊的二叉树,它的每个节点都存储了一个数据块的哈希值。哈希值是一种可以将任意长度的数据转换为固定长度的字符串的算法,它具有唯一性和不可逆性的特点,即不同的数据块会产生不同的哈希值&…...

眼部按摩仪WT2605音频蓝牙语音芯片方案 单芯片实现语音提示及控制/手机无线音频传输功能
随着科技的快速发展,人们的生活方式也在不断改变,智能化、便捷化的产品逐渐成为市场的主流。眼部按摩仪作为一种结合了现代科技与健康生活理念的产品,受到了广大消费者的青睐。而在众多眼部按摩仪中,采用WT2605音频蓝牙芯片的方案…...

python打包深度学习虚拟环境
今天师兄让我把环境打包发给他,我才知道可以直接打包深度学习虚拟环境,这样另一个人就不用辛辛苦苦的去装环境了,我们都知道有些论文他需要的环境很难装上。比如装Apex,装 DCN,mmcv-full 我现在把3090机子上的ppft虚拟…...

springboot358智慧社区居家养老健康管理系统(论文+源码)_kaic
毕 业 设 计(论 文) 智慧社区居家养老健康管理系统设计与实现 摘 要 传统办法管理信息首先需要花费的时间比较多,其次数据出错率比较高,而且对错误的数据进行更改也比较困难,最后,检索数据费事费力。因此&…...
复杂网络(二)
一、网络的基本静态几何特征 1.1 度分布 节点的度:在网络中,节点的邻边数称为该节点的度 对于网络中所有节点的度求平均,可得到网络的平均度 度分布:大多数实际网络中的节点的度满足一定的概率分布。定义P(k)为网络中度为k的节…...

Kubernetes 01
MESOS:APACHE 分布式资源管理框架 2019-5 Twitter退出,转向使用Kubernetes Docker Swarm 与Docker绑定,只对Docker的资源管理框架,阿里云默认Kubernetes Kubernetes:Google 10年的容器化基础框架,borg…...

node修改文件名称
node修改名称 var fs require(fs); const events require(events); var path require(path);init(); function init() {//要遍历的文件夹所在的路径const dirPath path.resolve(__dirname, "data");//遍历目录fileDisplay(dirPath); }/*** 文件遍历* param dirP…...
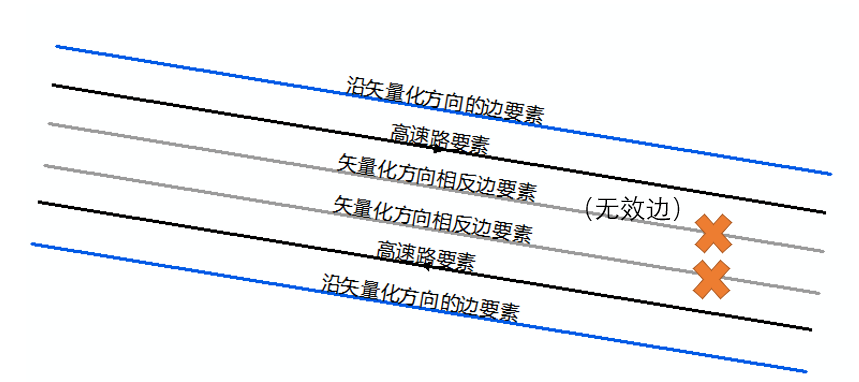
ArcGIS 软件中路网数据的制作
内容导读 路网数据是进行网络分析的基础,它是建立网络数据集的数据来源。 本文我们以OSM路网数据为例,详细介绍OSM路网数据从下载,到数据处理,添加属性,完成符合网络分析的网络数据集的全部过程。 01 数据获取 比较…...

transformers microsoft--table-transformer 表格识别
一、安装包 pip install transformers pip install torch pip install SentencePiecepip install timm pip install accelerate pip install pytesseract pillow pandas pip install tesseract 下载模型: https://huggingface.co/microsoft/table-transformer-s…...

【Spark源码分析】规则框架-草稿
规则批:规则集合序列,由名称、执行策略、规则列表组成。一个规则批里使用一个执行规则。 执行策略 FixedPointOnce 规则: #mermaid-svg-1cvqR4xkYpMuAs77 {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px…...

迪米特原则的理解和实践
迪米特原则(Law of Demeter,简称LoD),也被称为最少知识原则(Least Knowledge Principle,LKP),是面向对象设计中的一个重要原则。其核心思想是:一个对象应该对其他对象有最…...
)
jQuery零基础入门速通(中)
大家好,我是小黄。 在上一篇文章中,我们初步了解了jQuery的基本概念、环境搭建、选择器、基本的DOM操作以及事件处理。接下来,我们将继续深入探讨jQuery的DOM操作和事件处理,以及一些实用的技巧和高级用法。 五、高级DOM操作 5…...

【设计模式系列】中介者模式(十八)
一、什么是中介者模式 中介者模式(Mediator Pattern)是一种行为型设计模式,其核心思想是通过一个中介者对象来封装一系列对象之间的交互,使这些对象不需要相互显式引用。中介者模式提供了一个中介层,用以协调各个对象…...

PDF版地形图矢量出现的问题
项目描述:已建风电场道路测绘项目,收集到的数据为PDF版本的地形图,图上标注了项目竣工时期的现状,之后项目对施工区域进行了复垦恢复地貌,现阶段需要准确的知道实际复垦修复之后的道路及其它临时用地的面积 解决方法&…...

小迪安全第四十二天笔记 简单的mysql注入 mysql的基础知识 用户管理数据库模式 mysql 写入与读取 跨库查询
前言 之前的安全开发我们学习了 php联动数据库的模式 ,这个模式是现在常用的模式 这一节来学习 如何 进行数据库的注入和数据库相关知识 1、了解数据库的结构 我们使用 navicate连接数据库之后看一下 一共四层结构 库 》表》字段》数据 这个层级关系…...

11.25.2024刷华为OD
文章目录 HJ76 尼科彻斯定理(观察题,不难)HJ77 火车进站(DFS)HJ91 走格子方法,(动态规划,递归,有代表性)HJ93 数组分组(递归)语法知识…...
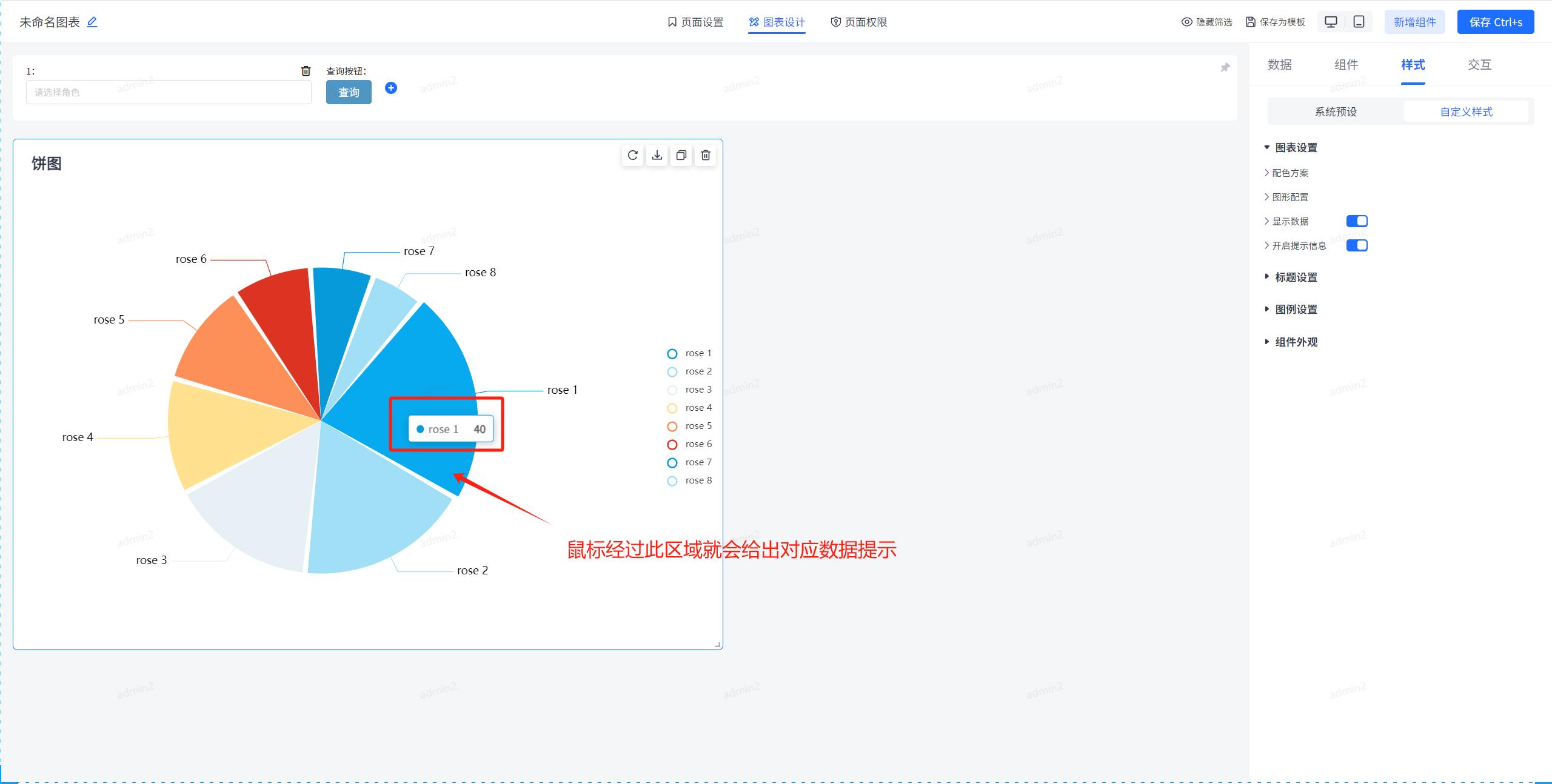
你真的会用饼图吗?JVS-智能BI饼图组件深度解析
在数据可视化的世界里,饼图是我们常见的一种可视化图形。在JVS-智能BI中提供了数据可视化饼图组件,接下来我通过这篇文章详细介绍,从配色方案到图形配置,从显示数据到提示信息,饼图的每一个细节配置。 饼图类图表概述…...

HarmonyOS Next 模拟器安装与探索
HarmonyOS 5 也发布了有一段时间了,不知道大家实际使用的时候有没有发现一些惊喜。当然随着HarmonyOS 5的更新也带来了很多新特性,尤其是 HarmonyOS Next 模拟器。今天,我们就来探索一下这个模拟器,看看它能给我们的开发过程带来什…...

医学机器学习:数据预处理、超参数调优与模型比较的实用分析
摘要 本文介绍了医学中的机器学习,重点阐述了数据预处理、超参数调优和模型比较的技术。在数据预处理方面,包括数据收集与整理、处理缺失值、特征工程等内容,以确保数据质量和可用性。超参数调优对模型性能至关重要,介绍了多种调…...

单片机知识总结(完整)
1、单片机概述 1.1. 单片机的定义与分类 定义: 单片机(Microcontroller Unit,简称MCU)是一种将微处理器、存储器(包括程序存储器和数据存储器)、输入/输出接口和其他必要的功能模块集成在单个芯片上的微型…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...
Android屏幕刷新率与FPS(Frames Per Second) 120hz
Android屏幕刷新率与FPS(Frames Per Second) 120hz 屏幕刷新率是屏幕每秒钟刷新显示内容的次数,单位是赫兹(Hz)。 60Hz 屏幕:每秒刷新 60 次,每次刷新间隔约 16.67ms 90Hz 屏幕:每秒刷新 90 次,…...

【阅读笔记】MemOS: 大语言模型内存增强生成操作系统
核心速览 研究背景 研究问题:这篇文章要解决的问题是当前大型语言模型(LLMs)在处理内存方面的局限性。LLMs虽然在语言感知和生成方面表现出色,但缺乏统一的、结构化的内存架构。现有的方法如检索增强生成(RA…...

简约商务通用宣传年终总结12套PPT模版分享
IOS风格企业宣传PPT模版,年终工作总结PPT模版,简约精致扁平化商务通用动画PPT模版,素雅商务PPT模版 简约商务通用宣传年终总结12套PPT模版分享:商务通用年终总结类PPT模版https://pan.quark.cn/s/ece1e252d7df...

Ray框架:分布式AI训练与调参实践
Ray框架:分布式AI训练与调参实践 系统化学习人工智能网站(收藏):https://www.captainbed.cn/flu 文章目录 Ray框架:分布式AI训练与调参实践摘要引言框架架构解析1. 核心组件设计2. 关键技术实现2.1 动态资源调度2.2 …...
