复杂网络(二)
一、网络的基本静态几何特征
1.1 度分布
节点的度:在网络中,节点的邻边数
称为该节点的度
对于网络中所有节点的度求平均,可得到网络的平均度
度分布:大多数实际网络中的节点的度满足一定的概率分布。定义P(k)为网络中度为k的节点在整个网络中所占的比例。
规则网络:由于每个节点具有相同的度,所以其度分布集中在一个单一尖峰上。是一种Deta分布。
完全随机网络:度分布具有Poisson分布的形式,每一条边的出现概率是相等的,大多数节点的度基本相同,并接近于网络平均度<k>,远离峰值<k>,度分布则按指数形式集聚下降。把这类网络称为均匀网络。
无标度网络:具有幂指数形式的度分布。所谓无标度是指一个概率分布函数F(x)对于任意给定常数a存在常数b使得F(x)满足F(ax) = bF(x)。
1.2 网络的直径和平均距离
网络中的两节点和
之间经历边数最少得一条简单路径(经历的边各不相同),称为测地线
测地线的边数称为两节点
和
之间的距离
网络的直径D定义为所有距离中的最大值
平均距离(特征路径长度)L定义为所有节点对之间距离的平均值,它描述了网络中节点间的平均分离程度,即网络有多小,计算公式为
很多实际网络虽然节点数巨大,但平均距离却小得惊人,这就是小世界效应
集聚系数:用以捕获给定节点的邻居节点之间的连接程度
1.3 度-度相关性
基于最近邻平均度值的度-度相关性
度-度相关性描述了网络中度大的节点和度小得节点之间的关系。若度大的节点倾向于和度大的节点连接,则网络是度-度正相关的;反之,若度大的节点倾向于和度小的节点连接,则网络是du-度负相关的。
节点的最近邻平均度值定义为
。
其中,表示节点
的度值,
为邻接矩阵元素。

基于Pearson相关系数的度-度相关性

1.4 介数和核度
介数:
介数分为节点介数和边介数两种,反映了节点或边在整个网络中的作用和影响力。
节点的介数定义为
式中,表示节点
和
之间的最短路径条数,
表示节点
和
之间的最短路径经过节点
的条数。
边的介数定义为
式中,表示节点
和
之间的最短路径系数条数,
表示节点
与
之间的最短路径经过边
的条数。
核度:
一个图的k-核是指反复去掉度值小于k的节点及其连线后,所剩余的子图,该子图的节点数就是该核的大小。若一个节点属于k-核,而不属于(k + 1)-核,则此节点的核度为k。节点核度的最大值叫做网络的核度。
网络密度:
网络密度指的是一个网络中各节点之间联络的紧密程度。网络G的网络密度d(G)定义为
,式中,M为网络中实际拥有的连接数,N为网络节点数。
二、代码实践
#Poisson分布(以ER网络为例)
# import networkx as nx
# import matplotlib.pyplot as plt
#
# #创建一个ER随机网络
n = 10000
# p = 0.001
# ER = nx.erdos_renyi_graph(n, p)
#
# #获取平均度
# d = dict(nx.degree(ER))
# print("平均度:", sum(d.values())/len(ER.nodes))
#
# #获取所有可能得度值对应的概率
# x = list(range(max(d.values())+1))
# y = [i/n for i in nx.degree_histogram(ER)]
# print("所有可能得度值对应的概率:", list(zip(x, y)))
# #绘制度分布图
# plt.plot(x, y)
# plt.xlabel("k")
# plt.ylabel("P(k)")
# plt.show()#幂律分布(以BA无标度网络为例)
import networkx as nx
import matplotlib.pyplot as plt
m = 3
BA = nx.barabasi_albert_graph(n, m)
#获取平均度
d = dict(nx.degree(BA))
print("平均度:", sum(d.values())/len(BA.nodes))
#获取所有可能得度值对应的概率
x = list(range(max(d.values())+1))
y = [i/n for i in nx.degree_histogram(BA)]
print("所有可能得度值对应的概率:", list(zip(x, y)))
#绘制度分布图
plt.plot(x, y)
plt.xlabel("k")
plt.ylabel("P(k)")
plt.show()#在双对数坐标轴下显示
plt.plot(x,y)
plt.xscale("log")
plt.yscale("log")
plt.xlabel("k")
plt.ylabel("P(k)")
plt.show()
#在双对数坐标轴下要把横坐标和纵坐标的0值排除
new_x = []
new_y = []
for i in range(len(x)):if y[i] != 0:new_x.append(x[i])new_y.append(y[i])
plt.plot(new_x,new_y)
plt.xscale("log")
plt.yscale("log")
plt.xlabel("k")
plt.ylabel("P(k)")
plt.show()相关文章:
复杂网络(二)
一、网络的基本静态几何特征 1.1 度分布 节点的度:在网络中,节点的邻边数称为该节点的度 对于网络中所有节点的度求平均,可得到网络的平均度 度分布:大多数实际网络中的节点的度满足一定的概率分布。定义P(k)为网络中度为k的节…...

Kubernetes 01
MESOS:APACHE 分布式资源管理框架 2019-5 Twitter退出,转向使用Kubernetes Docker Swarm 与Docker绑定,只对Docker的资源管理框架,阿里云默认Kubernetes Kubernetes:Google 10年的容器化基础框架,borg…...

node修改文件名称
node修改名称 var fs require(fs); const events require(events); var path require(path);init(); function init() {//要遍历的文件夹所在的路径const dirPath path.resolve(__dirname, "data");//遍历目录fileDisplay(dirPath); }/*** 文件遍历* param dirP…...
ArcGIS 软件中路网数据的制作
内容导读 路网数据是进行网络分析的基础,它是建立网络数据集的数据来源。 本文我们以OSM路网数据为例,详细介绍OSM路网数据从下载,到数据处理,添加属性,完成符合网络分析的网络数据集的全部过程。 01 数据获取 比较…...

transformers microsoft--table-transformer 表格识别
一、安装包 pip install transformers pip install torch pip install SentencePiecepip install timm pip install accelerate pip install pytesseract pillow pandas pip install tesseract 下载模型: https://huggingface.co/microsoft/table-transformer-s…...

【Spark源码分析】规则框架-草稿
规则批:规则集合序列,由名称、执行策略、规则列表组成。一个规则批里使用一个执行规则。 执行策略 FixedPointOnce 规则: #mermaid-svg-1cvqR4xkYpMuAs77 {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px…...

迪米特原则的理解和实践
迪米特原则(Law of Demeter,简称LoD),也被称为最少知识原则(Least Knowledge Principle,LKP),是面向对象设计中的一个重要原则。其核心思想是:一个对象应该对其他对象有最…...
)
jQuery零基础入门速通(中)
大家好,我是小黄。 在上一篇文章中,我们初步了解了jQuery的基本概念、环境搭建、选择器、基本的DOM操作以及事件处理。接下来,我们将继续深入探讨jQuery的DOM操作和事件处理,以及一些实用的技巧和高级用法。 五、高级DOM操作 5…...

【设计模式系列】中介者模式(十八)
一、什么是中介者模式 中介者模式(Mediator Pattern)是一种行为型设计模式,其核心思想是通过一个中介者对象来封装一系列对象之间的交互,使这些对象不需要相互显式引用。中介者模式提供了一个中介层,用以协调各个对象…...

PDF版地形图矢量出现的问题
项目描述:已建风电场道路测绘项目,收集到的数据为PDF版本的地形图,图上标注了项目竣工时期的现状,之后项目对施工区域进行了复垦恢复地貌,现阶段需要准确的知道实际复垦修复之后的道路及其它临时用地的面积 解决方法&…...

小迪安全第四十二天笔记 简单的mysql注入 mysql的基础知识 用户管理数据库模式 mysql 写入与读取 跨库查询
前言 之前的安全开发我们学习了 php联动数据库的模式 ,这个模式是现在常用的模式 这一节来学习 如何 进行数据库的注入和数据库相关知识 1、了解数据库的结构 我们使用 navicate连接数据库之后看一下 一共四层结构 库 》表》字段》数据 这个层级关系…...

11.25.2024刷华为OD
文章目录 HJ76 尼科彻斯定理(观察题,不难)HJ77 火车进站(DFS)HJ91 走格子方法,(动态规划,递归,有代表性)HJ93 数组分组(递归)语法知识…...
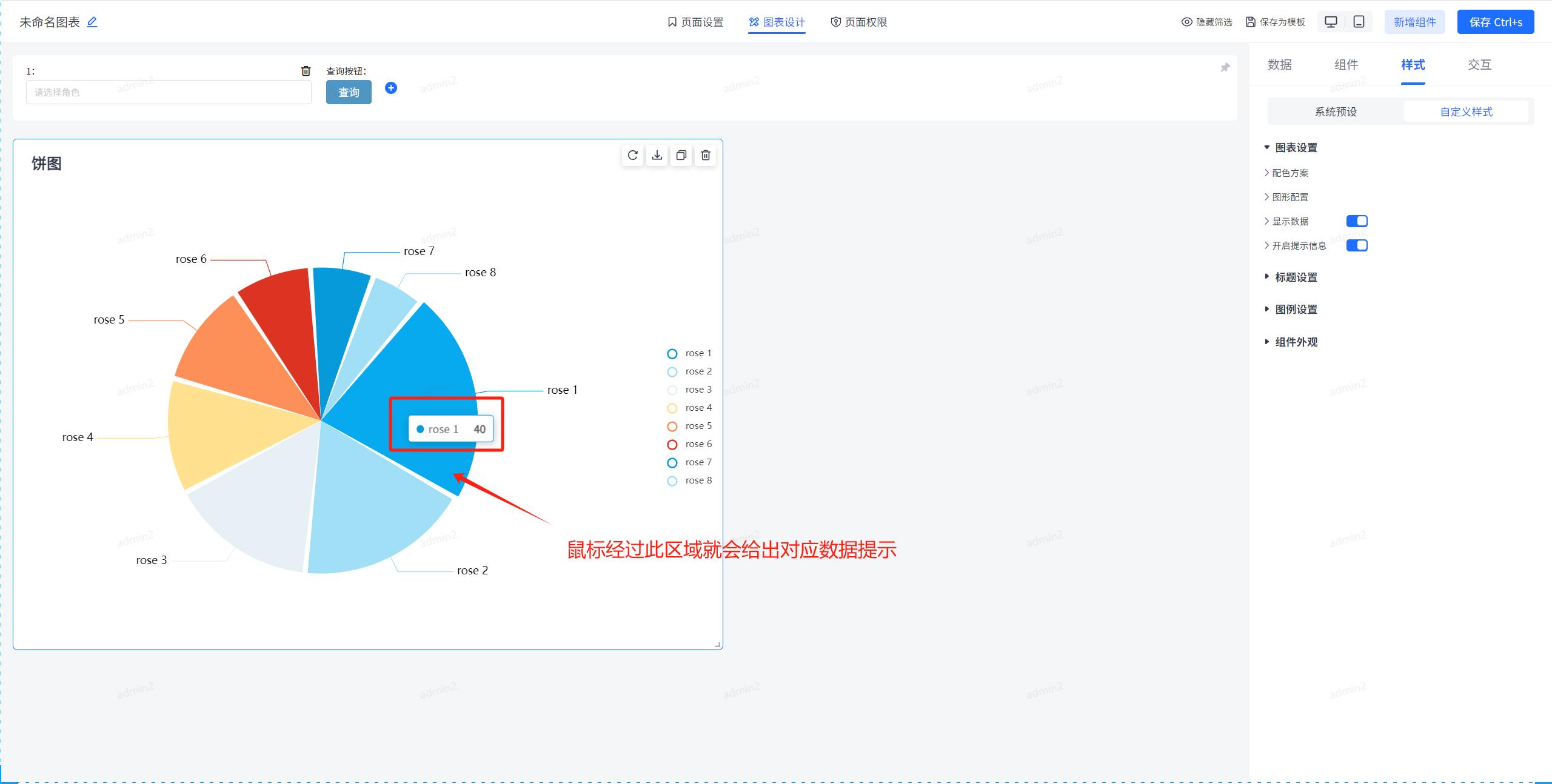
你真的会用饼图吗?JVS-智能BI饼图组件深度解析
在数据可视化的世界里,饼图是我们常见的一种可视化图形。在JVS-智能BI中提供了数据可视化饼图组件,接下来我通过这篇文章详细介绍,从配色方案到图形配置,从显示数据到提示信息,饼图的每一个细节配置。 饼图类图表概述…...

HarmonyOS Next 模拟器安装与探索
HarmonyOS 5 也发布了有一段时间了,不知道大家实际使用的时候有没有发现一些惊喜。当然随着HarmonyOS 5的更新也带来了很多新特性,尤其是 HarmonyOS Next 模拟器。今天,我们就来探索一下这个模拟器,看看它能给我们的开发过程带来什…...

医学机器学习:数据预处理、超参数调优与模型比较的实用分析
摘要 本文介绍了医学中的机器学习,重点阐述了数据预处理、超参数调优和模型比较的技术。在数据预处理方面,包括数据收集与整理、处理缺失值、特征工程等内容,以确保数据质量和可用性。超参数调优对模型性能至关重要,介绍了多种调…...

单片机知识总结(完整)
1、单片机概述 1.1. 单片机的定义与分类 定义: 单片机(Microcontroller Unit,简称MCU)是一种将微处理器、存储器(包括程序存储器和数据存储器)、输入/输出接口和其他必要的功能模块集成在单个芯片上的微型…...

【C++】auto和decltype类型推导关键字
1.C11关键字 auto和decltype是C11引入的关键字,负责类型的推导。所有不同的是: auto可直接用来定义变量,编译器会自动推导出变量的类型。decltype是推导出一个操作数的类型,然后用这个类型再去定义。 2.两者区别 尽管两者都是宏…...

OGRE 3D----3. OGRE绘制自定义模型
在使用OGRE进行开发时,绘制自定义模型是一个常见的需求。本文将介绍如何使用OGRE的ManualObject类来创建和绘制自定义模型。通过ManualObject,开发者可以直接定义顶点、法线、纹理坐标等,从而灵活地构建各种复杂的几何体。 Ogre::ManualObject 是 Ogre3D 引擎中的一个类,用…...

ARM + Linux 开发指南
随想:想写一个系列来讲如何嵌入式开发,然后能形成一个知识体系,帮助那些刚刚做嵌入开发的同学们. 1. ARM Linux从开机到Linux完全启动的流程和代码分析 ARM Linux从开机到完全启动的流程与代码分析 ARM Linux的启动过程主要涉及从设备上电开始,到Linux内核完全启动并进入…...

facebook欧洲户开户条件有哪些又有何优势?
在当今数字营销时代,Facebook广告已成为企业推广产品和服务的重要渠道。而为了更好地利用这一平台,广告主们需要理解不同类型的Facebook广告账户。Facebook广告账户根据其属性可分为多种类型,包括个人广告账户、企业管理(BM&#…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...

AD学习(3)
1 PCB封装元素组成及简单的PCB封装创建 封装的组成部分: (1)PCB焊盘:表层的铜 ,top层的铜 (2)管脚序号:用来关联原理图中的管脚的序号,原理图的序号需要和PCB封装一一…...
