蒙特卡洛方法(Monte Carlo,MC)
目录
1 序言
2 Monte Carlo法计算积分
3 最优化计算Monte Carlo法
1 序言
蒙特卡罗方法(Monte Carlo)是由冯诺依曼和乌拉姆等人发明的,“蒙特卡罗”这个名字是出自摩纳哥的蒙特卡罗赌场,这个方法是一类基于概率的方法的统称。是一种应用随机数来进行计算机模拟的方法,此方法随研究的系统进行随机观察抽样,通过对样本值的观察统计,求得所研究系统的某些参数。
2 Monte Carlo法计算积分
考虑二重积分
根据其几何意义,它是以f(x,y)为曲面顶,A为底的柱体C的体积。用下列简单思路求的近似值:假设C被包在几何体D的内部,D的体积已知,若在D内产生1个均分布的随机数,那么
P(随机数落在C内)C的体积/D的体积
现用Monte Carlo法计算:
% Monte Carlo Integration for f(x, y) = sqrt(1 - x^2) over x^2 + y^2 <= 1
clc; clear;% Number of random points
N = 1e6; % You can increase this for better accuracy% Initialize sum of function values
f_sum = 0;% Loop to generate random points and calculate contributions
for i = 1:N% Generate random (x, y) within the bounding box [-1, 1] x [-1, 1]x = -1 + 2*rand(); % Random x in [-1, 1]y = -1 + 2*rand(); % Random y in [-1, 1]% Check if the point is inside the circleif x^2 + y^2 <= 1f_sum = f_sum + sqrt(1 - x^2); % Accumulate the function valueend
end% Calculate area of the bounding box
A_box = 4; % The bounding box [-1, 1] x [-1, 1]% Calculate the integral estimate
integral_value = A_box * f_sum / N;% Display result
fprintf('Estimated value of the integral: %.6f\n', integral_value);2.1 代码解释:
1)随机点生成:
- 在 [−1,1]×[−1,1] 内均匀生成随机点。
- 使用条件
筛选落在单位圆内的点。
2)函数值累加:
- 对满足条件的点,计算
并累加到
f_sum。
3)积分估计公式:
- 估计积分值为:

- 这里的区域面积 Abox=4 是整个采样的矩形面积。
4)效率:
- N越大,估计值越准确。
- 通过筛选
,只在实际目标区域内计算函数值。
2.2 运算结果
| N = 1e2 | 2.655043 |
| N = 1e4 | 2.685272 |
| N = 1e6 | 2.666568 |
| N = 1e8 | 2.666756 |
3 最优化计算Monte Carlo法
求下列函数的最大值:
为了方便理解,先绘制这个函数:
% Define the function f(x)
f = @(x) (1 - x.^3) .* sin(3 * x);% Define the range for x
x = linspace(-2*pi, 2*pi, 1000); % Generate 1000 points in the range [-2*pi, 2*pi]% Compute the function values
y = f(x);% Plot the function
figure;
plot(x, y, 'b-', 'LineWidth', 1.5);
grid on;% Add labels and title
xlabel('x');
ylabel('f(x)');
title('Plot of f(x) = (1 - x^3)sin(3x)');
legend('f(x) = (1 - x^3)sin(3x)', 'Location', 'Best');
matlab运行结果如下:
在给出计算代码:
% Optimization using Monte Carlo for f(x) = (1 - x^3) * sin(3x)
clc; clear;% Number of random samples
N = 1e6; % Increase this for higher accuracy% Define the function
f = @(x) (1 - x.^3) .* sin(3 * x);% Generate random samples in the range [-2*pi, 2*pi]
x_samples = -2*pi + (2*pi - (-2*pi)) * rand(N, 1);% Evaluate the function for each sample
f_values = f(x_samples);% Find the maximum function value
f_max = max(f_values);% Find the corresponding x value(s) for the maximum
x_max = x_samples(f_values == f_max);% Display results
fprintf('Maximum value of f(x): %.6f\n', f_max);
fprintf('At x = %.6f (one of the possible values)\n', x_max(1));
3.1 代码解释
1)随机采样:
- 使用rand(N,1)生成N个均匀分布的随机数映射到区间[-2pi,2pi]中,作为函数的自变量x值。
2)函数评估:
- 定义函数
,计算每个采样点上的函数值
。
3)最大值搜索:
- 使用max函数找到函数值中的最大值
- 找到与最大值对应的x值。
4)输出结果:
- 输出最大值及对应的一个可能的必值(可能有多个全局最大值点)
2.2 运算结果
| N = 1e2 | 191.360411 | 5.858119 |
| N = 1e4 | 194.903941 | -5.814489 |
| N = 1e6 | 194.906195 | -5.816071 |
| N = 1e8 | 194.906195 | -5.816063 |
注:1)本篇内容均为对《MATLAB建模与仿真》(周品 赵新芬 编著,国防工业出版社)摘录与个人归纳总结,如需要更加详细了解,可阅读原书“第8章 随机模拟和统计分析”部分。
2)代码由chat gpt生成。
相关文章:
蒙特卡洛方法(Monte Carlo,MC)
目录 1 序言 2 Monte Carlo法计算积分 3 最优化计算Monte Carlo法 1 序言 蒙特卡罗方法(Monte Carlo)是由冯诺依曼和乌拉姆等人发明的,“蒙特卡罗”这个名字是出自摩纳哥的蒙特卡罗赌场,这个方法是一类基于概率的方法的统称。是一种应用随机数来进行…...

python学习笔记8-函数2
参数传递 传不可变对象 & 传可变对象 def func(b):print(id(a), a) #140737041872600 234print(id(b), b) #140737041872600 234a 234 func(a)def func(b):print(id(a), a) #1413554098560 [343]print(id(b), b) #1413554098560 [343]a [343] func(a)def func(b):b.appe…...

电商项目高级篇06-缓存
电商项目高级篇06-缓存 1、docker下启动redis2、项目整合redis3、redis改造三级分类业务 缓存 流程图: data cache.load(id);//从缓存加载数据 If(data null){ data db.load(id);//从数据库加载数据 cache.put(id,data);//保存到 cache 中 } return data;在我们…...

使用 `aircrack-ng`扫描、获取握手包
使用 aircrack-ng 工具集来扫描 5GHz WiFi 网络的过程与扫描 2.4GHz 网络类似,但需要注意一些特定的配置和命令。以下是一个详细的步骤指南,帮助你在 5GHz 频段上扫描 WiFi 网络并捕获握手包。 ### 前提条件 1. **操作系统**:通常在 Linux 系…...

基于大数据python 酒店数据分析可视化大屏系统(源码+LW+部署讲解+数据库+ppt)
!!!!!!!!! 很对人不知道选题怎么选 不清楚自己适合做哪块内容 都可以免费来问我 避免后期給自己答辩找麻烦 增加难度(部分学校只有一次答辩机会 没弄好就延迟…...

uniapp中父组件调用子组件方法
实现过程(setup语法糖形式下) 在子组件完成方法逻辑,并封装。在子组件中使用defineExpose暴露子组件的该方法。在父组件完成子组件ref的绑定。通过ref调用子组件暴露的方法。 子组件示例 <template> </template><script se…...
STL算法之set相关算法
STL一共提供了四种与set(集合)相关的算法,分别是并集(union)、交集(intersection)、差集(difference)、对称差集(symmetric difference)。 目录 set_union set_itersection set_difference set_symmetric_difference 所谓set,可细分为数学上定义的和…...

vscode中json文件的注释飘红
vscode的json文件 添加注释,提示json中不允许有注释,点编辑器最下面的json,如下图 然后选择如上图的json with comments就好了...

【微服务】SpringBoot 整合Redis Stack 构建本地向量数据库相似性查询
目录 一、前言 二、向量数据库介绍 2.1 什么是向量数据库 2.2 向量数据库特点 2.3 向量数据库使用场景 三、常用的向量数据库解决方案 3.1 Milvus 3.1.1 Milvus是什么 3.1.2 Milvus主要特点 3.2 Faiss 3.2.1 Faiss是什么 3.2.2 Faiss主要特点 3.3 Pinecone 3.3.1 …...

三:安装服务-controller node
一:工具、环境准备-controller node 二:OpenStack环境准备-controller node 三:安装服务-controller node 四:工具、环境准备-compute node 五:OpenStack环境准备-compute node 六:安装服务-compute node 七…...
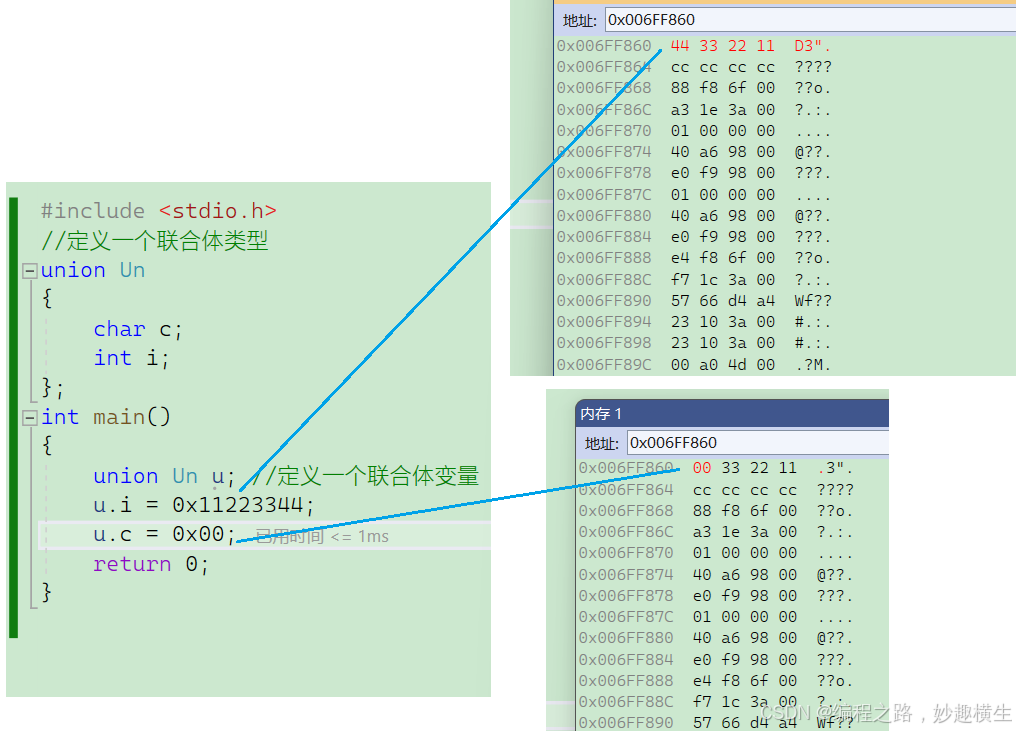
自定义类型: 结构体、枚举 、联合
目录 结构体 结构体类型的声明 匿名结构体 结构的自引用 结构体变量的定义和初始化 结构体成员变量的访问 结构体内存对齐 结构体传参 位段 位段类型的声明 位段的内存分配 位段的跨平台问题 位段的应用 枚举 枚举类型的定义 枚举的优点 联合体(共用体) 联合…...
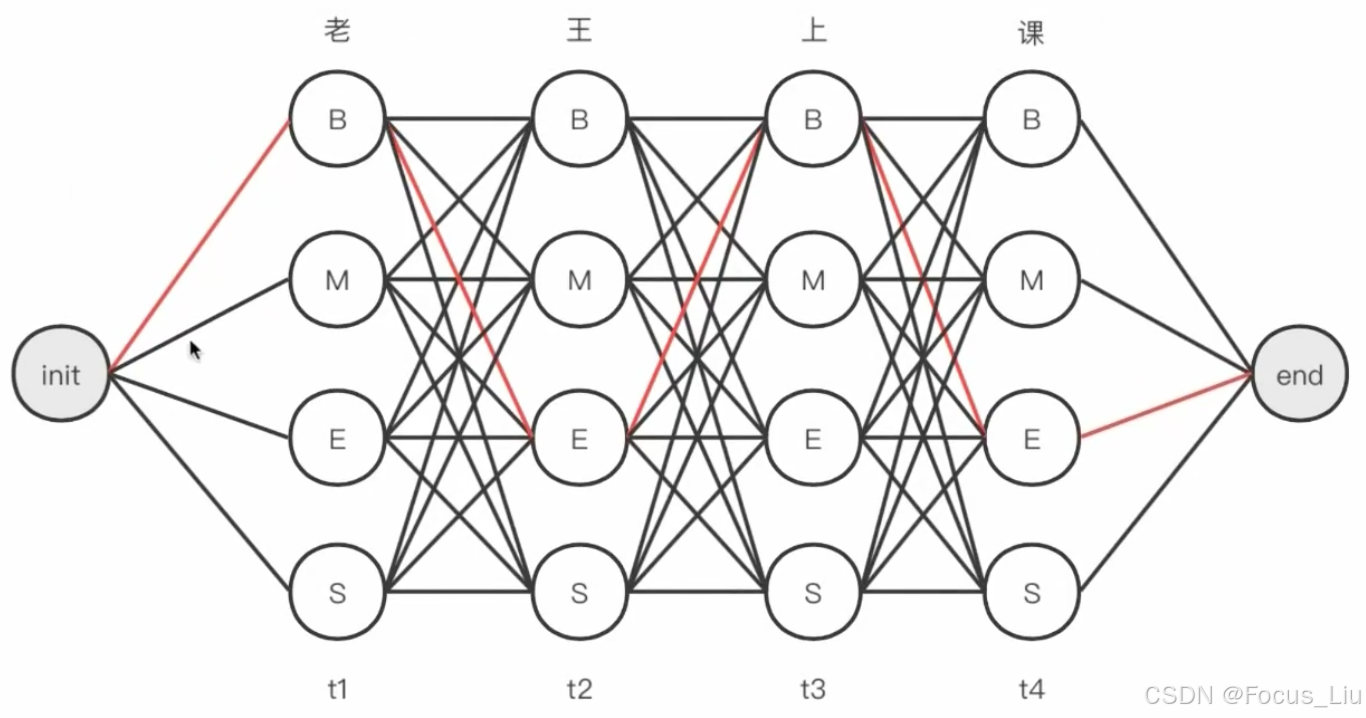
Bert+CRF的NER实战
CRF(条件随机场-Conditional Random Field) 原始本文:我在北京吃炸酱面 标注示例: 我O在O北B-PLA京I-PLA吃O炸B-FOOD酱I-FOOD面I-FOOD CRF: 目的:提出一些不可能出现的预测组合(例如I-PLA不能…...

永久停用PostgreSQL 归档功能
文章目录 引言永久停用归档功能归档的优势归档的劣势开启归档的情况关闭归档的情况see also引言 PostgreSQL 是一个开源的关系型数据库系统,支持数据归档(WAL),可以实现数据备份、恢复和灾难恢复等功能。在使用 PostgreSQL 的过程中,如果 PostgreSQL 数据库开启了归档(a…...
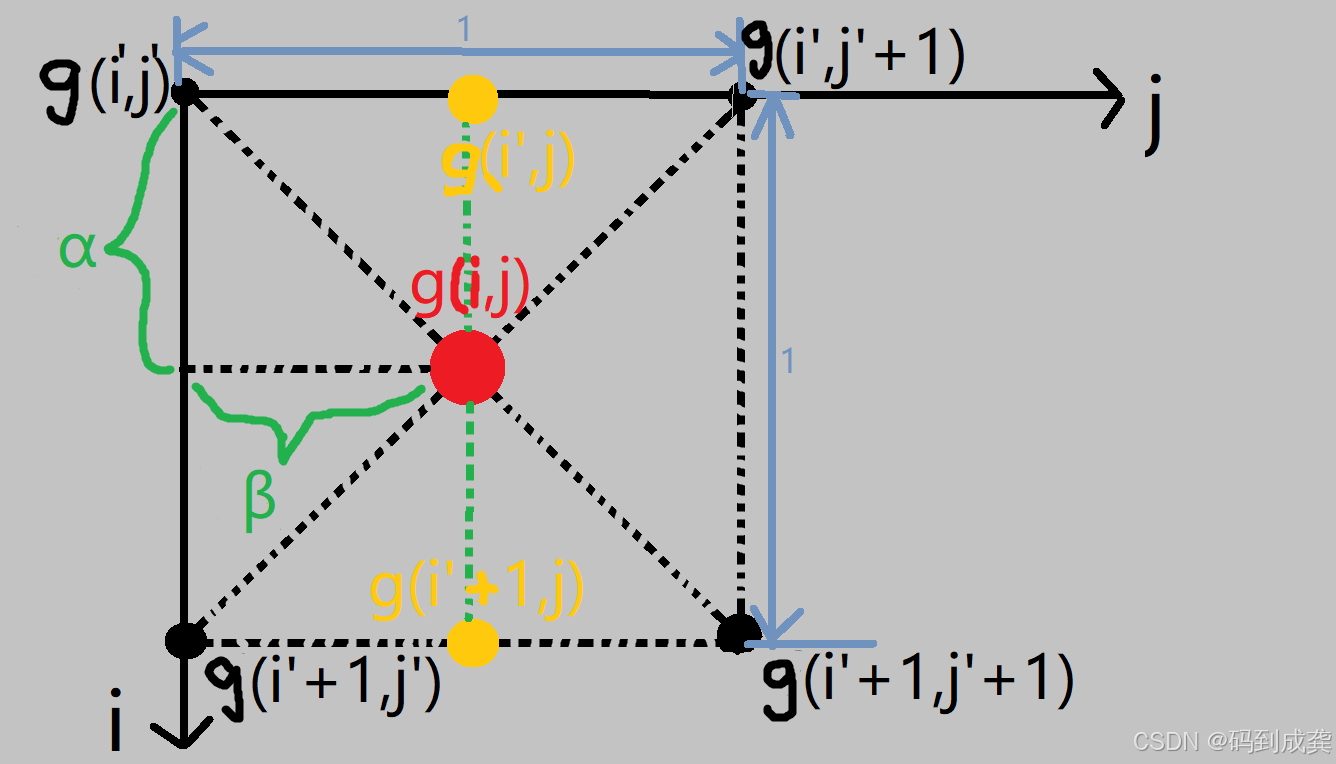
《数字图像处理基础》学习07-图像几何变换之最近邻插值法放大图像
目录 一,概念 二,题目及matlab实现 1,解题思路 2,matlab实现 1)matlab思路 2)完整代码 三,放大图像及matlab实现 一,概念 通过上一篇,我已经学习了使用最邻近插…...

pip安装库时报错(请求超时)
天行健,君子以自强不息;地势坤,君子以厚德载物。 每个人都有惰性,但不断学习是好好生活的根本,共勉! 文章均为学习整理笔记,分享记录为主,如有错误请指正,共同学习进步。…...

XPath表达式详解及其在Web开发中的应用
XPath(XML Path Language)是一种强大的查询语言,用于在XML文档中选择节点。由于HTML可以被视为一种特殊的XML,因此XPath同样适用于HTML文档。XPath允许开发者通过元素的层级结构和属性来选择节点或节点集合,这使得它成…...

Qt中Socket网络编程
文章目录 Qt中Socket网络编程服务器端客户端 Qt中Socket网络编程 这里就拿b站上爱编程的小丙的demo来做总结吧,首先要感谢成功带我入门的人:爱编程的小丙和程序员长风,这两个人是讲Socket编程我听懂的课555,接下来就总结一下Qt中…...

【05】Selenium+Python 两种文件上传方式(AutoIt)
上传文件的两种方式 一、input标签上传文件 可以用send_keys方法直接上传文件 示例代码 input标签上传文件import time from selenium import webdriver from chromedriver_py import binary_path # this will get you the path variable from selenium.webdriver.common.by i…...

Python网络编程
网络编程 Socket(套接字) socket 位于 网络协议中的 数据传输层、 该层 主要 可以通过 UDP 或者 TCP协议 实现 数据的传输 TCP 协议 VS UDP协议 tcp : 是一个 可靠的 ,面向 连接的协议。 数据在网络传输中 是安全的,不易丢失的。 TCP连接 在建立的时候&…...

openssl生成ca证书
常见CA文件夹 1、生成CA钥匙 openssl genrsa -out ./private/cakey.pem 2、生成CA自签名 openssl req -new -x509 -key ./private/cakey.pem -out ./cacert.crt -days 3650 3、生成http服务器私钥 openssl genrsa -out ./data/frontt.project.com.key 2048 4、CA给http服务器…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

Matlab实现任意伪彩色图像可视化显示
Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中,如何展示好看的实验结果图像非常重要!!! 1、灰度原始图像 灰度图像每个像素点只有一个数值,代表该点的亮度(或…...

当下AI智能硬件方案浅谈
背景: 现在大模型出来以后,打破了常规的机械式的对话,人机对话变得更聪明一点。 对话用到的技术主要是实时音视频,简称为RTC。下游硬件厂商一般都不会去自己开发音视频技术,开发自己的大模型。商用方案多见为字节、百…...
