Siknhorn算法介绍
SiknHorn算法是一个快速求解离散优化问题的经典算法,特别适用于计算离散分布之间的**最优传输(Optimal Transport)**距离;
最优传输问题介绍
计算两个概率分布 P 和 Q 之间的传输成本,通常表示为:
是传输代价矩阵
π 是联合分布(运输计划),满足边缘分布等于 P和 Q;
U(P,Q) 是所有满足边缘分布的有效运输计划的集合;
直接求解此问题的复杂度较高,为 。Sinkhorn算法通过在目标函数中引入正则化项(如Kullback-Leibler散度)将问题转化为更易解的形式.
Sinkhorn正则化的形式
引入熵正则化后,问题变为:
其中 ϵ>0 是正则化参数,用来控制正则化项的权重。此时的优化目标是凸的,可以通过迭代方法快速求解。
算法核心思想
Sinkhorn算法利用行列缩放的思想 (行列缩放的思想-CSDN博客),将优化问题转化为矩阵的归一化迭代:
初始化:构造一个权重矩阵 K,其元素为:
标量因子: 定义标量因子 u,v 来调整 K的行列和,使其分别等于分布 P和 Q:
迭代更新:
其中 / 表示逐元素相除.
重复迭代直到收敛。
算法步骤
输入:代价矩阵 C,分布 P,Q, 正则化参数 ϵ,收敛阈值 τ
初始化:设置 u=1(全为1的向量),计算 K。
循环:
检查收敛:判断 是否满足精度 τ。
精度 τ是一个用于判断算法是否收敛的阈值。它控制的是最终结果与目标分布之间的误差大小:
误差=
是当前矩阵的行和;
P 是目标行和;
是当前矩阵的列和;
Q是目标列和;
表示向量的范数(通常为 ℓ1 或 ℓ2 范数)。
输出:最终的传输计划 π 和传输成本。
import numpy as npdef sinkhorn_algorithm(C, r, c, epsilon=1e-3, max_iter=1000, tol=1e-6):"""Sinkhorn算法计算最优传输问题的近似解。参数:C (numpy.ndarray): 传输代价矩阵 (n, m)。r (numpy.ndarray): 源分布 (n,)。c (numpy.ndarray): 目标分布 (m,)。epsilon (float): 正则化参数,默认为 1e-3。max_iter (int): 最大迭代次数。tol (float): 收敛阈值,默认为 1e-6。返回:pi (numpy.ndarray): 近似的最优传输计划矩阵。transport_cost (float): 最优传输距离。"""# 确保分布为 numpy 数组并且是列向量形式r = np.array(r, dtype=np.float64)c = np.array(c, dtype=np.float64)# 初始化 K 矩阵,K[i, j] = exp(-C[i, j] / epsilon)K = np.exp(-C / epsilon)# 初始化缩放因子 u 和 vu = np.ones_like(r)v = np.ones_like(c)# 迭代更新 u 和 vfor iteration in range(max_iter):u_prev = u.copy() # 保存上一轮的 u 以判断收敛u = r / (K @ v) # 更新行缩放因子v = c / (K.T @ u) # 更新列缩放因子# 判断是否收敛if np.allclose(u, u_prev, atol=tol):break# 计算最终的传输计划矩阵 pipi = np.diag(u) @ K @ np.diag(v)# 计算最优传输成本transport_cost = np.sum(pi * C)return pi, transport_cost# 示例用法
if __name__ == "__main__":# 定义代价矩阵 (3x3)C = np.array([[4, 8, 6],[3, 7, 5],[2, 4, 6]])# 定义源分布和目标分布r = np.array([0.5, 0.3, 0.2]) # 源分布c = np.array([0.4, 0.4, 0.2]) # 目标分布# 调用 Sinkhorn 算法pi, cost = sinkhorn_algorithm(C, r, c, epsilon=1e-2, max_iter=500, tol=1e-6)# 输出结果print("传输计划矩阵 pi:")print(pi)print(f"最优传输距离: {cost}")
相关文章:
Siknhorn算法介绍
SiknHorn算法是一个快速求解离散优化问题的经典算法,特别适用于计算离散分布之间的**最优传输(Optimal Transport)**距离; 最优传输问题介绍 计算两个概率分布 P 和 Q 之间的传输成本,通常表示为: 是传输…...

群控系统服务端开发模式-应用开发-邮箱短信通道功能开发
邮箱短信通道主要是将邮箱及短信做归属的。具体见下图: 一、创建表 1、语句 CREATE TABLE cluster_control.nc_param_emailsms (id int(11) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 编号,email_id varchar(120) CHARACTER SET utf8 COLLATE utf8_general_ci NO…...

[docker中首次配置git环境]
11月没写东西,12月初赶紧水一篇。 刚开始搭建docker服务器时,网上找一堆指令配置好git后,再次新建容器后忘记怎么配了,,这次记录下。 一、git ssh指令法,该方法不用每次提交时输入密码 前期准备࿰…...

书生浦语·第四期作业合集
目录 1. Linux基础知识 1.1-Linux基础知识 1.在终端通过ssh 端口映射连接开发机 2. 创建helloworld.py 3.安装相关包并运行 4.端口映射并访问相关网页...

5G学习笔记之PRACH
即使是阴天,也要记得出门晒太阳哦 目录 1. 概述 2. PRACH Preamble 3. PRACH Preamble 类型 3.1 长前导码 3.2 短前导码 3.3 前导码格式与小区覆盖 4. PRACH时频资源 4.1 小区所有可用PRACH资源 4.2 SSB和RACH的关系 4.3 PRACH时频资源配置 1. 概述 随机接入…...

Ubuntu24.04配置DINO-Tracker
一、引言 记录 Ubuntu 配置的第一个代码过程 二、更改conda虚拟环境的默认安装路径 鉴于不久前由于磁盘空间不足引发的重装系统的惨痛经历,在新系统装好后当然要先更改虚拟环境的默认安装路径。 输入指令: conda info可能因为我原本就没有把 Anacod…...

抓包之查看websocket内容
写在前面 本文看下websocket抓包相关内容。 1:正文 websocket基础环境搭建参考这篇文章。 启动后,先看chrome的network抓包,这里我们直接使用is:running来过滤出websocket的请求: 可以清晰的看到发送的内容以及响应的内容。在…...

【Leetcode Top 100】21. 合并两个有序链表
问题背景 将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。 数据约束 两个链表的节点数目范围是 [ 0 , 50 ] [0, 50] [0,50] − 100 ≤ N o d e . v a l ≤ 100 -100 \le Node.val \le 100 −100≤Node.val≤100 l 1 l_1 …...

账本模型
05-账本模型 1 账本模型 1.1 传统线性增长模型 传统的 MySQL 等系统采用线性增长的日志模型,通过一个 Leader 和多个 Follower 进行状态同步。这种方式有单点的带宽瓶颈问题。 1.2 区块链共享账本模型 共享账本:树形增长。在去中心化网络中,…...

openwrt利用nftables在校园网环境下开启nat6 (ipv6 nat)
年初写过一篇openwrt在校园网环境下开启ipv6 nat的文章,利用ip6tables控制ipv6的流量。然而从OpenWrt22版本开始,系统内置的防火墙变为nftables,因此配置方法有所改变。本文主要参考了OpenWRT使用nftables实现IPv6 NAT 这篇文章。 友情提示 …...

24.12.02 Element
import { createApp } from vue // 引入elementPlus js库 css库 import ElementPlus from element-plus import element-plus/dist/index.css //中文语言包 import zhCn from element-plus/es/locale/lang/zh-cn //图标库 import * as ElementPlusIconsVue from element-plus/i…...
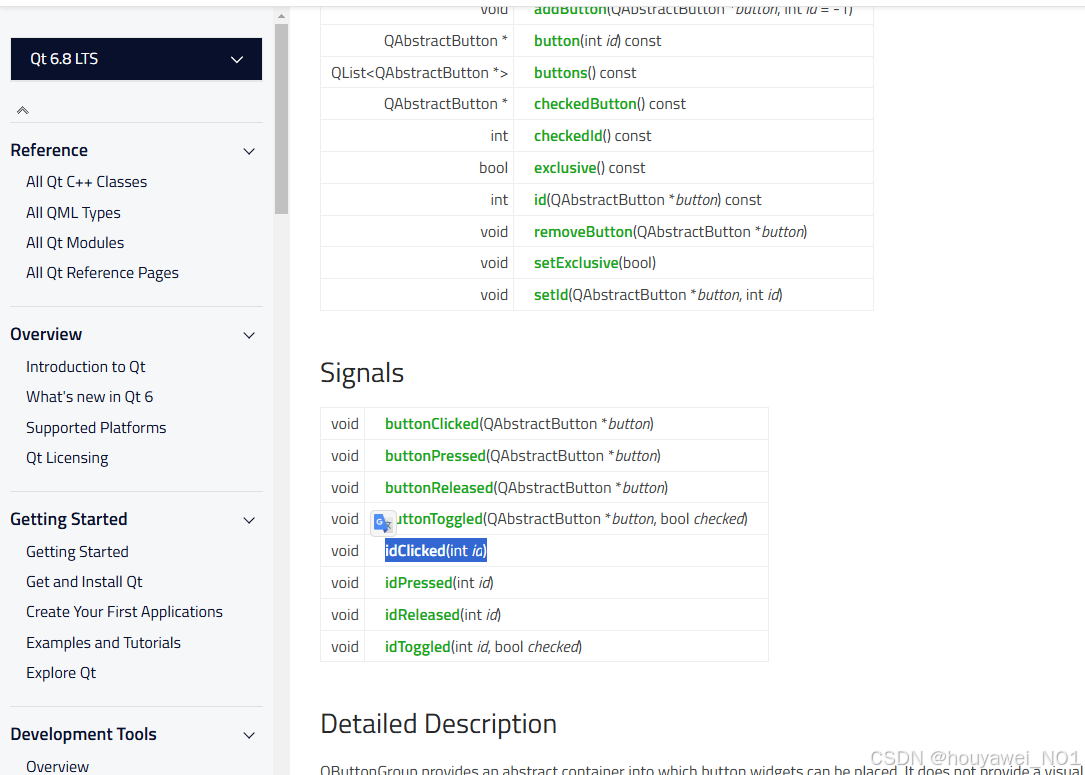
记录QT5迁移到QT6.8上的一些问题
经常看到有的同学说网上的教程都是假的,巴拉巴拉,看看人家发布时间,Qt官方的API都会有所变动,多搜索,多总结,再修改记录。 下次遇到问题多这样搜索 QT 4/5/6 xxx document,对比一下就知道…...

清理Linux/CentOS7根目录的思路
在使用Linux服务器过程中,经常会遇到磁盘空间不足的问题,好多应用默认安装在根目录下,记录一下如何找到问题所在,清理根目录(/) 1. 检查空间使用情况 1.1 查看分区占用: df -h输出࿱…...
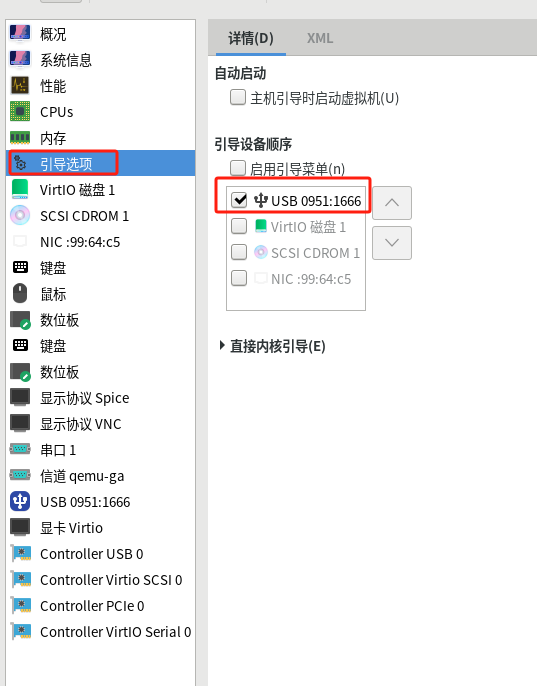
【LInux】kvm添加u盘启动引导
前提:要有一个u盘的启动盘 1、查看u盘设备信息 # lsusb ....忽略其他设备信息,查看到u盘设备 Bus 005 Device 005: ID 0951:1666 Kingston Technology DataTraveler 100 G3/G4/SE9 G2## 主要记住ID 0951:1666确认id为ID 0951:1666 2、修改配置文件 如…...
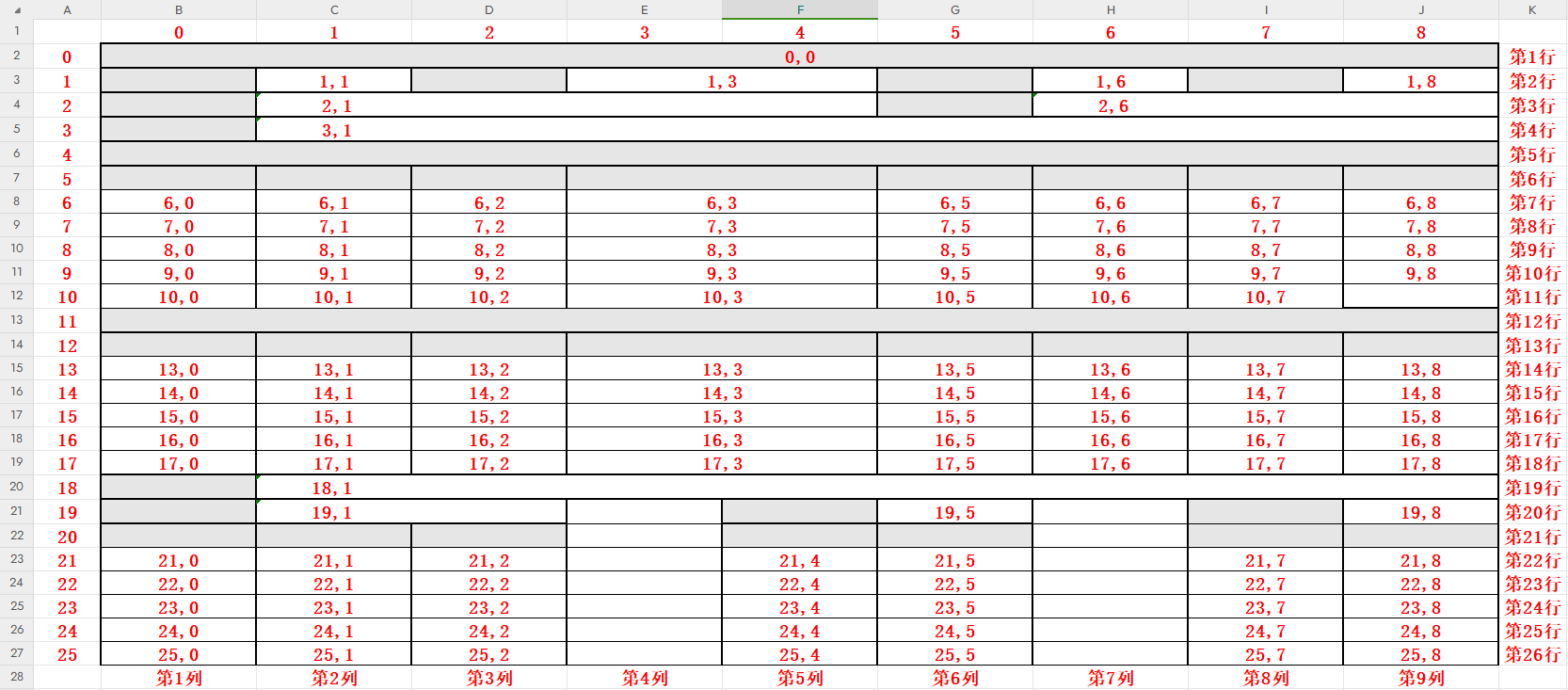
.net XSSFWorkbook 读取/写入 指定单元格的内容
方法如下: using NPOI.SS.Formula.Functions;using NPOI.SS.UserModel;using OfficeOpenXml.FormulaParsing.Excel.Functions.DateTime;using OfficeOpenXml.FormulaParsing.Excel.Functions.Numeric;/// <summary>/// 读取Excel指定单元格内容/// </summa…...

GaussDB(类似PostgreSQL)常用命令和注意事项
文章目录 前言GaussDB(类似PostgreSQL)常用命令和注意事项1. 连接到GaussDB数据库2. 查看当前数据库中的所有Schema3. 进入指定的Schema4. 查看Schema下的表、序列、视图5. 查看Schema下所有的表6. 查看表结构7. 开始事务8. 查询表字段注释9. 注意事项&a…...

【HM-React】02. React基础-下
React表单控制 受控绑定 概念:使用React组件的状态(useState)控制表单的状态 function App(){const [value, setValue] useState()return (<input type"text" value{value} onChange{e > setValue(e.target.value)}/>) …...
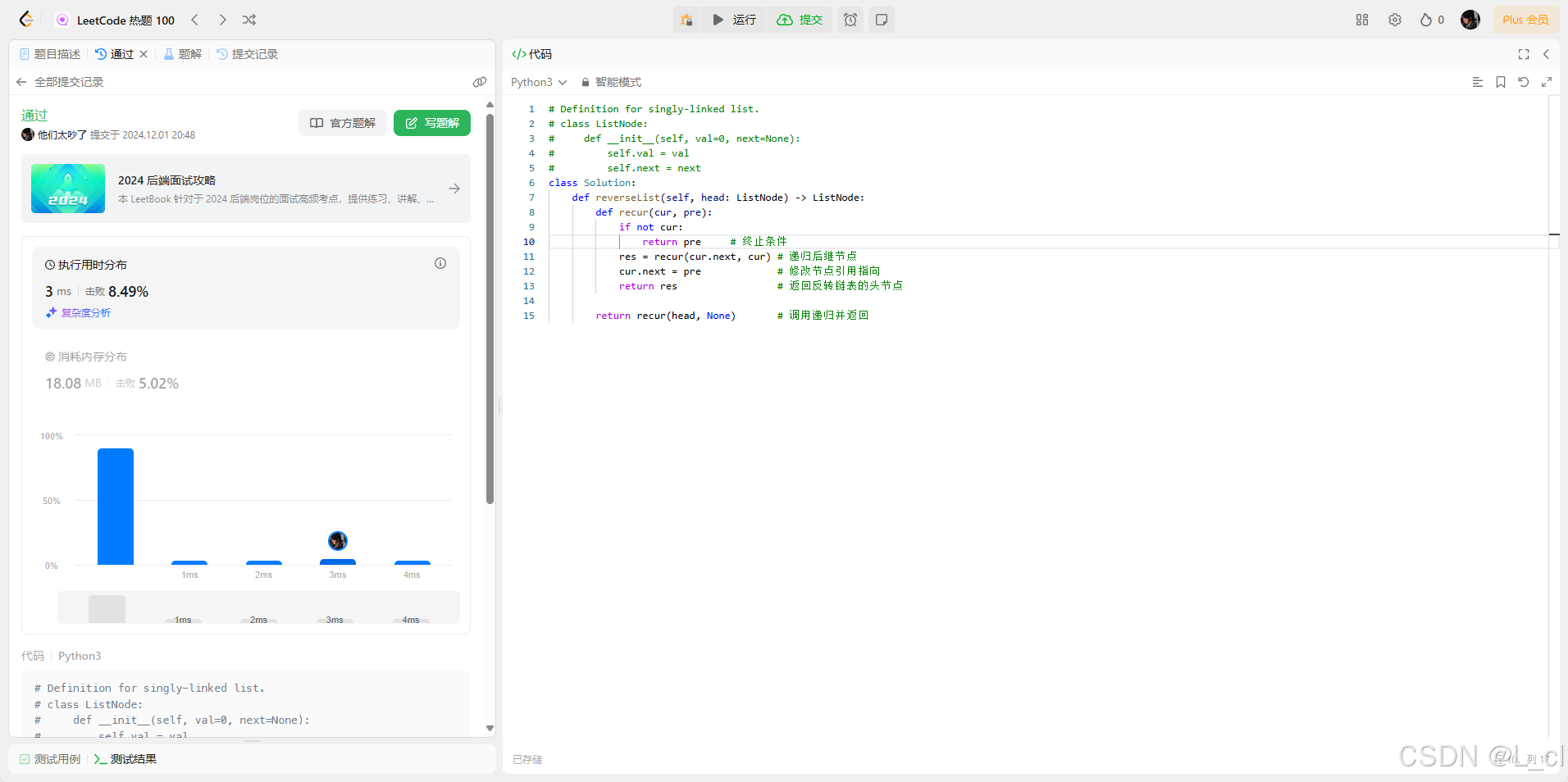
【力扣热题100】—— Day3.反转链表
你不会永远顺遂,更不会一直年轻,你太安静了,是时候出发了 —— 24.12.2 206. 反转链表 给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。 示例 1: 输入:head [1,2,3,4,5] 输出&…...
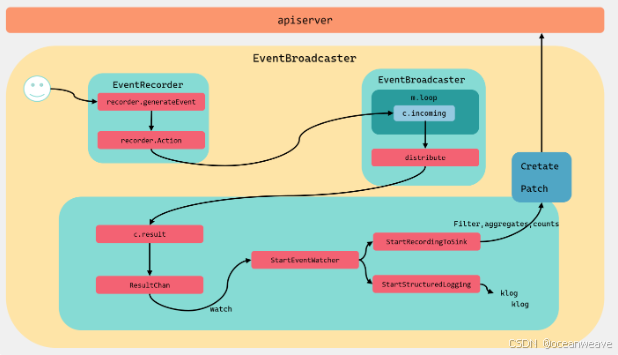
【k8s深入学习之 event 记录】初步了解 k8s event 记录机制
event 事件记录初始化 一般在控制器都会有如下的初始化函数,初始化 event 记录器等参数 1. 创建 EventBroadcaster record.NewBroadcaster(): 创建事件广播器,用于记录和分发事件。StartLogging(klog.Infof): 将事件以日志的形式输出。StartRecording…...

redhat 7.9配置阿里云yum源
1、mv /etc/yum.repos.d/*.repo /etc/yum.repos.d/backup/ 2、添加dns vim/etc/resolv.conf nameserver 8.8.8.8 nameserver 8.8.4.4 nameserver 114.114.114.114 #配置完先检查下通不通 3、vi /etc/yum/pluginconf.d/subscription-manager.conf # 将 “enabled1” 改为 “ena…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...
