2022高等代数上【南昌大学】
2022 高等代数
- 证明: p ( x ) p(x) p(x) 是不可约多项式的充要条件是对任意的多项式 f ( x ) , g ( x ) f(x), g(x) f(x),g(x),若 p ( x ) ∣ f ( x ) g ( x ) p(x) \mid f(x)g(x) p(x)∣f(x)g(x),则有 p ( x ) ∣ f ( x ) p(x) \mid f(x) p(x)∣f(x) 或 p ( x ) ∣ g ( x ) p(x) \mid g(x) p(x)∣g(x)。
⇒ \Rightarrow ⇒
当 p ( x ) p(x) p(x) 是不可约多项式,且 p ( x ) ∣ f ( x ) g ( x ) p(x) \mid f(x)g(x) p(x)∣f(x)g(x) ,若 p ( x ) ∤ f ( x ) p(x) \nmid f(x) p(x)∤f(x),则两多项式互素,即 ( p ( x ) , f ( x ) ) = 1 (p(x),f(x))=1 (p(x),f(x))=1,于是 p ( x ) ∣ g ( x ) p(x) \mid g(x) p(x)∣g(x)
⇐ \Leftarrow ⇐
若 p ( x ) p(x) p(x) 可约,设 p ( x ) = p 1 ( x ) p 2 ( x ) p(x)=p_1(x)p_2(x) p(x)=p1(x)p2(x) , ∂ ( p i ( x ) ) = deg p i ( x ) < deg p ( x ) = ∂ ( p ( x ) ) ( i = 1 , 2 ) \partial \left( p_i(x) \right) = \deg p_i(x) < \deg p(x) = \partial \left( p(x) \right)\,(i=1,2) ∂(pi(x))=degpi(x)<degp(x)=∂(p(x))(i=1,2) , p ( x ) ∣ p 1 ( x ) p 2 ( x ) p(x) \mid p_1(x)p_2(x) p(x)∣p1(x)p2(x) ,但 p ( x ) ∤ p 1 ( x ) p(x) \nmid p_1(x) p(x)∤p1(x), p ( x ) ∤ p 2 ( x ) p(x) \nmid p_2(x) p(x)∤p2(x)
- 计算行列式
∣ 2 n − 2 2 n − 1 − 2 ⋯ 2 3 − 2 2 2 − 2 3 n − 3 3 n − 1 − 3 ⋯ 3 3 − 3 3 2 − 3 ⋮ ⋮ ⋱ ⋮ ⋮ n n − n n n − 1 − n ⋯ n 3 − n n 2 − n ∣ . \begin{vmatrix} 2^n - 2 & 2^{n-1} - 2 & \cdots & 2^3 - 2 & 2^2 - 2 \\ 3^n - 3 & 3^{n-1} - 3 & \cdots & 3^3 - 3 & 3^2 - 3 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ n^n - n & n^{n-1} - n & \cdots & n^3 - n & n^2 - n \\ \end{vmatrix}. 2n−23n−3⋮nn−n2n−1−23n−1−3⋮nn−1−n⋯⋯⋱⋯23−233−3⋮n3−n22−232−3⋮n2−n .
法 1
∣ 2 n − 2 2 n − 1 − 2 ⋯ 2 2 − 2 3 n − 3 3 n − 1 − 3 ⋯ 3 2 − 3 ⋮ ⋮ ⋱ ⋮ n n − n n n − 1 − n ⋯ n 2 − n ∣ = ∣ 2 n − 1 ( 2 − 1 ) 2 n − 2 ( 2 − 1 ) ⋯ 2 ( 2 − 1 ) 3 n − 1 ( 3 − 1 ) 3 n − 2 ( 3 − 1 ) ⋯ 3 ( 3 − 1 ) ⋮ ⋮ ⋱ ⋮ n n − 1 ( n − 1 ) n n − 2 ( n − 1 ) ⋯ n ( n − 1 ) ∣ = ( n − 1 ) ! ∣ 2 n − 1 2 n − 2 ⋯ 2 3 n − 1 3 n − 2 ⋯ 3 ⋮ ⋮ ⋱ ⋮ n n − 1 n n − 2 ⋯ n ∣ = n ! ( n − 1 ) ! ∣ 2 n − 2 2 n − 3 ⋯ 1 3 n − 2 3 n − 3 ⋯ 1 ⋮ ⋮ ⋱ ⋮ n n − 2 n n − 3 ⋯ 1 ∣ = n ! ( n − 1 ) ! ( − 1 ) ( n − 1 ) ( n − 2 ) 2 ∏ 2 ≤ j < i ≤ n ( i − j ) = ( − 1 ) ( n − 1 ) ( n − 2 ) 2 ∏ k = 1 n k ! \begin{align*} \left| \begin{array}{cccc} {2^n - 2} & {2^{n - 1} - 2} & \cdots & {2^2 - 2} \\ {3^n - 3} & {3^{n - 1} - 3} & \cdots & {3^2 - 3} \\ \vdots & \vdots & \ddots & \vdots \\ {n^n - n} & {n^{n - 1} - n} & \cdots & {n^2 - n} \end{array} \right| &= \left| \begin{array}{cccc} {2^{n - 1} (2 - 1)} & {2^{n - 2} (2 - 1)} & \cdots & {2 (2 - 1)} \\ {3^{n - 1} (3 - 1)} & {3^{n - 2} (3 - 1)} & \cdots & {3 (3 - 1)} \\ \vdots & \vdots & \ddots & \vdots \\ {n^{n - 1} (n - 1)} & {n^{n - 2} (n - 1)} & \cdots & {n (n - 1)} \end{array} \right| \\ &= (n - 1)! \left| \begin{array}{cccc} {2^{n - 1}} & {2^{n - 2}} & \cdots & 2 \\ {3^{n - 1}} & {3^{n - 2}} & \cdots & 3 \\ \vdots & \vdots & \ddots & \vdots \\ {n^{n - 1}} & {n^{n - 2}} & \cdots & n \end{array} \right| \\ &= n! (n - 1)! \left| \begin{array}{cccc} {2^{n - 2}} & {2^{n - 3}} & \cdots & 1 \\ {3^{n - 2}} & {3^{n - 3}} & \cdots & 1 \\ \vdots & \vdots & \ddots & \vdots \\ {n^{n - 2}} & {n^{n - 3}} & \cdots & 1 \end{array} \right| \\ &= n! (n - 1)! \left( -1 \right)^{\frac{(n - 1)(n - 2)}{2}} \prod_{2 \le j < i \le n} (i - j) \\ &= \left( -1 \right)^{\frac{(n - 1)(n - 2)}{2}} \prod_{k = 1}^n k! \end{align*} 2n−23n−3⋮nn−n2n−1−23n−1−3⋮nn−1−n⋯⋯⋱⋯22−232−3⋮n2−n = 2n−1(2−1)3n−1(3−1)⋮nn−1(n−1)2n−2(2−1)3n−2(3−1)⋮nn−2(n−1)⋯⋯⋱⋯2(2−1)3(3−1)⋮n(n−1) =(n−1)! 2n−13n−1⋮nn−12n−23n−2⋮nn−2⋯⋯⋱⋯23⋮n =n!(n−1)! 2n−23n−2⋮nn−22n−33n−3⋮nn−3⋯⋯⋱⋯11⋮1 =n!(n−1)!(−1)2(n−1)(n−2)2≤j<i≤n∏(i−j)=(−1)2(n−1)(n−2)k=1∏nk!
法 2
∣ 2 n − 2 2 n − 1 − 2 ⋯ 2 3 − 2 2 2 − 2 3 n − 3 3 n − 1 − 3 ⋯ 3 3 − 3 3 2 − 3 ⋮ ⋮ ⋱ ⋮ ⋮ n n − n n n − 1 − n ⋯ n 3 − n n 2 − n ∣ = ∣ 1 1 1 ⋯ 1 1 0 2 n − 2 2 n − 1 − 2 ⋯ 2 3 − 2 2 2 − 2 0 3 n − 3 3 n − 1 − 3 ⋯ 3 3 − 3 3 2 − 3 ⋮ ⋮ ⋮ ⋱ ⋮ ⋮ 0 n n − n n n − 1 − n ⋯ n 3 − n n 2 − n ∣ = n ! ∣ 1 1 1 ⋯ 1 1 1 2 n − 1 2 n − 2 ⋯ 2 2 2 1 3 n − 1 3 n − 2 ⋯ 3 2 3 ⋮ ⋮ ⋮ ⋱ ⋮ ⋮ 1 n n − 1 n n − 2 ⋯ n 2 n ∣ = n ! ( − 1 ) ( n − 1 ) ( n − 2 ) 2 ∣ 1 1 1 ⋯ 1 1 1 2 2 2 ⋯ 2 n − 2 2 n − 1 1 3 3 2 ⋯ 3 n − 2 3 n − 1 ⋮ ⋮ ⋮ ⋱ ⋮ ⋮ 1 n n 2 ⋯ n n − 2 n n − 1 ∣ = ( − 1 ) ( n − 1 ) ( n − 2 ) 2 ∏ k = 1 n k ! \begin{align*} \left| \begin{array}{ccccc} {2^n - 2} & {2^{n - 1} - 2} & \cdots & {2^3 - 2} & {2^2 - 2} \\ {3^n - 3} & {3^{n - 1} - 3} & \cdots & {3^3 - 3} & {3^2 - 3} \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ {n^n - n} & {n^{n - 1} - n} & \cdots & {n^3 - n} & {n^2 - n} \end{array} \right| &= \left| \begin{array}{cccccc} 1 & 1 & 1 & \cdots & 1 & 1 \\ 0 & {2^n - 2} & {2^{n - 1} - 2} & \cdots & {2^3 - 2} & {2^2 - 2} \\ 0 & {3^n - 3} & {3^{n - 1} - 3} & \cdots & {3^3 - 3} & {3^2 - 3} \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & {n^n - n} & {n^{n - 1} - n} & \cdots & {n^3 - n} & {n^2 - n} \end{array} \right| \\ &= n! \left| \begin{array}{cccccc} 1 & 1 & 1 & \cdots & 1 & 1 \\ 1 & {2^{n - 1}} & {2^{n - 2}} & \cdots & {2^2} & 2 \\ 1 & {3^{n - 1}} & {3^{n - 2}} & \cdots & {3^2} & 3 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 1 & {n^{n - 1}} & {n^{n - 2}} & \cdots & {n^2} & n \end{array} \right| \\ &= n! \left( -1 \right)^{\frac{(n - 1)(n - 2)}{2}} \left| \begin{array}{cccccc} 1 & 1 & 1 & \cdots & 1 & 1 \\ 1 & 2 & {2^2} & \cdots & {2^{n - 2}} & {2^{n - 1}} \\ 1 & 3 & {3^2} & \cdots & {3^{n - 2}} & {3^{n - 1}} \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 1 & n & {n^2} & \cdots & {n^{n - 2}} & {n^{n - 1}} \end{array} \right| \\ &= \left( -1 \right)^{\frac{(n - 1)(n - 2)}{2}} \prod_{k = 1}^n k! \end{align*}
相关文章:

2022高等代数上【南昌大学】
2022 高等代数 证明: p ( x ) p(x) p(x) 是不可约多项式的充要条件是对任意的多项式 f ( x ) , g ( x ) f(x), g(x) f(x),g(x),若 p ( x ) ∣ f ( x ) g ( x ) p(x) \mid f(x)g(x) p(x)∣f(x)g(x),则有 p ( x ) ∣ f ( x ) p(x) \mid f(x) p(x)∣f(x) 或 p ( x ) ∣ g (…...
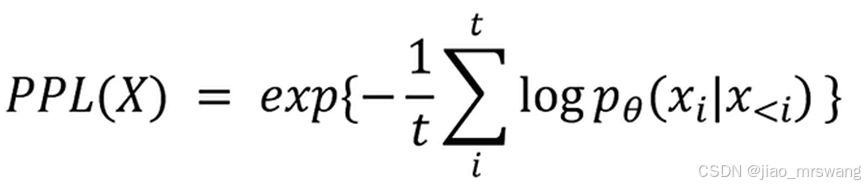
文本生成类(机器翻译)系统评估
在机器翻译任务中常用评价指标:BLEU、ROGUE、METEOR、PPL。 这些指标的缺点:只能反应模型输出是否类似于测试文本。 BLUE(Bilingual Evaluation Understudy):是用于评估模型生成的句子(candidate)和实际句子(referen…...
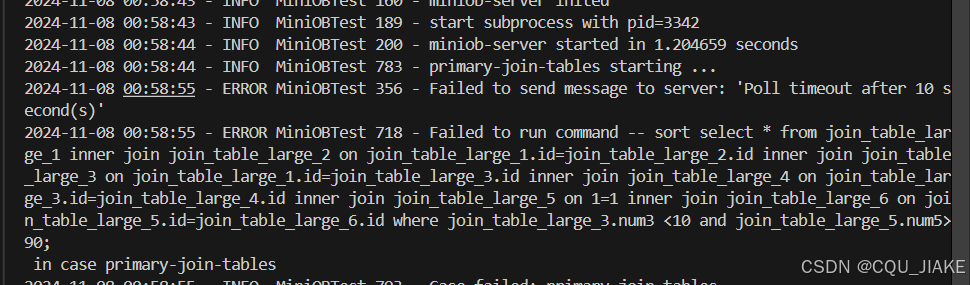
11.7【miniob】【debug】
这里的vector是实际值,而relation是指针,所以要解引用,*$1,并在最后调用其析构函数 emplace_back 和 push_back 都是用于在容器(如 std::vector)的末尾添加元素的方法,但它们的工作方式有所不同…...

OSHI 介绍与使用
OSHI 介绍 OSHI(Operating System and Hardware Information)是一个开源的Java库,用于从操作系统和硬件层面获取系统资源的详细信息。它提供了对操作系统、硬件、CPU、内存、磁盘、网络接口等多种信息的访问,且不依赖于平台特定的…...
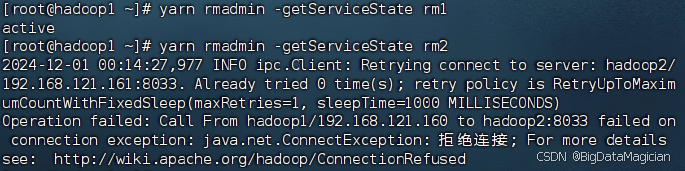
Hadoop生态圈框架部署(八)- Hadoop高可用(HA)集群部署
文章目录 前言一、部署规划二、Hadoop HA集群部署(手动部署)1. 下载hadoop2. 上传安装包2. 解压hadoop安装包3. 配置hadoop配置文件3.1 虚拟机hadoop1修改hadoop配置文件3.1.1 修改 hadoop-env.sh 配置文件3.3.2 修改 core-site.xml 配置文件3.3.3 修改 …...
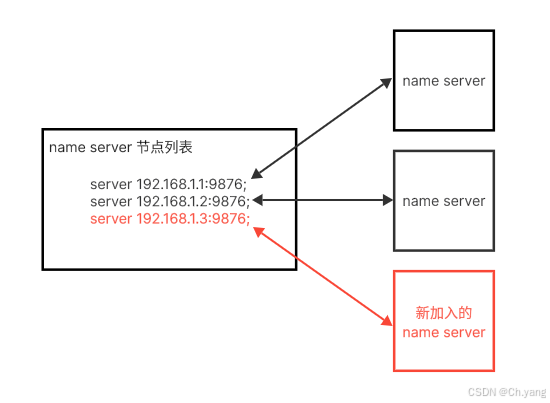
【RocketMQ】Name Server 无状态特点及如何让 Broker Consumer Producer 感知新节点
文章目录 前言1. Name Server 无状态特点2. Name Server 地址服务3. Name Server 手动配置后记 前言 看了 《RocketMQ 消息中间件实战派(上册)》前面一点,书中代码太多容易陷入细节。 这里简单描述下 RocketMQ Name Server 无状态表现在什么…...
蓝牙定位的MATLAB程序,四个锚点、三维空间
这段代码通过RSSI信号强度实现了在三维空间中的蓝牙定位,展示了如何使用锚点位置和测量的信号强度来估计未知点的位置。代码涉及信号衰减模型、距离计算和最小二乘法估计等基本概念,并通过三维可视化展示了真实位置与估计位置的关系。 目录 程序描述 运…...

机器学习--绪论
开启这一系列文章的初衷,是希望搭建一座通向机器学习世界的桥梁,为有志于探索这一领域的读者提供系统性指引和实践经验分享。随着人工智能和大数据技术的迅猛发展,机器学习已成为推动技术创新和社会变革的重要驱动力。从智能推荐系统到自然语…...
详解)
Unity 设计模式-命令模式(Command Pattern)详解
命令模式(Command Pattern)是一种行为型设计模式,它将请求封装成对象,从而使得可以使用不同的请求、队列或日志请求,以及支持可撤销的操作。命令模式通常包含四个主要角色:命令(Command…...

线程信号量 Linux环境 C语言实现
既可以解决多个同类共享资源的互斥问题,也可以解决简易的同步问题 头文件:#include <semaphore.h> 类型:sem_t 初始化:int sem_init(sem_t *sem, int pshared, unsigned int value); //程序中第一次对指定信号量调用p、v操…...
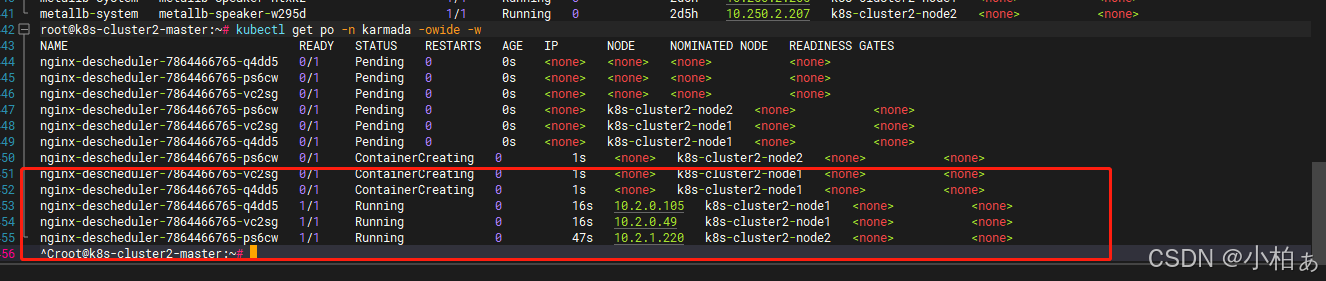
karmada-descheduler
descheduler规则 karmada-descheduler 定期检测所有部署,通常是每2分钟一次,并确定目标调度集群中无法调度的副本数量。它通过调用 karmada-scheduler-estimator 来完成这个过程。如果发现无法调度的副本,它将通过减少 spec.clusters 的配…...

【热门主题】000075 探索嵌入式硬件设计的奥秘
前言:哈喽,大家好,今天给大家分享一篇文章!并提供具体代码帮助大家深入理解,彻底掌握!创作不易,如果能帮助到大家或者给大家一些灵感和启发,欢迎收藏关注哦 💕 目录 【热…...

Android okhttp请求
下面是一个用 OkHttp 封装的 GET 请求方法,适用于 Android 项目。该方法包括基本的网络请求、错误处理,并支持通过回调返回结果。 封装 GET 请求的工具类 添加依赖 在你的 build.gradle 文件中,确保添加了 OkHttp 的依赖: imple…...

嵌入式蓝桥杯学习4 lcd移植
cubemx配置 复制前面配置过的文件 打开cubemx,将PB8,PB9配置为GPIO-Output。 点击GENERATE CODE. 文件移植 1.打开比赛提供的文件包,点击Inc文件夹 2.点击Inc文件夹。复制fonts.h和lcd.h,粘贴到我们自己的工程文件夹的bsp中(…...

电子应用设计方案-38:智能语音系统方案设计
智能语音系统方案设计 一、引言 智能语音系统作为一种便捷、自然的人机交互方式,正逐渐在各个领域得到广泛应用。本方案旨在设计一个高效、准确、功能丰富的智能语音系统。 二、系统概述 1. 系统目标 - 实现高准确率的语音识别和自然流畅的语音合成。 - 支持多种语…...

渗透测试:网络安全的深度探索
一、引言 在当今数字化时代,网络安全问题日益凸显。企业和组织面临着来自各种恶意攻击者的威胁,他们试图窃取敏感信息、破坏系统或进行其他恶意活动。渗透测试作为一种主动的安全评估方法,能够帮助企业发现潜在的安全漏洞,提高网…...

基于SpringBoot的“小区物业管理系统”的设计与实现(源码+数据库+文档+PPT)
基于SpringBoot的“小区物业管理系统”的设计与实现(源码数据库文档PPT) 开发语言:Java 数据库:MySQL 技术:SpringBoot 工具:IDEA/Ecilpse、Navicat、Maven 系统展示 系统功能结构图 个人信息界面图 费用信息管理…...

调试android 指纹遇到的坑
Android8以后版本 一、指纹服务不能自动 指纹服务fingerprintd(biometrics fingerprintservice),可以手动起来,但是在init.rc中无法启动。 解决办法: 1.抓取开机时kernel log ,确认我们的启动指纹服务的init.rc 文件有被init.c…...
剑指offer(专项突破)---字符串
总目录:剑指offer(专项突破)---目录-CSDN博客 1.字符串的基本知识 C语言中: 函数名功能描述strcpy(s1, s2)将字符串s2复制到字符串s1中,包括结束符\0,要求s1有足够空间容纳s2的内容。strncpy(s1, s2, n)…...

【springboot】 多数据源实现
文章目录 1. 引言:多数据源的必要性和应用场景**为什么需要多数据源?****应用场景** 2. Spring Boot中的数据源配置2.1 默认数据源配置简介2.2 如何在Spring Boot中配置多个数据源 3. 整合MyBatis与多数据源**配置MyBatis使用多数据源****Mapper接口的数…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...
