【题解】—— LeetCode一周小结48
🌟欢迎来到 我的博客 —— 探索技术的无限可能!
🌟博客的简介(文章目录)
【题解】—— 每日一道题目栏
上接:【题解】—— LeetCode一周小结47
25.网络延迟时间
题目链接:743. 网络延迟时间
有 n 个网络节点,标记为 1 到 n。
给你一个列表 times,表示信号经过 有向 边的传递时间。 times[i] = (ui, vi, wi),其中 ui 是源节点,vi 是目标节点, wi 是一个信号从源节点传递到目标节点的时间。
现在,从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号?如果不能使所有节点收到信号,返回 -1 。
示例 1:
输入:times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2
输出:2
示例 2:
输入:times = [[1,2,1]], n = 2, k = 1
输出:1
示例 3:
输入:times = [[1,2,1]], n = 2, k = 2
输出:-1
提示:
1 <= k <= n <= 100
1 <= times.length <= 6000
times[i].length == 3
1 <= ui, vi <= n
ui != vi
0 <= wi <= 100
所有 (ui, vi) 对都 互不相同(即,不含重复边)
题解:
方法:Dijkstra
class Solution {public int networkDelayTime(int[][] times, int n, int k) {final int INF = Integer.MAX_VALUE / 2; // 防止加法溢出int[][] g = new int[n][n]; // 邻接矩阵for (int[] row : g) {Arrays.fill(row, INF);}for (int[] t : times) {g[t[0] - 1][t[1] - 1] = t[2];}int maxDis = 0;int[] dis = new int[n];Arrays.fill(dis, INF);dis[k - 1] = 0;boolean[] done = new boolean[n];while (true) {int x = -1;for (int i = 0; i < n; i++) {if (!done[i] && (x < 0 || dis[i] < dis[x])) {x = i;}}if (x < 0) {return maxDis; // 最后一次算出的最短路就是最大的}if (dis[x] == INF) { // 有节点无法到达return -1;}maxDis = dis[x]; // 求出的最短路会越来越大done[x] = true; // 最短路长度已确定(无法变得更小)for (int y = 0; y < n; y++) {// 更新 x 的邻居的最短路dis[y] = Math.min(dis[y], dis[x] + g[x][y]);}}}
}26.交替组 I
题目链接:3206. 交替组 I
给你一个整数数组 colors ,它表示一个由红色和蓝色瓷砖组成的环,第 i 块瓷砖的颜色为 colors[i] :
colors[i] == 0 表示第 i 块瓷砖的颜色是 红色 。
colors[i] == 1 表示第 i 块瓷砖的颜色是 蓝色 。
环中连续 3 块瓷砖的颜色如果是 交替 颜色(也就是说中间瓷砖的颜色与它 左边 和 右边 的颜色都不同),那么它被称为一个 交替 组。
请你返回 交替 组的数目。
注意 ,由于 colors 表示一个 环 ,第一块 瓷砖和 最后一块 瓷砖是相邻的。
示例 1:
输入:colors = [1,1,1]
输出:0
解释:

示例 2:
输入:colors = [0,1,0,0,1]
输出:3
解释:

交替组包括:



提示:
3 <= colors.length <= 100
0 <= colors[i] <= 1
题解:
方法:遍历
class Solution {public int numberOfAlternatingGroups(int[] colors) {int k = 3;int n = colors.length;int ans = 0, cnt = 0;for (int i = 0; i < n << 1; ++i) {if (i > 0 && colors[i % n] == colors[(i - 1) % n]) {cnt = 1;} else {++cnt;}ans += i >= n && cnt >= k ? 1 : 0;}return ans;}
}
27.交替组 II
题目链接:3208. 交替组 II
给你一个整数数组 colors 和一个整数 k ,colors表示一个由红色和蓝色瓷砖组成的环,第 i 块瓷砖的颜色为 colors[i] :
colors[i] == 0 表示第 i 块瓷砖的颜色是 红色 。
colors[i] == 1 表示第 i 块瓷砖的颜色是 蓝色 。
环中连续 k 块瓷砖的颜色如果是 交替 颜色(也就是说除了第一块和最后一块瓷砖以外,中间瓷砖的颜色与它 左边 和 右边 的颜色都不同),那么它被称为一个 交替 组。
请你返回 交替 组的数目。
注意 ,由于 colors 表示一个 环 ,第一块 瓷砖和 最后一块 瓷砖是相邻的。
示例 1:
输入:colors = [0,1,0,1,0], k = 3
输出:3
解释:

交替组包括:



示例 2:
输入:colors = [0,1,0,0,1,0,1], k = 6
输出:2
解释:

交替组包括:


示例 3:
输入:colors = [1,1,0,1], k = 4
输出:0
解释:

提示:
3 <= colors.length <= 105
0 <= colors[i] <= 1
3 <= k <= colors.length
题解:
方法:动态规划
class Solution {public int numberOfAlternatingGroups(int[] colors, int k) {int n = colors.length;int ans = 0;int cnt = 0;for (int i = 0; i < n * 2; i++) {if (colors[i % n] == colors[(i + 1) % n]) {cnt = 0;}cnt++;if (i >= n && cnt >= k) {ans++;}}return ans;}
}
28.单调数组对的数目 I
题目链接:3250. 单调数组对的数目 I
给你一个长度为 n 的 正 整数数组 nums 。
如果两个 非负 整数数组 (arr1, arr2) 满足以下条件,我们称它们是 单调 数组对:
两个数组的长度都是 n 。
arr1 是单调 非递减 的,换句话说 arr1[0] <= arr1[1] <= … <= arr1[n - 1] 。
arr2 是单调 非递增 的,换句话说 arr2[0] >= arr2[1] >= … >= arr2[n - 1] 。
对于所有的 0 <= i <= n - 1 都有 arr1[i] + arr2[i] == nums[i] 。
请你返回所有 单调 数组对的数目。
由于答案可能很大,请你将它对 109 + 7 取余 后返回。
示例 1:
输入:nums = [2,3,2]
输出:4
解释:
单调数组对包括:
([0, 1, 1], [2, 2, 1])
([0, 1, 2], [2, 2, 0])
([0, 2, 2], [2, 1, 0])
([1, 2, 2], [1, 1, 0])
示例 2:
输入:nums = [5,5,5,5]
输出:126
提示:
1 <= n == nums.length <= 2000
1 <= nums[i] <= 50
题解:
方法:动态规划 + 前缀和优化
class Solution {public int countOfPairs(int[] nums) {final int mod = (int) 1e9 + 7;int n = nums.length;int m = Arrays.stream(nums).max().getAsInt();int[][] f = new int[n][m + 1];for (int j = 0; j <= nums[0]; ++j) {f[0][j] = 1;}int[] g = new int[m + 1];for (int i = 1; i < n; ++i) {g[0] = f[i - 1][0];for (int j = 1; j <= m; ++j) {g[j] = (g[j - 1] + f[i - 1][j]) % mod;}for (int j = 0; j <= nums[i]; ++j) {int k = Math.min(j, j + nums[i - 1] - nums[i]);if (k >= 0) {f[i][j] = g[k];}}}int ans = 0;for (int j = 0; j <= nums[n - 1]; ++j) {ans = (ans + f[n - 1][j]) % mod;}return ans;}
}
29.单调数组对的数目 II
题目链接:3251. 单调数组对的数目 II
给你一个长度为 n 的 正 整数数组 nums 。
如果两个 非负 整数数组 (arr1, arr2) 满足以下条件,我们称它们是 单调 数组对:
两个数组的长度都是 n 。
arr1 是单调 非递减 的,换句话说 arr1[0] <= arr1[1] <= … <= arr1[n - 1] 。
arr2 是单调 非递增 的,换句话说 arr2[0] >= arr2[1] >= … >= arr2[n - 1] 。
对于所有的 0 <= i <= n - 1 都有 arr1[i] + arr2[i] == nums[i] 。
请你返回所有 单调 数组对的数目。
由于答案可能很大,请你将它对 109 + 7 取余 后返回。
示例 1:
输入:nums = [2,3,2]
输出:4
解释:
单调数组对包括:
([0, 1, 1], [2, 2, 1])
([0, 1, 2], [2, 2, 0])
([0, 2, 2], [2, 1, 0])
([1, 2, 2], [1, 1, 0])
示例 2:
输入:nums = [5,5,5,5]
输出:126
提示:
1 <= n == nums.length <= 2000
1 <= nums[i] <= 1000
题解:
方法:动态规划 + 前缀和优化
class Solution {public int countOfPairs(int[] nums) {final int mod = (int) 1e9 + 7;int n = nums.length;int m = Arrays.stream(nums).max().getAsInt();int[][] f = new int[n][m + 1];for (int j = 0; j <= nums[0]; ++j) {f[0][j] = 1;}int[] g = new int[m + 1];for (int i = 1; i < n; ++i) {g[0] = f[i - 1][0];for (int j = 1; j <= m; ++j) {g[j] = (g[j - 1] + f[i - 1][j]) % mod;}for (int j = 0; j <= nums[i]; ++j) {int k = Math.min(j, j + nums[i - 1] - nums[i]);if (k >= 0) {f[i][j] = g[k];}}}int ans = 0;for (int j = 0; j <= nums[n - 1]; ++j) {ans = (ans + f[n - 1][j]) % mod;}return ans;}
}
30.判断是否可以赢得数字游戏
题目链接:3232. 判断是否可以赢得数字游戏
给你一个 正整数 数组 nums。
Alice 和 Bob 正在玩游戏。在游戏中,Alice 可以从 nums 中选择所有个位数 或 所有两位数,剩余的数字归 Bob 所有。如果 Alice 所选数字之和 严格大于 Bob 的数字之和,则 Alice 获胜。
如果 Alice 能赢得这场游戏,返回 true;否则,返回 false。
示例 1:
输入:nums = [1,2,3,4,10]
输出:false
解释:
Alice 不管选个位数还是两位数都无法赢得比赛。
示例 2:
输入:nums = [1,2,3,4,5,14]
输出:true
解释:
Alice 选择个位数可以赢得比赛,所选数字之和为 15。
示例 3:
输入:nums = [5,5,5,25]
输出:true
解释:
Alice 选择两位数可以赢得比赛,所选数字之和为 25。
提示:
1 <= nums.length <= 100
1 <= nums[i] <= 99
题解:
class Solution {public boolean canAliceWin(int[] nums) {int s = 0;for (int x : nums) {s += x < 10 ? x : -x;}return s != 0;}
}
2024.12
1.N 皇后
题目链接:51. N 皇后
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。
示例 1:
输入:n = 4
输出:[[“.Q…”,“…Q”,“Q…”,“…Q.”],[“…Q.”,“Q…”,“…Q”,“.Q…”]]
解释:如上图所示,4 皇后问题存在两个不同的解法。 示例 2:
输入:n = 1
输出:[[“Q”]]
提示:
1 <= n <= 9
题解:
方法:递归 回溯
class Solution {public List<List<String>> solveNQueens(int n) {List<List<String>> ans = new ArrayList<>();int[] queens = new int[n]; // 皇后放在 (r,queens[r])boolean[] col = new boolean[n];boolean[] diag1 = new boolean[n * 2 - 1];boolean[] diag2 = new boolean[n * 2 - 1];dfs(0, queens, col, diag1, diag2, ans);return ans;}private void dfs(int r, int[] queens, boolean[] col, boolean[] diag1, boolean[] diag2, List<List<String>> ans) {int n = col.length;if (r == n) {List<String> board = new ArrayList<>(n); // 预分配空间for (int c : queens) {char[] row = new char[n];Arrays.fill(row, '.');row[c] = 'Q';board.add(new String(row));}ans.add(board);return;}// 在 (r,c) 放皇后for (int c = 0; c < n; c++) {int rc = r - c + n - 1;if (!col[c] && !diag1[r + c] && !diag2[rc]) { // 判断能否放皇后queens[r] = c; // 直接覆盖,无需恢复现场col[c] = diag1[r + c] = diag2[rc] = true; // 皇后占用了 c 列和两条斜线dfs(r + 1, queens, col, diag1, diag2, ans);col[c] = diag1[r + c] = diag2[rc] = false; // 恢复现场}}}
}
下接:【题解】—— LeetCode一周小结49
相关文章:

【题解】—— LeetCode一周小结48
🌟欢迎来到 我的博客 —— 探索技术的无限可能! 🌟博客的简介(文章目录) 【题解】—— 每日一道题目栏 上接:【题解】—— LeetCode一周小结47 25.网络延迟时间 题目链接:743. 网络延迟时间 …...

040集——CAD中放烟花(CAD—C#二次开发入门)
效果如下: 单一颜色的烟花: 渐变色的火花: namespace AcTools {public class HH{public static TransientManager tm TransientManager.CurrentTransientManager;public static Random rand new Random();public static Vector3D G new V…...

一文理解多模态大语言模型——下
作者:Sebastian Raschka 博士, 翻译:张晶,Linux Fundation APAC Open Source Evangelist 编者按:本文并不是逐字逐句翻译,而是以更有利于中文读者理解的目标,做了删减、重构和意译,…...

ROS2创建 base 包用于其他模块的参数配置和头文件依赖
Demo 背景 ROS2项目开发中存在以下需求:有多个包需要读取一些共同的配置项(以txt或者yaml形式存在),且依赖于一些公用的utils工具代码(C)。Solution: 创建一个 base_config 包来“存放” 配置文件和公用的头文件。gitee address: Gitee/CDal…...

自然语言处理期末试题汇总
建议自己做,写完再来对答案。答案可能存在极小部分错误,不保证一定正确。 一、选择题 1-10、C A D B D B C D A A 11-20、A A A C A B D B B A 21-30、B C C D D A C A C B 31-40、B B B C D A B B A A 41-50、B D B C A B B B B C 51-60、A D D …...
——计算机网路篇)
前端热门面试题目(四)——计算机网路篇
计算机网络常见面试题: 计算机网络面试(一) 计算机网络面试(二) 计算机网络速成: 计算机网络速成一 计算机网络速成二 计算机网络速成三 2. HTTP 1.0 和 2.0 的区别 连接复用: HTTP/1.0 使用短连…...

kubenetes流水线实施清单
整体实施方案概述 创建命名空间(Namespace):创建一个专用于 CI/CD 的命名空间 cicd。配置 Secrets: Git SSH 密钥(分别为 Maven 和 npm 项目)Docker Registry 凭证(Kaniko)SMTP 凭证…...

Redis4——持久化与集群
Redis4——持久化与集群 本文讲述了1.redis在内存占用达到限制后的key值淘汰策略;2.redis主从复制原理;3.redis的哨兵模式;4.redis集群模式。 1. 淘汰策略 设置过期时间 expire key <timeout>只能对主hash表中的键设置过期时间。 查…...

【LeetCode: 94. 二叉树的中序遍历 + 栈】
🚀 算法题 🚀 🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀 🌲 越难的东西,越要努力坚持,因为它具有很高的价值,算法就是这样✨ 🌲 作者简介:硕风和炜,…...

Python系列 - MQTT协议
Python系列 - MQTT协议 资源连接 MQTT的介绍和应用场景的示例说明 一、什么是MQTT 百度关于MQTT的介绍如下: MQTT(消息队列遥测传输)是ISO 标准(ISO/IEC PRF 20922)下基于发布订阅范式的消息协议。它工作在 TCP/IP协议之上,是为硬件性能低下的远程设…...

同时在github和gitee配置密钥
同时在github和gitee配置密钥 1. 生成不同的 SSH 密钥 为每个平台生成单独的 SSH 密钥。 # 为 GitHub 生成密钥(默认文件路径为 ~/.ssh/github_id_rsa) ssh-keygen -t rsa -b 4096 -C "your_github_emailexample.com" -f ~/.ssh/github_id_…...
Runway 技术浅析(六):文本到视频(Text-to-Video)
1. 核心组件与工作原理 1.1 自然语言处理(NLP) 1.1.1 文本解析与语义理解 文本到视频的第一步是将用户输入的自然语言文本解析为机器可理解的语义信息。Runway 使用预训练的 NLP 模型,如 GPT-3 和 BERT,这些模型通过大规模文本数…...
云计算vspere 安装过程
1 材料的准备 1 安装虚拟机 vmware workstation 2 安装esxi 主机 3 在esxi 主机上安装windows 2018 dns 服务器 4 在虚拟机上安装windows 2018 服务器 6 安装vcenter 5 登入界面测试 这里讲一下,由于部署vspere 需要在windows 2012 服务器上部…...

QT 实现QStackedWidget切换页面右移动画
1.实现效果 以下是一个QStackedWidget,放了两个QPushButton在上面,点击切换不同的界面。 为了方便查看动画特效,设置了每个界面的背景图片。 2.实现思路 首先截取当前界面的图片,渲染到一个QLabel上,然后设置QPropertyAnimation动画,动画的作用对象就是这个QLabel,不断…...
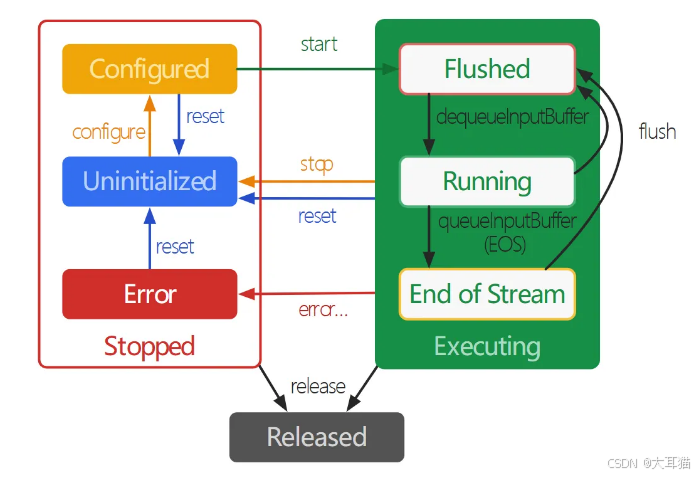
Android Camera2采集并编码为H.264
前言 本篇博文主要讲述的是基于Android原生MediaCodec通过Camera2 API进行图像数据采集并编码为H.264的实现过程,如果对此感兴趣的不妨驻足观看,也欢迎大家大家对本文中描述不当或者不正确的地方进行指正。如果对于Camera2预览还不熟悉的可以观看博主上…...

DHCP和DNS
DHCP(动态主机配置协议)和DNS(域名系统)是计算机网络中两个重要的协议,它们在网络的管理和使用中发挥着关键作用。 DHCP(动态主机配置协议) 基本功能 自动分配IP地址:DHCP允许网…...

ONES 功能上新|ONES Project 甘特图再度升级
ONES Project 甘特图支持展示工作项标题、进度百分比、依赖关系延迟时间等信息。 应用场景: 在使用甘特图规划项目任务、编排项目计划时,可以对甘特图区域进行配置,展示工作项的工作项标题、进度百分比以及依赖关系延迟时间等维度,…...

<工具 Claude Desktop> 配置 MCP server 连接本地 SQLite, 本机文件夹(目录) 网络驱动器 Windows 11 系统
也是在学习中... 起因: 抖音博客 艾克AI分享 他的视频 #143《Claude开源MCP彻底打破AI的信息孤岛》 提到: Claude开源的MCP太强了,视频后面是快速演示,反正看了好几遍也没弄明白。菜单都不一样,感觉用的不是同一家 Claude. 探…...

GIT的使用方法以及汉化方法
1.下载git软件,可以从官网下载 下载后默认安装即可。 2.找到一个文件夹,或者直接打开gitbash gitbash可以使用cd指令切换目录的 打开后输入 git clone https:[git仓库的网页]即可克隆仓库 就是这个地址 克隆后即可使用代码 如果忘记了命令可以使用 -…...

公因子的数目
给你两个正整数 a 和 b ,返回 a 和 b 的 公 因子的数目。 如果 x 可以同时整除 a 和 b ,则认为 x 是 a 和 b 的一个 公因子 。 输入:a 12, b 6 输出:4 解释:12 和 6 的公因子是 1、2、3、6 。 class Solution {pu…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

