切比雪夫不等式:方差约束下的概率估计
切比雪夫不等式:方差约束下的概率估计
背景
在概率分析中,切比雪夫不等式是一个常用的工具,它通过引入随机变量的 方差信息,给出了偏离均值的概率界限。这一不等式是对 马尔科夫不等式 的自然扩展,结合了更丰富的分布信息。通过它,我们可以更精确地描述随机变量的偏差行为。
核心思想
切比雪夫不等式旨在刻画以下概率:
P ( ∣ X − μ ∣ ≥ t ) \mathbb{P}(|X - \mu| \geq t) P(∣X−μ∣≥t)
其中, μ = E [ X ] \mu = \mathbb{E}[X] μ=E[X] 是随机变量 X X X 的期望, t > 0 t > 0 t>0 是阈值。为了进行更紧密的估计,引入 X X X 的方差 σ 2 = E [ ( X − μ ) 2 ] \sigma^2 = \mathbb{E}[(X - \mu)^2] σ2=E[(X−μ)2]。
切比雪夫不等式表明:
P ( ∣ X − μ ∣ ≥ t ) ≤ σ 2 t 2 . \mathbb{P}(|X - \mu| \geq t) \leq \frac{\sigma^2}{t^2}. P(∣X−μ∣≥t)≤t2σ2.
这一结果的直观意义是:随机变量偏离均值的概率与方差成正比,与偏差阈值的平方成反比。当 t t t 增大时,偏离概率迅速下降。
从马尔科夫不等式的扩展到切比雪夫不等式
马尔科夫不等式扩展回顾
回顾马尔科夫不等式扩展:给定一个非负随机变量 X X X 和一个单调递增的非负函数 g g g,我们有:
P ( X ≥ t ) = P ( g ( X ) ≥ g ( t ) ) ≤ E [ g ( X ) ] g ( t ) , g ( t ) > 0. \mathbb{P}(X \geq t) = \mathbb{P}(g(X) \geq g(t)) \leq \frac{\mathbb{E}[g(X)]}{g(t)}, \quad g(t) > 0. P(X≥t)=P(g(X)≥g(t))≤g(t)E[g(X)],g(t)>0.
这一形式可以推广到许多场景,具体证明可以参考我的博客 马尔科夫不等式扩展:非线性函数下的概率上界。
切比雪夫不等式的推导
在切比雪夫不等式中,我们让随机变量的偏差 Z = ∣ X − μ ∣ Z = |X - \mu| Z=∣X−μ∣,并选择 g ( x ) = x 2 g(x) = x^2 g(x)=x2。此时:
P ( ∣ X − μ ∣ ≥ t ) = P ( Z ≥ t ) = P ( g ( Z ) ≥ g ( t ) ) ≤ E [ g ( Z ) ] g ( t ) . \mathbb{P}(|X - \mu| \geq t) = \mathbb{P}(Z \geq t) = \mathbb{P}(g(Z) \geq g(t)) \leq \frac{\mathbb{E}[g(Z)]}{g(t)}. P(∣X−μ∣≥t)=P(Z≥t)=P(g(Z)≥g(t))≤g(t)E[g(Z)].
对于 g ( x ) = x 2 g(x) = x^2 g(x)=x2,我们有:
g ( Z ) = Z 2 = ( X − μ ) 2 , g ( t ) = t 2 . g(Z) = Z^2 = (X - \mu)^2, \quad g(t) = t^2. g(Z)=Z2=(X−μ)2,g(t)=t2.
因此:
P ( ∣ X − μ ∣ ≥ t ) ≤ E [ ( X − μ ) 2 ] t 2 . \mathbb{P}(|X - \mu| \geq t) \leq \frac{\mathbb{E}[(X - \mu)^2]}{t^2}. P(∣X−μ∣≥t)≤t2E[(X−μ)2].
注意到 E [ ( X − μ ) 2 ] \mathbb{E}[(X - \mu)^2] E[(X−μ)2] 就是 X X X 的方差 σ 2 \sigma^2 σ2,最终得到:
P ( ∣ X − μ ∣ ≥ t ) ≤ σ 2 t 2 . \mathbb{P}(|X - \mu| \geq t) \leq \frac{\sigma^2}{t^2}. P(∣X−μ∣≥t)≤t2σ2.
例子:投资收益的概率估算
假设你投资一个项目 X X X,它的年平均收益是 5 % 5\% 5%(即 E [ X ] = 0.05 \mathbb{E}[X] = 0.05 E[X]=0.05),年收益的方差为 Var ( X ) = σ 2 = 0.01 \text{Var}(X) = \sigma^2 = 0.01 Var(X)=σ2=0.01。你想知道收益超过期望值 50 % 50\% 50%(即 ∣ X − E [ X ] ∣ ≥ 0.5 |X - \mathbb{E}[X]| \geq 0.5 ∣X−E[X]∣≥0.5)的概率有多大。
使用马尔科夫不等式估算
首先,根据前面马尔科夫不等式,我们可以得到结果
P ( X ≥ 0.5 ) ≤ 0.05 0.5 = 0.1. \mathbb{P}(X \geq 0.5) \leq \frac{0.05}{0.5} = 0.1. P(X≥0.5)≤0.50.05=0.1.
即,收益超过 50 % 50\% 50% 的概率不会超过 10 % 10\% 10%。
马尔科夫不等式:一个快速的概率上界工具-CSDN博客
使用切比雪夫不等式估算
切比雪夫不等式考虑了收益的偏离范围,即:
P ( ∣ X − E [ X ] ∣ ≥ t ) ≤ σ 2 t 2 . \mathbb{P}(|X - \mathbb{E}[X]| \geq t) \leq \frac{\sigma^2}{t^2}. P(∣X−E[X]∣≥t)≤t2σ2.
这里的 t t t 是收益偏离期望值的阈值,因此 t = 0.5 − 0.05 = 0.45 t = 0.5 - 0.05 = 0.45 t=0.5−0.05=0.45,代入 σ 2 = 0.01 \sigma^2 = 0.01 σ2=0.01:
P ( ∣ X − E [ X ] ∣ ≥ 0.45 ) ≤ 0.01 0.4 5 2 ≈ 0.049. \mathbb{P}(|X - \mathbb{E}[X]| \geq 0.45) \leq \frac{0.01}{0.45^2} \approx 0.049. P(∣X−E[X]∣≥0.45)≤0.4520.01≈0.049.
即,收益偏离 50 % 50\% 50% 的概率不会超过 4.9 % 4.9\% 4.9%。
对比与分析
-
概率上界的精度
- 使用马尔科夫不等式得到的概率上界是 10 % 10\% 10%,而使用切比雪夫不等式后,概率上界下降到了 4.9 % 4.9\% 4.9%。
- 切比雪夫不等式利用了方差信息,给出了更紧的概率界限。
-
适用范围
- 马尔科夫不等式只需要知道随机变量的均值,适用于所有非负随机变量,因此更通用。
- 切比雪夫不等式需要额外的方差信息,因此对分布的要求更高,但界限更精确。
-
解释意义
- 马尔科夫不等式的结果相对宽松,因为它只利用了均值信息,假设更大的分布范围。
- 切比雪夫不等式通过引入方差,更好地描述了随机变量的波动特性。
特点与不足
优点
- 利用方差信息:相比马尔科夫不等式,切比雪夫不等式通过引入方差,得到了更紧的概率上界。
- 适用性广:只需知道均值和方差,无需任何额外的分布假设。
- 直观性:通过与方差和偏差的关系,定量描述了概率的变化。
缺点
- 上界仍然宽松:实际概率往往远小于不等式给出的界限。
- 不考虑分布形状:切比雪夫不等式无法充分利用随机变量的分布信息。
进一步延伸
- 更紧的界限:如果随机变量具有更详细的信息(如分布的对称性或独立性),可以使用更高级的不等式,如赫夫丁不等式或切尔诺夫界。
- 特殊分布的分析:对于某些特定分布,如正态分布,可以通过分布函数直接计算偏差概率,从而获得更精确的估计。
小结
切比雪夫不等式是从马尔科夫不等式出发,通过引入方差,提供了一个更紧密的概率界限。它在随机变量分析中具有广泛的应用,是概率界限工具箱中的一件基础工具。然而,在实际场景中,如果能够获取更多的分布特征,使用更高级的不等式往往能带来更好的结果。
在后续内容中,我们将进一步探讨如 Chernoff Bound(切尔诺夫界) 这样的工具,如何实现对偏差概率的更精确控制。
相关文章:

切比雪夫不等式:方差约束下的概率估计
切比雪夫不等式:方差约束下的概率估计 背景 在概率分析中,切比雪夫不等式是一个常用的工具,它通过引入随机变量的 方差信息,给出了偏离均值的概率界限。这一不等式是对 马尔科夫不等式 的自然扩展,结合了更丰富的分布…...

使用CancellationTokenSource来控制长时间sql查询中断
前端 <!-- 透明的覆盖层,显示在页面上方,包含进度条 --><Grid Visibility"{Binding IsLoading}" Background"Transparent" HorizontalAlignment"Stretch" VerticalAlignment"Stretch" ZIndex"1&…...

小红薯最新x-s 算法补环境教程12-06更新(下)
在上一篇文章中已经讲了如何去定位x-s生成的位置,本篇文章就直接开始撸代码吧 如果没看过的话可以看:小红薯最新x-s算法分析12-06(x-s 56)(上)-CSDN博客 1、获取加密块代码 首先来到参数生成的位置&…...

wazuh-modules-sca
wazuh中安全配置评估模块主线程执行wm_sca_main最后在wm_sca_start中循环执行,不会返回 // Module main function. It wont return #ifdef WIN32 DWORD WINAPI wm_sca_main(void *arg) {wm_sca_t *data (wm_sca_t *)arg; #else void * wm_sca_main(wm_sca_t * dat…...

Uniapp的App环境下使用Map获取缩放比例
概述 目前我试过的就是你用vue后缀是拿不到比例的你可以用nvue当然uniapp的uvue应该是更加可以的我使用的是高德所以你得在高德的后台声请原生的Android的key才可以如果是vue3的开发模式的话不用使用this来获取当前对象使用scale对象来接受和改变缩放比例会比较友好然后直接走…...

微信小程序配置less并使用
1.在VScode中下载Less插件 2.在微信小程序中依次点击如下按钮 选择 从已解压的扩展文件夹安装… 3.选中刚在vscode中下载安装的插件文件 如果没有修改过插件的安装目录,一般是在c盘下C:\用户\用户名.vscode\extensions\mrcrowl.easy-less-2.0.2 我的路径是…...

“全面支持公路数字化转型升级四大任务”视频孪生解决方案
数字经济的加速布局,对交通领域数字化转型、智能化升级提出明确要求。2024年上半年,为深入贯彻落实中共中央、国务院关于加快建设交通强国、数字中国等决策部署,推进公路水路交通基础设施数字转型、智能升级、融合创新,加快发展新…...

顶顶通电话机器人开发接口对接大语言模型之实时流TTS对接介绍
大语言模型一般都是流式返回文字,如果等全部文字返回了一次性去TTS,那么延迟会非常严重,常用的方法就是通过标点符号断句,返回了一句话就提交给TTS。随着流TTS的出现,就可以直接把大模型返回的文字灌给流TTS࿰…...

P3379 【模板】最近公共祖先(LCA)
【模板】最近公共祖先(LCA) https://www.luogu.com.cn/problem/P3379 题目描述 如题,给定一棵有根多叉树,请求出指定两个点直接最近的公共祖先。 输入格式 第一行包含三个正整数 N , M , S N,M,S N,M,S,分别表示…...

2030. gitLab A仓同步到B仓
文章目录 1 A 仓库备份 到 B 仓库2 B 仓库修改main分支的权限 1 A 仓库备份 到 B 仓库 #!/bin/bash# 定义变量 REPO_DIR"/home/xhome/opt/git_sync/zz_xx_xx" # 替换为你的本地库A的实际路径 REMOTE_ORIGIN"http://192.168.1.66:8181/zzkj_software/zz_xx_xx.…...
源代码并和eclipse做关联)
网易博客旧文-----如何在WINDOWS下载安卓(android)源代码并和eclipse做关联
如何在WINDOWS下载安卓(android)源代码并和eclipse做关联 2013-02-05 17:27:16| 分类: 安卓开发 | 标签: |举报 |字号大中小 订阅 编写安卓程序时,有时想看看安卓某些类的实现,但默认情况下环境是不带的。…...

MATLAB中axes函数用法
目录 语法 说明 示例 在图窗中定位多个坐标区 将坐标区设置为当前坐标区 在选项卡上创建坐标区 axes函数的功能是创建笛卡尔坐标区。 语法 axes axes(Name,Value) axes(parent,Name,Value) ax axes(___) axes(cax) 说明 axes 在当前图窗中创建默认的笛卡尔坐标区&…...
)
构建 Java Web 应用程序:实现简单的增删查改(Mysql)
简介 本教程将指导您如何使用Java Servlet和JSP技术构建一个简单的Web应用程序。该应用程序将包括用户注册、登录、注销(删除用户信息)、修改密码以及根据性别查询用户信息等功能。我们将使用MySQL数据库来存储用户数据。 环境准备 Java Development …...

3d行政区划-中国地图
前言 技术调研:做底代码平台的3d行政区组件 写的demo 效果图: 实现的功能项 地标、打点、飞线、three.js 3d 中国地图的一些基础配置补充 geo中国地图文件获取 其他项:包 "dependencies": {"d3": "^7.9.0","d3-…...

适合存储时序数据的数据库和存储系统
时序数据的存储通常要求高效地处理大量按时间排序的数据,同时支持快速查询、实时分析和高并发写入。以下是一些适合存储时序数据的数据库和存储系统: 1. InfluxDB 概述:InfluxDB 是一个开源的时序数据库,专门为处理时序数据而设…...
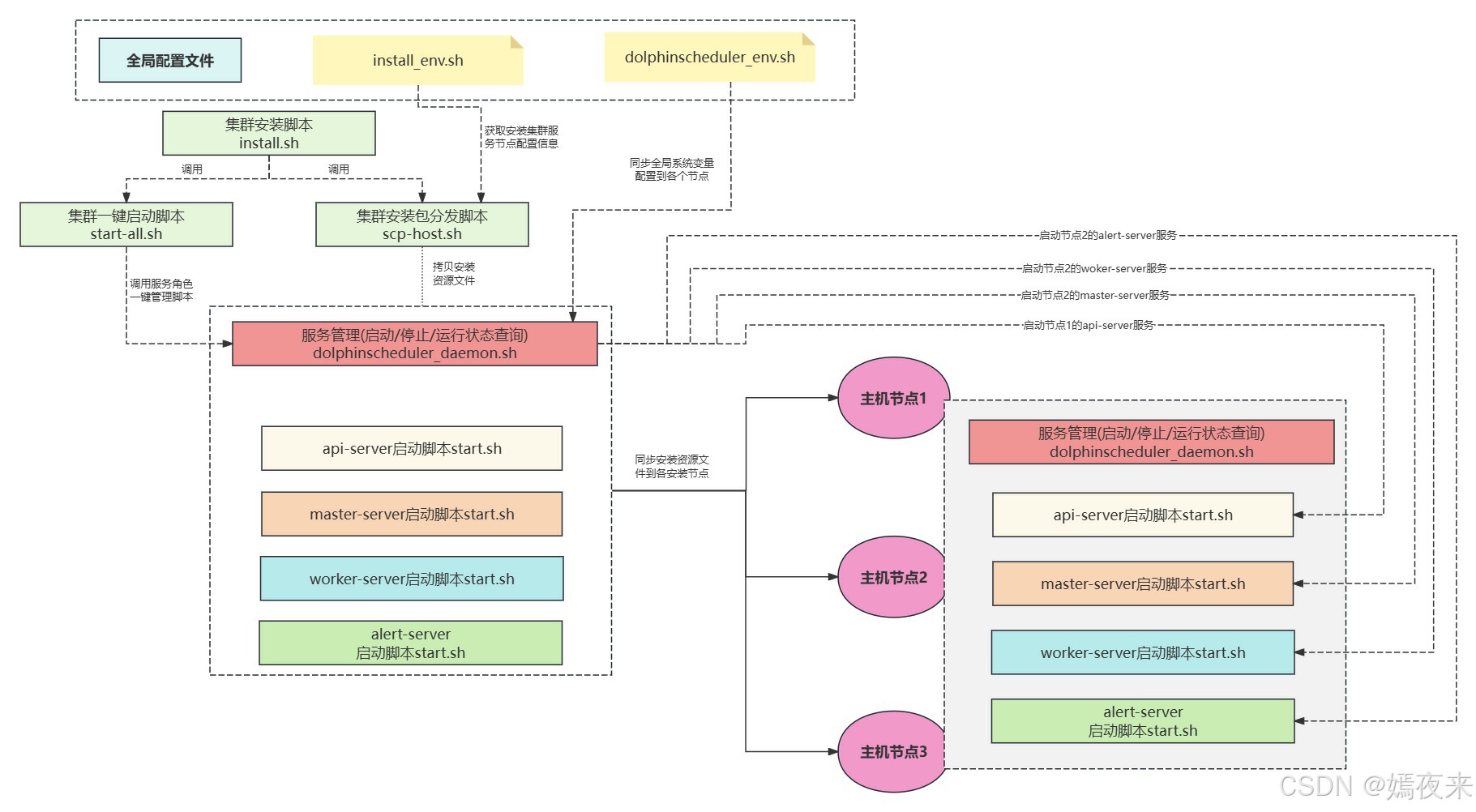
dolphinscheduler集群服务一键安装启动实现流程剖析
1.dolphinscheduler的安装部署 dolphinscheduler服务的安装部署都是非常简单的,因为就服务本身而言依赖的服务并不多。 mysql / postgresql。由于需要进行元数据及业务数据的持久化存储所以需要依赖于数据库服务,数据库服务支持mysql、postgresql等&am…...

深入了解Linux —— 学会使用vim编辑器
前言 学习了Linux中的基本指令也理解了权限这一概念,但是我们怎么在Linux下写代码呢? 本篇就来深入学习Linux下的vim编辑器;学会在Linux下写代码。 软件包管理器 1. 软件包? 在Linux下安装软件,通常是下载程序的源码…...

C05S01-Web基础和HTTP协议
一、Web基础 1. Web相关概念 1.1 URL URL(Uniform Resource Locator,统一资源定位符),是一种用于在互联网上标识和定位资源的标准化地址,提供了一种访问互联网上特定资源的方法。URL的基本格式如下所示:…...

MIT工具课第六课任务 Git基础练习题
如果您之前从来没有用过 Git,推荐您阅读 Pro Git 的前几章,或者完成像 Learn Git Branching 这样的教程。重点关注 Git 命令和数据模型相关内容; 相关内容整理链接:Linux Git新手入门 git常用命令 Git全面指南:基础概念…...

计算机网络安全
从广义来说,凡是涉及到网络上信息的机密性、报文完整性、端点鉴别等技术和理论都是网络安全的研究领域。 机密性指仅有发送方和接收方能理解传输报文的内容,而其他未授权用户不能解密(理解)该报文报文完整性指报文在传输过程中不…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...
