day57回文子串_最长回文子序列
力扣647.回文子串
题目链接:https://leetcode.cn/problems/palindromic-substrings/
思路
dp数组含义
dp[i][j]:以s[i]为开头,s[j]为结尾的子串是否是回文子串
递推公式
子串范围为[i,j],当s[i]==s[j]时,有三种情况:
(1)i==j,如[a],dp[i][j]=true,同时计数器res++;
(2)j=i+1,如[a,a],dp[i][j]=true,同时计数器res++;
(3)j-i>1,那么就需要判断子串内部,即[i+1,j-1]范围内是否是回文子串,如果是,则dp[i][j]=true;否则为false。
初始化
初始化为false
遍历顺序
由递推公式可知,dp[i][j]由dp[i+1][j-1]推导而来,所以要从底往上,从左到右遍历。
打印数组
返回计数器res。
完整代码
class Solution {public int countSubstrings(String s) {boolean[][] dp = new boolean[s.length()][s.length()];int res = 0;for (int i = s.length()-1; i >= 0; i--) {for (int j = i; j < s.length(); j++) {if(s.charAt(i) == s.charAt(j)){if(j - i <= 1) {dp[i][j] = true;res++;}else if (dp[i+1][j-1] == true){dp[i][j] = true;res++;}}}}return res;}
}
力扣516.最长回文子序列
题目链接:https://leetcode.cn/problems/longest-palindromic-subsequence/
思路
本题和回文子串的区别是:子序列是不要求连续的,可以删除字符!
dp数组含义
dp[i][j]:在[i,j]范围内的最长回文子序列的长度
递推公式
(1)s[i]==s[j]时,dp[i][j] = dp[i+1][j-1]+2,这个很好理解,+2是加上两端的字符
(2)s[i]!=s[j]时,说明两端字符同时加进去时不能构成回文字符串,所以考虑两种情况:1.放左边的,不放边的:dp[i][j]=dp[i][j-1];2.放右边的,不放左边的:dp[i][j]=dp[i+1][j]。取二者最大值
初始化
由递推公式dp[i][j] = dp[i+1][j-1]+2可知,i和j不能相等。所以初始化时,i=j即一个字符串的回文长度为1.其余为0
遍历顺序
和回文子串同理
打印数组
根据dp数组的含义,返回dp[0][s.length()-1]
完整代码
class Solution {public int longestPalindromeSubseq(String s) {int[][] dp = new int[s.length()][s.length()];for (int i = 0; i < s.length(); i++) {dp[i][i] = 1;}for (int i = s.length()-1; i >= 0; i--) {for (int j = i+1; j < s.length(); j++) {if (s.charAt(i) == s.charAt(j)){dp[i][j] = dp[i+1][j-1]+2;}else {dp[i][j] = Math.max(dp[i+1][j],dp[i][j-1]);}}}return dp[0][s.length()-1];}
}
相关文章:

day57回文子串_最长回文子序列
力扣647.回文子串 题目链接:https://leetcode.cn/problems/palindromic-substrings/ 思路 dp数组含义 dp[i][j]:以s[i]为开头,s[j]为结尾的子串是否是回文子串 递推公式 子串范围为[i,j],当s[i]s[j]时,有三种情况࿱…...

Element UI框架学习篇(二)
Element UI框架学习篇(二) 1 整体布局 1.1 前提说明 el-container标签里面的标签默认是从左往右排列,若想要从上往下排列,只需要写el-header或者el-footer就行了 <el-container>:外层容器 <el-header>:顶栏容器。 <el-aside>&#…...
【C++】类与对象(上)
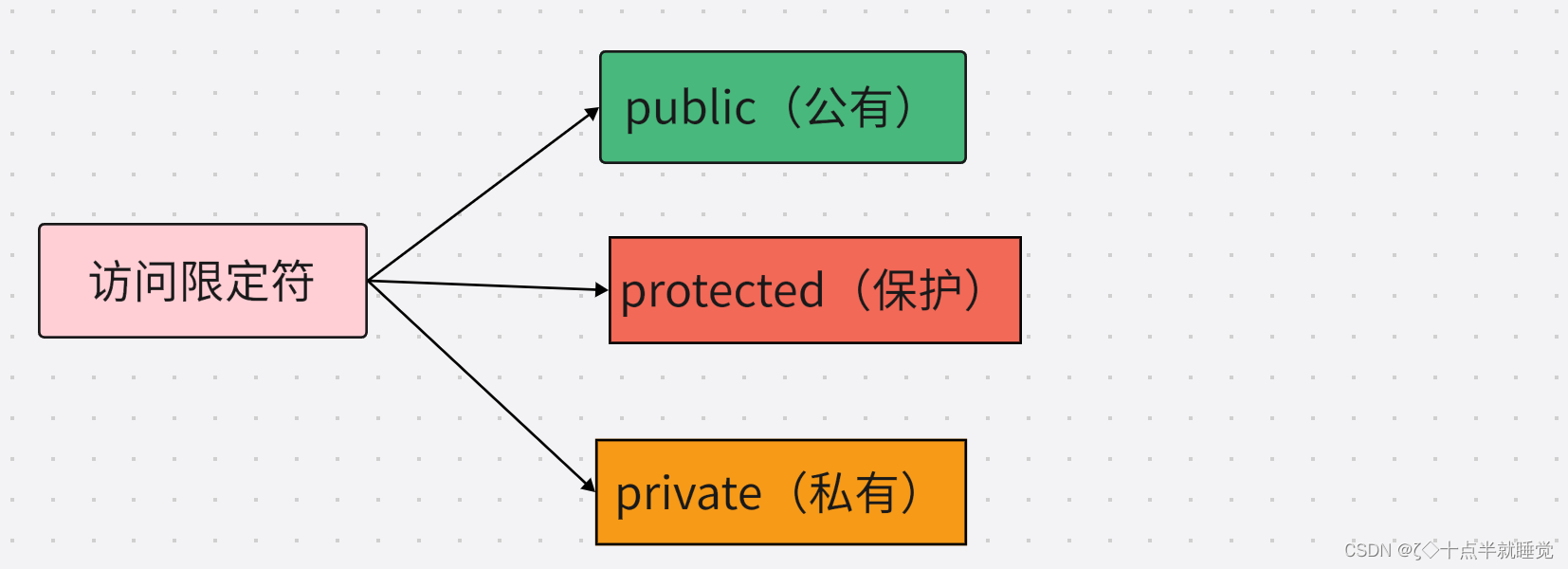
文章目录一、面向过程和面向对象初步认识二、类的引入三、类的定义四、类的访问限定符及封装①访问限定符②封装五、类的作用域六、类的实例化七、类对象模型①如何计算类对象大小②类对象的存储方式③结构体中内存对齐规则八、this指针①this指针的引出②this指针的特性一、面…...
Leetcode.1797 设计一个验证系统
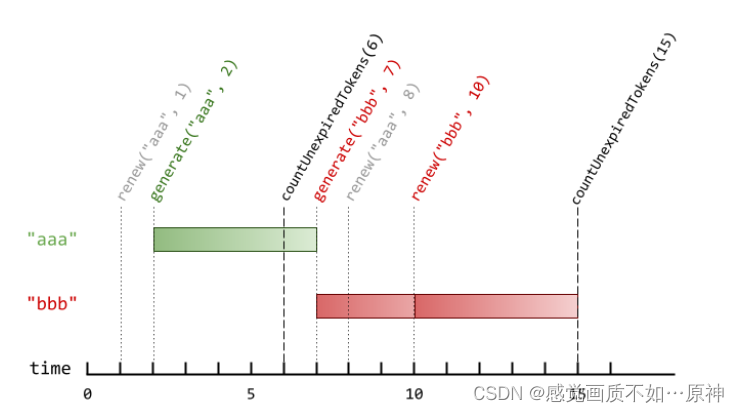
题目链接 Leetcode.1797 设计一个验证系统 Rating : 1534 题目描述 你需要设计一个包含验证码的验证系统。每一次验证中,用户会收到一个新的验证码,这个验证码在 currentTime时刻之后 timeToLive秒过期。如果验证码被更新了,那么它会在 curr…...

Kaldi - 数据文件准备
文章目录数据文件准备wav.scputt2spkspk2utttext相关代码根据文件生成 utt2spk 和 wav.scputt2spk -- spk2utt 转换数据文件准备 在训练/解码中: 有三个文件是必要的: wav.scp 语音编号 – 路径信息utt2spk 语音编号 – 说话人编号spk2utt 说话人编号 …...
91.【SpringBoot-03】
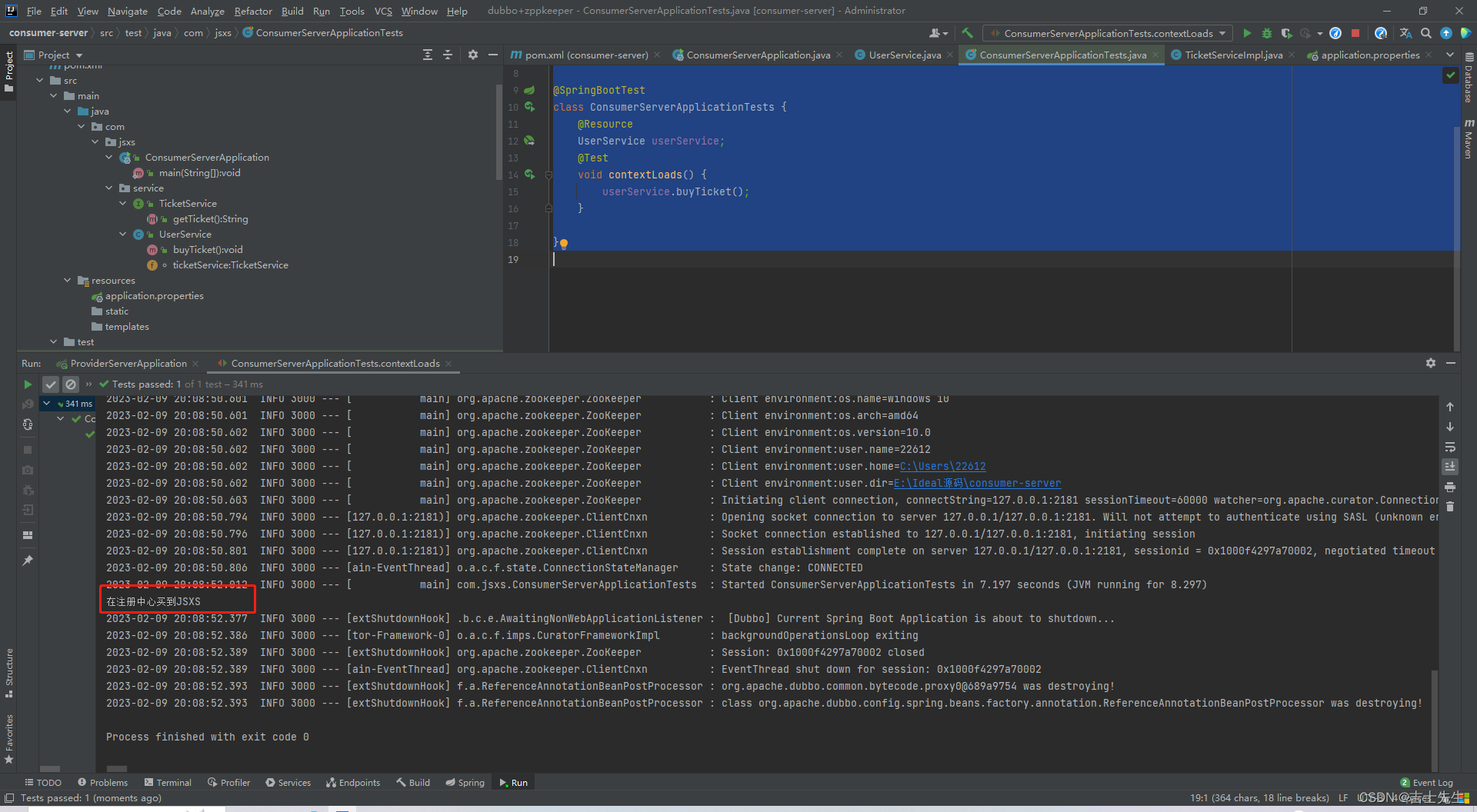
SpringBoot-03(十四)、任务1.异步任务2.邮件任务(1).简单邮箱发送(2).复杂邮箱发送3.定时任务(1).cron表达式(2).特殊表达式(3).定时任务测试(4).常用cron表达式(十五)、Dubbo和Zookeeper集成1.分布式原理(1).Dubbo文档2.什么是RPC?3.Dubbo的概念和介绍(1).Dubbo是什么(2). Du…...
【本地项目】上传到【GitLab】流程详解
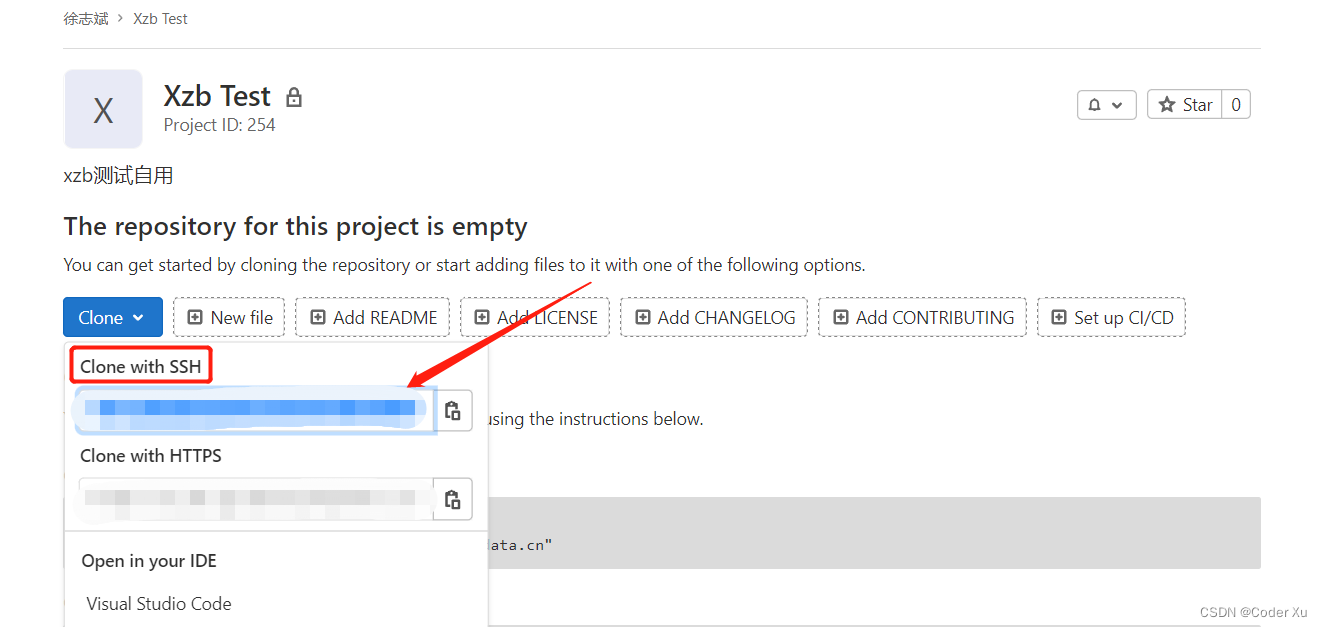
文章目录1、安装Git2、创建GitLab项目文件夹3、创建密钥4、向GitLab上传项目注意:本篇文章中提到的上传流程所需要的命令,几乎在GitLab的Command line instructions中都有所记载 1、安装Git 具体安装流程这里不做过多说明,安装流程可以参考…...

初阶指针C
🚀🚀🚀大家觉不错的话,就恳求大家点点关注,点点小爱心,指点指点🚀🚀🚀 目录 🐰指针是什么 🐰指针和指针类型 🌸指针-整数 &#x…...
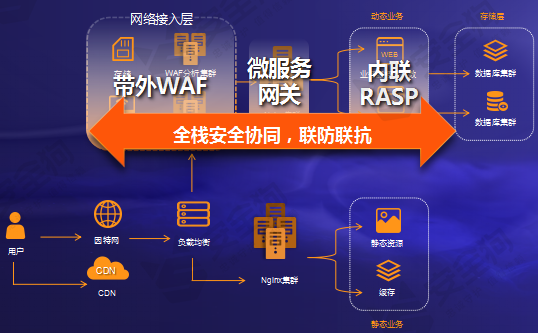
云原生安全2.X 进化论系列|揭秘云原生安全2.X的五大特征
随着云计算技术的蓬勃发展,传统上云实践中的应用升级缓慢、架构臃肿、无法快速迭代等“痛点”日益明显。能够有效解决这些“痛点”的云原生技术正蓬勃发展,成为赋能业务创新的重要推动力,并已经应用到企业核心业务。然而,云原生技…...
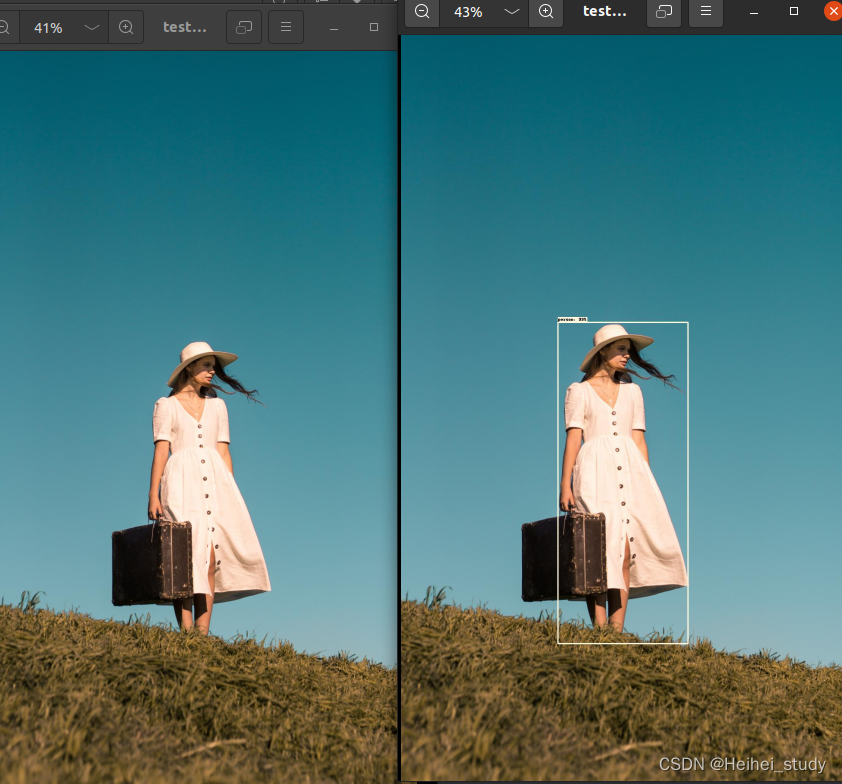
json文件在faster_rcnn中从测试到训练 可行性
1.确认任务 经过mydataset文件处理后 - > 在train_res50_fpn文件内应用 # load train data set # VOCdevkit -> VOC2012 -> ImageSets -> Main -> train.txt train_dataset VOCDataSet(VOC_root, "2012", data_transform["train"], &…...

golang 1.20正式发布,更好更易更强
预期中的Go 2不会有了,1.20也算是一个小gap,从中可以一窥Go未来的发展之路。对于Go来说,未来保持1.x持续演进和兼容性之外,重点就是让Go性能更优,同时保持大道至简原则,使用尽可能容易,从这两个…...

图片显示一半怎么回事?
不知道小伙伴是否遇到过,刚刚上传的一个文件夹,有一多半的图片突然就变成了无法显示该图片或者是图片显示一半,而另外一半就显示灰色蓝色粉色条状。而且还把原文件删除了。面对这种情况,有什么解决方法呢?下面让我们一起来来看看…...
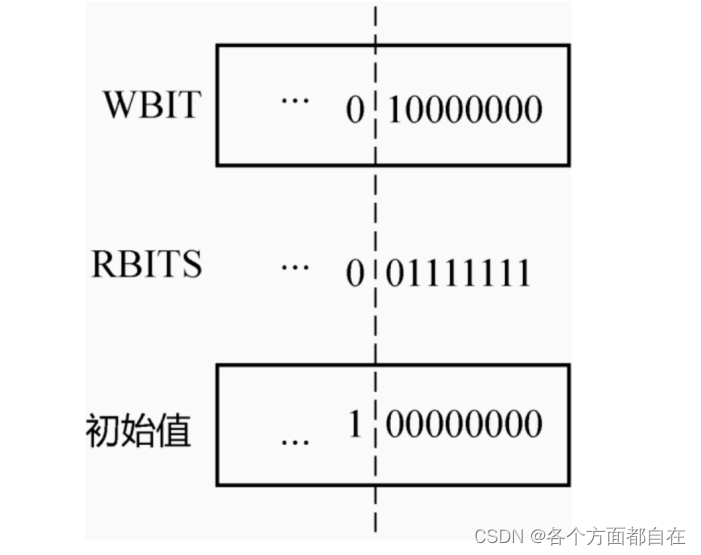
102-并发编程详解(中篇)
这里续写上一章博客 Phaser新特性 : 特性1:动态调整线程个数 CyclicBarrier 所要同步的线程个数是在构造方法中指定的,之后不能更改,而 Phaser 可以在运行期间动态地 调整要同步的线程个数,Phaser 提供了下面这些方…...
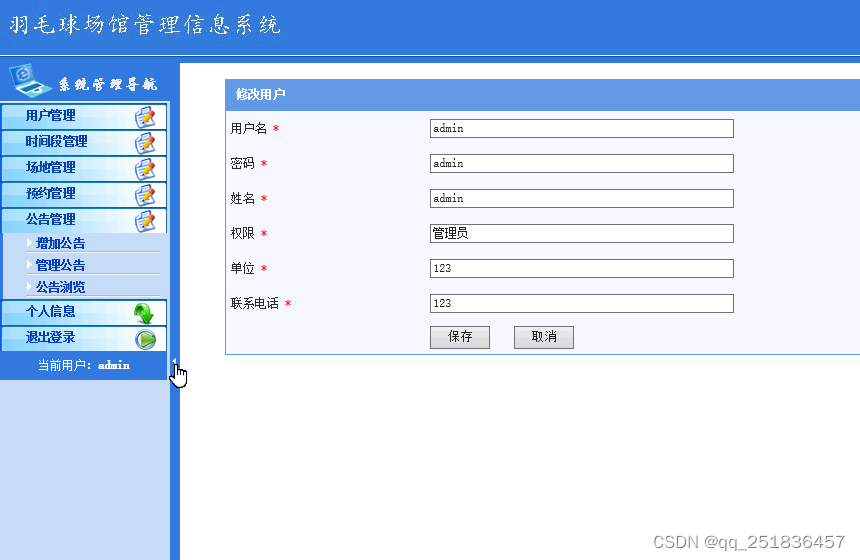
jsp羽毛球场馆管理系统Myeclipse开发mysql数据库web结构java编程计算机网页项目
一、源码特点 jsp 羽毛球场馆管理系统 是一套完善的web设计系统,对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为 TOMCAT7.0,Myeclipse8.5开发,数据库为Mysql,…...
CacheLib 原理说明
CacheLib 介绍 CacheLib 是 facebook 开源的一个用于访问和管理缓存数据的 C 库。它是一个线程安全的 API,使开发人员能够构建和自定义可扩展的并发缓存。 主要功能: 实现了针对 DRAM 和 NVM 的混合缓存,可以将从 DRAM 驱逐的缓存数据持久…...
【dapr】服务调用(Service Invokation) - app id的解析
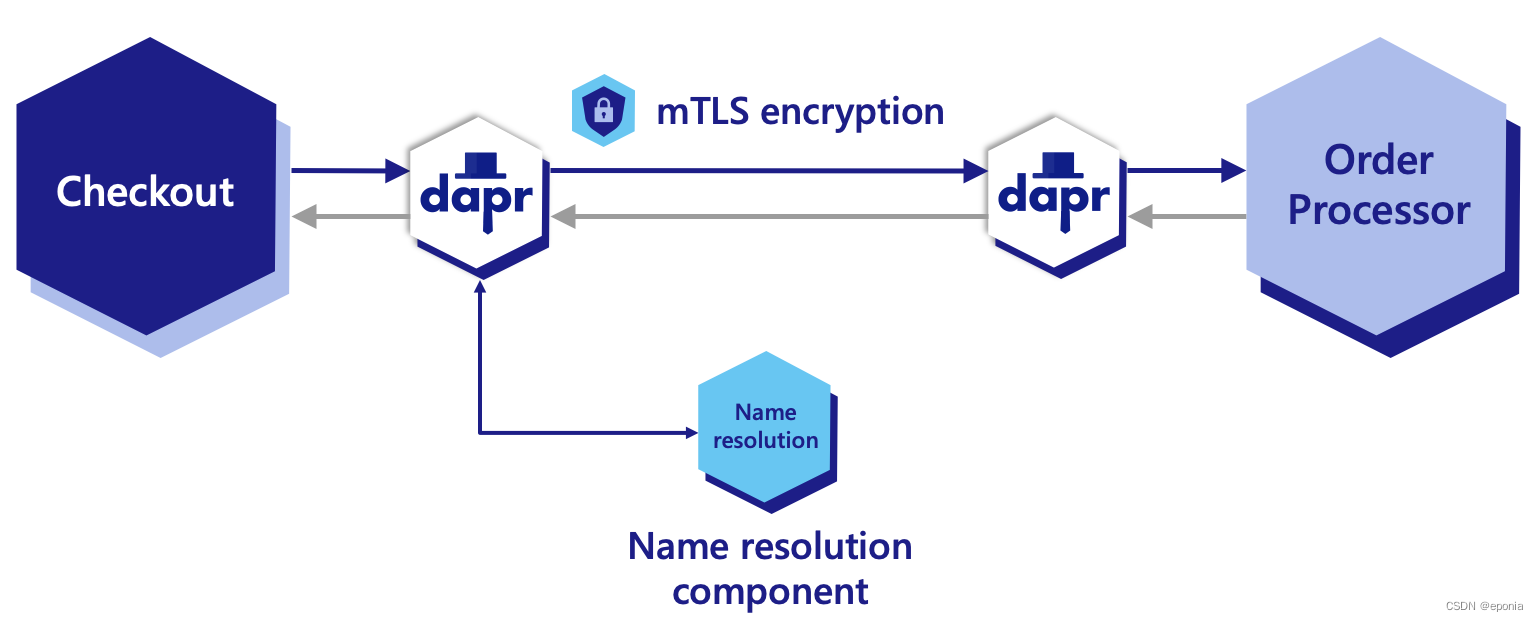
逻辑图解 上图来自Dapr官网教程,其中Checkout是一个服务,负责生成订单号, Order Processor是另一个服务,负责处理订单。Checkout服务需要调用Order Processor的API, 让Order Processor获取到其生成的订单号并进行处理。…...
Odoo丨5步轻松实现在Odoo中打开企微会话框
Odoo丨5步轻松实现在Odoo中打开企微会话框 在Odoo中开启企微会话框 企业微信作为一个很好的企业级应用发布平台,尤其是提供的数据和接口,极大地为很多企业级应用提供便利,在日常中应用广泛! 最近在项目中就遇到一个与企业微信相…...
python读取.stl文件
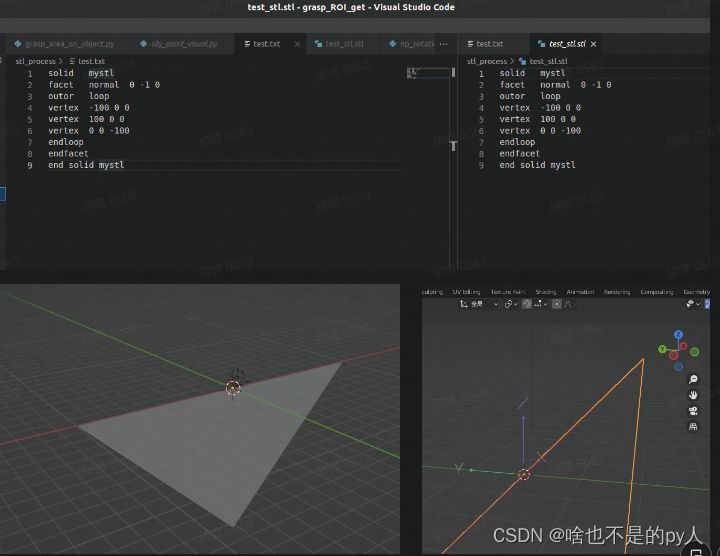
目录 .1 文本方式读取 1.2 stl解析 1.3 stl创建 .2 把点转换为.stl .1 文本方式读取 代码如下 stl_path/home/pxing/codes/point_improve/data/003_cracker_box/0.stlpoints[] f open(stl_path) lines f.readlines() prefixvertex num3 for line in lines:#print (l…...
vue2.0项目第一部分
论坛项目后端管理系统服务器地址:http://172.16.11.18:9090swagger地址:http://172.16.11.18:9090/doc.html前端h5地址:http://172.16.11.18:9099/h5/#/前端管理系统地址:http://172.16.11.18:9099/admin/#/搭建项目vue create . …...
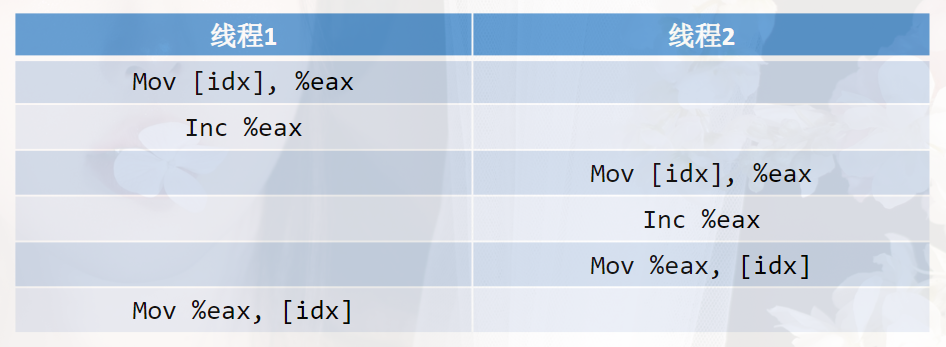
锁与原子操作
锁与原子操作 锁 以自增操作为例子: void *func(void *arg) {int *pcount (int *)arg;int i 0;//while (i < 100000) {(*pcount) ; // 并不会到达100000usleep(1);} }int main(){int i 0;for (i 0;i < THREAD_COUNT;i ) {pthread_create(&thid…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...

GAN模式奔溃的探讨论文综述(一)
简介 简介:今天带来一篇关于GAN的,对于模式奔溃的一个探讨的一个问题,帮助大家更好的解决训练中遇到的一个难题。 论文题目:An in-depth review and analysis of mode collapse in GAN 期刊:Machine Learning 链接:...
