基础算法——搜索与图论
搜索与图论
- 图的存储方式
- 2、最短路问题
- 2.1、Dijkstra算法(朴素版)
- 2.2、Dijkstra算法(堆优化版)
- 2.3、Bellman-Ford算法
- 2.4、SPFA求最短路
- 2.5、SPFA判负环
- 2.6、Floyd算法
图的存储方式

2、最短路问题
最短路问题可以分为单源最短路问题和多源最短路问题,单源最短路问题就是求出从点1->n的最短距离,而多源最短路问题就是求出从点i->j的最短距离。单源最短路问题还可以分为正权边的单源最短路问题和负权边的单源最短路问题。具体算法和时间复杂度如下图:
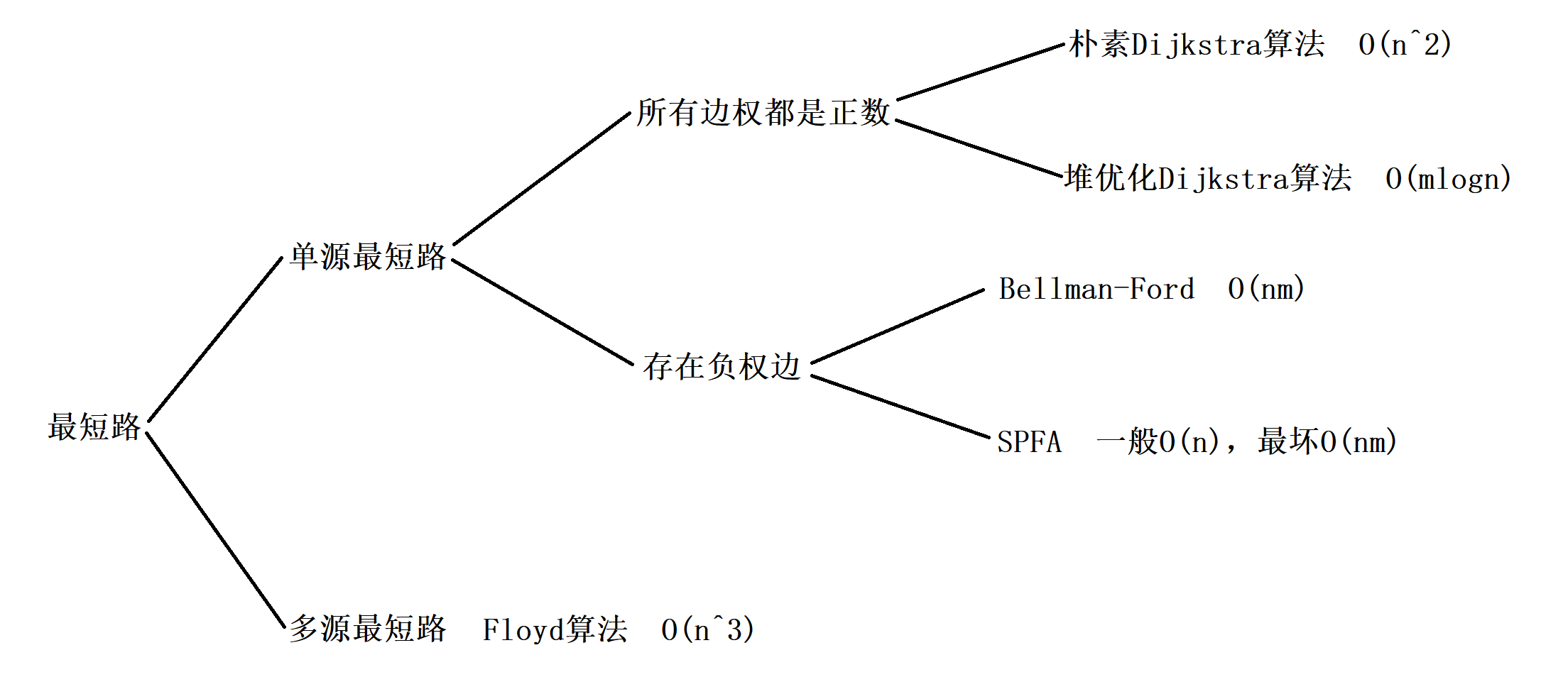
2.1、Dijkstra算法(朴素版)

算法模板:
#include <iostream>
#include <cstring>using namespace std;
const int N = 510;
int g[N][N], d[N];
int n, m;
bool st[N];int dijkstra()
{memset(d, 0x3f, sizeof d);d[1] = 0;for (int i = 0; i < n; i++){int t = -1;for (int j = 1; j <= n; j++)if (!st[j] && (t == -1 || d[t] > d[j]))t = j;st[t] = true;for (int j = 1; j <= n; j++)d[j] = min(d[j], d[t] + g[t][j]);}return d[n] == 0x3f3f3f3f ? -1 : d[n];
}int main()
{cin >> n >> m;memset(g, 0x3f, sizeof g);while (m--){int a, b, c;scanf("%d%d%d", &a, &b, &c);g[a][b] = min(g[a][b], c);}cout << dijkstra() << endl;return 0;
}
2.2、Dijkstra算法(堆优化版)
下面来看看如何优化:

算法模板:
#include <iostream>
#include <cstring>
#include <queue>using namespace std;
typedef pair<int, int> PII;
const int N = 1.5e5+10;
int h[N], e[N], w[N], ne[N], idx;
int n, m, d[N];
bool st[N];void add(int a, int b, int c)
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}int dijkstra()
{memset(d, 0x3f, sizeof d);d[1] = 0;priority_queue<PII, vector<PII>, greater<PII>> heap;heap.push({0, 1});while (heap.size()){auto t = heap.top();heap.pop();int ver = t.second, dis = t.first;if (st[ver]) continue;st[ver] = true;for (int i = h[ver]; i != -1; i = ne[i]){int j = e[i];if (d[j] > dis + w[i]){d[j] = dis + w[i];heap.push({d[j], j});}}}return d[n] == 0x3f3f3f3f ? -1 : d[n];
}int main()
{cin >> n >> m;memset(h, -1, sizeof h);while (m--){int a, b, c;scanf("%d%d%d", &a, &b, &c);add(a, b, c);}cout << dijkstra() << endl;return 0;
}
2.3、Bellman-Ford算法

代码模板:
#include <iostream>
#include <cstring>using namespace std;
const int N = 510, M = 10010;
int n, m, k;
int d[N], backup[N];struct Edge
{int a, b, w;
}edges[M];void bellman_ford()
{memset(d, 0x3f, sizeof d);d[1] = 0;for (int i = 0; i < k; i++){memcpy(backup, d, sizeof d);for (int j = 0; j < m; j++){auto e = edges[j];d[e.b] = min(d[e.b], backup[e.a] + e.w);}}
}int main()
{cin >> n >> m >> k;for (int i = 0; i < m; i++){int a, b, w;scanf("%d%d%d", &a, &b, &w);edges[i] = {a, b, w};}bellman_ford();if (d[n] > 0x3f3f3f3f / 2) cout << "impossible" << endl;else cout << d[n] << endl;return 0;
}
2.4、SPFA求最短路

代码模板:
#include <iostream>
#include <cstring>
#include <queue>using namespace std;
const int N = 1e5+10;
int n, m;
int h[N], e[N], w[N], ne[N], idx;
int d[N];
bool st[N];void add(int a, int b, int c)
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}void spfa()
{memset(d, 0x3f, sizeof d);d[1] = 0;queue<int> q;q.push(1);st[1] = true;while (q.size()){auto t = q.front();q.pop();st[t] = false;for (int i = h[t]; i != -1; i = ne[i]){int j = e[i];if (d[j] > d[t] + w[i]){d[j] = d[t] + w[i];if (!st[j]){st[j] = true;q.push(j);}}}}
}int main()
{cin >> n >> m;memset(h, -1, sizeof h);while (m--){int a, b, c;scanf("%d%d%d", &a, &b, &c);add(a, b, c);}spfa();if (d[n] == 0x3f3f3f3f) cout << "impossible" << endl;else cout << d[n] << endl;return 0;
}
2.5、SPFA判负环

#include <iostream>
#include <cstring>
#include <queue>using namespace std;
const int N = 2010, M = 10010;
int h[N], e[M], w[M], ne[M], idx;
int n, m;
int d[N], cnt[N];
bool st[N];void add(int a, int b, int c)
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}bool spfa()
{queue<int> q;for (int i = 1; i <= n; i++){q.push(i);st[i] = true;}while (q.size()){auto t = q.front();q.pop();st[t] = false;for (int i = h[t]; i != -1; i = ne[i]){int j = e[i];if (d[j] > d[t] + w[i]){d[j] = d[t] + w[i];cnt[j] = cnt[t] + 1;if (cnt[j] >= n) return true;if (!st[j]){st[j] = true;q.push(j);}}}}return false;
}int main()
{cin >> n >> m;memset(h, -1, sizeof h);while (m--){int a, b, c;scanf("%d%d%d", &a, &b, &c);add(a, b, c);}if (spfa()) cout << "Yes" << endl;else cout << "No" << endl;return 0;
}
2.6、Floyd算法

#include <iostream>
#include <cstring>using namespace std;
const int N = 210, INF = 0x3f3f3f3f;
int d[N][N];
int n, m, k;void floyd()
{for (int k = 1; k <= n; k++)for (int i = 1; i <= n; i++)for (int j = 1; j <= n; j++)d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}int main()
{cin >> n >> m >> k;for (int i = 1; i <= n; i++)for (int j = 1; j <= n; j++)if (i == j) d[i][j] = 0;else d[i][j] = INF;while (m--){int a, b, c;cin >> a >> b >> c;d[a][b] = min(d[a][b], c);}floyd();while (k--){int l, r;cin >> l >> r;if (d[l][r] > INF / 2) cout << "impossible" << endl;else cout << d[l][r] << endl;}return 0;
}
相关文章:

基础算法——搜索与图论
搜索与图论 图的存储方式2、最短路问题2.1、Dijkstra算法(朴素版)2.2、Dijkstra算法(堆优化版)2.3、Bellman-Ford算法2.4、SPFA求最短路2.5、SPFA判负环2.6、Floyd算法 图的存储方式 2、最短路问题 最短路问题可以分为单源最短路…...
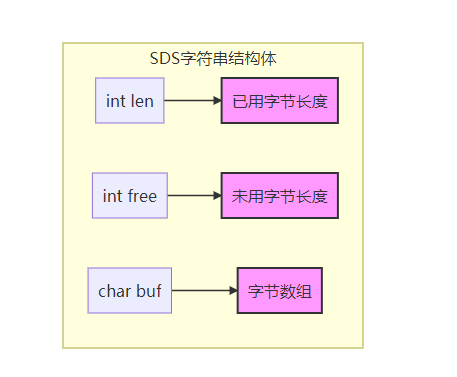
redis优化编码之字符串
redis 优化编码之字符串 ### 字符串优化 字符串对象是redis内部最常用的数据类型。 所有的键是字符串对象值对象除了整数之外都是使用字符串存储lpush cache:type "redis" "tair" "memcache" "leveldb"创建如上一个链表 需要创建一…...
Python特定版本的安装/卸载/环境配置,Spyder安装教程
目录 1.Python安装 1.1 Python下载 1.2 下载特定版本 1.3 安装Python 1.4 修改安装 1.5 环境配置 1.6 卸载Python 2.Spyder安装使用 2.1 Spyder下载 2.1.1 官网下载Spyder 2.2.2 Github下载Spyder 2.2 安装 参考资料:网盘 1.Python安装 1.1 Python下载…...
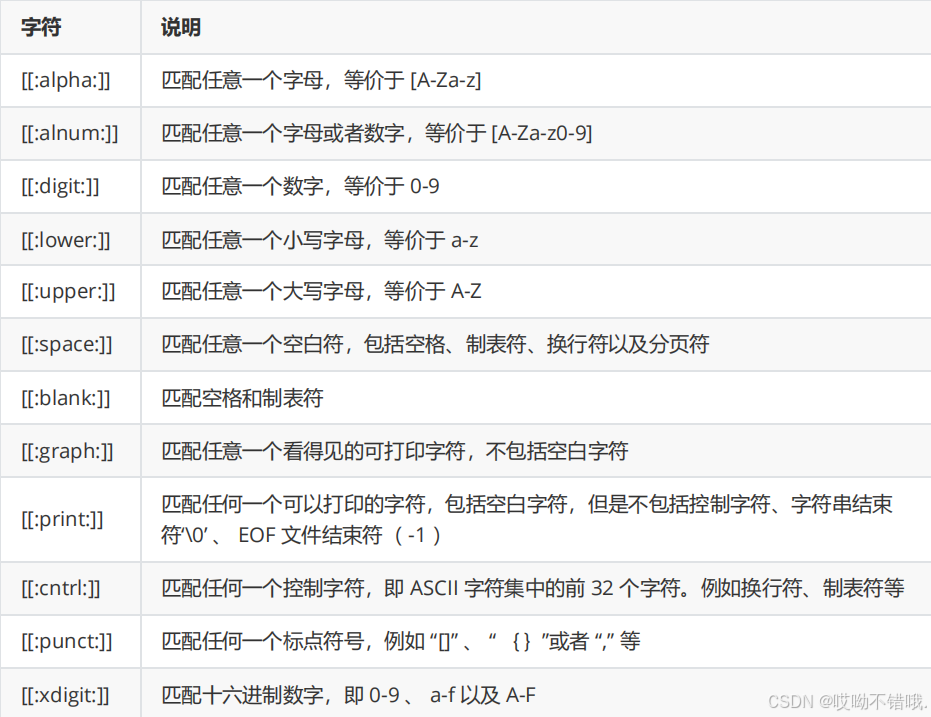
全局搜索正则表达式(grep)
一.grep简介 grep 全程Globally search a Regular Expression and Print,是一种强大的文本搜索工具,它能使用特定模式匹配(包括正则表达式)搜索文本,并默认输出匹配行。Unix的grep家族包括grep和egrep 二.grep的工作…...

linux-12 关于shell(十一)ls
登录系统输入用户名和密码以后,会显示给我们一个命令提示符,就意味着我们在这里就可以输入命令了,给一个命令,这个命令必须要可执行,那问题是我的命令怎么去使用,命令格式有印象吗?在命令提示符…...

编写指针函数使向右循环移动m个位置
题目描述:有n个整数,要求你编写一个函数使其向右循环移动m个位置 请仔细阅读右侧代码,结合相关知识,在Begin-End区域内进行代码补充。 输入 输入n m表示有n个整数,移动m位 输出 输出移动后的数组 样例输入: 10 5 1 2 3…...

xvisor调试记录
Xvisor是一种开源hypervisor,旨在提供完整、轻量、移植且灵活的虚拟化解决方案,属于type-1类型的虚拟机,可以直接在裸机上启动。 启动xvisor步骤: 1、搭建riscv编译环境 首先从github上下载riscv-gnu-toolchain很费劲,建议直接从国内的源下载 git clone https://gitee…...

MongoDB-ObjectID 生成器
前言 MongoDB中一个非常关键的概念就是 ObjectID,它是 MongoDB 中每个文档的默认唯一标识符。了解 ObjectID 的生成机制不仅有助于开发人员优化数据库性能,还能帮助更好地理解 MongoDB 的设计理念。 什么是 MongoDB ObjectID? 在 MongoDB …...
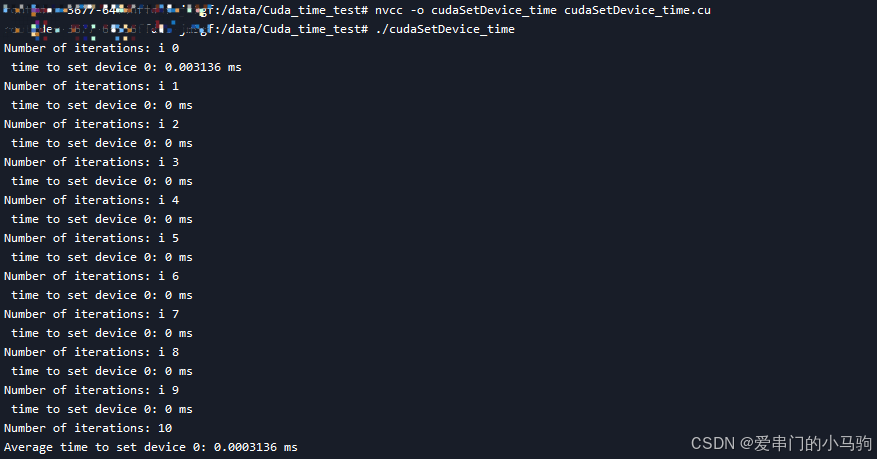
CUDA 计时功能,记录GPU程序/函数耗时,cudaEventCreate,cudaEventRecord,cudaEventElapsedTime
为了测试GPU函数的耗时,可以使用 CUDA 提供的计时功能:cudaEventCreate, cudaEventRecord, 和 cudaEventElapsedTime。这些函数可以帮助你测量某个 CUDA 操作(如设置设备)所花费的时间。 一、记录耗时案例 以下是一个示例程序&a…...
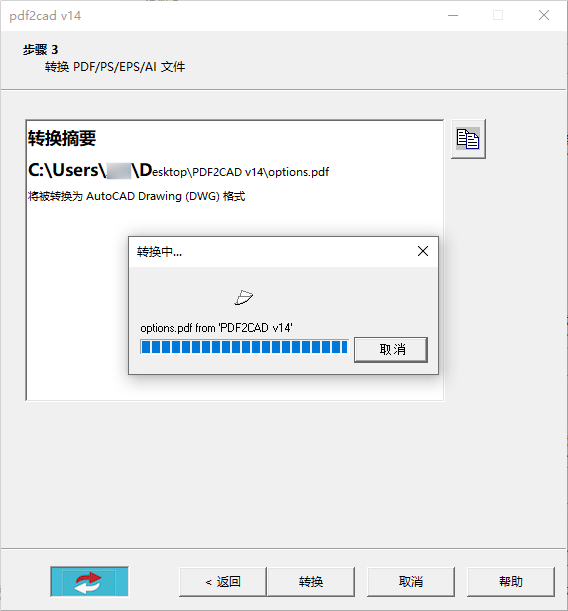
PDF 文件如何转为 CAD 图纸?PDF2CAD 使用教程
在工程设计和建筑行业中,PDF 文件常常被用来分享和存档图纸。然而,当需要对这些图纸进行编辑或进一步开发时,静态的 PDF 格式就显得力不从心了。这时候,将 PDF 文件转换为可编辑的 CAD(计算机辅助设计)格式…...
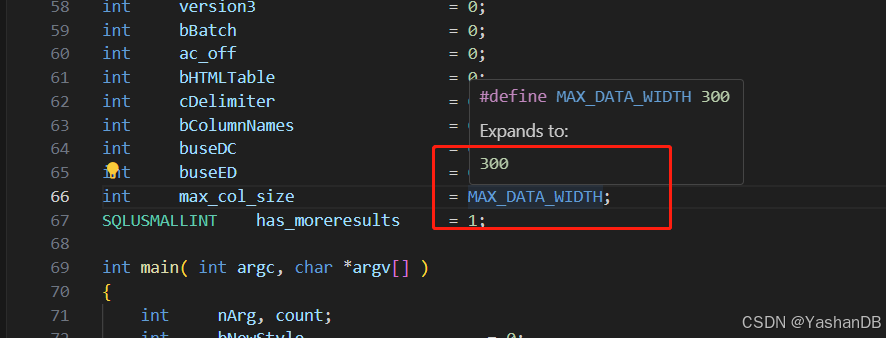
【YashanDB知识库】php查询超过256长度字符串,数据被截断的问题
本文内容来自YashanDB官网,原文内容请见:https://www.yashandb.com/newsinfo/7488290.html?templateId1718516 问题现象 如下图,php使用odbc数据源,查询表数据,mysql可以显示出来,yashan显示数据被截断。…...

暴雨AI加速计算服务器新品X8840上市
用户输入简短的文字,大模型可以自动生成创意文本或图像;金融机构的风险评估和预测,大模型通过对金融数据的分析,可以识别异常交易行为;15秒内完成中英文作文的批改和评分,并提供针对性的改进建议࿰…...
共享目录的步骤如下:)
在多个分布式机器间设置和使用 NFS(Network File System)共享目录的步骤如下:
在多个分布式机器间设置和使用 NFS(Network File System)共享目录的步骤如下: 1. 准备工作 确保所有参与的机器都在同一个网络中,并安装了 NFS 软件包。 在 Linux 系统上: sudo apt update && sudo apt install nfs-kernel-server -y # Ubuntu/Debian sudo yu…...
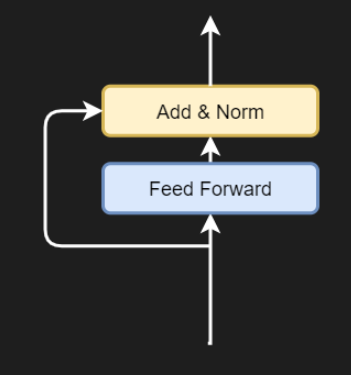
机器学习中的 Transformer 简介(第 1 部分)
目录 一、说明 二、为什么是 Transformer? 三、什么是 Transformer? 3.1 译者的类比 四、编码器部分 4.1 、从文本输入到输入嵌入 4.2 词嵌入 4.2 N倍编码器段 4.4 多头注意力机制 4.5 添加残差和层归一化 4.6 添加残差和层归一化 五、总结 一、说明 西如…...

D3实现站点路线图demo分享
分享一下通过D3实现的站点路线分布图,这是一个demo。效果图如下: 源码如下: <template><div class"map-test" ref"d3Chart"><div class"tooltip" id"popup-element"><span>…...

非文件形式的内存动态函数库调用接口
使用memfd的系统调用接口将动态库加载到proc虚拟文件系统,提供的fd为进程持有的句柄,通过dlopen的path指向此句柄,即可实现非文件系统加载动态链接库。 文章目录 一、memfd_create二、dl_open三、示例参考 一、memfd_create 接口名称int mem…...
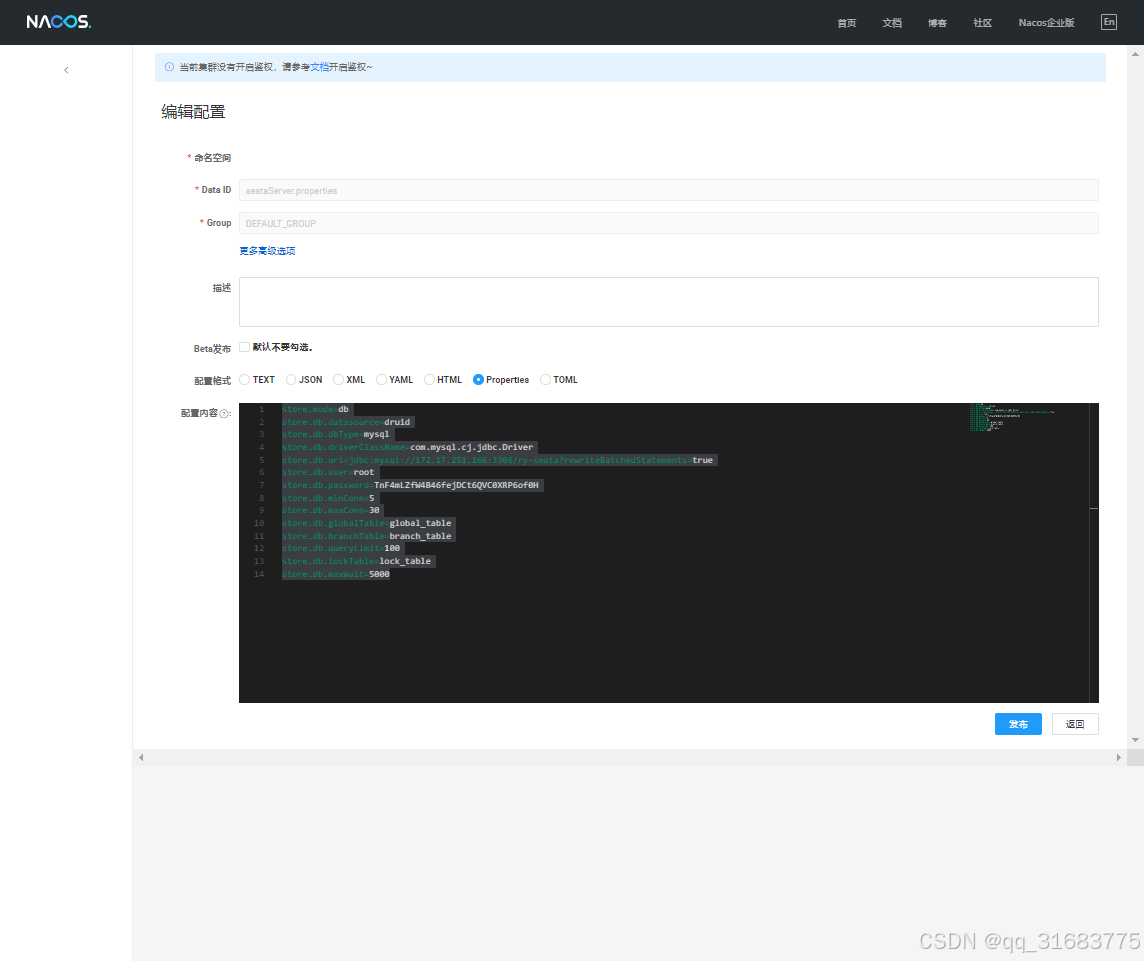
liunx docker 部署 nacos seata sentinel
部署nacos 1.按要求创建好数据库 2.创建docker 容器 docker run -d --name nacos-server -p 8848:8848 -p 9848:9848 -p 9849:9849 -e MODEstandalone -e SPRING_DATASOURCE_PLATFORMmysql -e MYSQL_SERVICE_HOST172.17.251.166 -e MYSQL_SERVICE_DB_NAMEry-config -e MYSQL…...
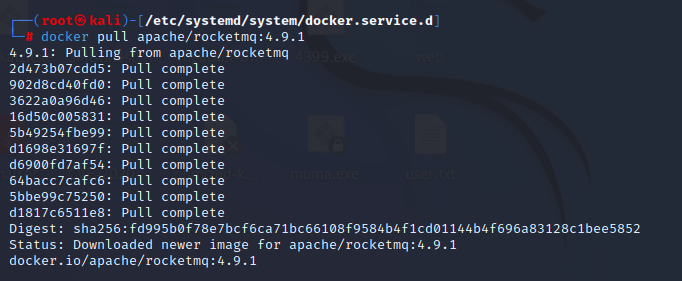
解决没法docker pull问题
没想到国内源死差不多了,以下内容需要提前科学上网 su cd /etc/systemd/system/docker.service.d vim proxy.conf 参照下图修改,代理服务器改成你自己的。 [Service] Environment"HTTP_PROXYsocks5://192.168.176.180:10810" Environment&…...

面试小札:闪电五连鞭_2
1 请简单描述一下Java中的多线程。 多线程是指在一个程序中可以同时运行多个线程来执行不同的任务。在Java中,通过 java.lang.Thread 类来创建和控制线程。可以通过继承 Thread 类或者实现 Runnable 接口的方式来定义线程的执行逻辑。 线程有多种状态,…...

Milvus向量数据库06-RAG检索增强
Milvus向量数据库06-RAG检索增强 文章目录 Milvus向量数据库06-RAG检索增强1-学习目标2-参考网址3-执行过程记录1-到底什么是RAGRAG 的基本流程:为什么 RAG 优于传统的基于检索的方法:示例流程: 2-RAG和Elasticsearch对比3-RAG和向量数据库之…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...
