【C++】等差数列末项计算题解析及优化

文章目录
- 💯前言
- 💯题目描述与输入输出要求
- 💯数学分析与公式推导
- 公差的计算
- 通项公式推导
- 💯示例解析
- 解题步骤
- 💯程序实现与解析
- 初版代码
- 代码解析
- 优点与不足
- 改进实现:显式处理特殊情况
- 改进点分析
- 优点与不足
- 💯代码优化与封装
- 封装代码
- 优化点说明
- 💯实用提示与总结
- 💯小结

💯前言
- 等差数列是数学领域中极为重要的一类数列,其核心特征是任意相邻两项的差值保持不变。这一特性使得等差数列在
代数与数论研究中扮演着重要角色,同时广泛应用于数据建模、工程预测以及数值分析等实际场景。
本题的目标是,在给定等差数列的前两项 a 1 , a 2 a_1, a_2 a1,a2 的基础上,计算该数列的第 n n n 项。这一问题旨在测试解题者对等差数列公式的掌握、算法设计能力以及程序实现的准确性。
C++ 参考手册

💯题目描述与输入输出要求
![]()
题目描述
本题要求计算等差数列的第 n n n 项值。等差数列的定义如下:
- 任意相邻两项之间的差值为一个常量,称为公差 d d d。
- 数列的通项公式表达为:
a n = a 1 + ( n − 1 ) ⋅ d a_n = a_1 + (n - 1) \cdot d an=a1+(n−1)⋅d
其中:- a n a_n an 表示数列的第 n n n 项。
- a 1 a_1 a1 表示数列的第一项。
- d d d 表示数列的公差。
输入格式
输入为一行,包含三个整数 a 1 , a 2 , n a_1, a_2, n a1,a2,n,满足以下条件:
- − 100 ≤ a 1 , a 2 ≤ 100 -100 \leq a_1, a_2 \leq 100 −100≤a1,a2≤100
- 0 < n ≤ 1000 0 < n \leq 1000 0<n≤1000
输出格式
程序输出一个整数,即数列的第 n n n 项的值。
输入输出示例
示例 1
输入:
1 4 100
输出:
298
💯数学分析与公式推导
![]()
公差的计算
![]()
公差 d d d 是等差数列的核心特性,由定义可得:
d = a 2 − a 1 d = a_2 - a_1 d=a2−a1
一旦确定了公差,便可以通过递推或通项公式计算出数列中的任意一项。
通项公式推导
![]()
将公差公式代入通项公式,我们得到:
a n = a 1 + ( n − 1 ) ⋅ ( a 2 − a 1 ) a_n = a_1 + (n - 1) \cdot (a_2 - a_1) an=a1+(n−1)⋅(a2−a1)
或者,从第二项 a 2 a_2 a2 出发,公式可以等价写为:
a n = a 2 + ( n − 2 ) ⋅ ( a 2 − a 1 ) a_n = a_2 + (n - 2) \cdot (a_2 - a_1) an=a2+(n−2)⋅(a2−a1)
这一形式为代码实现提供了更为灵活的选择。
💯示例解析
![]()
输入示例
1 4 100
解题步骤
![]()
-
计算公差 d d d:
d = a 2 − a 1 = 4 − 1 = 3 d = a_2 - a_1 = 4 - 1 = 3 d=a2−a1=4−1=3 -
计算第 100 项 a 100 a_{100} a100:
a 100 = a 1 + ( 100 − 1 ) ⋅ d = 1 + 99 ⋅ 3 = 1 + 297 = 298 a_{100} = a_1 + (100 - 1) \cdot d = 1 + 99 \cdot 3 = 1 + 297 = 298 a100=a1+(100−1)⋅d=1+99⋅3=1+297=298 -
验证结果:
- 通过代入公式验证,计算结果符合逻辑且准确。
输出结果
298
💯程序实现与解析
![]()
初版代码
以下代码直接采用公式实现:
#include <iostream>
using namespace std;int main() {int a1, a2, n;cin >> a1 >> a2 >> n;cout << (a2 - a1) * (n - 2) + a2 << endl;return 0;
}

代码解析
![]()
-
输入部分:
- 从标准输入读取 a 1 , a 2 , n a_1, a_2, n a1,a2,n。
-
计算部分:
- 直接使用公式 ( a 2 − a 1 ) ⋅ ( n − 2 ) + a 2 (a_2 - a_1) \cdot (n - 2) + a_2 (a2−a1)⋅(n−2)+a2。该公式等价于:
a n = a 2 + ( n − 2 ) ⋅ ( a 2 − a 1 ) a_n = a_2 + (n - 2) \cdot (a_2 - a_1) an=a2+(n−2)⋅(a2−a1)
- 直接使用公式 ( a 2 − a 1 ) ⋅ ( n − 2 ) + a 2 (a_2 - a_1) \cdot (n - 2) + a_2 (a2−a1)⋅(n−2)+a2。该公式等价于:
-
输出部分:
- 输出计算结果。
优点与不足
![]()
- 优点:
- 简洁直接,适合处理一般情况。
- 不足:
- 未显式处理特殊情况(如 n = = 1 n == 1 n==1 和 n = = 2 n == 2 n==2),可能导致逻辑混乱。
- 对初学者而言,公式的隐式逻辑不够直观。
改进实现:显式处理特殊情况
以下代码改进了特殊情况的处理:
#include <iostream>
using namespace std;int main() {int a1, a2, n;cin >> a1 >> a2 >> n;if (n == 1)cout << a1 << endl;else if (n == 2)cout << a2 << endl;elsecout << a2 + (n - 2) * (a2 - a1) << endl;return 0;
}

改进点分析
![]()
-
特殊情况处理:
- n = = 1 n == 1 n==1 时输出 a 1 a_1 a1。
- n = = 2 n == 2 n==2 时输出 a 2 a_2 a2。
-
一般情况处理:
- 使用通项公式计算第 n n n 项。
优点与不足
![]()
- 优点:
- 逻辑更加清晰,适合扩展和调试。
- 不足:
- 存在一定的重复代码。
💯代码优化与封装
![]()
为进一步提升代码的复用性与可维护性,我们可以将核心逻辑封装为函数:
封装代码
#include <iostream>
using namespace std;// 计算等差数列的第 n 项
int calculateTerm(int a1, int a2, int n) {if (n == 1)return a1;else if (n == 2)return a2;elsereturn a2 + (n - 2) * (a2 - a1);
}int main() {int a1, a2, n;cin >> a1 >> a2 >> n;cout << calculateTerm(a1, a2, n) << endl;return 0;
}

优化点说明
![]()
-
逻辑模块化:
- 核心逻辑被独立为
calculateTerm函数,使主程序简洁明了。
- 核心逻辑被独立为
-
增强可读性:
- 函数命名直观,便于理解其功能。
-
便于扩展:
- 若需增加输入验证或边界处理,可直接在函数中实现。
💯实用提示与总结
![]()
提示 1:边界条件的重要性
- 在实现时,应显式处理边界情况(如 n = = 1 n == 1 n==1 和 n = = 2 n == 2 n==2)。
- 对异常输入(如 n ≤ 0 n \leq 0 n≤0)进行适当的错误提示。
提示 2:公式的灵活应用
- 根据不同场景,选择从 a 1 a_1 a1 或 a 2 a_2 a2 出发的通项公式,可以优化计算。
提示 3:逐步验证结果
- 对公式的每一步代入进行验证,确保逻辑严谨。
提示 4:代码调试策略
- 利用断点调试工具,逐步检查变量值与计算结果。
💯小结

通过本文的分析与优化,我们明确了以下要点:
- 公式掌握是解题核心:
- 等差数列的通项公式及其变形是解决此类问题的基础。
- 特殊情况处理提升代码健壮性:
- 显式处理边界条件可以避免潜在逻辑错误。
- 封装与模块化设计增强代码质量:
- 将逻辑独立为函数,提升了代码的可读性、复用性与维护性。

相关文章:

【C++】等差数列末项计算题解析及优化
博客主页: [小ᶻ☡꙳ᵃⁱᵍᶜ꙳] 本文专栏: C 文章目录 💯前言💯题目描述与输入输出要求💯数学分析与公式推导公差的计算通项公式推导 💯示例解析解题步骤 💯程序实现与解析初版代码代码解析优点与不足…...

vue中父组件接收子组件的多个参数的方法:$emit或事件总线
方法一:使用 $emit 方法 原理 子组件通过 $emit 方法向父组件发送事件,同时可以传递多个参数,父组件通过事件监听来接收这些参数。 示例 子组件代码 <template><div><button click"sendData">发送数据</…...

2024.12.10——攻防世界Web_php_include
知识点:代码审计 文件包含 伪协议 伪协议知识点补充: 在PHP中,伪协议(Pseudo Protocols)也被称为流包装器,这些伪协议以 php://开头,后面跟着一些参数,用于指定要执行的操作或需要…...
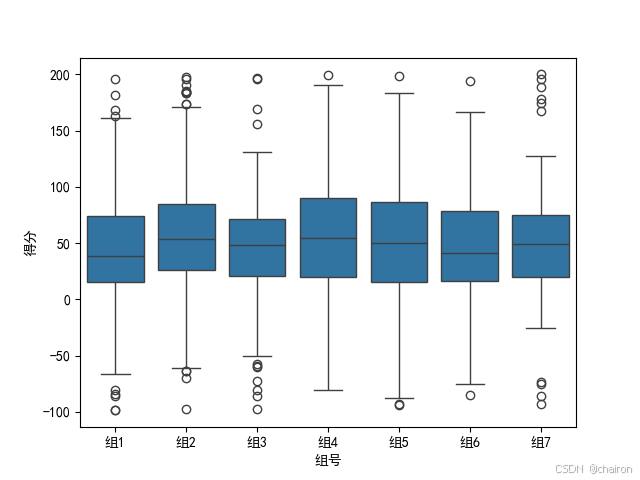
【机器学习算法】——数据可视化
1. 饼图:显示基本比例关系 import matplotlib.pyplot as pltplt.rcParams[font.sans-serif] [SimHei] plt.rcParams[axes.unicode_minus] False# ——————————————————————————————————————————————————————…...

如何在 Android 项目中实现跨库传值
背景介绍 在一个复杂的 Android 项目中,我们通常会有多个库(lib),而主应用程序(app)依赖所有这些库。目前遇到的问题是,在这些库中,libAd 需要获取 libVip 的 VIP 等级状态…...

JavaCV之FFmpegFrameFilter视频转灰度
1、代码 package com.example.demo.ffpemg;import lombok.SneakyThrows; import org.bytedeco.javacv.*;public class FFmpegFrameFilterVideoExample {SneakyThrowspublic static void main(String[] args) {// 输入视频文件路径String inputVideoPath "f:/2222.mp4&qu…...

Redis:基于PubSub(发布/订阅)、Stream流实现消息队列
Redis - PubSub、Stream流 文章目录 Redis - PubSub、Stream流1.基于List的消息队列2.基于PubSub的消息队列3.基于Stream的消息队列1.Redis Streams简介2.Redis Streams基本命令1.XADD 添加消息到末尾2.XLEN 获取消息长度3.XREAD 读取消息 (单消费模式)4…...
)
C#飞行棋(新手简洁版)
我们要在主函数的顶部写一些全局静态字段 确保能在后续的静态方法中能够获取到这些值和修改 static int[] Maps new int[100];static string[] PlayerName new string[2];static int[] PlayerScore new int[2];static bool[] Flags new bool[2] {true,true }; static int[]…...

【OpenCV】图像转换
理论 傅立叶变换用于分析各种滤波器的频率特性。对于图像,使用 2D离散傅里叶变换(DFT) 查找频域。快速算法称为 快速傅立叶变换(FFT) 用于计算DFT。 Numpy中的傅立叶变换 首先,我们将看到如何使用Numpy查…...

力扣 重排链表-143
重排链表-143 /*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next)…...
)
【Kubernetes理论篇】容器集群管理系统Kubernetes(K8S)
Kubernetes集群部署基本管理实战 这么好的机会,还在等什么! 01、Kubernetes 概述 K8S是什么 K8S 的全称为 Kubernetes (K12345678S),PS:“嘛,写全称也太累了吧,写”。不如整个缩写 K8s 作为缩写的结果…...

Kubernetes 常用操作大全:全面掌握 K8s 基础与进阶命令
Kubernetes(简称 K8s)作为一种开源的容器编排工具,已经成为现代分布式系统中的标准。它的强大之处在于能够自动化应用程序的部署、扩展和管理。在使用 Kubernetes 的过程中,熟悉常用操作对于高效地管理集群资源至关重要。本文将详…...

爬虫基础之Web网页基础
网页的组成 网页可以分为三大部分–HTML、CSS 和 JavaScript。如果把网页比作一个人,那么 HTML 相当于骨架、JavaScript 相当于肌肉、CSS 相当于皮肤,这三者结合起来才能形成一个完善的网页。下面我们分别介绍一下这三部分的功能。 HTML HTML(Hypertext…...

k8s, deployment
控制循环(control loop) for {实际状态 : 获取集群中对象X的实际状态(Actual State)期望状态 : 获取集群中对象X的期望状态(Desired State)if 实际状态 期望状态{什么都不做} else {执行编排动作…...

使用ensp搭建OSPF+BGP和静态路由,底层PC使用dhcp,实现PC互通
1.4种方式,实现PC2可以互通底层的所有设备 OSPF:OSPF是一种用于互联网协议网络的链路状态路由协议 BGP:是一种用于互联网上进行路由和可达性信息传递的外部网关协议(EGP) 静态路由: 静态路由是一种路由方…...

TÜLU 3: Pushing Frontiers in Open Language Model Post-Training
基本信息 📝 原文链接: https://arxiv.org/abs/2411.15124👥 作者: Nathan Lambert, Jacob Morrison, Valentina Pyatkin, Shengyi Huang, Hamish Ivison, Faeze Brahman, Lester James V. Miranda, Alisa Liu, Nouha Dziri, Shane Lyu, Yuling Gu, Sau…...

深入解读 MySQL EXPLAIN 与索引优化实践
MySQL 是当今最流行的关系型数据库之一,为了提升查询性能,合理使用 EXPLAIN 工具和优化索引显得尤为重要。本文将结合实际示例,探讨如何利用 EXPLAIN 分析查询执行计划,并分享索引优化的最佳实践。 一、EXPLAIN 工具简介 EXPLAIN …...

Flume——进阶(agent特性+三种结构:串联,多路复用,聚合)
目录 agent特性ChannelSelector描述: SinkProcessor描述: 串联架构结构图解定义与描述配置示例Flume1(监测端node1)Flume3(接收端node3)启动方式 复制和多路复用结构图解定义描述配置示例node1node2node3启…...

ragflow连ollama时出现的Bug
ragflow和ollama连接后,已经添加了两个模型但是ragflow仍然一直warn:Please add both embedding model and LLM in Settings > Model providers firstly.这里可能是我一开始拉取的镜像容器太小,容不下当前添加的模型,导…...

基于centos7.7编译Redis6.0
背景: OS:CentOs 7.7 Redis: 6.0.6 编译构建报错如下: In file included from server.c:30:0: server.h:1044:5: error: expected specifier-qualifier-list before ‘_Atomic’_Atomic unsigned int lruclock; /* Clock for LRU eviction …...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...

ui框架-文件列表展示
ui框架-文件列表展示 介绍 UI框架的文件列表展示组件,可以展示文件夹,支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项,适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...
无头浏览器技术:Python爬虫如何精准模拟搜索点击
1. 无头浏览器技术概述 1.1 什么是无头浏览器? 无头浏览器是一种没有图形用户界面(GUI)的浏览器,它通过程序控制浏览器内核(如Chromium、Firefox)执行页面加载、JavaScript渲染、表单提交等操作。由于不渲…...

基于Java的离散数学题库系统设计与实现:附完整源码与论文
JAVASQL离散数学题库管理系统 一、系统概述 本系统采用Java Swing开发桌面应用,结合SQL Server数据库实现离散数学题库的高效管理。系统支持题型分类(选择题、填空题、判断题等)、难度分级、知识点关联,并提供智能组卷、在线测试…...
