目标跟踪算法:SORT、卡尔曼滤波、匈牙利算法
目录
1 目标检测
2 卡尔曼滤波
3《从放弃到精通!卡尔曼滤波从理论到实践》视频简单学习笔记
3.1 入门
3.2 进阶
3.2.1 状态空间表达式
3.2.2 高斯分布
3.3 放弃
3.4 精通
4 匈牙利算法
5 《【运筹学】-指派问题(匈牙利算法)》视频简单笔记
6 SORT算法的具体流程实现
参考文献:
平时工程中基本上都是用SORT跟踪算法,也知道他的大体原理,这次稍微有点时间,我想再认真了解一下里面的卡尔曼滤波和匈牙利算法的公式推导,虽然我这次看完之后大概率后面很快也还是会忘,但是肯定会加深我的理解。
1 目标检测
目标检测(Object Detection): SORT算法采用“Tracking-by-Detection”策略,即算法的输入数据来源于目标检测器。SORT本身不参与目标检测过程,而是利用目标检测器(如Faster R-CNN、YOLO等)的输出结果,通常是一个矩形(bounding box)来表示目标的位置
2 卡尔曼滤波
由于目标检测得到的bounding box会带有噪声,SORT使用卡尔曼滤波来预测目标的位置和速度信息,从而得到下一帧中目标的运动轨迹。卡尔曼滤波是一种递归滤波器,可以对系统的状态进行最优估计。
卡尔曼滤波可以通过利用数学模型预测的值和测量得到的观测值进行数据融合,找到“最优”的估计值(这里的最优指的是均方差最小)。比方说,我们现在要知道t帧时某一目标准确的bbox(即,计算估计值),记为![]() 。我们已知的是1~t-1帧中目标的bbox。现在我们有两种方法得到t帧的bbox:一是通过数学建模,根据1~t-1的信息来预测出t帧的bbox,记为
。我们已知的是1~t-1帧中目标的bbox。现在我们有两种方法得到t帧的bbox:一是通过数学建模,根据1~t-1的信息来预测出t帧的bbox,记为![]() ;二是通过检测算法,直接测量出t帧的bbox,记为
;二是通过检测算法,直接测量出t帧的bbox,记为![]() 。卡尔曼滤波做的事情就是利用
。卡尔曼滤波做的事情就是利用![]() 和
和![]() 来得到
来得到![]() ,具体分两步实现:预测(predict),即通过数学模型计算出
,具体分两步实现:预测(predict),即通过数学模型计算出![]() ;更新(update),结合测量值
;更新(update),结合测量值![]() 得到当前状态(state)的最优估计值。
得到当前状态(state)的最优估计值。
总之,卡尔曼滤波是一种去噪技术,能够在目标检测的基础上,得到更加准确的bbox。
3《从放弃到精通!卡尔曼滤波从理论到实践》视频简单学习笔记
我看的B站的这个学习视频,下面是我的简单的学习笔记,建议还是直接去看原视频,视频链接如下:
从放弃到精通!卡尔曼滤波从理论到实践~_哔哩哔哩_bilibili
3.1 入门

3.2 进阶
3.2.1 状态空间表达式

3.2.2 高斯分布

正态分布就是正常状态下的概率分布。









3.3 放弃





3.4 精通

4 匈牙利算法
匈牙利算法是一种数据关联(Data Association)算法,其实从本质上讲,跟踪算法要解决的就是数据关联问题。假设有两个集合S和T,集合S中有m个元素,集合T中有n个元素,匈牙利算法要做的是把S中的元素和T中的元素两两匹配(可能匹配不上)。结合跟踪的情景,匈牙利算法的任务就是把t帧的bbox与t-1帧的bbox两两匹配,这样跟踪就完成了。
要想匹配就需要一定的准则,匈牙利算法依据的准则是“损失最小“。损失由损失矩阵的形式来表示,损失矩阵描述了匹配两个集合中某两个元素所要花费的代价。
在SORT算法中,匈牙利算法基于目标检测框(Detections)和预测的目标跟踪框(Tracks,)之间的交并比(Intersection over Union, IoU)来构建相似度矩阵。这个矩阵的每个元素表示一个检测框和一个跟踪框之间的相似度,通常用1减去IoU值来表示匹配的代价或损失,然后利用这个矩阵去寻找匹配代价最小的一组匹配,其实匈牙利算法本身还是用iou进行匹配的,然后本质上其实就是检测框和预测的跟踪框匹配后,保证iou最大,也就是匹配代价最小。
5 《【运筹学】-指派问题(匈牙利算法)》视频简单笔记





6 SORT算法的具体流程实现

参考文献:
从放弃到精通!卡尔曼滤波从理论到实践~_哔哩哔哩_bilibili
匈牙利算法-看这篇绝对就够了!-CSDN博客
匈牙利算法详解-CSDN博客
趣写算法系列之--匈牙利算法_匈牙利算法基本原理-CSDN博客
【运筹学】-指派问题(匈牙利算法)_哔哩哔哩_bilibili
相关文章:

目标跟踪算法:SORT、卡尔曼滤波、匈牙利算法
目录 1 目标检测 2 卡尔曼滤波 3《从放弃到精通!卡尔曼滤波从理论到实践》视频简单学习笔记 3.1 入门 3.2 进阶 3.2.1 状态空间表达式 3.2.2 高斯分布 3.3 放弃 3.4 精通 4 匈牙利算法 5 《【运筹学】-指派问题(匈牙利算法)》视…...

Java版-图论-拓扑排序与有向无环图
拓扑排序 拓扑排序说明 对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边<u,v>∈E(G),则u在线性序列中出现在v之前。通常,这样的线性序列称为满足拓扑次序(Topological Order)的序列…...

GTC2024 回顾 | 优阅达携手 HubSpot 亮相上海,赋能企业数字营销与全球业务增长
从初创企业入门到成长型企业拓展,再到 AI 驱动智能化运营,HubSpot 为企业的每步成长提供了全方位支持。 2024 年 11 月下旬,备受瞩目的 GTC2024 全球流量大会(上海)成功举办。本次大会汇聚了全国内多家跨境出海领域企业…...

eclipse启动的时候,之前一切很正常,但突然报Reason: Failed to determine a suitable driver class的解决
1、之前项目都是启动正常的,然后运行以后发现启动不了了,还会报错: 2、这个Reason: Failed to determine a suitable driver class,说是没有合适的驱动class spring:datasource:url: jdbc:sqlserver://192.168.1.101:1433;databa…...

_tkinter.TclError: can‘t find package tkdnd Unable to load tkdnd library.解决办法
Traceback (most recent call last): File “tkinterdnd2\TkinterDnD.py”, line 55, in _require _tkinter.TclError: can’t find package tkdnd During handling of the above exception, another exception occurred: Traceback (most recent call last): File “1.导入总表…...
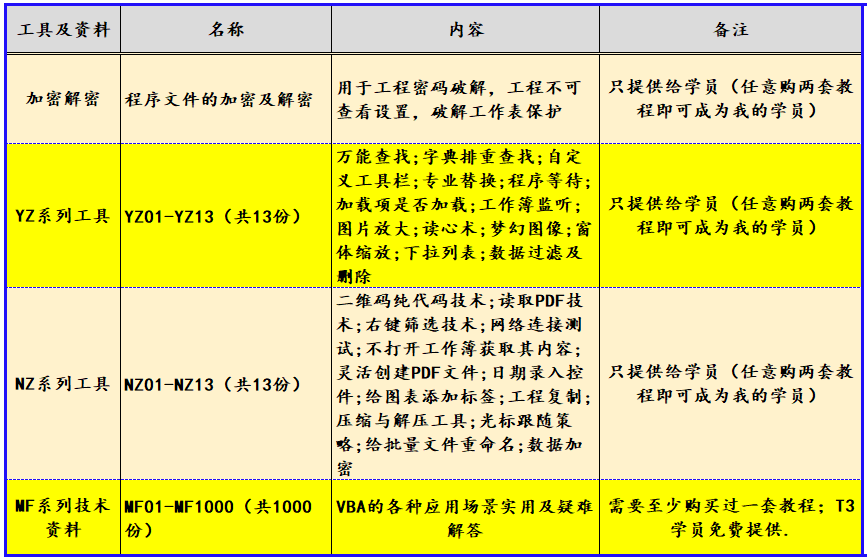
VBA高级应用30例应用在Excel中的ListObject对象:向表中添加注释
《VBA高级应用30例》(版权10178985),是我推出的第十套教程,教程是专门针对高级学员在学习VBA过程中提高路途上的案例展开,这套教程案例与理论结合,紧贴“实战”,并做“战术总结”,以…...

folly库Conv类型转换源码解析
1,普通类型转换 例子1: bool boolV = true;EXPECT_EQ(to<bool>(boolV), true);int intV = 42;EXPECT_EQ(to<int>(intV), 42);float floatV = 4.2f;EXPECT_EQ(to<float>(floatV), 4.2f);double doubleV = 0.42;EXPECT_EQ(to<double>(doubleV), 0.42)…...

UE4 骨骼网格体合并及规范
实现代码 // Fill out your copyright notice in the Description page of Project Settings.#pragma once#include "CoreMinimal.h" #include "SkeletalMeshMerge.h" #include "Kismet/BlueprintFunctionLibrary.h" #include "AceMeshCom…...

Java版企业电子招标采购系统源业码Spring Cloud + Spring Boot +二次开发+ MybatisPlus + Redis
功能描述 1、门户管理:所有用户可在门户页面查看所有的公告信息及相关的通知信息。主要板块包含:招标公告、非招标公告、系统通知、政策法规。 2、立项管理:企业用户可对需要采购的项目进行立项申请,并提交审批,查看所…...

通过源码⼀步⼀步分析 ArrayList 扩容机制
ArrayList 是 Java 中常用的集合类,它底层实现是基于数组的。为了处理元素的动态增加,ArrayList 会在容量不足时进行扩容。以下是通过源码逐步分析 ArrayList 扩容机制的过程。 1. ArrayList 类的基本结构 ArrayList 继承自 AbstractList,实…...

源码分析之Openlayers中默认Controls控件渲染原理
概述 Openlayers 中默认的三类控件是Zoom、Rotate和Attribution 源码分析 defaults方法 Openlayers 默认控件的集成封装在defaults方法中,该方法会返回一个Collection的实例,Collection是一个基于数组封装了一些方法,主要涉及到数组项的添…...

中间件的分类与实践:从消息到缓存
目录 一. 中间件的基本概念 二. 中间件的主要类型 (1)消息中间件(Message-Oriented Middleware, MOM): (2)数据库中间件: (3)Web中间件: &a…...

京东e卡 h5st 4.96
声明: 本文章中所有内容仅供学习交流使用,不用于其他任何目的,抓包内容、敏感网址、数据接口等均已做脱敏处理,严禁用于商业用途和非法用途,否则由此产生的一切后果均与作者无关! 有相关问题请第一时间头像私信联系我删…...
)
《CSS 知识点》滚动条仅在 hover 时才显示(宽度不改变)
很简单! 滚动条的滑动小方块背景色默认透明,仅在hover时设置背景色; 滚动条的轨道背景色默认透明,仅在hover时设置背景色; /*滚动条的滑动小方块*/ ::-webkit-scrollbar-thumb {background: transparent; } /*hover…...

手里有病理切片+单细胞测序的数据,如何开展医工交叉的研究?
小罗碎碎念 这一期推文研究一个问题:病理如何与单细胞结合? 病理与单细胞的结合,时常出现在今年的各大顶刊中。 关于这一领域的研究,其实19年就开始了。我把部分低质量的文献做了剔除,但是也基本能反应这一领域的受关注…...

力矩扭矩传感器介绍
在机械臂(机器人臂)末端使用的力矩扭矩传感器主要用于测量机械臂末端执行器(例如机械手爪、抓取装置等)所受的扭矩和力。这些传感器对机械臂的控制系统至关重要,能够提供精确的力反馈信息,帮助实现更高效、…...

【Appium】AttributeError: ‘NoneType‘ object has no attribute ‘to_capabilities‘
目录 1、报错内容 2、解决方案 (1)检查 (2)报错原因 (3)解决步骤 3、解决结果 1、报错内容 在PyCharm编写好脚本后,模拟器和appium也是连接成功的,但是运行脚本时报错&…...

QT 中 多线程(备查)
基础 一个线程处理窗口事件,其他线程进行逻辑运算 在QT中使用多线程,需要额外注意的: 1)默认的线程在Qt中称之为窗口线程,也叫主线程,负责窗口事件处理或者窗口控件数据的更新 2)子线程负责后台…...

第八十六条:在实现serializable接口时要特别谨慎
要想使一个类的实例可被序列化,非常简单,只要在它的声明中加入"implements Serializable"字样即可。虽然使一个类可被序列化的直接开销低到甚至可以忽略不计,但是为了序列化而付出的长期开销往往是实实在在的。 为实现Serializable…...

【Elasticsearch 中间件】Elasticsearch 客户端使用案例
文章目录 一、安装 Elasticsearch1.1 启动 Elasticsearch1.2 启动 Kibana 二、客户端代码2.1 导入依赖2.2 配置 application.yaml2.3 定义实体类2.4 连接 Elasticserach2.5 定义 Service 层接口2.6 实现 Service 层功能 三、测试项目3.1 添加数据3.2 搜索数据3.3 更新数据3.4 删…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

篇章二 论坛系统——系统设计
目录 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 1. 数据库设计 1.1 数据库名: forum db 1.2 表的设计 1.3 编写SQL 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 通过需求分析获得概念类并结合业务实现过程中的技术需要&#x…...

[拓扑优化] 1.概述
常见的拓扑优化方法有:均匀化法、变密度法、渐进结构优化法、水平集法、移动可变形组件法等。 常见的数值计算方法有:有限元法、有限差分法、边界元法、离散元法、无网格法、扩展有限元法、等几何分析等。 将上述数值计算方法与拓扑优化方法结合&#…...
Android屏幕刷新率与FPS(Frames Per Second) 120hz
Android屏幕刷新率与FPS(Frames Per Second) 120hz 屏幕刷新率是屏幕每秒钟刷新显示内容的次数,单位是赫兹(Hz)。 60Hz 屏幕:每秒刷新 60 次,每次刷新间隔约 16.67ms 90Hz 屏幕:每秒刷新 90 次,…...

Vue 实例的数据对象详解
Vue 实例的数据对象详解 在 Vue 中,数据对象是响应式系统的核心,也是组件状态的载体。理解数据对象的原理和使用方式是成为 Vue 专家的关键一步。我将从多个维度深入剖析 Vue 实例的数据对象。 一、数据对象的定义方式 1. Options API 中的定义 在 Options API 中,使用 …...
