框架建设实战7——定时任务组件
在金融系统中,或者其他对账系统里,往往离不开分布式定时任务。用来做查证或者重试处理。
分布式job目前一般有如下三种:
1.elastic job
当当出品,比较老牌。新公司用的应该不多了。
2.xxl-job
个人开源项目。便于二开;有简洁的后管配置界面,方便接入。
3.powerjob
功能相对全面,至少比xxl-job多了任务编排之类的功能。其基于时间轮的调度模式,还是挺不错的。
我们以xxl-job为例,搭建对应的job组件 : frame-job-starter
1.pom依赖:
<dependency> <groupId>org.springframework.boot</groupId> <artifactId>spring-boot-starter</artifactId> <scope>provided</scope> </dependency> <dependency> <groupId>com.xuxueli</grou相关文章:

框架建设实战7——定时任务组件
在金融系统中,或者其他对账系统里,往往离不开分布式定时任务。用来做查证或者重试处理。 分布式job目前一般有如下三种: 1.elastic job 当当出品,比较老牌。新公司用的应该不多了。 2.xxl-job 个人开源项目。便于二开;有简洁的后管配置界面,方便接入。 3.powerjob …...

mybatis 整合 ehcache
pom.xml <!-- ehcache依赖 --><dependency><groupId>org.mybatis.caches</groupId><artifactId>mybatis-ehcache</artifactId><version>1.1.0</version></dependency>ehcache.xml <?xml version"1.0" en…...
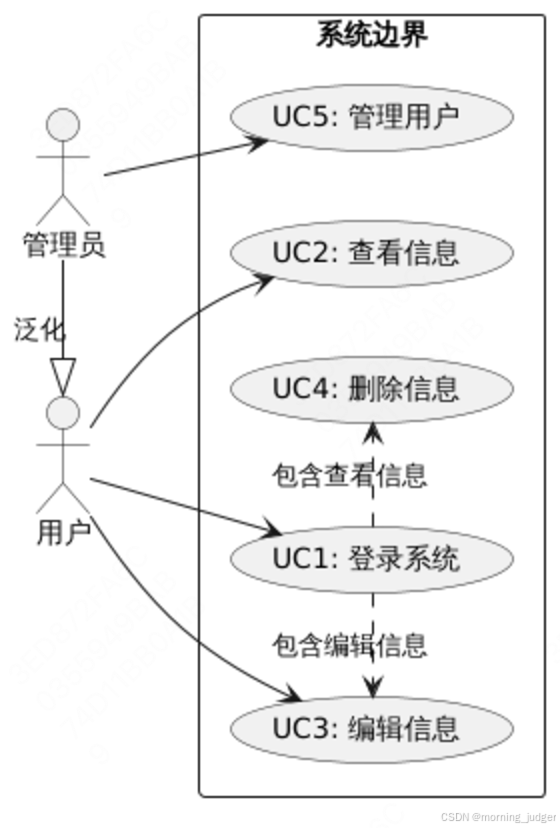
【PlantUML系列】用例图(三)
目录 一、组成部分 二、典型案例 一、组成部分 参与者(Actors):使用关键字 actor 后跟参与者的名称。用例(Use Cases):使用关键字 usecase 后跟用例的名称和编号(可选)。系统边界…...

发送请求时遇到了数据库完整性约束错误 1048 Column ‘platform‘ cannot be null
可以这样解决 在 Vue 2 中封装接口请求时,确保每次请求都包含 platform Header 参数的最佳实践是通过创建一个全局的 Axios 实例,并为这个实例设置默认的 Header。这样可以确保所有通过该实例发送的请求都会自动包含 platform 参数。此外,你…...
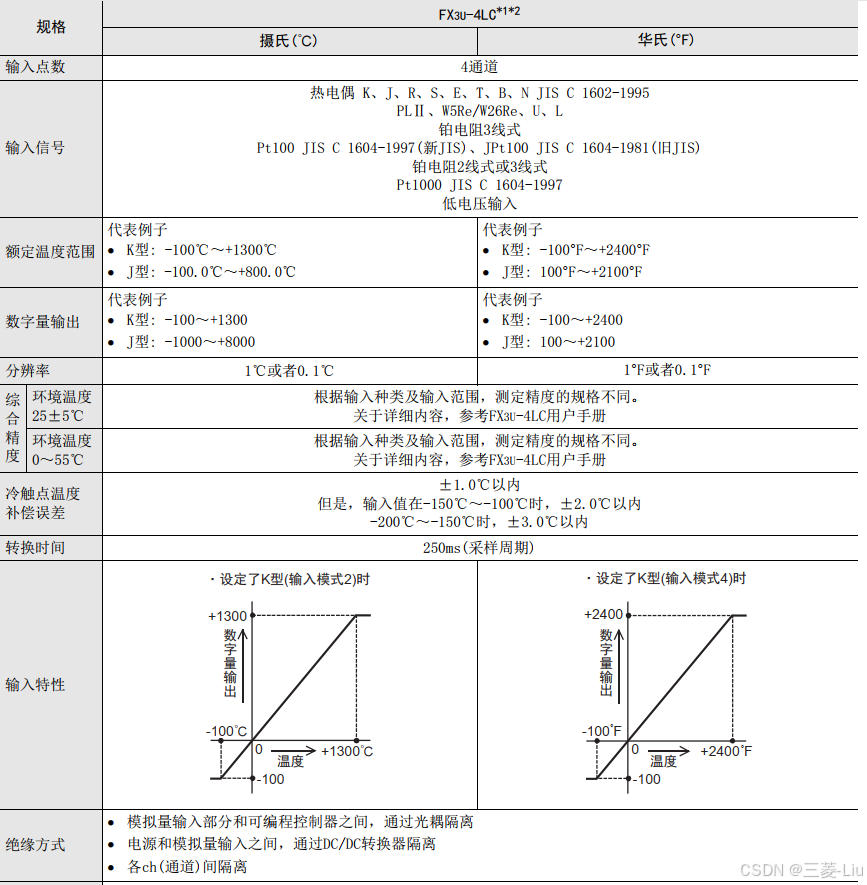
三菱FX3U模拟量产品的介绍
FX3u可编程控制器模拟量产品包括:特殊适配器、特殊功能模块的连接 1、连接在FX3U可编程控制器的左侧。 2、连接特殊适配器时,需要功能扩展板。 3、最多可以连接4台模拟量特殊适配器。 4、使用高速输入输出特殊适配器时,请将模拟量特殊适配器连…...

pdf转图片
目录 pdf2image库 PyMuPDF库 python-office库 pdfplumber库 pdf2image库 安装:pip install pdf2image 使用时会报错:pdf2image.exceptions.PDFInfoNotInstalledError: Unable to get page count. Is poppler installed and in PATH? 需要安装 po…...

Go 协程上下文切换的代价
在 Go 语言中,协程(Goroutine)是一种非常轻量级的并发执行单元,设计之初就是为了简化并发编程并提高性能。协程的上下文切换被认为是非常高效的,但是它的真正性能优势需要我们深入了解其背后的机制。 本文将深入探讨 …...
)
HTTP 持久连接(长连接)
HTTP 持久连接(长连接) HTTP 持久连接(HTTP Persistent Connections),也常被称作 HTTP 长连接,是 HTTP 协议中的一种重要特性,以下是关于它的详细介绍: 一、基本概念 在传统的 HTT…...
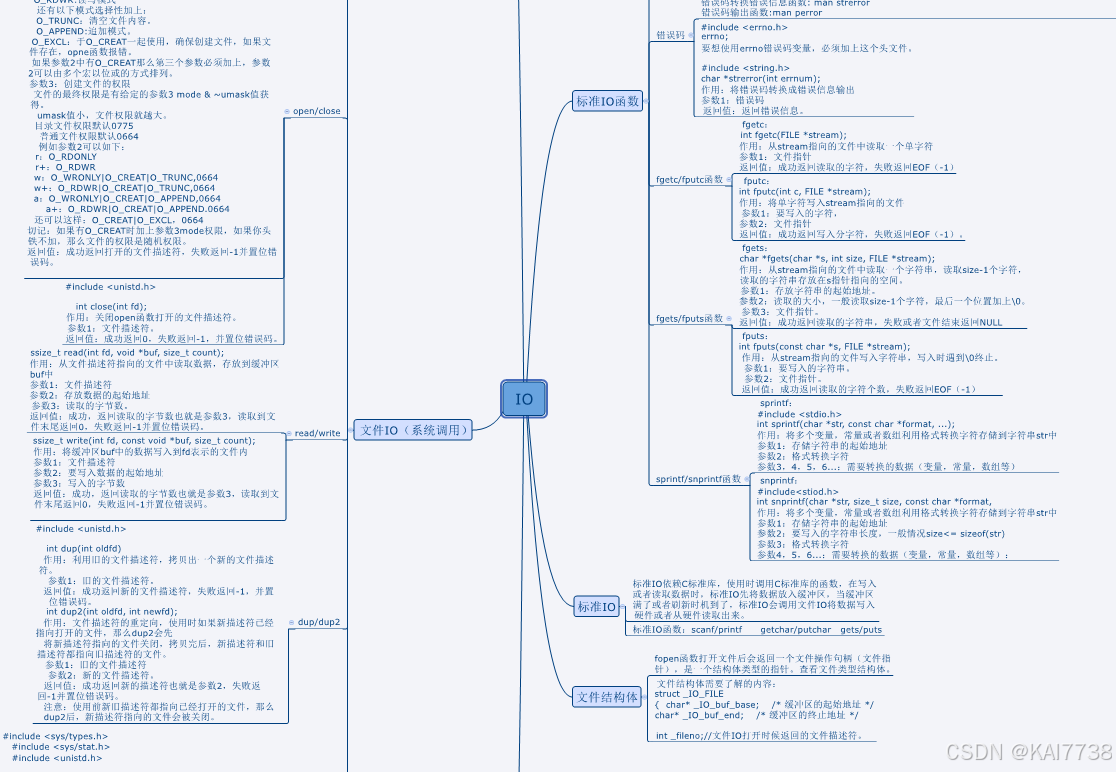
12月10日IO
作业:使用read和write实现拷贝文件,将1.txt内容前一半拷贝给2.txt后一半拷贝给3.txt #include <myhead.h>int main(int argc, const char *argv[]) {//打开三个文件int fd1,fd2,fd3;fd1open("1.txt",O_RDONLY);fd2open("2.txt&quo…...

Composite Pattern
Composite Pattern The intent of Composite pattern is to composite objects into tree structures to represent a “part-whole” hierarchy .The Composite Pattern allow clients to treat individual objects and composite objects uniformly. UML Used in Qt Exam…...

Springboot MVC
1. Springboot为MVC提供的自动配置 Spring Boot 为 Spring MVC 提供了自动配置,这在大多数应用程序中都能很好地工作。除了已经实现了 Spring MVC 的默认功能外,自动配置还提供了以下特性: 包括 ContentNegotiatingViewResolver 和 BeanNam…...

MySQL数据表记录增操作
对数据库的操作用的最最频繁的呢,总结起来就四个字:增删改查! 查是属于DQL(Data QueryLanguage ,数据查询语言)部分,而增、改、删属于DML(Data Manipulation Language, 数据操纵语言) 增:作用是往数据库的数据表里写入记录值 语…...
maven报错“找不到符号“
问题 springboot项目 maven编译打包过程,报错"找不到符号" 解决 很多网上方法都试过,都没用 换jdk,把17->21...
python进阶-05-利用Selenium来实现动态爬虫
python进阶-05-利用Selenium来实现动态爬虫 一.说明 这是python进阶部分05,我们上一篇文章学习了Scrapy来爬取网站,但是很多网站需要登录才能爬取有用的信息,或者网站的静态部分是一个空壳,内容是js动态加载的,或者人机验证&…...

P1226 【模板】快速幂
题目描述 给你三个整数 𝑎,𝑏,𝑝求 𝑎𝑏 mod 𝑝 输入格式 输入只有一行三个整数,分别代表 𝑎,𝑏,𝑝 输出格式 输出一行一个字符串 a^b mod ps…...

【C++】求第二大的数详细解析
博客主页: [小ᶻ☡꙳ᵃⁱᵍᶜ꙳] 本文专栏: C 文章目录 💯前言💯题目描述💯输入描述💯解题思路分析1. 题目核心要求2. 代码实现与解析3. 核心逻辑逐步解析定义并初始化变量遍历并处理输入数据更新最大值与次大值输…...
从零开始学TiDB(3)TiKV 持久化机制
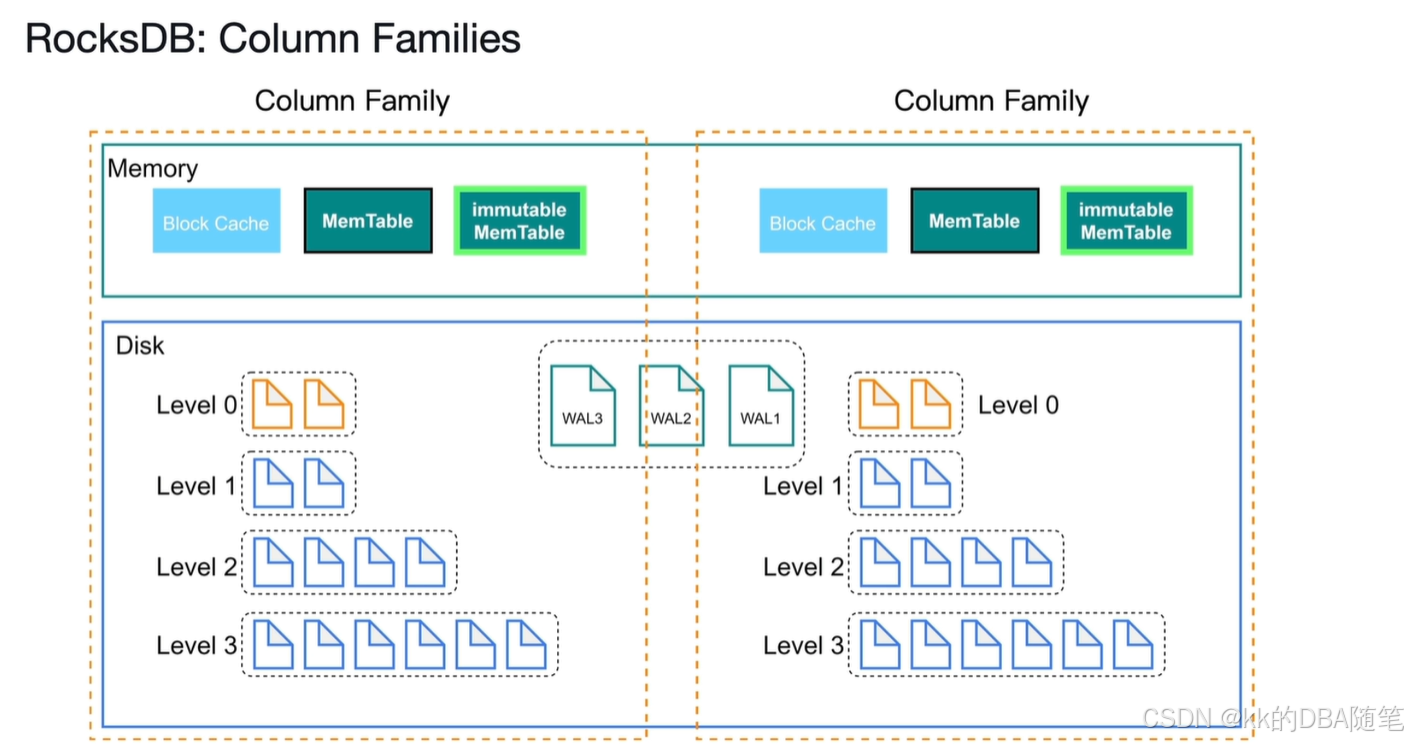
如图,每个TiKV有两个rocksdb实例,rocksdbKV复制存储键值对,rocksdb raft负责存储复制的日志 。 每个region及其副本构成了raft group。这个OB的Zone其实有点类似,在OB中每个Unit及其副本构成了paxos组,在TiDB中叫raft…...

Elasticsearch+Kibana+IK分词器+拼音分词器安装
目录 ES报错 Kibanaik分词器拼音分词器 安装都比较简单,可以参考这几篇博客 ES 如何在 Linux,MacOS 及 Windows 上进行安装 Elasticsearch 报错 ES启动报错error downloading geoip database [GeoLite2-ASN.mmdb] Kibana KIBANA的安装教程ÿ…...
子网划分实例
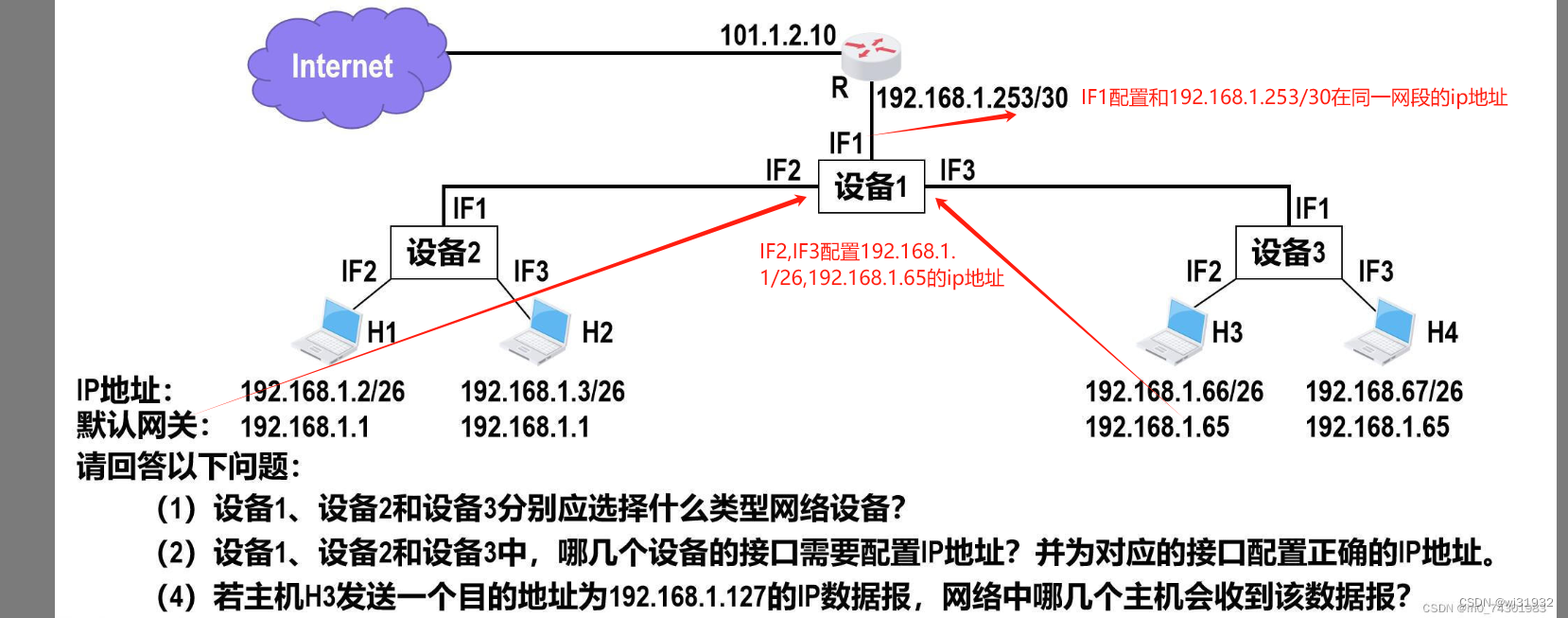
看到有人问这个问题: 想了一下,这是一个子网划分的问题: 处理方法如图: 这是一个子网划分的问题 设备1用三层交换机,端口设置为路由模式,设备2和设备3为傻瓜交换机模式 设备2和设备3下挂设备都是26为掩码&…...

上海亚商投顾:创业板指震荡调整 机器人概念股再度爆发
上海亚商投顾前言:无惧大盘涨跌,解密龙虎榜资金,跟踪一线游资和机构资金动向,识别短期热点和强势个股。 一.市场情绪 沪指昨日冲高回落,深成指、创业板指盘中跌超1%,尾盘跌幅有所收窄。机器人概念股逆势爆…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...
