【C++】求第二大的数详细解析

文章目录
- 💯前言
- 💯题目描述
- 💯输入描述
- 💯解题思路分析
- 1. 题目核心要求
- 2. 代码实现与解析
- 3. 核心逻辑逐步解析
- 定义并初始化变量
- 遍历并处理输入数据
- 更新最大值与次大值
- 输出结果
- 4. 示例分析
- 示例输入
- 示例输出
- 数据处理过程
- 💯高级拓展与优化分析
- 时间与空间复杂度
- 潜在错误与改进方向
- 数学与工程意义
- 💯多种解法的对比与讨论
- 排序法
- 分治法
- 💯小结

💯前言
- 在计算机科学和算法设计领域,如何以最优的方式处理有限的资源和数据一直是一个重要的研究课题。针对这一问题,本次探讨围绕一个经典的编程挑战展开:
寻找数列中的次大值。本题虽然在描述上简洁,但通过限制变量和数据结构的使用,从而将重点放在动态维护状态变量和优化算法性能上。这不仅为基础算法设计提供了宝贵的训练机会,同时也为解决实际工程中的资源约束问题提供了可借鉴的思路。
本次分析将从题目背景、算法设计、代码实现、扩展优化及多解法对比等多个角度,系统地探讨这一问题的本质及其实现方法。
C++ 参考手册

💯题目描述
![]()
数学里有一个函数定义为 max(a, b),它返回 a 和 b 中较大的那个值。基于这一定义,现要求完成一个函数 max2,旨在从当前已经处理过的所有输入数字中,返回次大值。
需要注意的是,本题对代码实现有如下明确限制:
- 只能使用两个全局变量
a1和a2分别记录当前最大值和次大值。 - 不允许使用数组或其他结构存储所有输入的数字。
- 允许额外使用两个局部变量用于存储整数个数 n 和当前输入的整数。
💯输入描述
![]()
第一行输入一个整数 n,表示有 n 个正整数满足 2 ≤ n ≤ 100 2 \leq n \leq 100 2≤n≤100。
第二行输入 n 个互不相等的正整数。
输出描述
输出仅包含一个整数,即输入数列中的次大值。
示例1
输入:
10
10 9 8 7 6 5 4 3 2 1
输出:
9
💯解题思路分析
![]()
1. 题目核心要求
![]()
本题的核心在于从输入数据中以高效方式求解次大值,同时遵守以下条件约束:
- 输入正整数各不相同,保证了最大值和次大值的存在性。
- 只能使用两个变量
a1和a2存储结果状态,考验算法设计对空间资源的优化。 - 需要保证算法能够在线性时间内完成计算,即时间复杂度为 O ( n ) O(n) O(n)。
2. 代码实现与解析
以下是问题的完整代码实现:
#include <iostream>
using namespace std;
#include <climits>void max2() {int n;cin >> n; // 读取正整数个数int a1 = INT_MIN; // 最大值初始化为最小整数int a2 = INT_MIN; // 次大值初始化为最小整数for (int i = 0; i < n; ++i) {int num;cin >> num; // 逐一读取每个正整数if (num > a1) {// 当前数字比最大值大,则更新最大值和次大值a2 = a1;a1 = num;} else if (num > a2) {// 当前数字介于最大值和次大值之间,更新次大值a2 = num;}}cout << a2 << endl; // 输出次大值
}int main() {max2();return 0;
}

3. 核心逻辑逐步解析
![]()
定义并初始化变量
![]()
int a1 = INT_MIN;
int a2 = INT_MIN;
- 目的:
a1用于记录当前的最大值。a2用于记录当前的次大值。- 初始化为
INT_MIN,以确保任何正整数输入都可以覆盖初始值。
遍历并处理输入数据
![]()
for (int i = 0; i < n; ++i) {int num;cin >> num;
- 使用
for循环逐一读取正整数,并对每个输入值进行处理。 - 每次读取到的新数字需要根据与
a1和a2的关系进行条件判断。
更新最大值与次大值
![]()
if (num > a1) {a2 = a1;a1 = num;
} else if (num > a2) {a2 = num;
}
- 逻辑分析:
- 当
num > a1时:- 原最大值
a1退化为次大值a2。 - 新数字
num成为新的最大值a1。
- 原最大值
- 当
num位于最大值a1和次大值a2之间时:- 更新
a2为当前数字num。
- 更新
- 当
输出结果
![]()
cout << a2 << endl;
- 循环结束后,
a2中存储的是次大值,直接输出。
4. 示例分析

示例输入
![]()
10
10 9 8 7 6 5 4 3 2 1
示例输出
![]()
9
数据处理过程
![]()
| 迭代次数 | 当前数字 (num) | 最大值 (a1) | 次大值 (a2) |
|---|---|---|---|
| 1 | 10 | 10 | INT_MIN |
| 2 | 9 | 10 | 9 |
| 3 | 8 | 10 | 9 |
| … | … | … | … |
| 10 | 1 | 10 | 9 |
最终结果:次大值为 9。
💯高级拓展与优化分析
![]()
时间与空间复杂度
![]()
- 时间复杂度:
- 对输入数据的单次遍历,复杂度为 O ( n ) O(n) O(n),与数据规模呈线性关系。
- 空间复杂度:
- 仅使用两个额外变量
a1和a2,复杂度为 O ( 1 ) O(1) O(1)。
- 仅使用两个额外变量
潜在错误与改进方向
![]()
-
初始化问题
- 如果未正确初始化
a1和a2,例如初始化为0,在输入为负数时会导致错误。 - 为避免此类问题,需始终选择合适的初始值,例如
INT_MIN。
- 如果未正确初始化
-
边界条件处理
- 当 ( n = 2 ) 时,代码需要保证能够正确处理这类极小输入规模的场景。
-
逻辑健壮性
- 对于更复杂的输入场景(如输入中存在重复值或非法值),需增加必要的输入校验逻辑。
数学与工程意义
![]()
从数学角度来看,本题的核心问题是动态维护“前两大值”。这类问题在实际工程中有广泛应用,例如:
- 流式数据处理:实时更新数据流的统计特性。
- 排名问题:动态维护某指标的前 k 个最大值。
在资源受限的场景下(如嵌入式设备或内存有限的系统),设计类似的轻量级算法尤为重要。
💯多种解法的对比与讨论
![]()
排序法
- 思路:对输入数据排序,取倒数第二个值。
- 时间复杂度: O ( n log n ) O(n \log n) O(nlogn)。
- 缺点:额外的空间和时间开销。

分治法
- 思路:递归分组寻找最大值和次大值。
- 时间复杂度:接近 O ( n ) O(n) O(n)。
- 缺点:代码复杂度较高,且在小规模数据上优势不明显。

💯小结

通过本题,我们可以清晰认识到在有限资源条件下,如何设计高效算法以满足问题需求。这不仅考察了程序的正确性,还着重强调了代码的优化能力和设计美感。
这种能力的培养需要长期的练习和理论积累,同时在不同场景中总结经验。更重要的是,这类问题的解决思路能够拓展到更广泛的工程实践中,例如实时数据分析、大规模流数据处理等领域,为构建更高效的系统打下坚实基础。

相关文章:

【C++】求第二大的数详细解析
博客主页: [小ᶻ☡꙳ᵃⁱᵍᶜ꙳] 本文专栏: C 文章目录 💯前言💯题目描述💯输入描述💯解题思路分析1. 题目核心要求2. 代码实现与解析3. 核心逻辑逐步解析定义并初始化变量遍历并处理输入数据更新最大值与次大值输…...
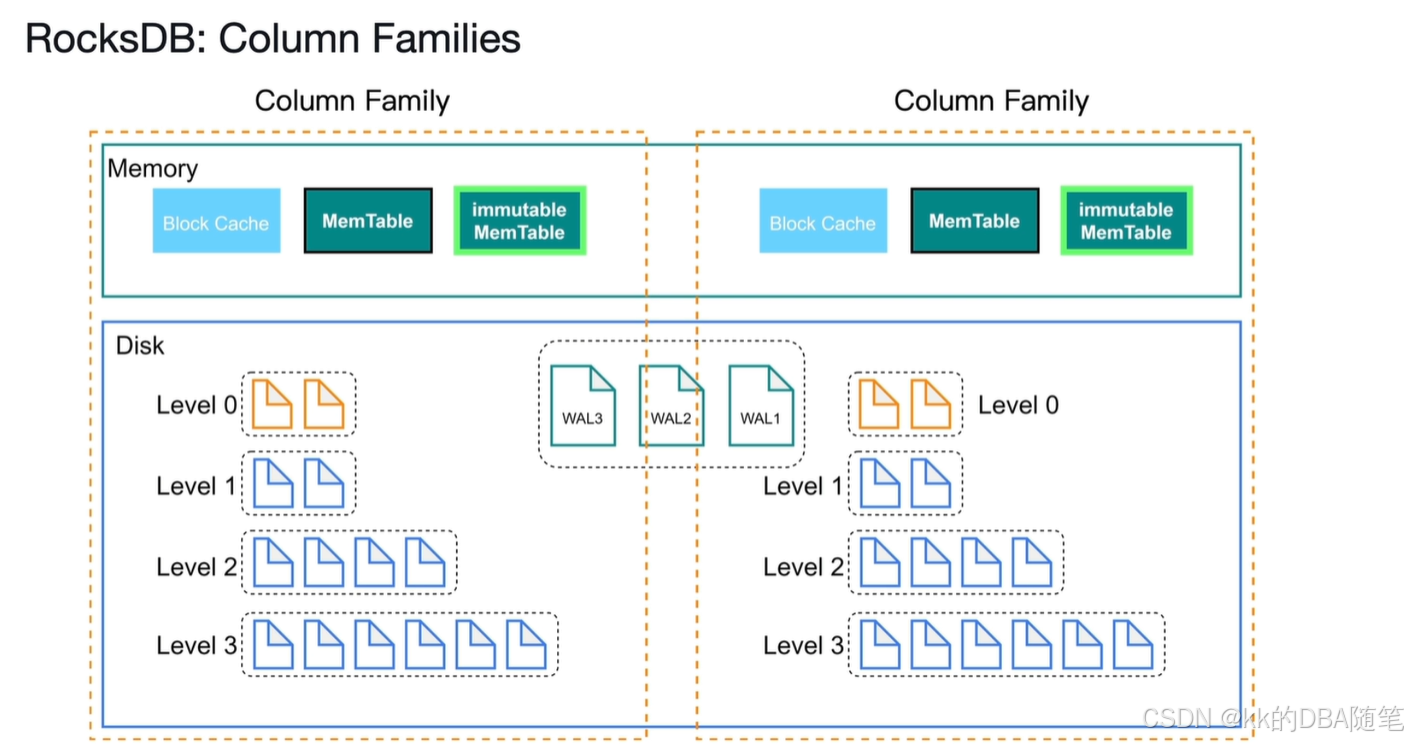
从零开始学TiDB(3)TiKV 持久化机制
如图,每个TiKV有两个rocksdb实例,rocksdbKV复制存储键值对,rocksdb raft负责存储复制的日志 。 每个region及其副本构成了raft group。这个OB的Zone其实有点类似,在OB中每个Unit及其副本构成了paxos组,在TiDB中叫raft…...

Elasticsearch+Kibana+IK分词器+拼音分词器安装
目录 ES报错 Kibanaik分词器拼音分词器 安装都比较简单,可以参考这几篇博客 ES 如何在 Linux,MacOS 及 Windows 上进行安装 Elasticsearch 报错 ES启动报错error downloading geoip database [GeoLite2-ASN.mmdb] Kibana KIBANA的安装教程ÿ…...
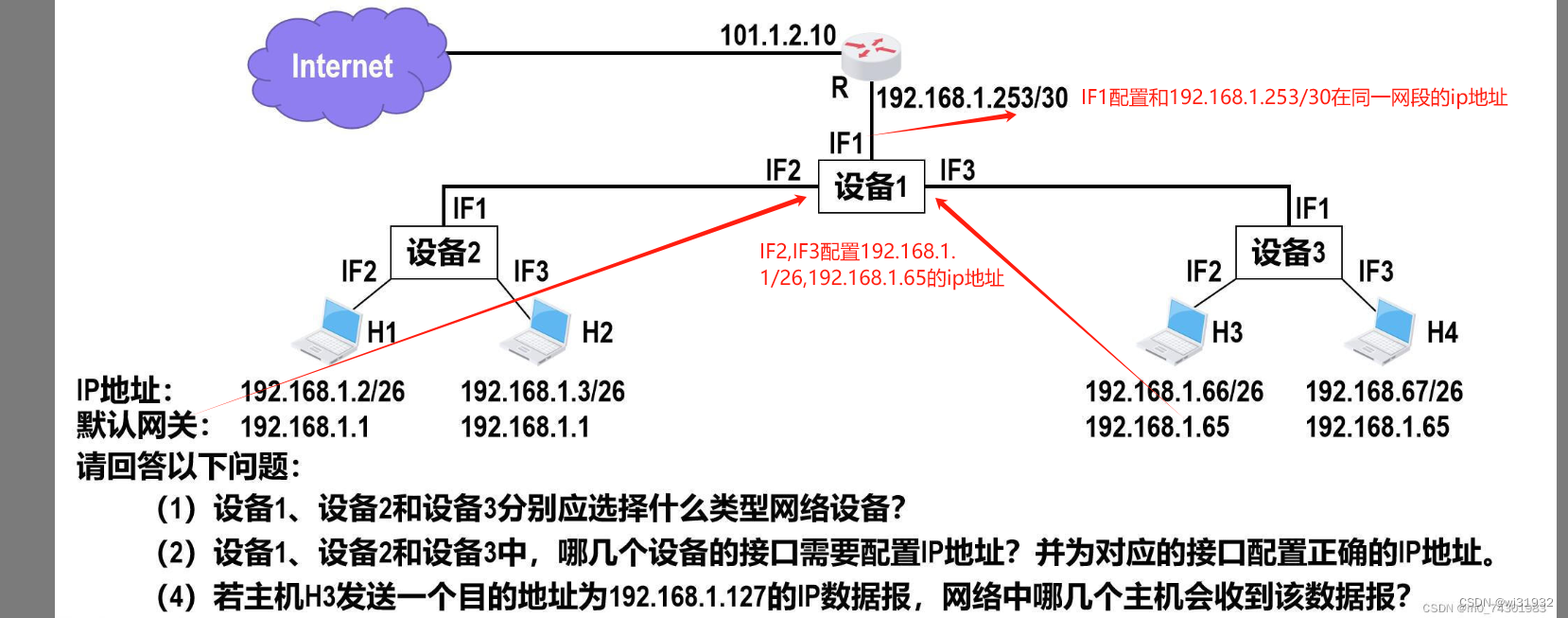
子网划分实例
看到有人问这个问题: 想了一下,这是一个子网划分的问题: 处理方法如图: 这是一个子网划分的问题 设备1用三层交换机,端口设置为路由模式,设备2和设备3为傻瓜交换机模式 设备2和设备3下挂设备都是26为掩码&…...

上海亚商投顾:创业板指震荡调整 机器人概念股再度爆发
上海亚商投顾前言:无惧大盘涨跌,解密龙虎榜资金,跟踪一线游资和机构资金动向,识别短期热点和强势个股。 一.市场情绪 沪指昨日冲高回落,深成指、创业板指盘中跌超1%,尾盘跌幅有所收窄。机器人概念股逆势爆…...
:初始化 Initializer)
【C++ 20进阶(2):初始化 Initializer
【C 20进阶(2):初始化 Initializer】 原文:https://blog.csdn.net/weixin_44259356/article/details/144377955 引言 本篇文章为系列文章将着重介绍C20新特性,一是希望可以和大家交流分享,二是也便于自己…...

【重生之我在B站学MySQL】
MySQL笔记 文章目录 MySQL的三层结构SQL语句分类sql语句数据库操作创建数据库查看、删除数据库 表操作创建表mysql常用数据类型(列类型)查询表、插入值创建表练习创建一个员工表emp 修改表mysql约束primary key(主键)not null(非空)unique(唯一)foreign key(外键)check自增长 索…...

Python实现中国象棋
探索中国象棋 Python 代码实现:从规则逻辑到游戏呈现 中国象棋,这款源远流长的棋类游戏,承载着深厚的文化底蕴与策略智慧。如今,借助 Python 与 Pygame 库,我们能够在数字世界中复刻其魅力,深入探究代码背后…...
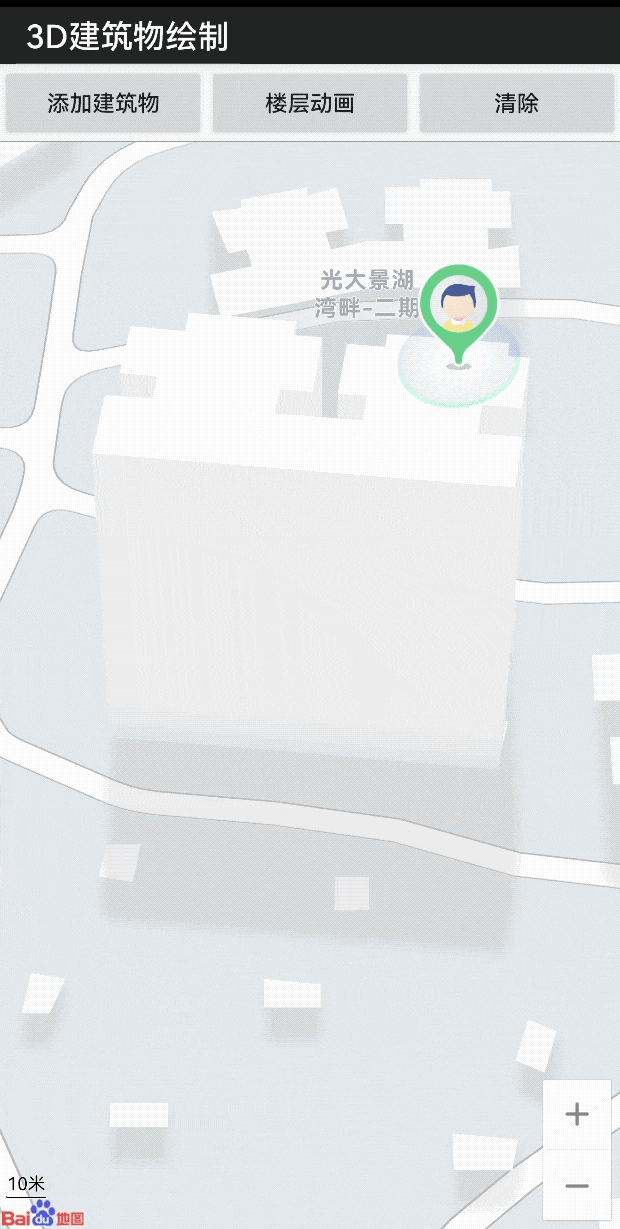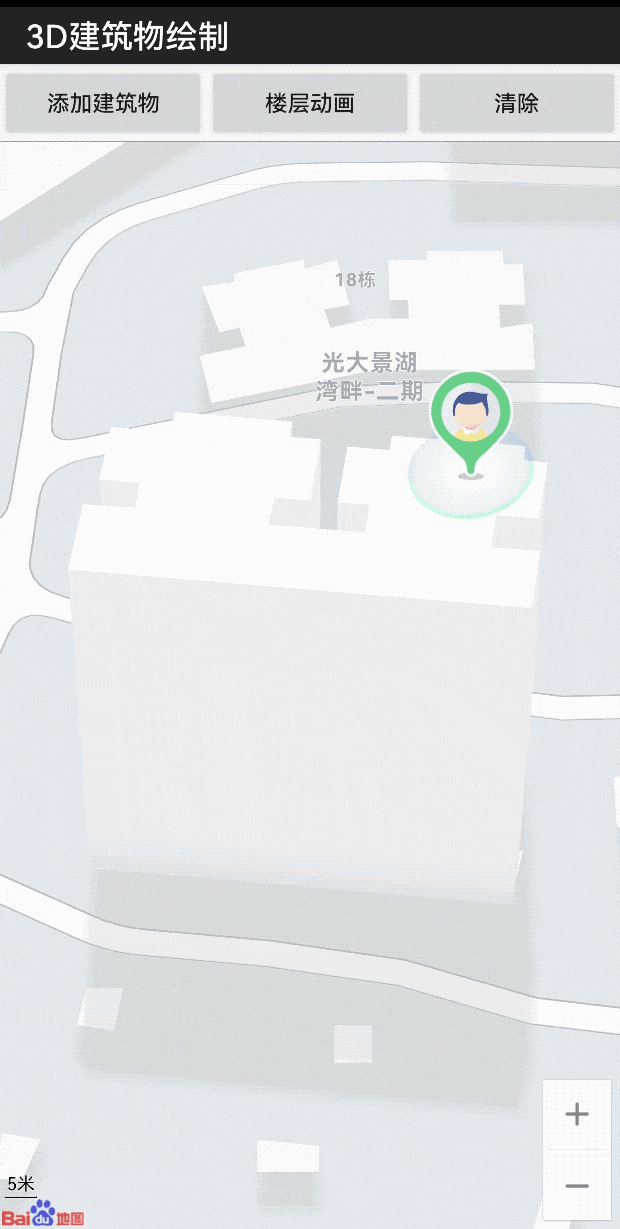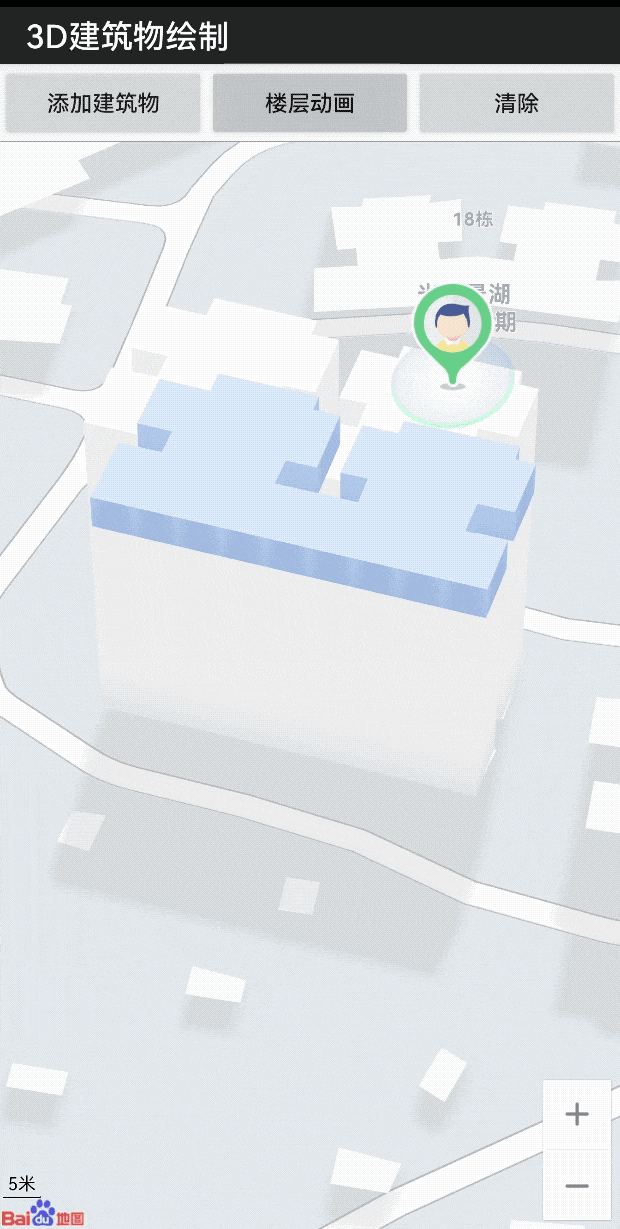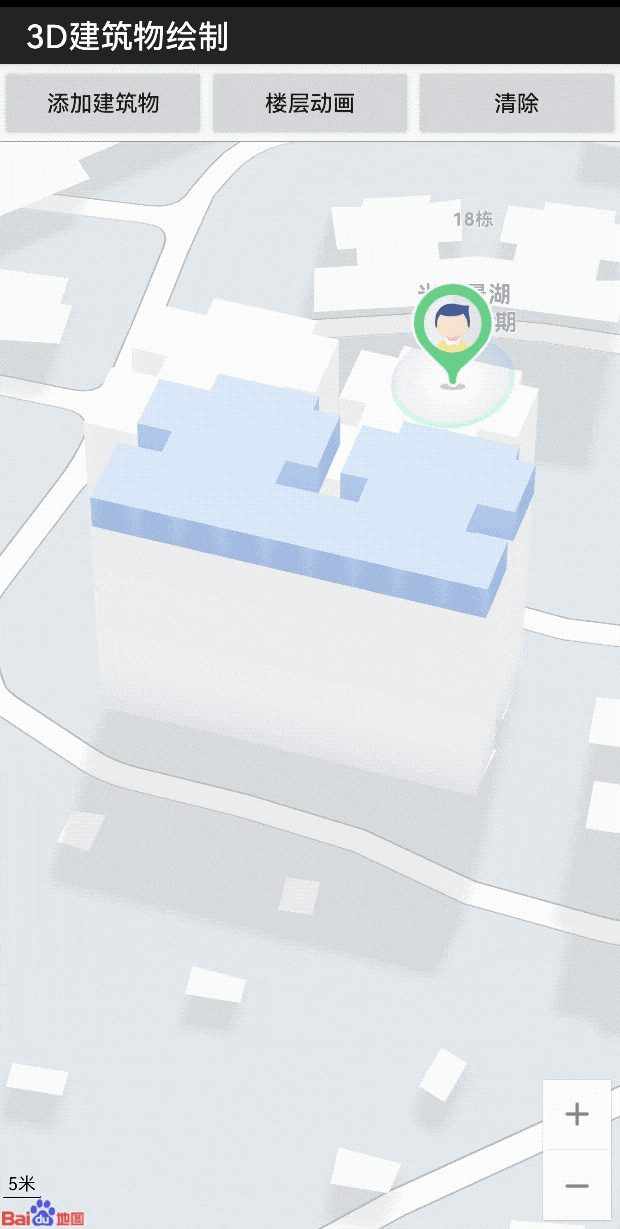
LBS 开发微课堂|通过openGL ES轻松实现建筑物渲染及动画
为了让广大开发者 更深入地了解 百度地图开放平台的 技术能力 轻松掌握满满的 技术干货 更加简单地接入 位置服务 我们特别推出了 “位置服务(LBS)开发微课堂” 系列技术案例 第五期的主题是 通过openGL ES轻松实现 建筑物渲染及动画 对于…...
的区别为何前者取出的是空,后者取出的是正确的值)
map1[item.id]和map1.get(item.id)的区别为何前者取出的是空,后者取出的是正确的值
在 JavaScript 中,map1[item.id] 和 map1.get(item.id) 用于从 Map 对象中获取值,但它们的工作方式有所不同: map1[item.id]:这种方式用于普通对象(Object),它将 item.id 作为键来获取对应的值…...

window端sqlplus连接linux_oracle11g
1. 环境配置回顾 下载 Oracle Instant Client:根据查询到的版本到链接: oracle官网下载对应版本的三个文件(比如我这里查询到的版本是12.2.0.1.0): instantclient-basic-windows.x64-12.2.0.1.0.zip instantclient-sqlplus-win…...

Go支付中台方案:多平台兼容与多项目对接
一、中台的概念 中台是一种企业级的架构模式,它处于前台应用和后台资源之间,将企业核心能力进行整合、封装,形成一系列可复用的业务能力组件。这些组件就像乐高积木一样,可以被不同的前台业务快速调用,从而避免重复开…...

MySQL触发器的使用详解
MySQL触发器的使用详解 MySQL触发器是一种特殊的存储过程,它与表操作紧密相关,并且在特定事件(如INSERT、UPDATE或DELETE)发生时自动执行。触发器的主要目的是确保数据完整性、实现复杂的业务逻辑以及记录审计信息。它们可以在事…...

关于NLP交互式系统的一些基础入门
【1】What 基于自然语言处理(NLP)的交互式系统是指能够理解、解析并生成人类自然语言的计算机程序。这些系统旨在通过文本或语音与用户进行交流,以提供信息、解决问题或执行任务。以下是关于这类系统的一些关键点: 核心技术&…...
)
如何在HTML中修改光标的位置(全面版)
如何在HTML中修改光标的位置(全面版) 在Web开发中,控制光标位置是一个重要的技巧,尤其是在表单处理、富文本编辑器开发或格式化输入的场景中。HTML中的光标位置操作不仅适用于表单元素(如<input>和<textarea…...

PHP8 动态属性被弃用兼容方案
PHP 类中可以动态设置和获取没有声明过的类属性。这些属性不遵循具体的规则,并且需要使用 __get() 和 __set() 魔术方法对动态属性如何读写进行有效控制。 class User {private int $uid; }$user new User(); $user->name Foo; 上述代码中,User 类…...
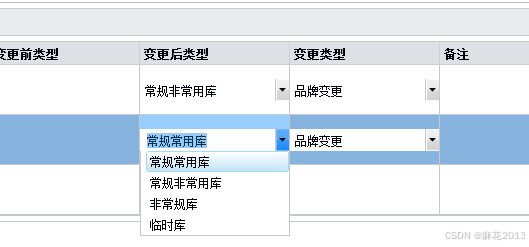
WPF表格控件的列利用模块适配动态枚举类
将枚举列表转化到类内部赋值,在初始化表格行加载和双击事件时,触发类里面的枚举列表的赋值 <c1:Column Header"变更类型" Binding"{Binding ChangeType, ModeTwoWay, ValidatesOnExceptionsTrue, ValidatesOnDataErrorsTrue, NotifyOn…...
【sgUploadImage】自定义组件:基于elementUI的el-upload封装的上传图片、相片组件,适用于上传缩略图、文章封面
sgUploadImage源码 <template><div :class"$options.name"><ul class"uploadImages"><liclass"uploadImage"v-loading"loadings[i]"v-for"(a, i) in uploadImages":key"i"click"click…...

Scala的隐式转换
一: 1.隐式转换概述: 隐式转换与模式匹配都是scala中提供的比较强大的特性。 2.隐式转换的定义: 在实际编程中,要想把一个不匹配的类型赋值,需要先转换成匹配的类型。scala的隐式转换会自动将一种类型的数据转换成…...

从视频编码的进化历程看技术革新
人类对影像的记录和传播从未停止。从最早的胶片电影到如今的数字视频,技术在不断演进。在这个过程中,视频编码技术的发展扮演着关键角色,它决定着我们如何高效地存储和传输视频内容。 视频编码技术的发展历程充满智慧。上世纪90年代…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...
