MATLAB中circshift函数的原理分析——psf2otf函数的核心
之所以讲到MATLAB中circshift函数,也是源于Rafael Gonzalez的这个图,作为前几篇答廖老师问的blog的基础。
Rafael Gonzalez的这个图无论从哪幅图到哪幅图都不是直接的傅里叶变换或傅里叶逆变换,需要循环移位,即circshift函数。

这就需要从头说起。
离散时间傅里叶变换(DTFT)的一个性质是,如果一个序列共轭对称,即 x [ n ] = x ∗ [ − n ] x[n] = x^*[-n] x[n]=x∗[−n],那么它的傅里叶变换是实数。因此,当fft函数的输出结果出乎意料地为复数时,人们有时会感到惊讶。
用实序列说明。当输入序列是实偶对称时,其傅里叶变换的输出序列也是实数且偶对称的。
例如:
n = -3:3;
x = exp(-abs(n)/2)x =0.2231 0.3679 0.6065 1.0000 0.6065 0.3679 0.2231
这个序列看起来是对称的,但当我们计算fft(x)时,其输出却是复数。
>> X = fft(x)X =列 1 至 53.3951 + 0.0000i -1.0726 - 0.5166i 0.2154 + 0.2701i -0.0593 - 0.2598i -0.0593 + 0.2598i列 6 至 70.2154 - 0.2701i -1.0726 + 0.5166i原因是fft函数计算的是在区间 0 ≤ n < N 0 \leq n < N 0≤n<N内非零的序列 x [ n ] x[n] x[n]的离散傅里叶变换。实际上, x [ n ] x[n] x[n]并不是关于原点对称的,它是一个对称序列的移位版本,而这种移位导致了fft的输出为复数。
为了得到实数值的傅里叶变换,我们需要将序列循环移位,使中心元素移动到向量的左边。对于长度为奇数或偶数的序列,我们都可以使用以下方法来找到中心位置,并进行相应的循环移位:
xs = circshift(x, [0 -floor(length(x)/2)]);
xs =1.0000 0.6065 0.3679 0.2231 0.2231 0.3679 0.6065现在,如果我们计算 fft(xs),将会得到预期的实数输出。
>> Xs = fft(xs)Xs =3.3951 1.1905 0.3454 0.2665 0.2665 0.3454 1.1905
结合之前讲的循环移位,用这幅图解释,循环移位后是最后的结果,但是对应于第三幅中中心在原点的情况,这才是偶函数。

如果打算进行零填充(zero-padding),应该先填充再应用循环移位(这里很关键,我曾经在这里错过,百思不得其解,思考了数年之久)。下面是一个示例,其中我们将原始序列扩展到长度为128,并对其进行处理:
x128 = x;
x128(128) = 0; % 零填充到长度128
x128s = circshift(x128, [0 -floor(length(x)/2)]); % 循环移位
X128 = fft(x128s);
检查是否为实数:
isreal(X128)ans =logical0
这里可能会出现一个小的误差,认为这个过程不能产生实数结果,但实际上是因为浮点舍入误差。查看虚部的大小可以发现它们非常小:
max(abs(imag(X128(:))))ans =2.1252e-16
可以使用real函数去除可以忽略不计的虚部。下面是绘制实值傅里叶变换的方法。我将使用频率轴标记技术来展示结果:
w = unwrap(fftshift(2*pi * (0:(128-1)) / 128) - 2*pi);
figure; plot(w/pi, fftshift(real(X128)), "LineWidth", 1);
xlabel('弧度 / \pi');
box off;
grid on;

相关文章:

MATLAB中circshift函数的原理分析——psf2otf函数的核心
之所以讲到MATLAB中circshift函数,也是源于Rafael Gonzalez的这个图,作为前几篇答廖老师问的blog的基础。 Rafael Gonzalez的这个图无论从哪幅图到哪幅图都不是直接的傅里叶变换或傅里叶逆变换,需要循环移位,即circshift函数。 这…...

js 惰性函数
惰性函数 是一种优化技术,主要用于避免重复判断和计算。它在第一次调用时确定最终的执行逻辑,并将其替换为适当的函数实现,从而在后续调用中跳过不必要的判断或初始化。 惰性函数的核心思想 第一次调用时执行初始化逻辑,并根据环…...

智能技术引领未来:自动图像标注的创新应用与发展
🍑个人主页:Jupiter. 🚀 所属专栏:传知代码 欢迎大家点赞收藏评论😊 目录 概述算法原理核心逻辑效果演示使用方式参考文献 参考文献:需要本文的详细复现过程的项目源码、数据和预训练好的模型可从该地址处获…...

深入探索数据库世界:SQLite、Redis、MySQL 与数据库设计范式
数据库 深入探索数据库世界:SQLite、Redis、MySQL 与数据库设计范式一、SQLite 数据库全方位解析(一)创建与基本操作(二)数据存储与表结构设计(三)数据操作:增删改查(四)与 C 语言联合使用(五)防止 SQL 注入二、Redis 数据库深度剖析(一)数据存储类型与独特结构(…...

内网是如何访问到互联网的(华为源NAT)
私网地址如何能够访问到公网的? 在上一篇中,我们用任意一个内网的终端都能访问到百度的服务器,但是这是我们在互联网设备上面做了回程路由才实现的,在实际中,之前也说过运营商是不会写任何路由过来的,那对于…...

华为无线AC、AP模式与上线解析(Huawei Wireless AC, AP Mode and Online Analysis)
华为无线AC、AP模式与上线解析 为了实现fit 瘦AP的集中式管理,我们需要统一把局域网内的所有AP上线到AC,由AC做集中式管理部署。这里我们需要理解CAPWAP协议,该协议分为两种报文:1、管理报文 2、数据报文。管理报文实际在抓包过程…...

奖励模池化
奖励模池化 奖励模型概述 奖励模型(Reward Model)在机器学习,特别是强化学习领域中被广泛使用。它的主要作用是**对智能体(Agent)的行为进行评估并给予奖励。**例如,在训练一个机器人执行任务时,当机器人的动作符合预期目标(如成功抓取物品、按照正确路线行走等),奖励…...

基于django协同过滤的音乐推荐系统的设计与实现
一、摘要 随着现代音乐的快速发展,协同过滤的音乐推荐系统已成为人们业余生活的需求。该平台采用Python技术和django搭建系统框架,后台使用MySQL数据库进行信息管理;通过用户管理、音乐分类管理、音乐信息管理、歌曲数据管理、系统管理、我的…...

Tiptap,: 富文本编辑器入门与案例分析
Tiptap 是一个现代的富文本编辑器,基于 ProseMirror 打造,旨在提供一个灵活且功能强大的文本编辑解决方案。它具有开箱即用的能力,同时也允许开发者根据业务需求进行高度定制化扩展。与传统的富文本编辑器相比,Tiptap 提供了更精细…...
)
使用Linux的logrotate工具切割日志:Tomcat、NGINX(journal文件清理)
文章目录 引言I Tomcat日志切割配置轮转参数验证码II NGINX访问文件的配置和切割access.log 访问日志的配置使用Linux的logrotate工具切割日志验证文件切割III /run/log/journaljournalctl文件清理引言 journal文件清理: 只保留过去两天,清理之前的文件 journalctl --vacuu…...
-- 滤镜与混合模式详解)
CSS系列(11)-- 滤镜与混合模式详解
前端技术探索系列:CSS 滤镜与混合模式详解 🎨 致读者:探索视觉效果的艺术 👋 前端开发者们, 今天我们将深入探讨 CSS 滤镜与混合模式,学习如何创建独特的视觉效果。 滤镜效果详解 🚀 基础滤…...

linux - 存储管理
1.了解硬件 -- 磁盘 硬盘有机械硬盘(HDD)和固态硬盘(SDD) 接下来,主要以机械磁盘为例(更具代表性,在linux系统层面,无论是机械磁盘还是固态硬盘,文件的读取和写入都iNode(索引节点)管理文件的元数据和实际数据块) 1.盘片&#x…...
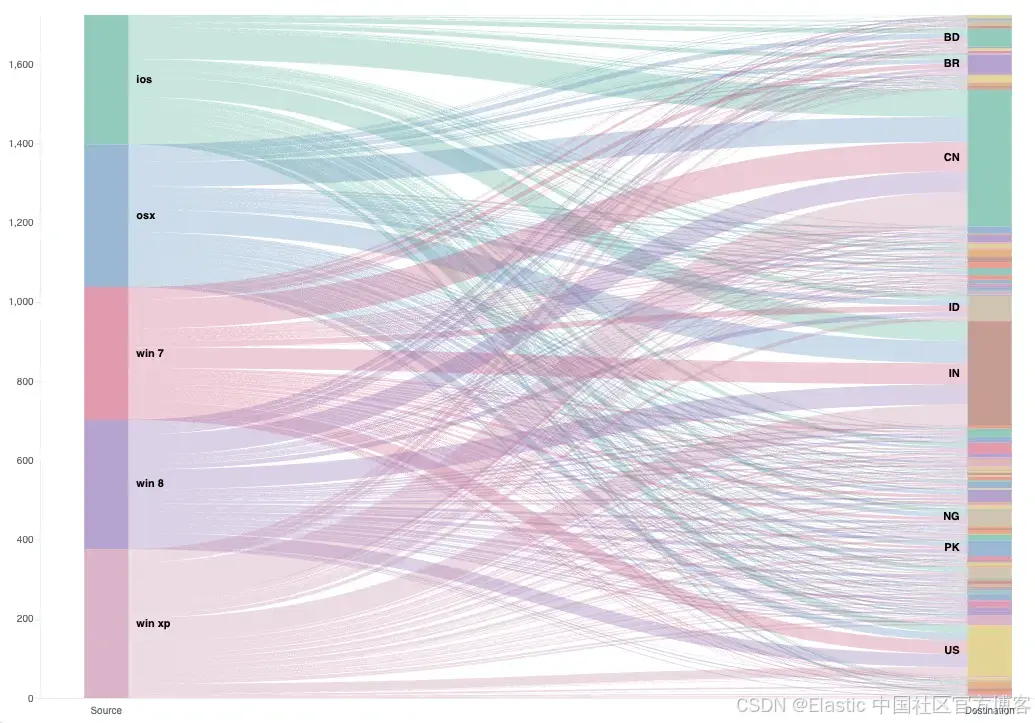
在 Kibana 中为 Vega Sankey 可视化添加过滤功能
作者:来自 Elastic Tim Bosman 及 Miloš Mandić 有兴趣在 Kibana 中为 Vega 可视化添加交互式过滤器吗?了解如何利用 “kibanaAddFilter” 函数轻松创建动态且响应迅速的 Sankey 可视化。 在这篇博客中,我们将了解如何启用 Vega Sankey 可视…...

styled-components 库的用法介绍和实践总结
styled-components 库的实践用法总结 前言 前段时间开发了一个 NiceTab 浏览器插件,并写了一篇介绍文章,新开发了一款浏览器Tab管理插件,OneTab 的升级替代品, 欢迎品尝!。 在插件中用到了 styled-components 这个库,于是做一个基本的介绍和分享。 在开发 NiceTab 插件…...

SSE(Server-Sent Events)主动推送消息
说明 使用Java开发web应用,大多数时候我们提供的接口返回数据都是一次性完整返回。有些时候,我们也需要提供流式接口持续写出数据,以下提供一种简单的方式。 SSE(Server-Sent Events) SSE 是一种允许服务器单向发送事…...

pandas.core.frame.DataFrame怎么进行对象内容的读写
在 Python 中,pandas.core.frame.DataFrame 是 Pandas 数据库的核心数据结构,可以方便地读取和操作表格数据。以下是几种常见的读取内容的方法: 读取特定列 通过列名获取数据。 # 假设 df 是一个 DataFrame data df["列名"] # …...

短作业优先调度算法
一、实验目的 了解并掌握作业调度的功能,熟悉并掌握各种作业调度算法。 二、实验内容 模拟实现SJF调度。 设置作业体:作业名,作业的到达时间,服务时间,作业状态(W——等待,R——运行,F——完成)…...

SpringBoot 应用并发处理请求数的深入解析
SpringBoot 应用并发处理请求数的深入解析 一、引言 在现代Web开发中,了解一个应用程序可以同时处理多少个并发请求是至关重要的。 对于基于Spring Boot构建的应用程序来说,这个问题的答案并非绝对,而是取决于多个因素,包括但不…...

MetaGPT中的教程助手:TutorialAssistant
1. 提示词 COMMON_PROMPT """ You are now a seasoned technical professional in the field of the internet. We need you to write a technical tutorial with the topic "{topic}". """DIRECTORY_PROMPT (COMMON_PROMPT "…...

介绍一款docker ui 管理工具
http://vm01:18999/main.html 管理员登陆账号 jinghan/123456 ui启动命令所在文件夹目录 /work/docker/docker-ui 参考链接 DockerUI:一款功能强大的中文Docker可视化管理工具_docker ui-CSDN博客...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...
