数据结构 (35)分配类排序
前言
分配类排序是数据结构中的一种重要排序方法,其核心思想是利用分配和收集过程对元素进行排序,而无需比较元素之间的关键字。这种方法突破了基于关键字比较的排序算法的时间下界,可以达到线性时间复杂度O(n)。
一、分配类排序的基本概念
分配类排序主要包括桶排序和基数排序两大类。这两类排序方法都遵循分配和收集的基本操作,但在具体实现上有所不同。
二、桶排序
工作原理:桶排序的工作原理是将数组分到有限数量的桶中,然后对每个桶中的元素进行排序。桶的数量和大小可以根据待排序数据的特点进行调整。
算法步骤:
- 划分桶:根据某种映射函数,将待排序数据的关键字映射到相应的桶中。
- 桶内排序:对每个桶中的元素进行排序,可以使用其他排序算法,如快速排序。
- 合并结果:将各个桶中的有序元素合并,得到最终的有序序列。
时间复杂度和空间复杂度:桶排序的时间复杂度取决于桶的数量和桶内排序算法的效率,通常为O(n*k),其中n为待排序数据的数量,k为桶的数量。空间复杂度为O(n+k),需要额外的空间来存储桶和桶内的元素。
三、基数排序
工作原理:基数排序是一种非比较型整数排序算法,其原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。具体地,基数排序是按照低位先排序,然后收集;再按照高位排序,然后再收集;直到最高位。有时,基数排序也称为桶排序的扩展版本。
算法步骤(以链式基数排序为例):
- 初始化队列:根据待排序数据的位数,创建相应数量的队列。
- 分配过程:根据当前位数的值,将待排序数据分配到相应的队列中。
- 收集过程:按照队列的顺序,将队列中的元素依次收集起来,形成新的待排序数据序列。
- 重复步骤:对新的待排序数据序列重复上述分配和收集过程,直到所有位数都处理完毕。
时间复杂度和空间复杂度:基数排序的时间复杂度为O(n*k),其中n为待排序数据的数量,k为数据的最大位数。空间复杂度为O(n+k),需要额外的空间来存储队列和队列中的元素。
四、分配类排序的特点
- 无需比较:分配类排序不需要比较元素之间的关键字,从而避免了比较操作的开销。
- 线性时间复杂度:在最佳情况下,分配类排序可以达到线性时间复杂度O(n)。
- 适用场景:桶排序适用于数据分布均匀且桶的数量和大小选择合理的情况;基数排序适用于整数排序且数据位数较多的情况。
五、分配类排序的应用
分配类排序在数据处理、数据挖掘、信息检索等领域有着广泛的应用。例如,在搜索引擎中,可以使用桶排序对搜索结果进行分页处理;在图像处理中,可以使用基数排序对像素值进行排序等。
![]() 结语
结语
接纳自己的不完美
学会成长和进步
!!!

相关文章:

数据结构 (35)分配类排序
前言 分配类排序是数据结构中的一种重要排序方法,其核心思想是利用分配和收集过程对元素进行排序,而无需比较元素之间的关键字。这种方法突破了基于关键字比较的排序算法的时间下界,可以达到线性时间复杂度O(n)。 一、分配类排序的基本概念 分…...

Cesium隐藏默认控件
终于有时间开始整理下知识点了。 开搞 本地环境 vue3vitecesiumvite和cesium都是最新版本这里有个问题需要注意,就是如何为Cesium配置Vite,随便检索一下,大部分都时通过插件【vite-plugin-cesium】作为解决方案,我本地创建新的示…...
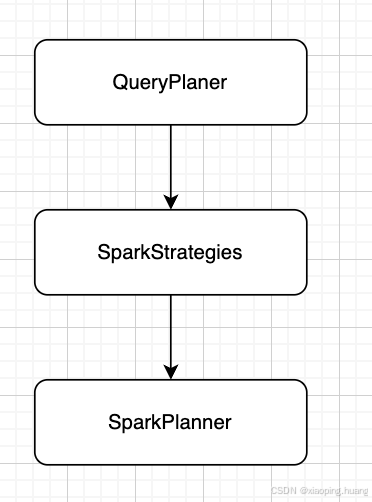
Spark SQL 执行计划解析源码分析
本文用于记录Spark SQL执行计划解析的源码分析。文中仅对关键要点进行提及,无法面面具到,仅描述大体的框架。 Spark的Client有很多种,spark-sql,pyspark,spark- submit,R等各种提交方式,这里以…...

rabbitMq举例
新来个技术总监,把 RabbitMQ 讲的那叫一个透彻,佩服! 生产者 代码举例 public String sendMsg(final String exchangeName,final String routingKey,final String msg) {} /*** 发送消息* param exchangeName exchangeName* param routin…...

奇怪的知识又增加了:ESP32下的Lisp编程=>ULisp--Lisp for microcontrollers
ESP32下有MicroPython,那么我就在想,有Lisp语言支持吗?答案是果然有!有ULisp,专门为MCU设计的Lisp! 网址:uLisp - Lisp for microcontrollers 介绍:用于微控制器的 Lisp 适用于 Ar…...

渗透测试之信息收集
免责声明:使用本教程或工具,用户必须遵守所有适用的法律和法规,并且用户应自行承担所有风险和责任。 文章目录 1. 基础信息收集2. 网络资产发现3. 网站和应用信息4. 技术栈识别5. 安全漏洞和配置6. 移动应用分析7.Google语法常见Google使用场…...

基本分页存储管理
一、实验目的 目的:熟悉并掌握基本分页存储管理的思想及其实现方法,熟悉并掌握基本分页存储管理的分配和回收方式。 任务:模拟实现基本分页存储管理方式下内存空间的分配和回收。 二、实验内容 1、实验内容 内存空间的初始化——可以由用户输…...
SQLServer到MySQL的数据高效迁移方案分享
SQL Server数据集成到MySQL的技术案例分享 在企业级数据管理中,跨平台的数据集成是一个常见且关键的任务。本次我们将探讨如何通过轻易云数据集成平台,将巨益OMS系统中的退款单明细表从SQL Server高效、安全地迁移到MySQL数据库中。具体方案名称为“7--…...

软考:工作后再考的性价比分析
引言 在当今的就业市场中,软考(软件设计师、系统分析师等资格考试)是否值得在校学生花费时间和精力去准备?本文将从多个角度深入分析软考在不同阶段的性价比,帮助大家做出明智的选择。 一、软考的价值与局限性 1.1 …...

shell编程(完结)
shell编程(完结) 声明! 学习视频来自B站up主 泷羽sec 有兴趣的师傅可以关注一下,如涉及侵权马上删除文章 笔记只是方便各位师傅的学习和探讨,文章所提到的网站以及内容,只做学习交流,其…...

UNIX数据恢复—UNIX系统常见故障问题和数据恢复方案
UNIX系统常见故障表现: 1、存储结构出错; 2、数据删除; 3、文件系统格式化; 4、其他原因数据丢失。 UNIX系统常见故障解决方案: 1、检测UNIX系统故障涉及的设备是否存在硬件故障,如果存在硬件故障…...

adb连接逍遥安卓模拟器失败的问题解决方案
1、逍遥安卓模拟器进入系统应用,设置-关于平板电脑-版本号,连续点击3次以上,直到提示进入开发者模式,返回设置界面,进入【开发者选项】-【USB调试】开启,之后重启模拟器再次adb尝试连接。 2、android stud…...

【昇腾】NPU ID:物理ID、逻辑ID、芯片映射关系
起因: https://www.hiascend.com/document/detail/zh/Atlas%20200I%20A2/23.0.0/re/npu/npusmi_013.html npu-smi info -l查询所有NPU设备: [naienotebook-npu-bd130045-55bbffd786-lr6t8 DCNN]$ npu-smi info -lTotal Count : 1NPU…...

Three.js曲线篇 8.管道漫游
目录 创建样条曲线 创建管道 透视相机漫游 完整代码 大家不要被这个“管道漫游”这几个字所蒙骗了,学完后大家就知道这个知识点有多脏了。我也是误入歧途,好奇了一下“管道漫游”。好了,现在就给大家展示一下为啥这个只是点脏了。 我也废话…...

scala基础_数据类型概览
Scala 数据类型 下表列出了 Scala 支持的数据类型: 类型类别数据类型描述Scala标准库中的实际类基本类型Byte8位有符号整数,数值范围为 -128 到 127scala.Byte基本类型Short16位有符号整数,数值范围为 -32768 到 32767scala.Short基本类型I…...

【LeetCode刷题之路】622.设计循环队列
LeetCode刷题记录 🌐 我的博客主页:iiiiiankor🎯 如果你觉得我的内容对你有帮助,不妨点个赞👍、留个评论✍,或者收藏⭐,让我们一起进步!📝 专栏系列:LeetCode…...

暂停一下,给Next.js项目配置一下ESLint(Next+tailwind项目)
前提 之前开自己的GitHub项目,想着不是团队项目,偷懒没有配置eslint,后面发现还是不行。eslint的存在可以帮助我们规范代码格式,同时 ctrl s保存立即调整代码格式是真的很爽。 除此之外,团队使用eslint也是好处颇多…...

Windows系统磁盘与分区之详解(Detailed Explanation of Windows System Disks and Partitions)
Windows系统磁盘与分区知识详解 在日常使用Windows操作系统的过程中,我们常常会接触到磁盘管理,磁盘分区等操作.然而,许多人可能并不完全理解磁盘和分区的运作原理以及如何高效管理它们. 本篇文章将探讨Windows系统中关于磁盘和分区的各种知识,帮助大家更好地理解磁盘以及分区…...

顺序表的使用,对数据的增删改查
主函数: 3.c #include "3.h"//头文件调用 SqlListptr sql_cerate()//创建顺序表函数 {SqlListptr ptr(SqlListptr)malloc(sizeof(SqlList));//在堆区申请连续的空间if(NULLptr){printf("创建失败\n");return NULL;//如果没有申请成功ÿ…...

XDMA与FPGA:高效数据传输的艺术
XDMA与FPGA:高效数据传输的艺术 引言 在现代计算系统中,数据传输的效率直接影响系统的整体性能。特别是在涉及到高速数据处理的领域,如高性能计算(HPC)、实时视频处理和大数据分析等,如何高效地在主机与F…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...
