当前位置：首页 > news >正文

专升本-高数 1

news 2026/2/10 12:33:16

第 0 章，基础知识

一，重要公式

1、完全平方

(a+b)²=a²+2ab+b²

(a-b)²=a²-2ab+b²

2、平方差公式

（a-b）(a+b)=a²-b²

3、立方差公式

a³-b³=(a-b)(a²+ab+b²)

4、立方和公式

a³+b³=(a+b)(a²-ab+b²)

二，基本初等函数

1，幂函数

一元二次函数

2，指数函数

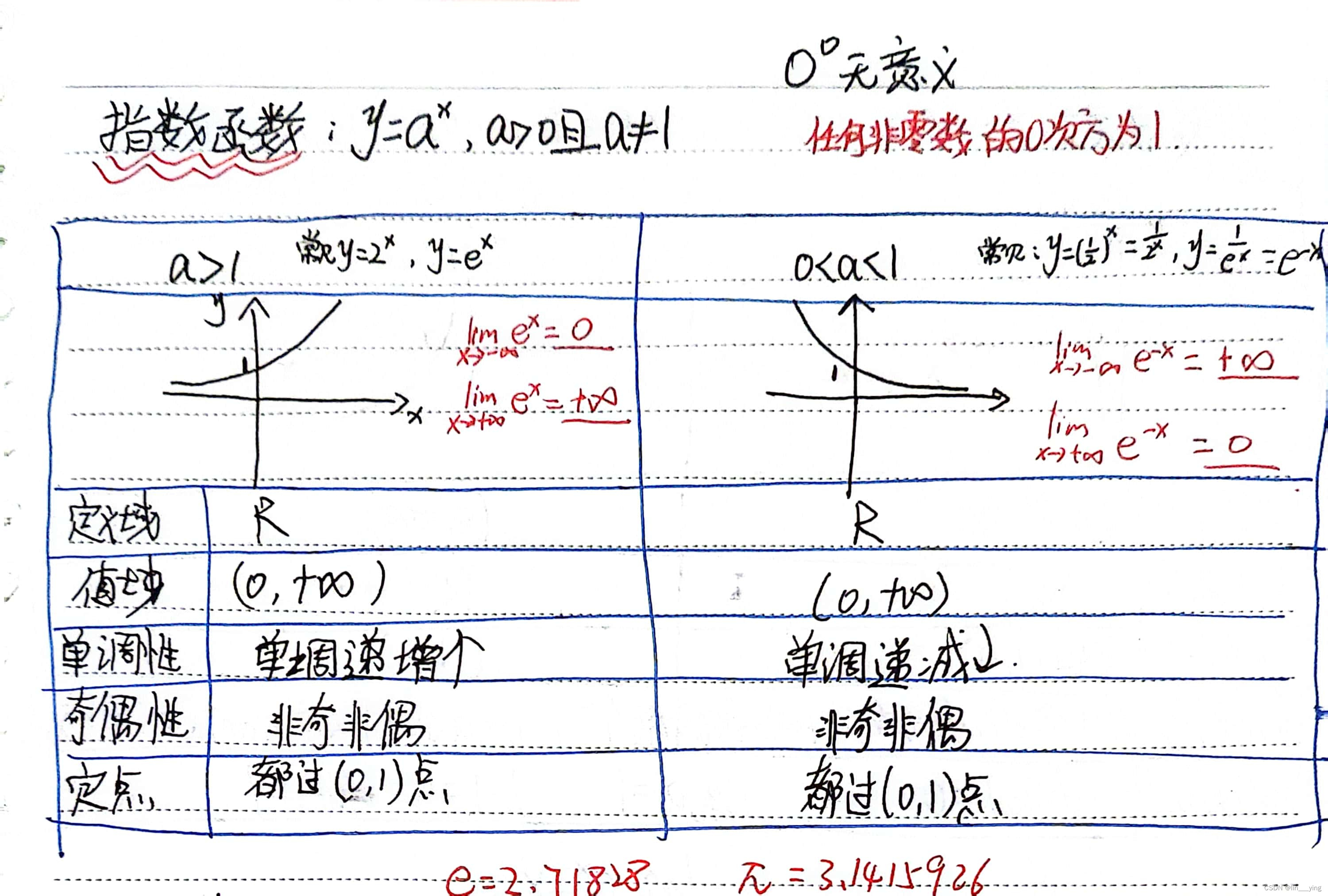
指数运算

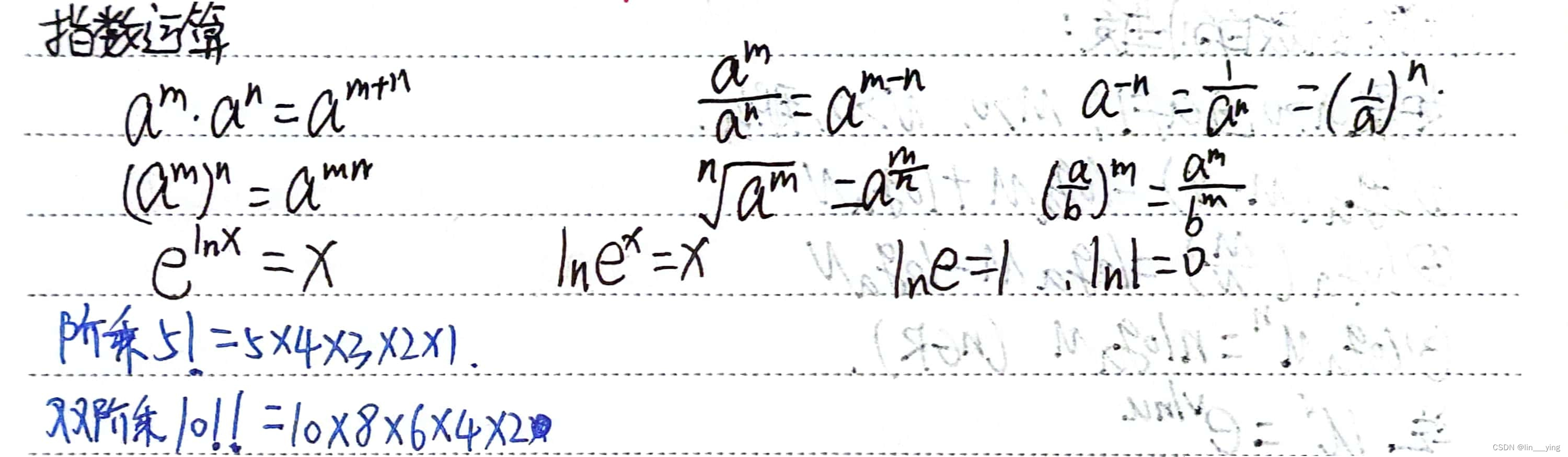
对数运算性质

3，对数函数

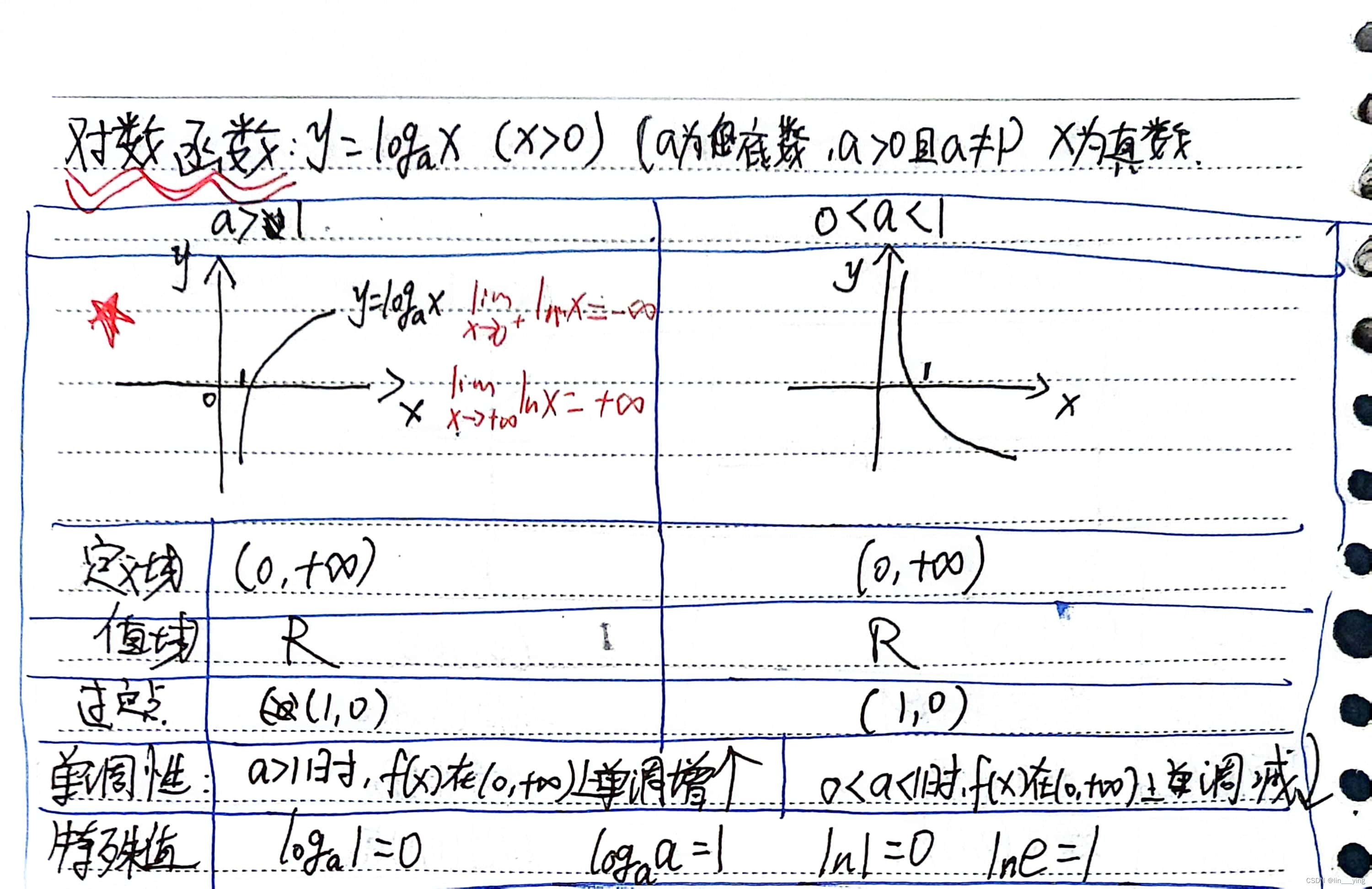
对数函数的性质

4，三角函数

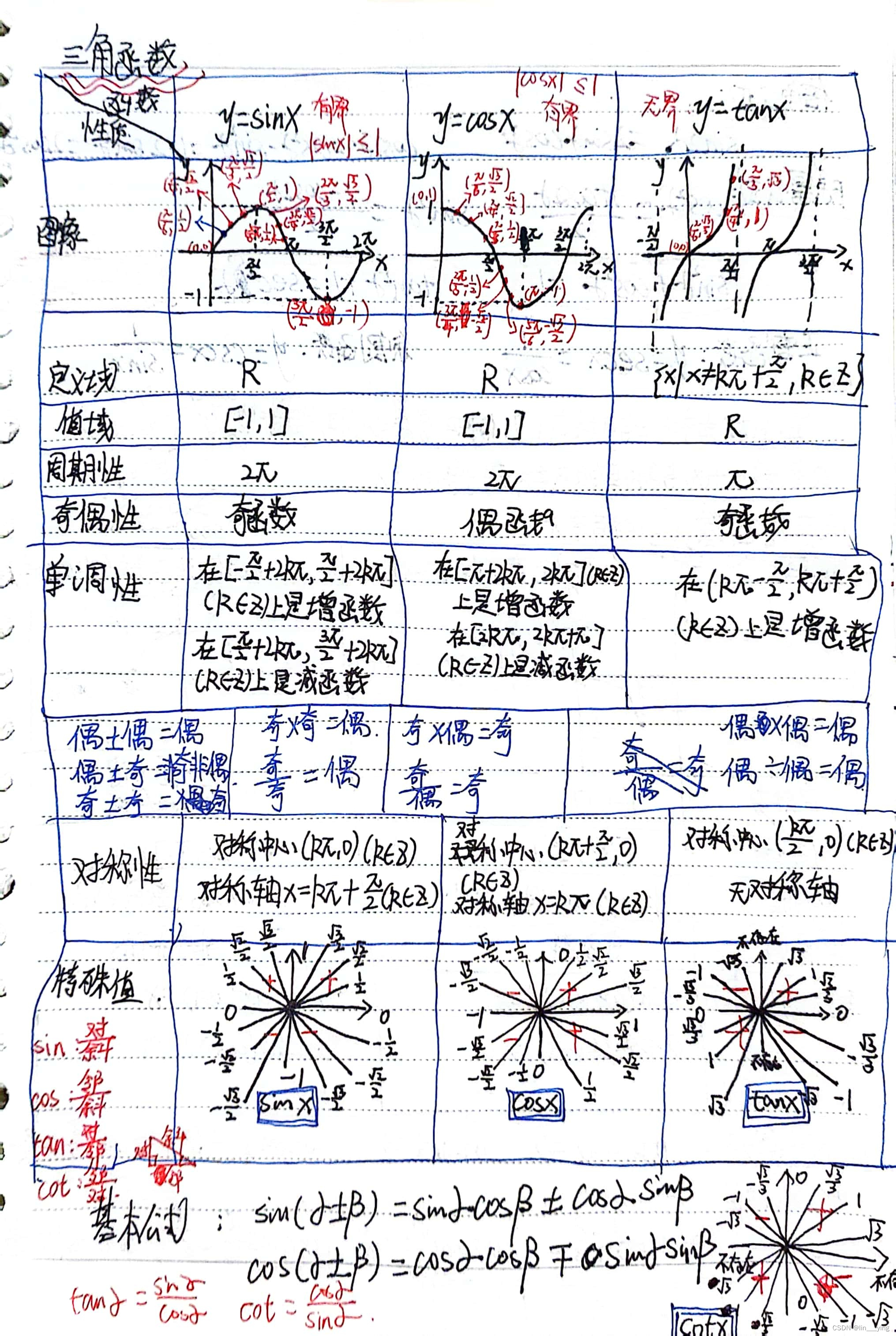
公式

5，反三角函数

三，数列

四，函数

第一章函数极限与连续

一，求函数的定义域

二，奇偶性

三，求函数解析式（表达式）

四，求函数的反函数

五，判断两个函数是否相等

六，集合子集的个数七，无穷小量及阶的比较

八，极限

九，未定式极限

十，连续性

十一，函数间断点及其类型的判别

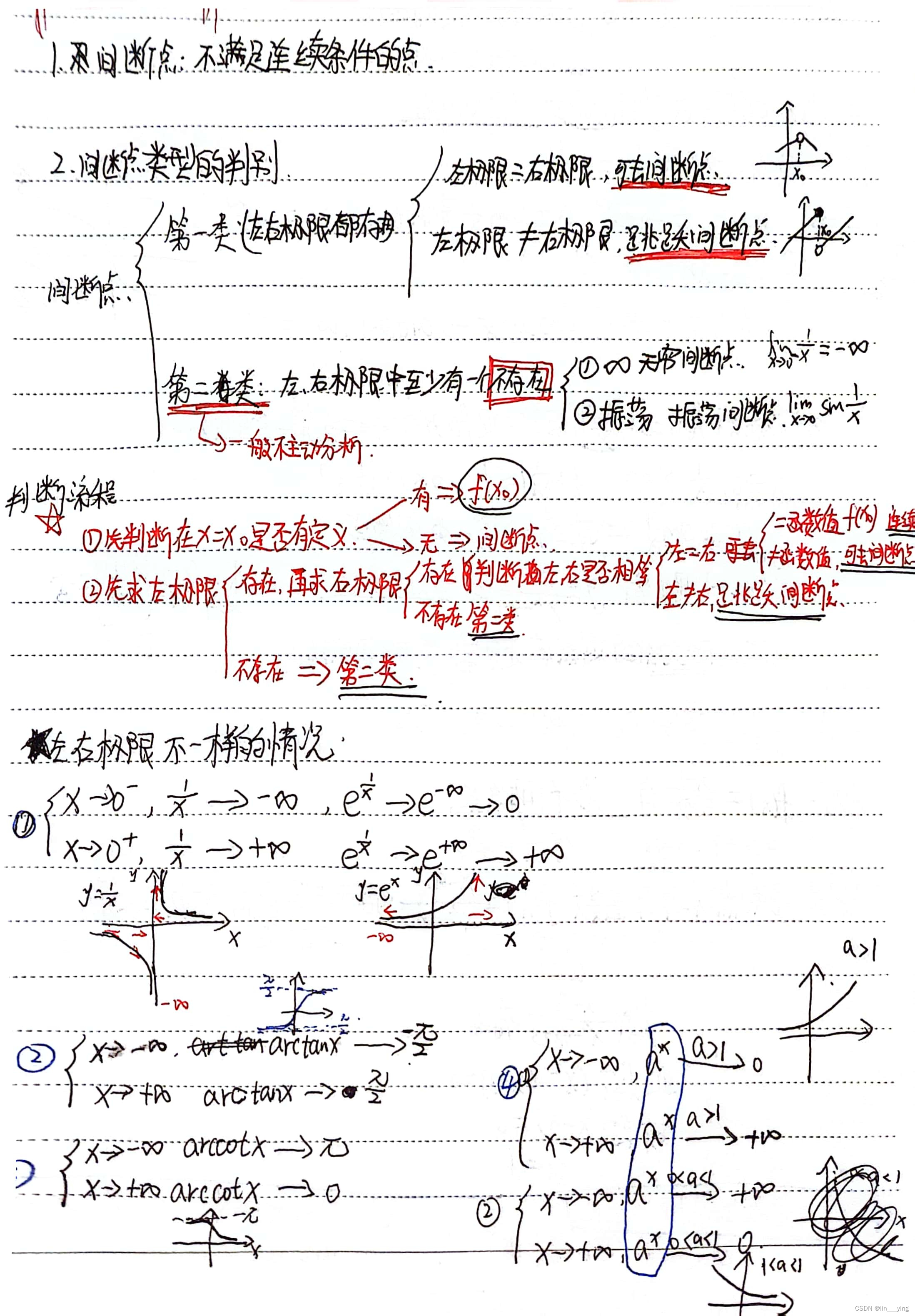
十二，闭区间连续函数的性质

第二章导数与微分

一，导数的定义

二，复合函数求导数

三，高阶导数

四，参数方程求导数

五，隐函数求导数

六，幂函数求导数

七，可导，可微，连续之间的关系

八，导数的几何意义

九，与微分有关的计算

专升本-高数 1

第 0 章，基础知识一，重要公式 1、完全平方 (ab)a2abb (a-b)a-2abb 2、平方差公式 （a-b）(ab)a-b 3、立方差公式 a-b(a-b)(aabb) 4、立方和公式 ab(ab)(a-abb) 二，基本初等函数 1，幂函数一元二…...

编程日记 2024/12/15 1:40:27

【考前预习】3.计算机网络—数据链路层

往期推荐【考前预习】2.计算机网络—物理层-CSDN博客【考前预习】1.计算机网络概述-CSDN博客浅谈云原生--微服务、CICD、Serverless、服务网格_云原生cicd-CSDN博客子网掩码、网络地址、广播地址、子网划分及计算_子网广播地址-CSDN博客浅学React和JSX-CSDN博客目录 1.数…...

编程日记 2024/12/15 1:39:26

DockeUI 弱口令登录漏洞+未授权信息泄露

0x01 产品描述： DockerUI是一款开源的、强大的、轻量级的Docker管理工具。DockerUI覆盖了 docker cli 命令行 95% 以上的命令功能，通过可视化的界面，即使是不熟悉docker命令的用户也可以非常方便的进行Docker和Docker Swarm集群进行管理和维护。0x02 漏洞描述： DockerUI中存…...

编程日记 2024/12/15 1:38:25

【电子元器件】电感基础知识

本文章是笔者整理的备忘笔记。希望在帮助自己温习避免遗忘的同时，也能帮助其他需要参考的朋友。如有谬误，欢迎大家进行指正。一、电感的基本工作原理 1. 电感的基本工作原理如下： （1） 当线圈中有电流通过时&#…...

编程日记 2024/12/15 1:37:24

【SSH+X11】VsCode使用Remote-SSH在远程服务器的docker中打开Rviz

🚀今天来分享一下通过VsCode的Remote-SSH插件在远程服务器的docker中打开Rviz进行可视化的方法。具体流程如下图所示，在操作开始前，请先重启设备，排除之前运行配置的影响： ⭐️ 我这里是使用主机连接服务器&#xff…...

编程日记 2024/12/15 1:36:22

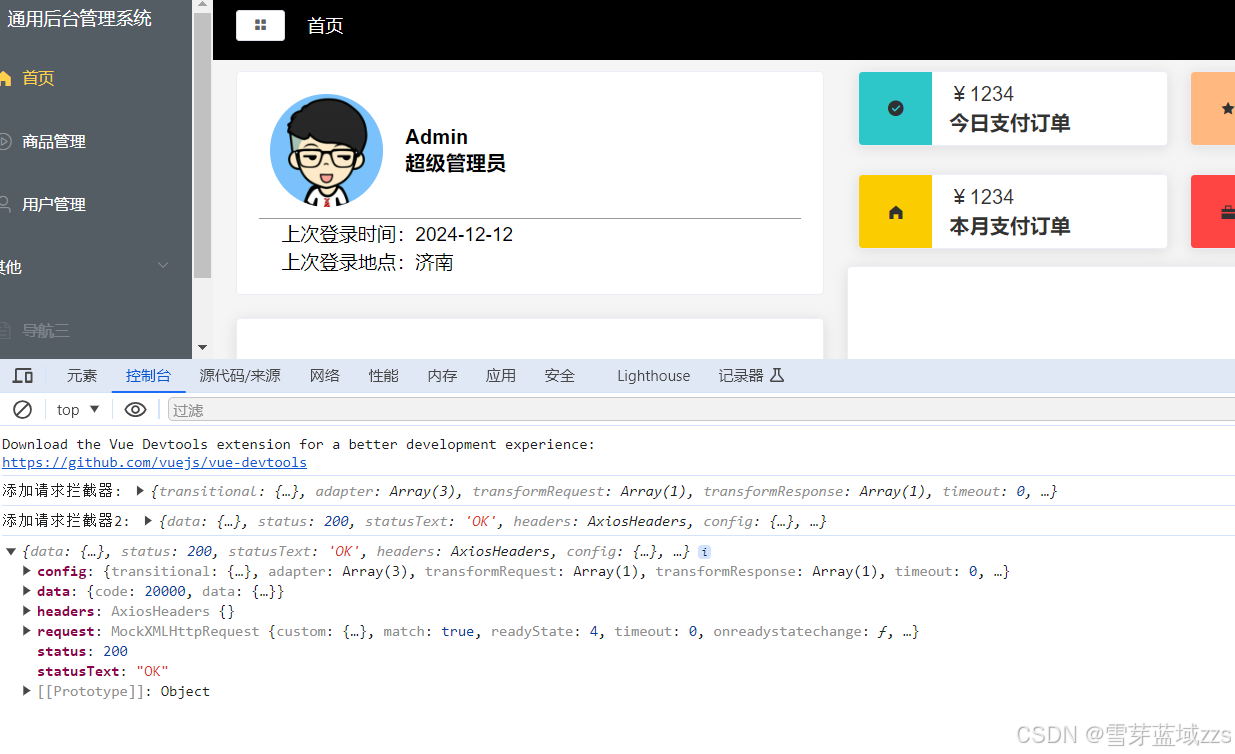
Vue Web开发（五）

1. axios axios官方文档异步库axios和mockjs模拟后端数据，axios是一个基于promise的HTTP库，使用npm i axios。在main.js中引入，需要绑定在Vue的prototype属性上，并重命名。 （1）main.js文件引用 imp…...

编程日记 2024/12/15 1:35:21

HarmonyOS：使用Grid构建网格

一、概述网格布局是由“行”和“列”分割的单元格所组成，通过指定“项目”所在的单元格做出各种各样的布局。网格布局具有较强的页面均分能力，子组件占比控制能力，是一种重要自适应布局，其使用场景有九宫格图片展示、日历、计算器…...

编程日记 2024/12/15 1:34:19

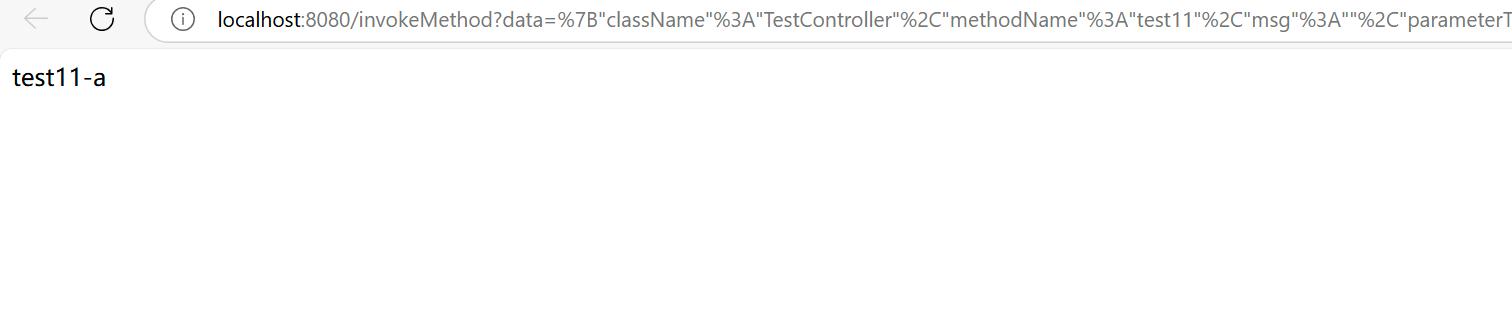
开源Java快速自测工具，可以调用系统内任意一个方法

java快速测试框架，可以调到系统内任意一个方法，告别写单测和controller的困扰。开源地址：https://gitee.com/missyouch/Easy-JTest 我们在开发时很多时候想要测试下自己的代码，特别是service层或者是更底层的代码，就…...

编程日记 2024/12/15 1:33:18

力扣刷题TOP101: 29.BM36 判断是不是平衡二叉树

目录： 目的思路复杂度记忆秘诀 python代码目的： 输入一棵节点数为 n 二叉树，判断该二叉树是否是平衡二叉树。思路什么是平衡二叉树（AVL 树）？ 每个节点的左子树和右子树的高度差不能超过 1。确保…...

编程日记 2024/12/15 1:32:17

【在Linux世界中追寻伟大的One Piece】自旋锁

目录 1 -> 概述 2 -> 原理 3 -> 优缺点及使用场景 3.1 -> 优点 3.2 -> 缺点 3.3 -> 使用场景 4 -> 纯软件自旋锁类似的原理实现 4.1 -> 结论 5 -> 样例代码 1 -> 概述自旋锁是一种多线程同步机制，用于保护共享资源避免受并…...

编程日记 2024/12/15 1:31:16

前端编辑器JSON HTML等，vue2-ace-editor，vue3-ace-editor

与框架无关 vue2-ace-editor有问题，ace拿不到（brace） 一些组件都是基于ace-builds或者brace包装的不如直接用下面的，不如直接使用下面的 <template><div ref"editor" class"json-editor"><…...

编程日记 2024/12/15 1:27:12

C++ 中的运算符重载

运算符重载是C中的一种特性，它允许开发者为自定义类型定义或改变标准运算符的行为。通过运算符重载，你可以使得用户定义的类像内置类型一样使用运算符，比如加法、减法、赋值等。如何在C中进行运算符重载？ 重载运算符的语法&#…...

编程日记 2024/12/15 1:19:05

渗透测试工具 -- SQLmap安装教程及使用

随着网络安全问题日益严峻，渗透测试成为了保护信息安全的重要手段。而在渗透测试的众多工具中，SQLmap凭借其强大的自动化SQL注入检测和利用能力，成为了网络安全专家必备的利器。那么，你知道如何高效地使用SQLmap进行漏洞扫描吗&am…...

编程日记 2024/12/15 1:17:02

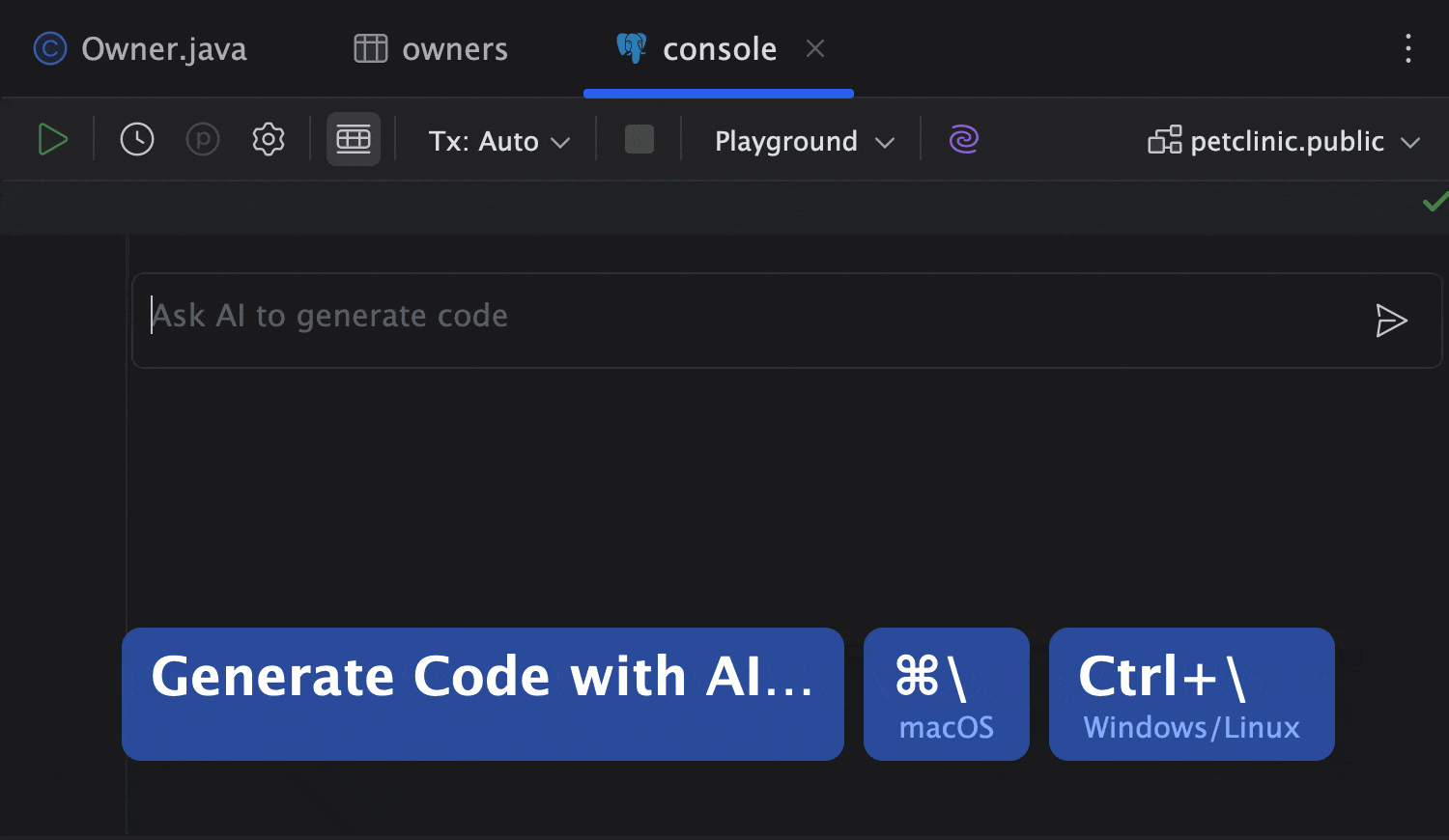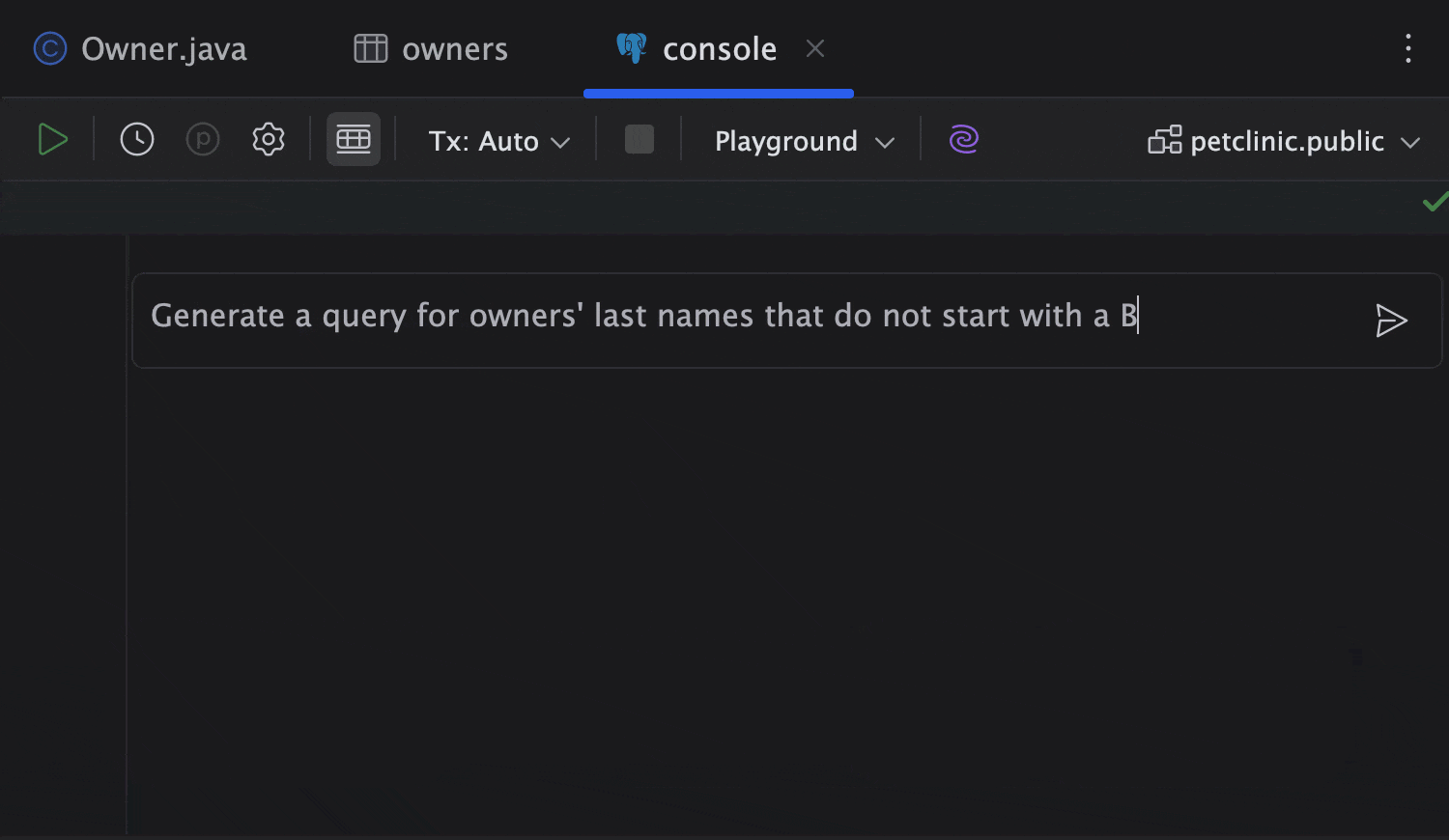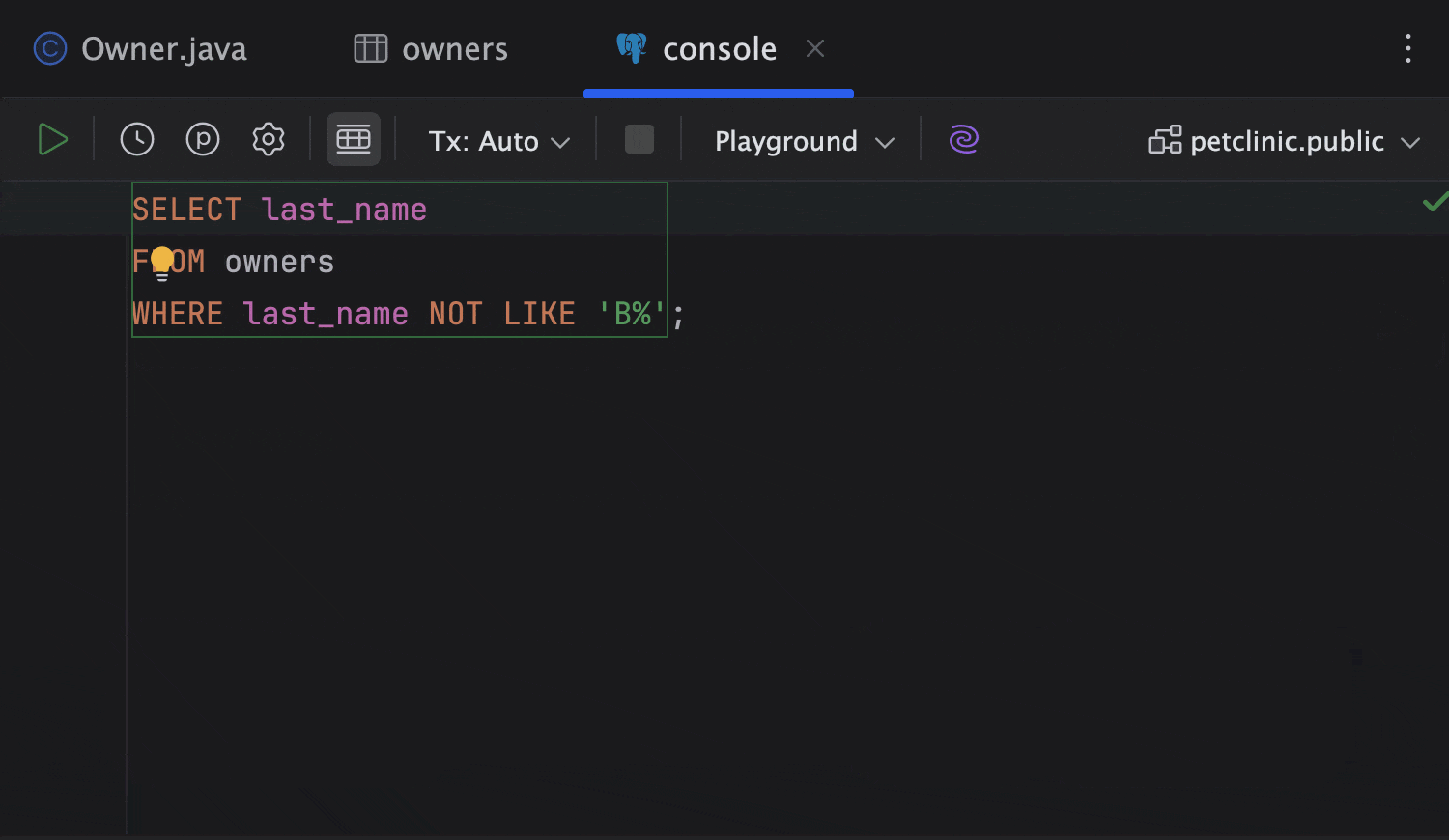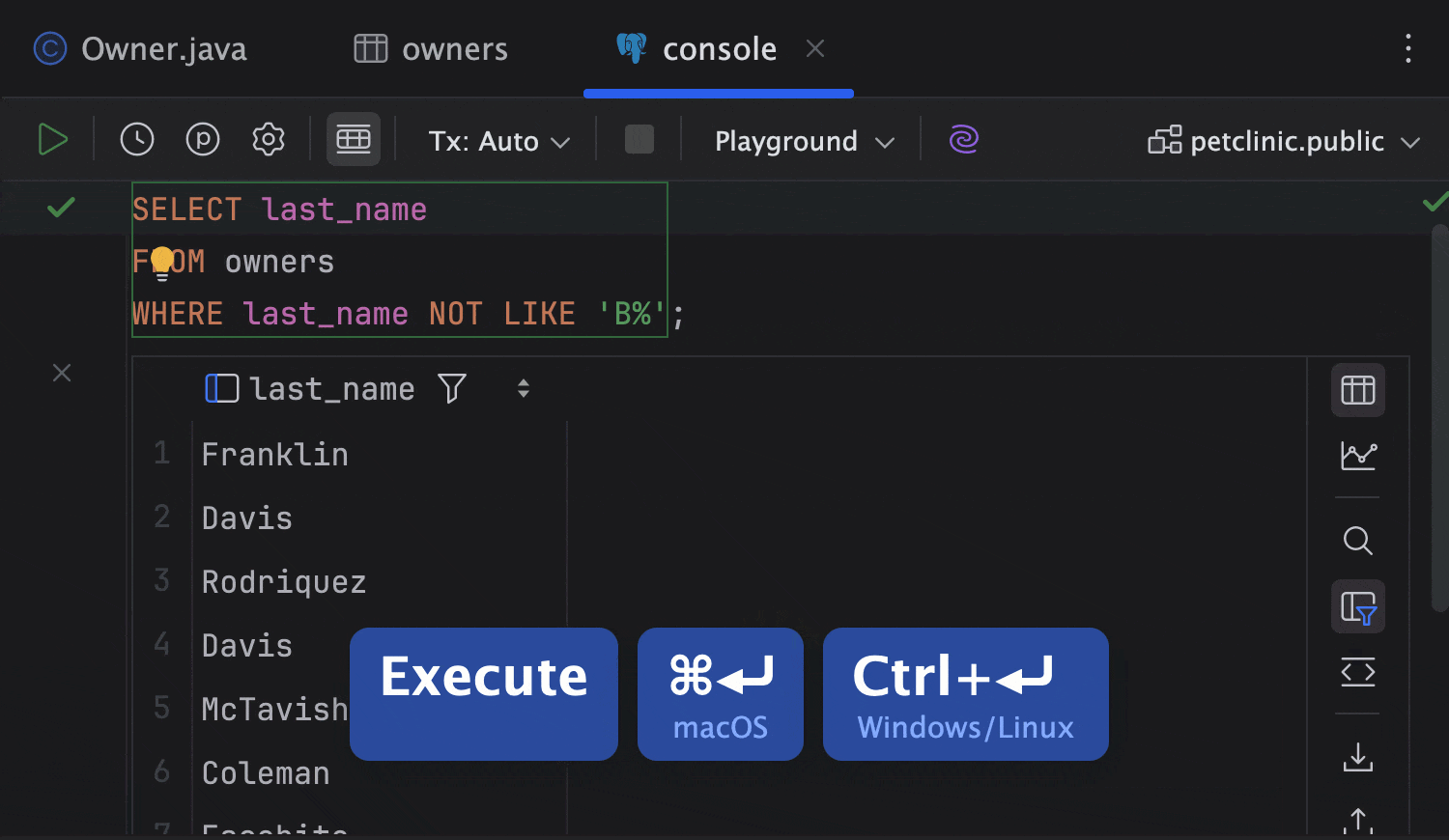
使用 Database Tools 实现高效数据查询的十大 IntelliJ IDEA 快捷键

得益于 IntelliJ IDEA Ultimate 的 Database Tools（数据库工具）中的专用 SQL 查询控制台，您无需离开 IDE 即可轻松修改连接到您的 Java 应用程序的任何数据库中的数据，以及从这些数据库中提取数据。查询控制台具有 SQL 语句特定的…...

编程日记 2024/12/15 1:16:01

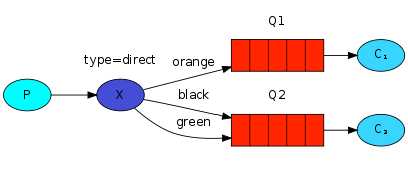
SpringBoot 整合 RabbitMQ 实现流量消峰

RabbitMQ 即一个消息队列，主要是用来实现应用程序的异步和解耦，同时也能起到消息缓冲，消息分发的作用。消息中间件在互联网公司的使用中越来越多，刚才还看到新闻阿里将 RocketMQ 捐献给了 Apache，当然了今天的主角还…...

编程日记 2024/12/15 1:13:59

大数据挖掘建模平台案例分享

大数据挖掘建模平台是由泰迪自主研发，面向企业级用户的大数据挖掘建模平台。平台采用可视化操作方式，通过丰富内置算法，帮助用户快速、一站式地进行数据分析及挖掘建模，可应用于处理海量数据、高复杂性的数据挖掘任务，…...

编程日记 2024/12/15 1:11:56

MySQL数据表的管理

1.创建表语法： create table 表名( 字段名字段里保存数据的类型【(数据的长度) 约束】, 字段名字段里保存数据的类型【(数据的长度) 约束】, 字段名字段里保存数据的类型【(数据的长度) 约束】 ...... ); 注意：数据类型和约束，接下来用…...

编程日记 2024/12/15 1:08:53

SpringBoot【十三(实战篇)】集成在线接口文档Swagger2

一、前言🔥 环境说明：Windows10 Idea2021.3.2 Jdk1.8 SpringBoot 2.3.1.RELEASE 二、如何生成Swagger文档上一期我们已经能正常访问swagger在线文档，但是文档空空如也，对不对，接下来我就教大家怎么把相关的接口都给…...

编程日记 2024/12/15 1:07:52

【C++初阶】第8课—标准模板库STL(string_2)

文章目录 1. string类对象遍历操作1.1 标准库中的成员函数begin( )和end( )1.2 标准库中的成员函数rbegin( )和rend( )1.3 C11引入的4个标准库中的成员函数 2. string类对象的访问2.1 operator[ ]运算符重载访问字符串字符2.2 公有成员函数at访问字符2.3 公有成员函数back()和f…...

编程日记 2024/12/15 1:06:50

【arm】程序跑飞，SWD端口不可用修复(N32G435CBL7)

项目场景： 国民N32G43X系列，烧录了一个测试程序，在DEBUG中不知什么原因挂掉，然后就无法连接SWD或JLINK。问题描述在SWD配置中不可见芯片型号，无法connect，无法烧录。但基本判断是芯片没有损坏。怀疑是程…...

编程日记 2024/12/15 1:03:47

浏览器访问 AWS ECS 上部署的 Docker 容器（监听 80 端口）

✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义（Task Definition&…...

编程新知 2026/2/8 15:03:14

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造，完美适配AGV和无人叉车。同时，集成以太网与语音合成技术，为各类高级系统（如MES、调度系统、库位管理、立库等）提供高效便捷的语音交互体验。 L…...

编程新知 2026/2/8 4:23:14

大话软工笔记—需求分析概述

需求分析，就是要对需求调研收集到的资料信息逐个地进行拆分、研究，从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。需求分析的作用非常重要，后续设计的依据主要来自于需求分析的成果，包括: 项目的目的…...

编程新知 2026/1/28 10:58:50

渗透实战PortSwigger靶场-XSS Lab 14：大多数标签和属性被阻止

编程新知 2026/1/24 13:05:24

关于 WASM：1. WASM 基础原理

一、WASM 简介 1.1 WebAssembly 是什么？ WebAssembly（WASM） 是一种能在现代浏览器中高效运行的二进制指令格式，它不是传统的编程语言，而是一种低级字节码格式，可由高级语言（如 C、C、Rust&am…...

编程新知 2025/11/19 10:53:07

汇编常见指令

汇编常见指令一、数据传送指令指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX（不访问内存）XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

编程新知 2026/1/23 2:04:44

select、poll、epoll 与 Reactor 模式

在高并发网络编程领域，高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表，以及基于它们实现的 Reactor 模式，为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。一、I…...

编程新知 2026/2/10 11:29:59

【LeetCode】3309. 连接二进制表示可形成的最大数值（递归|回溯|位运算）

LeetCode 3309. 连接二进制表示可形成的最大数值（中等） 题目描述解题思路Java代码题目描述题目链接：LeetCode 3309. 连接二进制表示可形成的最大数值（中等） 给你一个长度为 3 的整数数组 nums。现以某种顺序连接…...

编程新知 2025/7/5 18:01:05

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)

目录一、SQL注入二、字符型SQL注入三、字符型注入与数字型注入四、源码分析五、渗透实战 1、渗透准备 2、SQL注入探测 （1）输入单引号 （2）万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

编程新知 2026/2/5 5:47:53

针对药品仓库的效期管理问题，如何利用WMS系统“破局”

案例： 某医药分销企业，主要经营各类药品的批发与零售。由于药品的特殊性，效期管理至关重要，但该企业一直面临效期问题的困扰。在未使用WMS系统之前，其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...

编程新知 2026/2/5 14:06:00