前缀和与差分算法详解
定义
前缀和是一种数据预处理技术,它指的是从数组的第一个元素开始,到当前元素为止的所有元素的和。这种技术可以快速计算任意区间内元素的和,而不需要每次都从头开始累加。
差分则是前缀和的逆运算,它主要用于处理对数组某个区间内所有元素同时增加或减少一个常数的操作。
一维前缀和
对于数组a,其前缀和数组s可以表示为s[i] = a[1] + a[2] + ... + a[i]。
在一维数组中,前缀和可以在O(1)的时间复杂度内求出任意区间[l, r]的和,公式为a[l] + a[l+1] + ... + a[r] = s[r] - s[l-1]。
下面用一个具体的题目来说明:
输入一个长度为n的整数序列。接下来再输入m个询问,每个询问输入一对l, r。对于每个询问,输出原序列中从第l个数到第r个数的和。
输入格式
第一行包含两个整数n和m。
第二行包含n个整数,表示整数数列。
接下来m行,每行包含两个整数l和r,表示一个询问的区间范围。
输出格式
共m行,每行输出一个询问的结果。
数据范围
1≤l≤r≤n,
1≤n,m≤100000,
−1000≤数列中元素的值≤1000
输入样例
5 3
2 1 3 6 4
1 2
1 3
2 4
输出样例
3
6
10
代码实现:
#include <iostream>using namespace std;int main()
{int n, m;cin >> n >> m;int *num = new int[n + 1]; // 用于存储所给数列int *sum = new int[n + 1]; // sum[i]存储num[]中前i项和,这样闭区间[l,r]上的数列和就可表示为sum[r]-sum[l-1],时间复杂度为O(1),比从l到r的累加快for (int i = 1; i <= n; i++)cin >> num[i];for (int i = 1; i <= n; i++)sum[i] = sum[i - 1] + num[i]; // 计算前i项和并存储while (m--){int l, r;cin >> l >> r;cout << sum[r] - sum[l - 1] << endl;}return 0;
}
一维差分
差分是前缀和的逆运算。对于前缀和数组来说,原数组就是差分数组。理解差分算法首先需要知道怎么求差分数组。由于前缀和数组表示从第一个元素到当前元素的和,所以当给定前缀和数组的时候,我们通过相邻两项做差就能得到差分数组。
差分数组是根基,前缀和数组是受差分数组影响的。当差分数组的某一项加上了x,前缀和数组中这一项及其后面所有项在求和时都会受到影响,也都增加了x。减法同理。
根据这个性质,我们就可以快速的进行区间更新操作。具体做法是将需要进行区间更新的数组视为前缀和数组,然后将区间更新转化为对差分数组的操作。例如,我们需要将a数组的[l, r]范围的数都加上x。我们先计算a数组对应的差分数组b。然后我们将b[l]加上x,这就相当于前缀和数组a中第l项及其后面所有项也都加上了x。但是我们要更新的是[l, r],第r项后面多更新了,所以需要进行补偿,将b[r + 1]减去x即可。想要得到更新后的数组,将差分数组再转化为前缀和数组即可。
下面用一个具体的题目来说明:
输入一个长度为n的整数序列。接下来输入m个操作,每个操作包含三个整数l, r, c,表示将序列中[l, r]之间的每个数加上c。请你输出进行完所有操作后的序列。
输入格式
第一行包含两个整数n和m。
第二行包含n个整数,表示整数序列。
接下来m行,每行包含三个整数l,r,c,表示一个操作。
输出格式
共一行,包含n个整数,表示最终序列。
数据范围
1≤n,m≤100000,
1≤l≤r≤n,
−1000≤c≤1000,
−1000≤整数序列中元素的值≤1000
输入样例
6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1
输出样例
3 4 5 3 4 2
代码实现:
#include <iostream>using namespace std;const int N = 100000;
int a[N] = {}, b[N] = {}; // a数组为前缀和数组,b数组为差分数组int main()
{int n, m;cin >> n >> m;for (int i = 1; i <= n; i++){cin >> a[i]; // 将所给数列填入前缀和数组ab[i] = a[i] - a[i - 1]; // 同时利用相邻两项做差计算出差分数组b}while (m--){int l, r, c;cin >> l >> r >> c;b[l] += c; // 差分数组在第l项加了c导致从第l项开始后面的前缀和数组每项也都加了cb[r + 1] -= c; // 差分数组在第r+1项减c会让前缀和数组从第r+1项开始少了c,正好和前面加的c抵消,实现[l,r]闭区间上a数组都加了c}for (int i = 1; i <= n; i++){b[i] += b[i - 1]; // 求前i项和,并保存在b数组的第i项,即将b数组重构成新的前缀和数组cout << b[i] << " ";}return 0;
}
二维前缀和
输入一个n行m列的整数矩阵,再输入q个询问,每个询问包含四个整数x1, y1, x2, y2,表示一个子矩阵的左上角坐标和右下角坐标。对于每个询问输出子矩阵中所有数的和。
输入格式
第一行包含三个整数n,m,q。
接下来n行,每行包含m个整数,表示整数矩阵。
接下来q行,每行包含四个整数x1, y1, x2, y2,表示一组询问。
输出格式
共q行,每行输出一个询问的结果。
数据范围
1≤n,m≤1000,
1≤q≤200000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤矩阵内元素的值≤1000
输入样例
3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4
输出样例
17
27
21
代码实现
#include <iostream>using namespace std;const int N = 1001;
int a[N][N], s[N][N]; // a数组用于存放所给矩阵
// s数组存放以a[1][1]为左上角,a[i][j]为右下角的矩阵和int main()
{int n, m, q;cin >> n >> m >> q;for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)cin >> a[i][j]; // 输入a数组for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];// s[i-1][j]+s[i][j-1]有一块重叠区域被算了两遍,即s[i-1][j-1],所以减去s[i-1][j-1],// 再加上缺少的那一个格子,a[i][j]即为s[i][j]while (q--){int x1, x2, y1, y2;cin >> x1 >> y1 >> x2 >> y2;cout << s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1] << endl;// 类比概率论中二维随机变量的概率分布}return 0;
}二维差分
输入一个n行m列的整数矩阵,再输入q个操作,每个操作包含五个整数x1, y1, x2, y2, c,其中(x1, y1)和(x2, y2)表示一个子矩阵的左上角坐标和右下角坐标。每个操作都要将选中的子矩阵中的每个元素的值加上c。请你将进行完所有操作后的矩阵输出。
输入格式
第一行包含整数n,m,q。
接下来n行,每行包含m个整数,表示整数矩阵。
接下来q行,每行包含5个整数x1, y1, x2, y2, c,表示一个操作。
输出格式
共 n 行,每行 m 个整数,表示所有操作进行完毕后的最终矩阵。
数据范围
1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤c≤1000,
−1000≤矩阵内元素的值≤1000
输入样例
3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1
输出样例
2 3 4 1
4 3 4 1
2 2 2 2
代码实现
#include <iostream>using namespace std;const int N = 1001;
int a[N][N] = {}, b[N][N] = {}; // a数组为前缀和数组,b数组为差分数组int main()
{int n, m, q;cin >> n >> m >> q;for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)cin >> a[i][j]; // 输入到a数组for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)b[i][j] = a[i][j] - a[i][j - 1] - a[i - 1][j] + a[i - 1][j - 1]; // 构建差分数组// 也是类比概率论中二维随机变量的概率分布while (q--){int x1, x2, y1, y2, c;cin >> x1 >> y1 >> x2 >> y2 >> c;b[x1][y1] += c; // 此行使以(x1,y1)为左上角,右下角无限延伸的区域的前缀和数组都加上了cb[x2 + 1][y1] -= c; // 此行使以(x2+1,y1)为左上角,右下角无限延伸的区域的前缀和数组都减去了c,越来越接近目标区域了b[x1][y2 + 1] -= c; // 此行使以(x1,y2+1)为左上角,右下角无限延伸的区域的前缀和数组都减去了c,目标区域多减了以(x2+1,y2+1)为左上角,右下角无限延伸的区域b[x2 + 1][y2 + 1] += c; // 补上多减的那一块}for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1]; // 求以(1,1)为左上角(i,j)为右下角的区域的和并保存在b[i][j],即将b数组重构成前缀和数组for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++)cout << b[i][j] << " "; // 输出cout << endl;}return 0;
}相关文章:

前缀和与差分算法详解
定义 前缀和是一种数据预处理技术,它指的是从数组的第一个元素开始,到当前元素为止的所有元素的和。这种技术可以快速计算任意区间内元素的和,而不需要每次都从头开始累加。 差分则是前缀和的逆运算,它主要用于处理对数组某个区…...

《深入探究:C++ 在多方面对 C 语言实现的优化》
目录 一、C 在 C 上进行的优化二、C 关键字(C 98)三、C 的输入输出1. cin 和 cout 的使用2. cin、cout 和 scanf()、printf() 的区别 三、命名空间1. 命名空间的使用2. 嵌套命名空间3. 在多个头文件中使用相同的命名空间 四、函数缺省值1. 缺省值的使用2…...

React 第十六节 useCallback 使用详解注意事项
useCallback 概述 1、useCallback 是在React 中多次渲染缓存函数的 Hook,返回一个函数的 memoized的值; 2、如果多次传入的依赖项不变,那么多次定义的时候,返回的值是相同的,防止频繁触发更新; 3、多应用在 父组件为函…...

使用C#和OPenCV实现圆形检测
文章目录 霍夫变换使用 OpenCV 和 C# 实现圆形检测 霍夫变换 在计算机视觉中,圆形检测是一个常见且有用的任务,特别是在物体识别、图像分析和图形处理等领域。OpenCV 是一个强大的开源计算机视觉库,它提供了许多工具来实现不同的图像处理功能…...

评估一套呼叫中心大模型呼入机器人的投入回报比?
评估一套呼叫中心大模型呼入机器人的投入回报比? 原作者:开源呼叫中心FreeIPCC,其Github:https://github.com/lihaiya/freeipcc 评估一套呼叫中心大模型呼入机器人的投入回报比(ROI),是一个多…...

十八、Label 和 Selector
Label 是键值对,用来标识 Kubernetes 资源(如 Pod、Node、Service 等)的属性。它们并不直接影响资源的行为,但可以帮助用户快速组织、查询和操作这些资源。标签可以用于选择、过滤和分组。 Label: 标签对 k8s 中各种资源进行分类、分组,如Pod和节点进行分组。通过添加kev…...

实现按键按下(低电平)检测到下降沿
按照流程进行编程 步骤1: 初始化函数 包括时基工作参数配置 输入通道配置 更新中断使能 使能捕获、捕获中断及计数器 HAL_TIM_IC_Init(&ic_handle) //时基参数配置 HAL_TIM_IC_ConfigChannel(&ic_handle,&ic_config,TIM_CHANNEL_2) //输…...

解析 SSM 垃圾分类系统,助力生态平衡
前 言 垃圾分类系统,传统的垃圾分类系统模式还处于线下管理阶段,管理效率极低。随着垃圾分类系统信息的不断增多,传统基于线下管理模式已经无法满足当前用户需求,随着信息化时代的到来。通过该系统的设计,管理员可以管…...

软件工程 设计的复杂性
复杂性代表事件或事物的状态,它们具有多个相互关联的链接和高度复杂的结构。在软件编程中,随着软件设计的实现,元素的数量以及它们之间的相互联系逐渐变得庞大,一下子变得难以理解。 如果不使用复杂性指标和度量,软件…...

Nginx 限制只能白名单 uri 请求的配置
实际生产项目中,大多数时候我们会将后端的 http 接口通过前置 nginx 进行反向代理,对互联网用户提供服务。往往我们后端服务所能提供的接口服务是大于互联网用户侧的实际请求的接口地址数量的(例如后端服务一共有100个api接口,经过…...

QT c++ 同时使用sqlite 和mysql数据库的问题
在项目开发中,同时使用了sqlite 和mysql数据库,分开这两部分运行功能都正常,但是一起运行,就异常,sqlite部分不能使用。 现象:出现如下提示 QSqlDatabasePrivate::addDatabase: duplicate connection nam…...

redis集群 服务器更换ip,怎么办,怎么更换redis集群的ip
redis集群 服务器更换ip,怎么办,怎么更换redis集群的ip 1、安装redis三主三从集群2、正常状态的redis集群3、更改redis集群服务器的ip 重启服务器 集群会down4、更改redis集群服务器的ip 重启服务器 集群down的原因5、更改redis集群服务器的ip后…...

【C++习题】19.数组中第K个大的元素
题目:数组中第K个大的元素 链接🔗:数组中第K个大的元素 题目: 代码: class Solution { public:int findKthLargest(vector<int>& nums, int k) {// 将数组中的元素先放入优先级队列中priority_queue<i…...

JIS-CTF: VulnUpload靶场渗透
JIS-CTF: VulnUpload来自 <https://www.vulnhub.com/entry/jis-ctf-vulnupload,228/> 1,将两台虚拟机网络连接都改为NAT模式 2,攻击机上做namp局域网扫描发现靶机 nmap -sn 192.168.23.0/24 靶机IP地址192.168.23.162,攻击机IP地址192.168.23.140…...

BGP-面试
简单介绍一下BGP BGP,边界网关协议,属于路径矢量路由协议。属于触发式更新或者增量更新。具有丰富的路由策略,能够灵活的进行路由选择。重心不是在路由学习,而是路由优选、更高效的传递路由和维护大量的路由信息。基于TCP…...

Git-安装与常用命令
目录 1.Git环境配置 1.1下载 1.2配置 1.2.1基本配置 1.2.2常用指令配置别名 1.2.3获取本地仓库 git命令在git bash中演示,会用到一些Linux命令。 1.Git环境配置 1.1下载 Git下载地址:https://git-scm.com/download 傻瓜式安装就可以了。 安装…...

回归预测 | Matlab实现基于BiLSTM-Adaboost双向长短期记忆神经网络结合Adaboost集成学习回归预测
目录 效果一览基本介绍模型设计程序设计参考资料效果一览 基本介绍 回归预测 | Matlab实现基于BiLSTM-Adaboost双向长短期记忆神经网络结合Adaboost集成学习回归预测 模型设计 基于BiLSTM-Adaboost的回归预测模型结合了双向长短期记忆神经网络(BiLSTM)和Adaboost集成学习的…...

微信小程序跳转其他小程序以及跳转网站
一、跳转其他小程序 1.1 知道appid和页面路径 wx.navigateToMiniProgram({appId: appid, // 替换为目标小程序 AppIDpath: pathWithParams, // 小程序路径envVersion: release, // 开发版、体验版或正式版success(res) {console.log("跳转到其他小程序成功!&q…...

Not using native diff for overlay2, this may cause degraded performance……
问题现象 案例:Anolis 8.9(4.19.91-26.an8.x86_64) Overlay2存储驱动程序) 当我们安装好Docker之后,通过systemctl status docker -l 会发现有一个告警信息:levelwarning msg"Not using native dif…...

【自用】管材流转项目 数据库恢复之 PIPE 表 二维码相关 各个表恢复 SQL
总览 1.后端前端和数据库 PIPE 页面的关系 2.后端批量生成二维码 jpg 图片 3.为了保证 PIPE 正常使用的调整 4.TRANSFORM(流转表) 一、后端前端和数据库 PIPE 页面的关系 1.前端 关于PIPE页面,首先,在前端,我们已经…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...

el-amap-bezier-curve运用及线弧度设置
文章目录 简介示例线弧度属性主要弧度相关属性其他相关样式属性完整示例链接简介 el-amap-bezier-curve 是 Vue-Amap 组件库中的一个组件,用于在 高德地图 上绘制贝塞尔曲线。 基本用法属性path定义曲线的路径,可以是多个弧线段的组合。stroke-weight线条的宽度。stroke…...
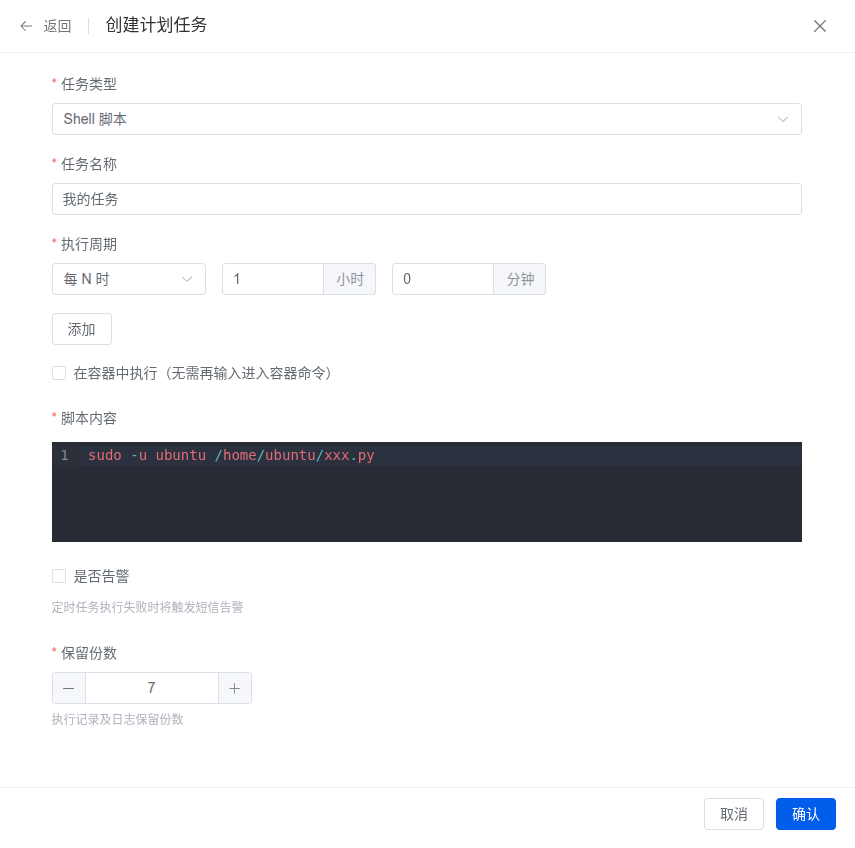
【Linux】使用1Panel 面板让服务器定时自动执行任务
服务器就是一台24小时开机的主机,相比自己家中不定时开关机的主机更适合完成定时任务,例如下载资源、备份上传,或者登录某个网站执行一些操作,只需要编写 脚本,然后让服务器定时来执行这个脚本就可以。 有很多方法实现…...

前端打包工具简单介绍
前端打包工具简单介绍 一、Webpack 架构与插件机制 1. Webpack 架构核心组成 Entry(入口) 指定应用的起点文件,比如 src/index.js。 Module(模块) Webpack 把项目当作模块图,模块可以是 JS、CSS、图片等…...
