Windows11安装及使用nvm
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
Windows11安装nvm
- 前言
- 一、简介
- 二、下载
- 三、安装
- 1、双击运行,同意协议,点击Next
- 2、选择nvm安装路径,此路径也是环境变量NVM_HOME的路径,点击Next
- 3、选择node安装目录,也是NVM_SYMLINK的路径,点击Next
- 4、点击Install
- 5、验证是否安装成功
- 6、配置下载镜像
- 四、使用
- 1、查看可以下载的node版本
- 2、下载
- 3、选择版本
- 1、查看当前版本和可选版本
- 2、选择需要的版本
- 3、验证node是否安装成功
- 五、常用命令
前言
一、简介
nvm 全称为 Node Version Manager,顾名思义就是用于管理多个 node.js 版本控制的工具。通过 nvm 可以安装和切换不同版本的 node.js。主要方便运行不同项目快速选择不同版本node.js。
二、下载
地址:https://github.com/coreybutler/nvm-windows/releases

三、安装
1、双击运行,同意协议,点击Next

2、选择nvm安装路径,此路径也是环境变量NVM_HOME的路径,点击Next

3、选择node安装目录,也是NVM_SYMLINK的路径,点击Next

4、点击Install

5、验证是否安装成功
nvm -v
出现版本号表示安装成功

6、配置下载镜像
在 nvm 的安装路径下,找到 settings.txt,在后面加上这两行,设置国内淘宝镜像源:
node_mirror: https://npmmirror.com/mirrors/node/
npm_mirror: https://npmmirror.com/mirrors/npm/
如下:

四、使用
1、查看可以下载的node版本
nvm ls available

2、下载
列表中显示的版本有限,可以访问:https://nodejs.org/download/release/ 找到你需要的版本,这里选择的是16.16.0版本。

nvm install 16.16.0

3、选择版本
1、查看当前版本和可选版本
nvm ls

2、选择需要的版本
nvm use 16.16.0

当前已经是16.16.0版本,如果有多个版本,本选中的前方有个符号 * 。

3、验证node是否安装成功
node -v
出现版本号,表示安装成功

五、常用命令
# 查看可下载版本
nvm ls available
# 安装指定版本
nvm install <version>
# 查看已下载版本
nvm ls
# 选择使用版本
nvm use <version>
# 卸载指定版本
nvm uninstall <version>
# 显示当前版本
nvm current
相关文章:

Windows11安装及使用nvm
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 Windows11安装nvm 前言一、简介二、下载三、安装1、双击运行,同意协议,点击Next2、选择nvm安装路径,此路径也是环境变量NVM_HOME的路径&am…...
机器学习 - 入门)
(一)机器学习 - 入门
数据集 数据集是一组数据的集合,这些数据可以是数值型、文本型、图形型等多种形式。数据集通常用于统计分析、机器学习、科学研究、商业智能等领域,以发现数据中的模式、趋势和关联性。 数据集的组成: 变量(Variables)…...

【解决】k8s使用kubeadm初始化集群失败问题整理
执行提示命令,查看报错信息 journalctl -xeu kubelet1、错误:running with swap on is no 报错 "command failed" err"failed to run Kubelet: running with swap on is no 解决: swap未禁用,需要禁用swap&…...

apache-dubbo
dubbo 文档地址 dubbo 官方文档地址 https://dubbo.apache.org/zh-cn/docs/user/references/api.html nacos 官方文档地址 https://nacos.io/zh-cn/docs/quick-start.html nacos下载地址 https://github.com/alibaba/nacos/releases/download/2.3.0/nacos-server-2.3.0.…...

ECharts柱状图-柱图2,附视频讲解与代码下载
引言: 在数据可视化的世界里,ECharts凭借其丰富的图表类型和强大的配置能力,成为了众多开发者的首选。今天,我将带大家一起实现一个柱状图图表,通过该图表我们可以直观地展示和分析数据。此外,我还将提供…...

【新人系列】Python 入门(十六):正则表达式
✍ 个人博客:https://blog.csdn.net/Newin2020?typeblog 📝 专栏地址:https://blog.csdn.net/newin2020/category_12801353.html 📣 专栏定位:为 0 基础刚入门 Python 的小伙伴提供详细的讲解,也欢迎大佬们…...

HTML综合
一.HTML的初始结构 <!DOCTYPE html> <html lang"en"><head><!-- 设置文本字符 --><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><!-- 设置网页…...

孚盟云 MailAjax.ashx SQL注入漏洞复现
0x01 产品简介 上海孚盟软件有限公司是一家外贸SaaS服务提供商,也是专业的外贸行业解决方案专业提供商。 全新的孚盟云产品,让用户可以用云模式实现信息化管理,让用户的异地办公更加流畅,大大降低中小企业在信息化上成本,用最小的投入享受大型企业级别的信息化服务,主要…...

解决“VMware虚拟机报Intel VT-x”错误
今天,在windows系统上,打开VMware WorkStation v15软件里的虚拟机,弹出"Intel VT-x处于禁用状态"错误,如图(1)所示: 图(1) 虚拟机报"Intel VT-x"错误 问题原因:当前电脑的BIOS没有开启…...

NiceGUI `ui.table` 基础
NiceGUI ui.table 基础 ui.table 是 NiceGUI 提供的一个组件,用于在页面上展示数据表格 基本概念 官方简介 A table based on Quasar’s QTable component. 参数参考rows:list of row objects; 行对象列表columns:list of column objects (defaults to the colu…...

分布式 Raft算法 总结
前言 相关系列 《分布式 & 目录》《分布式 & Raft算法 & 总结》《分布式 & Raft算法 & 问题》 参考文献 《Raft一致性算法论文译文》《深入剖析共识性算法 Raft》 简介 Raft 木筏是一种基于日志复制实现的分布式容错&一致性算法。在Raft算法…...

C++ 中面向对象编程如何实现动态绑定?
在 C 中,动态绑定(Dynamic Binding)是通过 虚函数(virtual function) 和 多态性(polymorphism) 来实现的。这是面向对象编程的重要特性之一,它允许程序在运行时根据对象的实际类型调…...

微服务-01
1.认识微服务 1.1 单体架构 单体架构(monolithic structure):顾名思义,整个项目中所有功能模块都在一个工程中开发;项目部署时需要对所有模块一起编译、打包;项目的架构设计、开发模式都非常简单。 当项目…...

这是一个vue3 + scss的数字滚动效果
介绍: 当数字变化时,只改变变化的数字位,其余的不变,可以递增、递减、骤变、负数也可以,但是样式要根据具体的项目需求去改; 效果1、增加数字: 效果2、减少数字: 使用方法: <te…...

数字证书管理工具 openssl keytool
OPENSSL 命令 openssl command [ command_opts ] [ command_args ] 常用command: version 用于查看版本信息 enc 用于加解密 ciphers 列出加密套件 genrsa 用于生成私钥 -des|-des3|-idea:用来加密私钥文件的三种对称加密算法。 rsa …...

Polars数据聚合与旋转实战教程
在这篇博文中,我们的目标是解决数据爱好者提出的一个常见问题:如何有效地从Polars DataFrame中创建汇总视图,以便在不同时间段或类别之间轻松进行比较。我们将使用一个实际的数据集示例来探索实现这一目标的各种方法。 Polars简介 Polars 是…...
)
引用类型集合的深拷贝,无需手动写循环:Apache Commons Lang (SerializationUtils)
在java中,我们如果想要对引用类型的集合进行深拷贝。有一种方式,就是调用SerializationUtils Apache Commons Lang (SerializationUtils) Apache Commons Lang 提供了 SerializationUtils 类,可以利用 Java 的序列化机制来进行集合及其元素…...

HTML、CSS表格的斜表头样式设置title 画对角线
我里面有用到layui框架的影响,实际根据你自己的框架来小调下就可以 效果如下 上代码 <!DOCTYPE html> <html lang"zh"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-wi…...

docker 安装mysql 5.7 详细保姆级教程
1. 安装mysql(5.7) docker pull mysql:5.7 若是拉取不了,可以配置下 docker 源 2. 查看是否安装成功 docker images 下图就是成功了 3.创建mysql专用目录、数据挂载目录、配置文件目录 ,演示目录在于/home/下 //命令逐条执行cd /home/ mkdir mysql …...

Kioptrix level3
声明! 学习视频来自B站up主 **泷羽sec** 有兴趣的师傅可以关注一下,如涉及侵权马上删除文章,笔记只是方便各位师傅的学习和探讨,文章所提到的网站以及内容,只做学习交流,其他均与本人以及泷羽sec团队无关&a…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...

02.运算符
目录 什么是运算符 算术运算符 1.基本四则运算符 2.增量运算符 3.自增/自减运算符 关系运算符 逻辑运算符 &&:逻辑与 ||:逻辑或 !:逻辑非 短路求值 位运算符 按位与&: 按位或 | 按位取反~ …...

【1】跨越技术栈鸿沟:字节跳动开源TRAE AI编程IDE的实战体验
2024年初,人工智能编程工具领域发生了一次静默的变革。当字节跳动宣布退出其TRAE项目(一款融合大型语言模型能力的云端AI编程IDE)时,技术社区曾短暂叹息。然而这一退场并非终点——通过开源社区的接力,TRAE在WayToAGI等…...

C/Python/Go示例 | Socket Programing与RPC
Socket Programming介绍 Computer networking这个领域围绕着两台电脑或者同一台电脑内的不同进程之间的数据传输和信息交流,会涉及到许多有意思的话题,诸如怎么确保对方能收到信息,怎么应对数据丢失、被污染或者顺序混乱,怎么提高…...
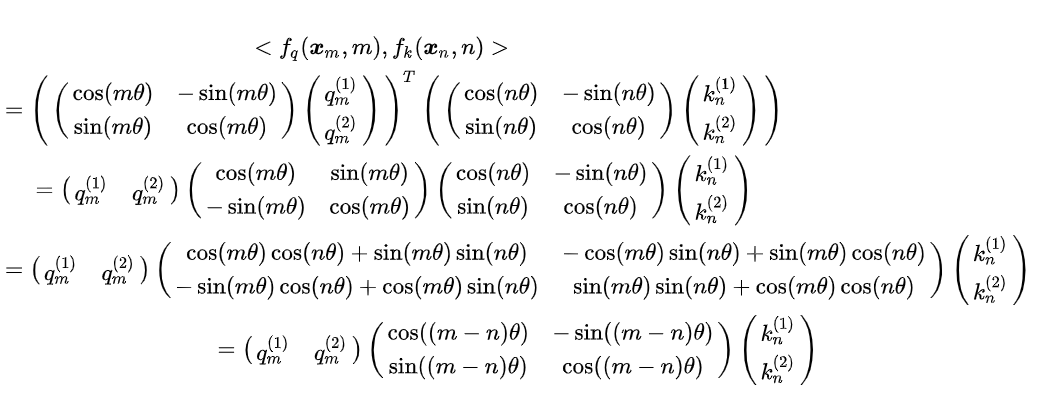
多模态学习路线(2)——DL基础系列
目录 前言 一、归一化 1. Layer Normalization (LN) 2. Batch Normalization (BN) 3. Instance Normalization (IN) 4. Group Normalization (GN) 5. Root Mean Square Normalization(RMSNorm) 二、激活函数 1. Sigmoid激活函数(二分类&…...

旋量理论:刚体运动的几何描述与机器人应用
旋量理论为描述刚体在三维空间中的运动提供了强大而优雅的数学框架。与传统的欧拉角或方向余弦矩阵相比,旋量理论通过螺旋运动的概念统一了旋转和平移,在机器人学、计算机图形学和多体动力学领域具有显著优势。这种描述不仅几何直观,而且计算…...
